药型罩材料性能参数对双模毁伤元成型的影响
2017-05-07樊雪飞李伟兵王晓鸣李军宝王雅君
樊雪飞, 李伟兵, 王晓鸣, 李军宝, 王雅君
(南京理工大学智能弹药技术国防重点学科实验室, 江苏 南京 210094)
1 引 言
药型罩作为聚能装药战斗部的关键部件,除结构参数外,药型罩材料性能对其毁伤元成型的影响也至关重要。如Ouye和Boeka等[1]研究发现药型罩材料强度对毁伤元头部速度具有重要影响; Rolc和Buchar等[2]研究了药型罩材料对EFP速度的影响,得出铁药型罩形成的侵彻体速度最高而钨材料的最小; Miller和 Kliminz[3]试验仿真研究发现高密度药型罩材料在小厚度、低强度时比大厚度和高强度时对不稳定性更加敏感,而低密度材料对不稳定性具有免疫性。随着材料特性研究的深入,更多金属材料被应用于药型罩。贺海民等[4]建立了不同炸药、不同起爆方式下钼药型罩战斗部模型,研究了钼药型罩杆式射流的成型过程; Fong和Ng等[5]应用钽粉末材料药型罩形成了爆炸成型侵彻体,得到了长杆状EFP毁伤元,验证了钽作为药型罩材料的可行性。王铁福等[6]仿真试验研究了药型罩材料的晶粒度对射流成型性能的影响规律。但是药型罩材料性能参数较多,各参数在材料变化后会产生交叉影响,因此,有必要研究单一材料各特征参数对毁伤元成型的影响,为今后药型罩材料的进一步拓展提供参考。Johnson-Cook本构模型综合反映了材料的塑性流变行为与应变率效应、温度效应和应变强化效应间的关系,且形式简单,使用方便,广泛应用于金属材料在大应变、高应变率及高温条件下的塑性变形行为的描述。
为此,本研究采用Johnson-Cook本构模型分析某成型装药结构(可形成爆炸成型弹丸(EFP)和聚能杆式侵彻体(JPC)双模毁伤元)材料性能参数对双模毁伤元成型的影响规律,并通过拟合影响规律曲线建立考虑材料性能影响的双模毁伤元头部速度及长径比计算公式。最后,对多种材料药型罩形成的双模毁伤元进行了X光成像验证试验。
2 单一材料特征参数对双模毁伤元成型的影响
2.1 计算模型及研究方案
前期针对装药及药型罩结构参数的影响开展了相关研究[7],确定了毁伤元成型较好时的装药及药型罩结构参数,装药结构及有限元模型如图1所示,主要包括药型罩、壳体和炸药。其中药型罩设计为弧锥结合形,装药口径Dk为100 mm,装药高度H为90 mm,船尾倾角β为45°,壳体壁厚t为5 mm。研究药型罩材料参数变化对双模毁伤元成形影响时,固定装药及药型罩结构,通过装药中点O处点起爆形成EFP毁伤元,装药斜坡A处六点环形起爆形成JPC毁伤元。
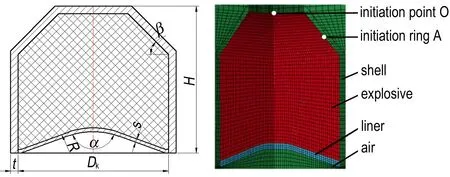
a. stern charge structure b. simulation model
图1 装药结构及有限元模型[7]
Fig.1 Charge structure and finite element model
紫铜的加工工艺较成熟,其密度、熔点等材料参数适中,能形成较佳的破甲毁伤元,是聚能装药战斗部最常用的药型罩材料。本课题组已基于紫铜材料优化设计了双模毁伤元成型较好的装药结构[7],因此本研究以紫铜材料参数为基础,研究单一材料特征参数变化对双模毁伤元成型的影响规律。
聚能装药毁伤元的形成过程具有高温、高应变率和高过载的特点,本研究采用ALE算法进行计算,炸药、药型罩、空气采用多物质欧拉算法,而炸药、药型罩、空气和壳体间的相互作用采用流固耦合算法。其中药型罩和壳体(45钢)本构方程选用Johnson-Cook本构模型,主装药为8701炸药,状态方程选为JWL(Jones-Wilkins-Lee)状态方程[7]。
Johnson-Cook本构方程中主要涉及准静态下屈服应力A、应变硬化系数B、应变率相关系数C、温度相关系数m、应变硬化指数n五个参数,每个模型参数取值的改变都会对毁伤元的成型指标产生重要影响。Johnson-Cook本构方程式为[8]:

首先基于紫铜确定仿真模型中各特征参数取初始值:A=90 MPa,B=292 MPa,C=0.025,n=0.31,m=1.09,ρ=8.96 g·cm-3。然后采用控制变量法,保持其余参数取值不变(即初始取值)对单一变量进行取值。各参数的取值变化范围按照几种典型药型罩材料所对应的参数取值范围取:ρ: 3~17 g·cm-3,A: 90~1640 MPa,B: 170~500 MPa,n: 0.08~0.4,C: 0.008~0.074,m: 0.45~1.35,各参数增量分别为:ρ: 2 g·cm-3,A: 100 MPa,B: 30 MPa,n: 0.04,C: 0.006,m: 0.05。仿真计算得到各参数在不同取值下EFP(200 μs)和JPC(150 μs)毁伤元头部速度和长径比,获得影响关系曲线,分析结果并找出规律。
2.2 屈服应力A的影响
采用数值仿真手段计算准静态下屈服应力A在90~1640 MPa范围内取值时EFP、JPC毁伤元的成型指标,得出头部速度和长径比随A变化的曲线如图2所示。

a. changing curves of vtip

b. changing curves of L/D
图2 EFP和JPC毁伤元的头部速度和长径比随准静态下屈服应力A的变化曲线
Fig.2 Changing curves of the tip velocity and length-diameter ratio of damage elements, EFP and JPC along with yield stressAunder quasi-state
从图2可以看出,随屈服应力A的增加,EFP和JPC毁伤元头部速度均呈现指数减小趋势,EFP长径比呈指数减小趋势,JPC长径比呈线性减小趋势。为保证最终各曲线可进行线性叠加,对图中的变化规律曲线进行指数拟合,得到速度和长径比表达式为:
EFP:
vEtip=154.34e(-A/507.8)+2319.67
L/DE=0.47105e(-A/937.62)+1.04708e(-A/179.1)+0.64173
式中,vEtip为EFP毁伤元头部速度,m·s-1;L/DE为EFP毁伤元长径比,下同。头部速度变化规律拟合方程相关系数R1=0.98054,长径比变化规律拟合方程相关系数R2=0.9875。
JPC:
vJtip=184e(-A/129.92)+382.72e(-A/1891.73)+2977.21
L/DJ=14.44e(-A/5623.56)-8.89
式中,vJtip为JPC毁伤元头部速度,m·s-1;L/DJ为JPC毁伤元长径比,下同。头部速度变化规律拟合方程相关系数R1=0.99886,长径比变化规律拟合方程相关系数R2=0.99089。
2.3 应变硬化系数B的影响
采用数值仿真手段计算应变硬化系数B在170~500 MPa内取值时EFP、JPC毁伤元的成型指标,得出头部速度和长径比随B的变化曲线,如图3所示。
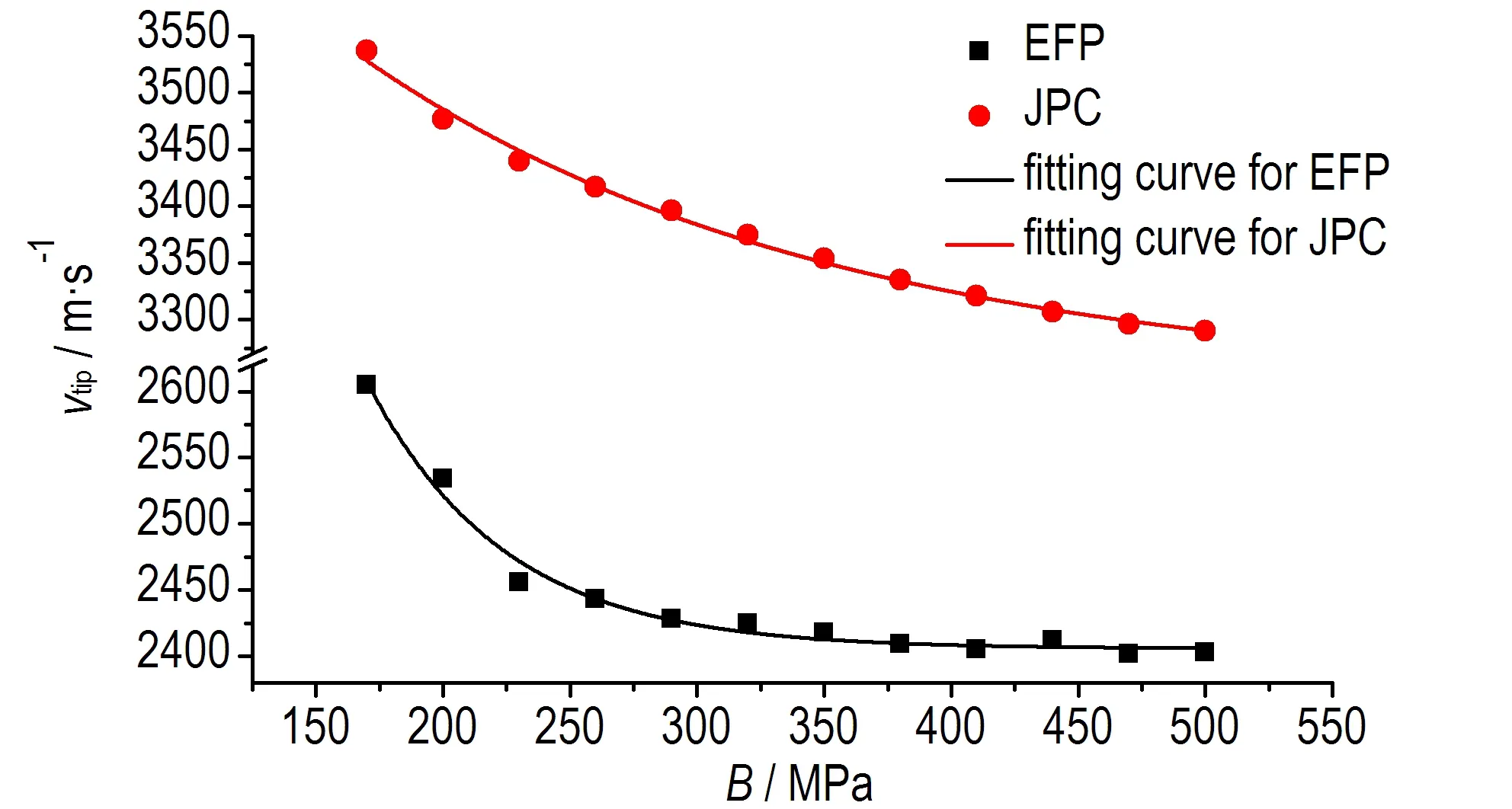
a. changing curves of vtip
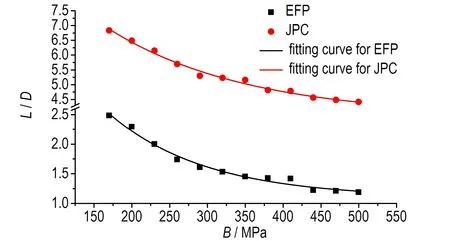
b. changing curves of L/D
图3 EFP、JPC毁伤元的头部速度和长径比随应变硬化系数B的变化曲线
Fig.3 Changing curves of the tip velocity and length-diameter ratio of damage elements, EFP and JPC along with strain hardening coefficientB
从图3可以看出,随着应变硬化系数B的增加,EFP及JPC毁伤元头部速度和长径比均呈现指数减小趋势,对图中的变化规律曲线进行指数拟合,得到速度和长径比表达式为:
EFP:
vEtip=4828.06e(-B/53.559)+2405.8
L/DE=5.32744e(-B/128.5489)+1.09757
式中,头部速度变化规律拟合方程相关系数R1=0.97939,长径比变化规律拟合方程相关系数R2=0.97774。
JPC:
vJtip=717.3e(-B/184.45)+3242.82
L/DJ=7.48e(-B/184.1)+3.92
式中,头部速度变化规律拟合方程相关系数R1=0.99273,长径比变化规律拟合方程相关系数R2=0.98518。
2.4 应变率相关系数C的影响
采用数值仿真手段计算应变率相关系数C在0.008~0.074范围内取值时EFP、JPC毁伤元的成型指标,得出头部速度和长径比随C的变化曲线,如图4所示。

a. changing curve of vtip
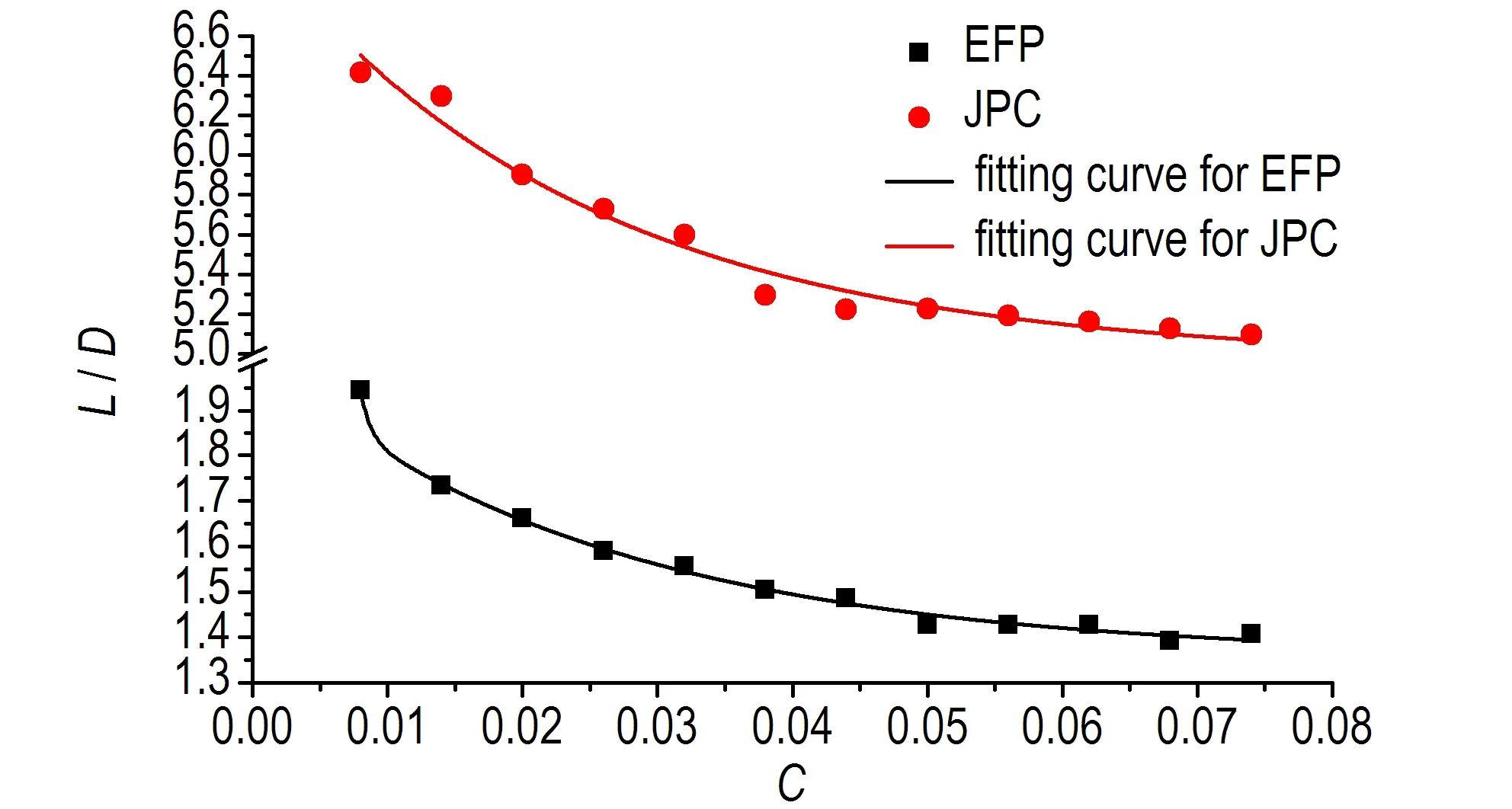
b. changing curve of L/D
图4 EFP、JPC毁伤元的头部速度和长径比随应变硬化指数C的变化曲线
Fig.4 Changing curves of the tip velocity and length-diameter ratio of damage elements, EFP and JPC along with strain hardening exponentC
从图4可以看出,随着应变率相关系数C的增加,EFP及JPC毁伤元头部速度和长径比均呈现指数减小趋势,对图中的变化规律曲线进行指数拟合,得到速度和长径比表达式为:
EFP:
vEtip=73.2e(-C/0.0273)+2397
L/DE=0.8221e(-C/0.0182)+1.3913
式中,头部速度变化规律拟合方程相关系数R1=0.97692,长径比变化规律拟合方程相关系数R2=0.99293。
JPC:
vJtip=53.62e(-C/0.0101)+2899.3e(-C/1.57)+562.5
L/DJ=2.134e(-C/0.024)+4.97
式中,头部速度变化规律拟合方程相关系数R1=0.99951,长径比变化规律拟合方程相关系数R2=0.9644。
2.5 温度相关系数m的影响
采用数值仿真手段计算温度相关系数m取值为0.45~1.35时,EFP、JPC毁伤元的成型指标,得出头部速度和长径比随m的变化曲线,如图5所示。

a. changing curves of vtip
b. changing curves of L/D
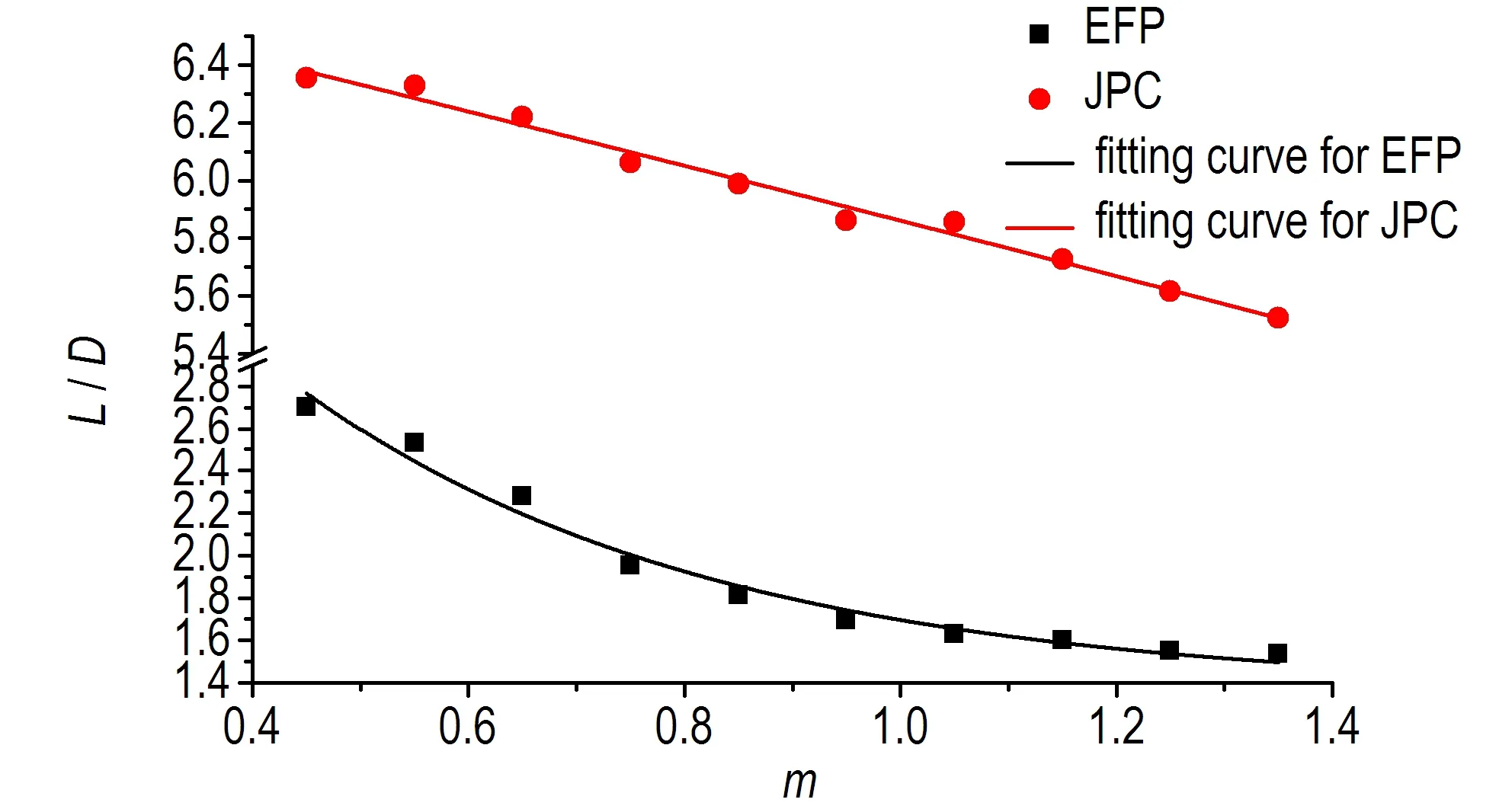
图5 EFP、JPC毁伤元的头部速度和长径比随温度相关系数m的变化曲线
Fig.5 Changing curves of the tip velocity and length-diameter ratio of damage elements, EFP and JPC along with temperature correlation coefficientm
从图5可以看出,随着温度相关系数m的增加,EFP毁伤元头部速度和长径比呈指数减小趋势,JPC毁伤元头部速度和长径比呈线性减小趋势。为保证最终各曲线可进行线性叠加,对图中的变化规律曲线进行指数拟合,得到速度和长径比表达式为:
EFP:
vEtip=1422.6e(-m/0.27396)+2399
L/DE=4.575e(-m/0.3806)+1.3654
式中,头部速度变化规律拟合方程相关系数R1=0.97751,长径比变化规律拟合方程相关系数R2=0.96928。
JPC:
vJtip=564.86e(-m/1.253)+3190.86
L/DJ=-15.53e(m/17.2)+22.32
式中,头部速度变化规律拟合方程相关系数R1=0.99491,长径比变化规律拟合方程相关系数R2=0.97832。
2.6 应变硬化指数n的影响
采用数值仿真手段计算应变硬化指数n在0.08~0.4范围内取值时EFP、JPC毁伤元的成型指标,得出头部速度和长径比随n变化的曲线,如图6所示。
a. changing curves of vtip

b. changing curves of L/D
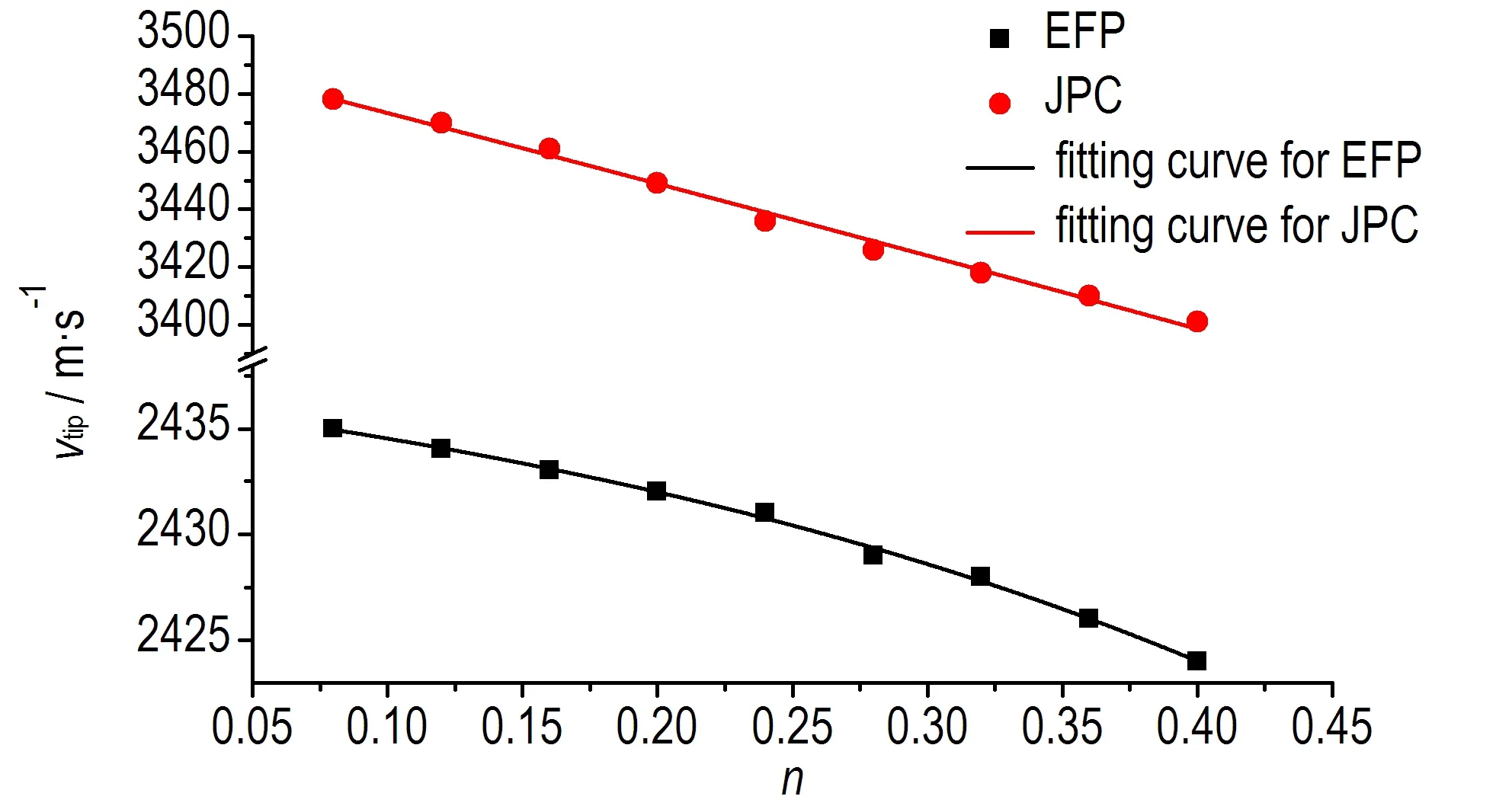
图6 EFP、JPC毁伤元的头部速度和长径比随应变应硬化指数n的变化曲线
Fig.6 Changing curves of the tip velocity and length-diameter ratio of damage elements, EFP and JPC along with strain hardening exponentn
从图6可以看出,随着应变硬化指数n的增加,EFP和JPC毁伤元长径比呈指数减小趋势,EFP头部速度呈指数减小趋势,JPC头部速度呈线性减小趋势,为保证最终各曲线可进行线性叠加,对图中的变化规律曲线进行指数拟合,得到速度和长径比表达式为:
EFP:
vEtip=-5.4e(n/0.336)+2441.78
L/DE=-0.1104e(n/0.3565)+1.89292
式中,头部速度变化规律拟合方程相关系数R1=0.99547,长径比变化规律拟合方程相关系数R2=0.98748。
JPC:
vJtip=-3182.28e(n/13)+6680.3
L/DJ=0.731e(-n/0.196)+5.42
式中,头部速度变化规律拟合方程相关系数R1=0.98883,长径比变化规律拟合方程相关系数R2=0.98007。
2.7 材料密度ρ的影响
采用数值仿真手段计算材料密度ρ取值为3~17 g·cm-3时EFP、JPC毁伤元的成型指标,得出头部速度和长径比随密度ρ的变化曲线,如图7所示。
a. changing curves of vtip
b. changing curves of L/D
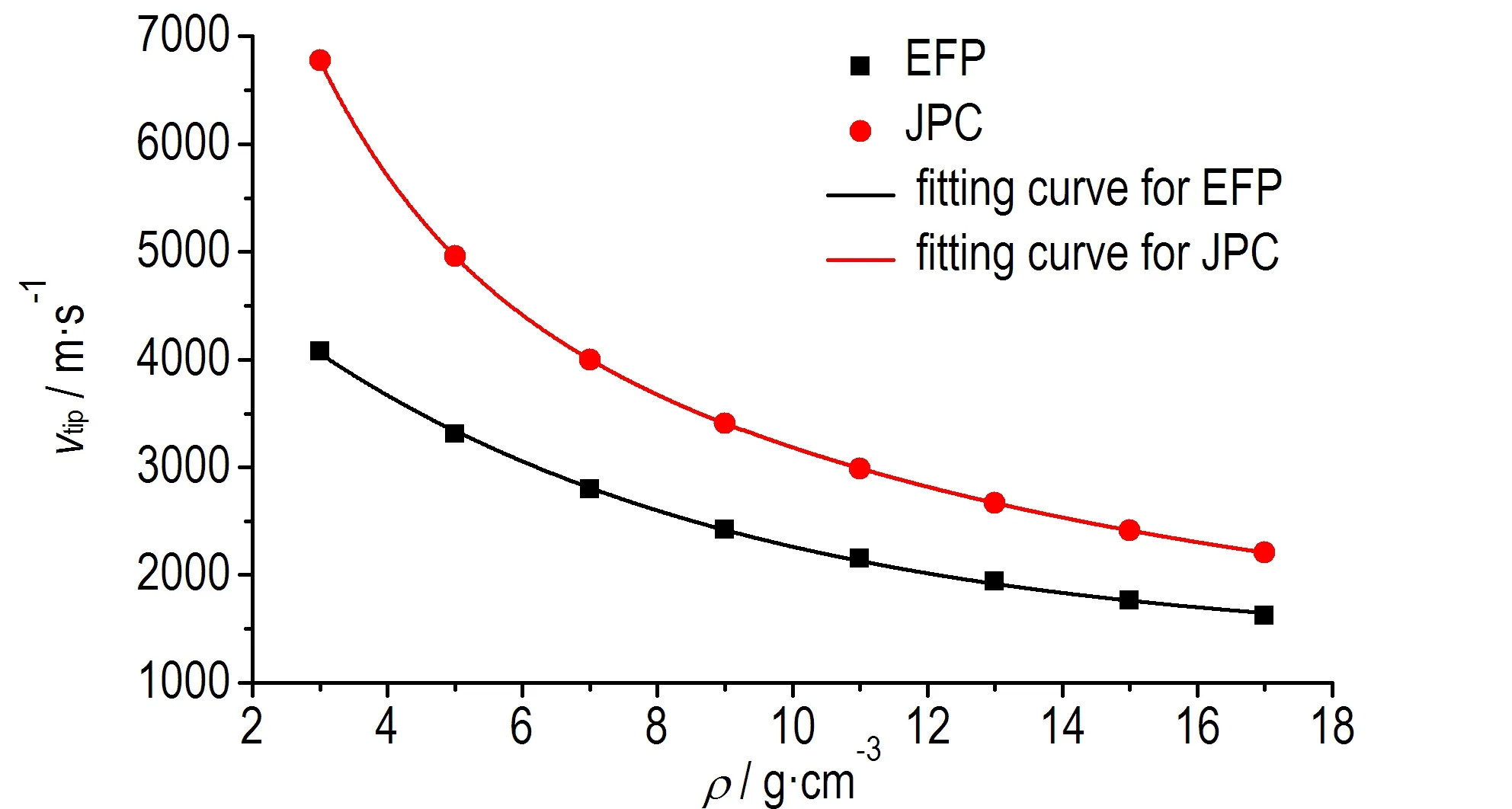
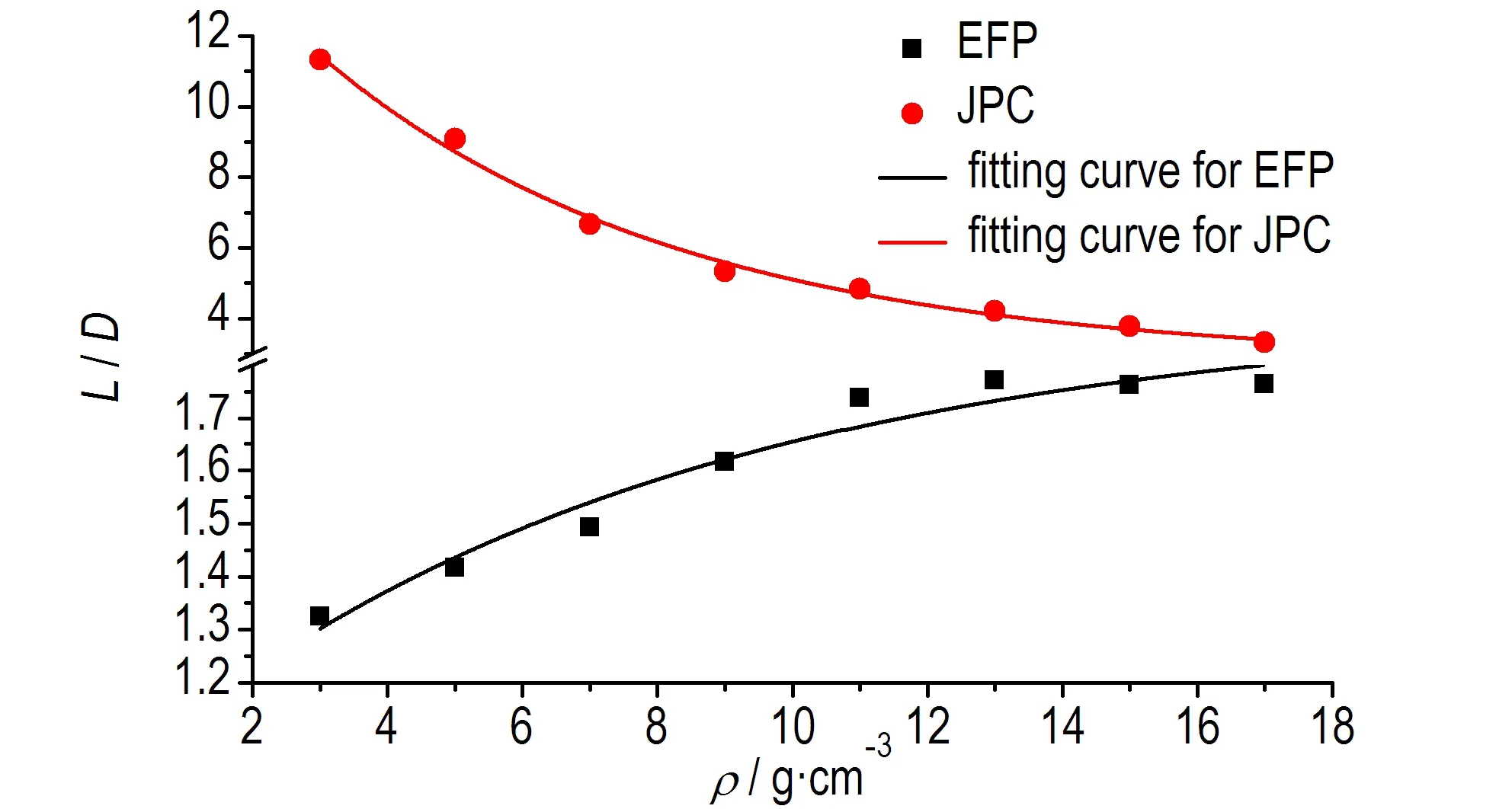
图7 EFP、JPC毁伤元的头部速度和长径比随密度ρ的变化曲线
Fig.7 Changing curves of the tip velocity and length-diameter ratio of damage elements, EFP and JPC along with densityρ
从图7可以看出,随着密度ρ的增加,EFP和JPC毁伤元头部速度呈指数减小趋势,EFP长径比呈指数增加趋势,JPC长径比呈指数减小趋势,对图中的变化规律曲线进行指数拟合,得到速度和长径比表达式为:
EFP:
vEtip=2899e(-ρ/3.69)+2732e(-ρ/19.39)+455
L/DE=-0.88e(-ρ/7.02)+1.9
式中,头部速度变化规律拟合方程相关系数R1=0.99863,长径比变化规律拟合方程相关系数R2=0.90521。
JPC:
vJtip=8406e(-ρ/1.914)+5038.3e(-ρ/9.95)+1292.94
L/DJ=15.24e(-ρ/5.3)+2.79
式中,头部速度变化规律拟合方程相关系数R1=1,长径比变化规律拟合方程相关系数R2=0.98795。
3 考虑材料性能影响的毁伤元成型参数计算公式
针对EFP毁伤元的成型计算主要采用经验公式、能量守恒法或动量守恒法计算其头部速度[9],对于JPC毁伤元的理论分析则主要通过PER理论[10],而传统的成型机理主要基于装药结构进行分析,未能考虑材料对于毁伤元成型的影响,使得计算不同材料药型罩成型过程时会有较大偏差。因此,有必要引入材料特性的影响来描述不同材料毁伤元成型之间的差异。
3.1 双模毁伤元头部速度计算分析
根据上文研究,应变硬化指数n的变化对EFP毁伤元的头部速度影响较小,因此摒弃参数n对EFP毁伤元头部速度的影响。各参数取值由最小值变到最大值时,EFP头部速度的变化率分别为:
A: 90~1506 MPa,
B: 177~426 MPa,
C: 0.008~0.06,
m: 0.55~1.09,
ρ: 2.77~17.6 g·cm-3,
针对EFP头部速度的各参数总的变化率为:
η=η1+η2+η3+η4+η5=81.4%
则各参数对于EFP头部速度影响的权重分别为:
ρ:η5/η=76.5%;A:η1/η=4.9%;
B:η2/η=8.4%;C:η3/η=2.3%;
m:η4/η=7.9%
分析各参数的权重值,密度对EFP速度的影响最大,由于在计算各参数对EFP头部速度的影响规律时基于铜的密度进行的计算,因此需要消除密度偏差给EFP头部速度带来的影响,引入密度修正系数K:
式中,ρCu和ρ分别为铜和所选材料的密度,g·cm-3。
由于各参数对EFP头部速度影响表达式均为指数形式,因此将各参数影响的表达式进行线性叠加后化简可得由材料特征参数表达的EFP毁伤元的头部速度表达式:
VEtip= 2218e(-ρ/3.7)+2090e(-ρ/19.4)+348+
K[7.6e(-A/508)+405.6e(-B/53.6)+1.7e(-C/0.03)+
112.4e(-m/0.3)+560]
同理,各参数对于JPC头部速度影响的权重分别为:
ρ:η5/η=76.7%;A:η1/η=9.2%;
B:η2/η=6.4%;C:η3/η=3.7%;
m:η4/η=4%
得到JPC毁伤元的头部速度表达式:
VJtip= 6447e(-ρ/1.9)+3864e(-ρ/9.95)+992+
K[16.9e(-A/130)+35.2e(-A/1892)+46e(-B/184)+
107e(-C/1.6)+22.6(-m/1.25)+630]
3.2 双模毁伤元长径比计算分析
准静态下屈服应力A和应变硬化系数B的变化对于EFP毁伤元长径比影响较大,n的变化对EFP毁伤元的长径比影响较小,因此摒弃参数n对EFP毁伤元长径比的影响。各参数取值由最小值变到最大值时,EFP长径比的变化率分别为:
A: 90~1506 MPa,
B: 177~426 MPa,
C: 0.008~0.06,
m: 0.55~1.09,
ρ: 2.77~17.6 g·cm-3,
针对EFP长径比的各参数总的变化率为:
ζ=ζ1+ζ2+ζ3+ζ4+ζ5=191.68%
则各参数对于EFP长径比影响的权重分别为:
ρ:ζ5/ξ=14.7%;A:ζ1/ξ=29.4%;B:ζ2/ξ=24.8%;
C:ζ3/ξ=13.6%;m:ζ4/ξ=17.5%
由于各参数的变化规律基于铜的参数进行的计算,为了消除铜的A、B取值偏差给EFP长径比带来的影响,引入修正系数K1、K2、K3:
式中,ACu为紫铜的屈服应力,MPa;A为所选材料的准静态下屈服应力,MPa;BCu为紫铜的应变硬化系数,B为所选材料的应变硬化系数。
因为A和B为同量纲量,因此可对A和B进行线性相加,则K3的表达式为:
由于各参数对EFP长径比影响表达式均为指数形式,因此将各参数影响的表达式进行线性叠加后化简可得由材料特征参数表达的EFP毁伤元的长径比表达式:
L/DE=K2[0.138e(-A/938)+0.308e(-A/179)+0.189]+
K1[1.321e(-B/128)+0.272]+K3[0.112e(-C/0.02)+
0.8e(-m/0.38)-0.129e(-ρ/7.02)+0.707]
同理,得到各参数对于JPC长径比影响的权重分别为:
ρ:ζ5/ξ=37.5%;A:ζ1/ξ=31%;B:ζ2/ξ=16.4%;
C:ζ3/ξ=10.9%;m:ζ4/ξ=4.2%
得到JPC毁伤元的长径比表达式:
L/DJ= 5.715e(-ρ/5.3)+1.05+
K[4.476e(-A/5624)+1.23e(-B/184)+
0.23e(-C/0.024)-0.652e(m/17.2)-0.634]
4 不同材料双模毁伤元成型参数计算试验验证
4.1 不同材料双模毁伤元X光成像测试结果
根据图1所示的成型装药结构及如表1仿真所采用的材料模型参数[11],分别加工铝、铁、铜三种药型罩材料的成型装药试验装置,进行X光成像试验,试验获得X光照片与仿真结果对比见表2。
表1 仿真所采用的材料模型参数
Table 1 The model parameters of materials used in simulation
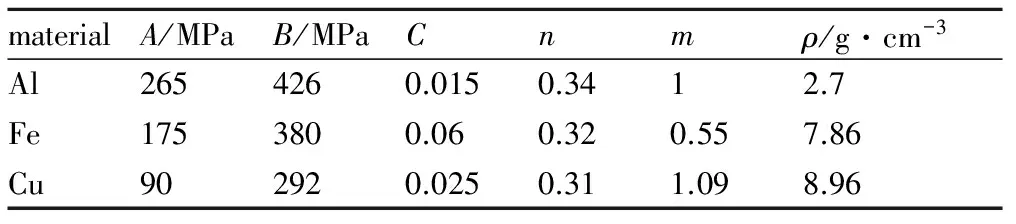
materialA/MPaB/MPaCnmρ/g·cm-3Al2654260.0150.3412.7Fe1753800.060.320.557.86Cu902920.0250.311.098.96
从表2可以看出,三种材料双模毁伤元成型仿真计算结果与试验测试结果吻合较好,因此可用该有限元模型描述不同材料双模毁伤元成型之间的差异,紫铜无论是EFP还是JPC毁伤元拉伸效果最好,铁次之,铝由于熔点过低导致了JPC毁伤元发生了严重的气化断裂现象。
4.2 理论、仿真与试验对比
按照3.1和3.2节拟合的计算模型公式分别对铝、铁、铜进行计算,所得计算结果与仿真和试验结果见表3。
由表3可知,铝、铁、铜三种材料形成EFP毁伤元头部速度的计算结果与试验之间的误差分别为2.7%、8.5%、5.1%,长径比数值的误差分别为7.4%、9.8%、7.8%; JPC毁伤元头部速度计算结果与试验之间的误差分别为3.2%、6.1%、6.0%,长径比结果的误差分别为6.7%、6.2%、6.5%。采用本文拟合计算结果与试验结果之间误差小于10%,故拟合得出的考虑材料性能的毁伤元计算公式的精度较高,可用于计算该装药结构下不同材料药型罩形成EFP、JPC毁伤元时的头部速度和长径比。
表2 不同材料EFP、JPC毁伤元的试验及仿真结果
Table 2 The experimental and simulating results of damage elements, EFP and JPC for different materials

materialAlFeCuEFPX⁃raysimulationJPCX⁃raysimulation
表3 仿真、计算、试验结果的对比
Table 3 Comparison of the results obtained by simulation, calculation and experiment

materialdamageelementssimulationvtipL/DcalculationvtipL/DexperimentvtipL/DAlEFP45220.86250530.76149200.705JPC742115.740795214.739769613.755FeEFP25911.09226731.08724460.980JPC35034.93537494.86335224.564CuEFP24271.66924331.65523091.796JPC34205.66034155.44932065.826
5 结 论
(1)该种装药结构下,双模毁伤元EFP和JPC的头部速度和长径比随准静态下屈服应力A、硬化系数B、应变硬化指数C、温度相关系数m、应变硬化指数n取值的增加均呈现指数递减规律; 而随着特征参数密度ρ的增加,EFP头部速度呈指数减小趋势,长径比呈指数增加趋势,JPC毁伤元头部速度和长径比都成指数减小趋势变化。
(2)针对双模毁伤元的成型,密度ρ对EFP和JPC毁伤元的头部速度影响最大,准静态下屈服应力A和应变硬化系数B对EFP毁伤元长径比影响最大,密度ρ和准静态下屈服应力A对JPC毁伤元长径比影响最大。
(3)建立了考虑材料性能影响的双模毁伤元成型参数头部速度和长径比的计算公式,并进行了不同材料的X光成像试验验证,试验结果与仿真及计算结果较吻合,公式计算与试验结果误差控制在小于10%,该计算公式可较好地预测毁伤元成型参数。
参考文献:
[1]Ouye N, Boeka D, Hancock S. Material strength effects on shaped charge tip velocities[C]∥Proceedings of the 23rd International symposium on ballistics, Tarragona, Spain. 2007:215-222.
[2]Rolc S, Buchar J, Akstein Z. Computer simulation of explosively formed projectiles (EFP) [C]∥Proceedings of the 23th international symposium on ballistics, Tarragona, Spain. 2007: 185-192.
[3]Miller S, Kliminz G. The role of Rayleigh Taylor instability in shaped charge jets formation and stability[C]∥Proceedings of the 22ndinternational symposium on ballistics, Vancouver, Canada. 2005:468-475.
[4]贺海民,王利侠,孙建,等. 钼药型罩杆状射流形成的数值模拟及实验研究[J]. 爆炸与冲击,2013(Suppl.): 28-33.
HE Hai-min, WANG Li-xia, SUN Jian et al. Experiment and numerical simulation on rod-like jet formation by molybdenum liner[J].ExplosionandShockWaves, 2013 (Suppl.): 28-33.
[5]Fong R, Ng W, Tang S, et al. Application of powder tantalum material for explosively formed penetrator[C]∥Proceedings of the 22ndInternational symposium on ballistics, Vancouver, Canada. 2005: 677-681.
[6]王铁福,王雷,阮文俊,等. 药型罩材料的晶粒度对射流性能的影响[J]. 高压物理学报,1996,10(4): 291-298.
WANG Tie-fu, WANG Lei, RUAN Wen-jun et al. A constitutive model and data for metals subjected to large strain, high strain rates and high temperature [J].ChineseJournalofHighPressurePhysics, 1996, 10(4): 291-298.
[7]Li Weibing, Wang Xiaoming, Li Wenbin. The effect of annular multi-point initiation on the formation and penetration of an explosively formed penetrator[J].InternationalJournalofImpactEngineering. 2010, 37(4): 414-424.
[8]Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]∥Proceedings of the 7th International symposium on ballistics, Hague, Netherlands. 1983:541-547.
[9]林加剑. EFP成型及其终点效应研究[D]. 合肥: 中国科学技术大学,2009.
LIN Jia-jian. Research on the formability of EFP and its terminal effect [D]. Hefei: University of Science and Technology of China, 2009.
[10]黄正祥. 聚能杆式侵彻体成型机理研究[D]. 南京: 南京理工大学,2003.HUANG Zheng-xiang. Mechanism study on jetting projectile charge formation [D]. Nanjing: Nanjing University of Science & Technology, 2003.
[11]Li W B, Li W B, Wang X M, et al. Effect of the liner material on the shape of dual mode penetrators [J].Combustion,ExplosionandShockWaves,2015, 51(3): 387-394.
