运输过程火箭战斗部装药振动疲劳的数值分析

张巍耀, 涂小珍, 蓝林刚, 董天宝

(中国工程物理研究院化工材料研究所含能材料测试与评价中心, 四川 绵阳 621999)

1 引 言

战斗部装药既是系统的主要功能部分也是承受载荷的结构件。当火箭在平整度较差的道路上运输时,路面激励会使弹体及内部装药发生显著的弹性振动,使其结构内部产生损伤、裂纹等。此类缺陷不仅会降低装药的结构可靠性,还会使热点显著增加进而降低其安全性[1-3]。因此,有必要研究路面激励下战斗部装药的振动特性及疲劳损伤情况。

目前,材料缺陷检测技术已得到深入发展,相关直接检测技术(CT、X光、超声等)和间接监测分析手段已能准确探明装药缺陷[4-7],但由于运输过程中装药通常封装在弹体内部,且路面载荷为随时间变化的非确定性随机激励,传统的检测、监测技术难以有效评估其疲劳损伤程度。工程上通常采用时域方法和频域方法研究构件在随机载荷下的振动特性及疲劳损伤情况。时域法主要有谐波叠加法、参数模型法和逆傅立叶变换法等[8-9]。由于时域方法在对随机过程进行仿真模拟时需要进行大量的数值运算,难以广泛应用于复杂系统的疲劳分析上。频域法由系统传递函数求出响应功率谱及概率密度分布,然后根据材料S-N曲线及累积损伤假设计算疲劳寿命期望。其不仅避免了繁重的计算量,且能充分表征系统的随机特性,是目前研究随机载荷作用下结构疲劳寿命的最有效方法。如贺光宗等[10]使用频域方法计算了多轴随机载荷下结构的疲劳寿命。方吉等[11]研究了焊接结构疲劳寿命的频域预测方法。Steinberg[12]基于高斯概率分布和Miner线性累积损伤理论提出了疲劳寿命预测的三区间法。该方法计算简单且可操作性强,已被广泛应用于机翼、车架等复杂结构的疲劳寿命评估[13-14]。近年来频域方法在复杂随机系统特别是非高斯随机过程疲劳寿命分析上得到了进一步发展[15-16]。

国内外研究人员针对火箭装药动态特性及疲劳寿命开展了相关研究。Eric Osborne[17]曾对飞行状态下火箭装药的振动特性进行了详细讨论。Yildirim等[18]使用数值模拟方法研究了装药在压力、温度载荷下的动态特性,给出了老化和损伤对结构响应的影响规律。李恩奇等[19]利用有限元方法研究了某火箭发动机药柱的随机振动特性。曲凯等[20-21]采用时域方法研究了舰载火箭推进剂药柱在摇摆载荷下的动态特性,并由雨流计数法和Miner线性累积损伤理论计算了装药的疲劳寿命。李记威等[22]使用相同的方法分析了某空空导弹药柱的挂飞振动疲劳寿命。然而目前关于装药在随机载荷下振动疲劳的研究报道并不多见。

本研究分析了路面随机激励下战斗部装药的振动特性并对疲劳损伤情况进行了评估。首先利用频域方法建立火箭发射车简化动力学模型,由路面激励及传递函数求出装药的随机振动响应; 然后通过结构危险点应力概率密度分布及Steinberg 3-σ法则对装药的疲劳损伤进行评估。

2 动力学模型

图1为火箭发射车示意图,仅考虑弹体在垂直运输方向上的结构振动,将其动力学模型简化为图2所示。其中车架和弹体等效为均质刚性梁,车轮悬架等效为阻尼器和弹簧,挂载点等效为弹簧。

图1 火箭发射车示意图

Fig.1 The rocket launcher

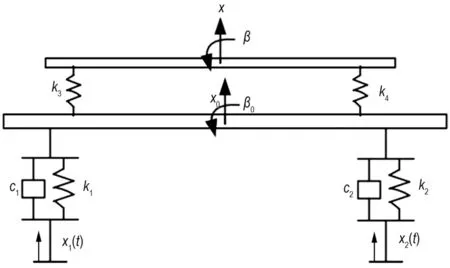
图2 发射车简化模型示意图

Fig.2 The simplified mechanical model of the rocket launcher

选取车架和弹体在垂直运输方向上的位移及对称面内的转角作为广义坐标,由第二类拉格朗日方程导出系统动力学控制方程[23]:

(1)

式中:

x0、β0、x和β分别为车架和弹体的质心位移和转角,m0和m分别为车架和弹体质量,l0和l分别为车架和弹体的等效长度,x1(t)和x2(t)为路面激励,c1和c2为车轮悬挂阻尼,k1和k2为车轮悬挂刚度,k3和k4为弹体支撑点刚度。对式(1)做傅里叶变换可得系统响应Z(w)对路面激励w(w)的传递函数:

(2)

进一步推导出弹体支撑点响应功率谱函数:

(3)

(4)

Sw为路面激励w(w)的自功率谱密度,

建立火箭简化有限元模型,如图3所示,以Sk3w和Sk4w作为激励,求得战斗部装药基础激励功率谱。

建立装药有限元模型,由基础激励谱密度计算结构随机振动响应。设P(S)为危险点应力响应峰值概率密度函数,满足正态分布规律,如图4所示。其中,响应幅值不超过1σ的概率为68.26%,不超过2σ的概率为95.44%,不超过3σ的概率为99.73%。

根据Miner线性累积损伤理论[12],随机系统的疲劳损伤期望为:

(5)

式中,λ为加载频率的数值期望,T为加载时间,N(S)为应力幅值为S时的疲劳极限。Steinberg在此基础上提出了更加简便的三区间法来预测结构的疲劳损伤情况[12]:

(6)

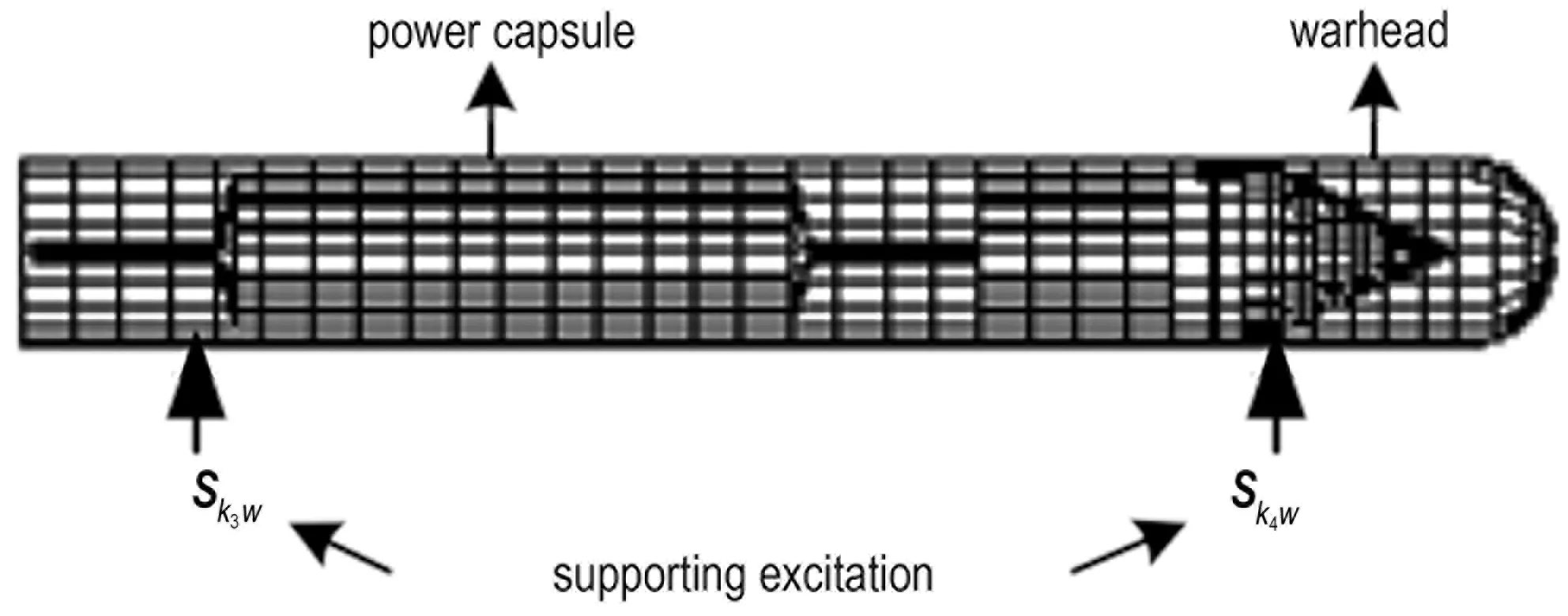
图3 火箭结构有限元模型

Fig.3 The rocket finite element model

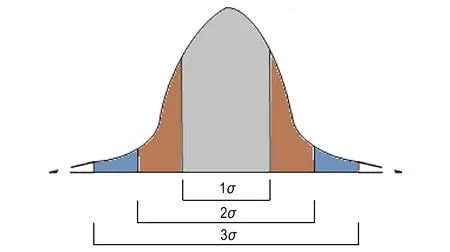
图4 随机响应高斯概率密度分布

Fig.4 Gaussian probability density distribution of the random dynamic response

3 算例分析

设战斗部装药材料为某高聚物粘结炸药,密度ρ=1847 kg·m-3,弹性模量E=10 GPa,泊松比μ=0.33。结构尺寸如图5a所示,其中壁厚为2 cm,顶部圆孔半径为1.5 cm。装药底部和顶部为固定约束边界条件,Y轴与弹体对称轴重合,X轴垂直于运输平面。图5b为ANSYS软件建立的装药结构有限元模型,单元类型为SOLID185六面体单元,单元平均尺寸为5 mm。图6为装药基础激励加速度功率谱密度曲线。

a. symmetry plane dimension b. three-dimensional finite element model

图5 装药结构示意图

Fig.5 The rocket warhead charge

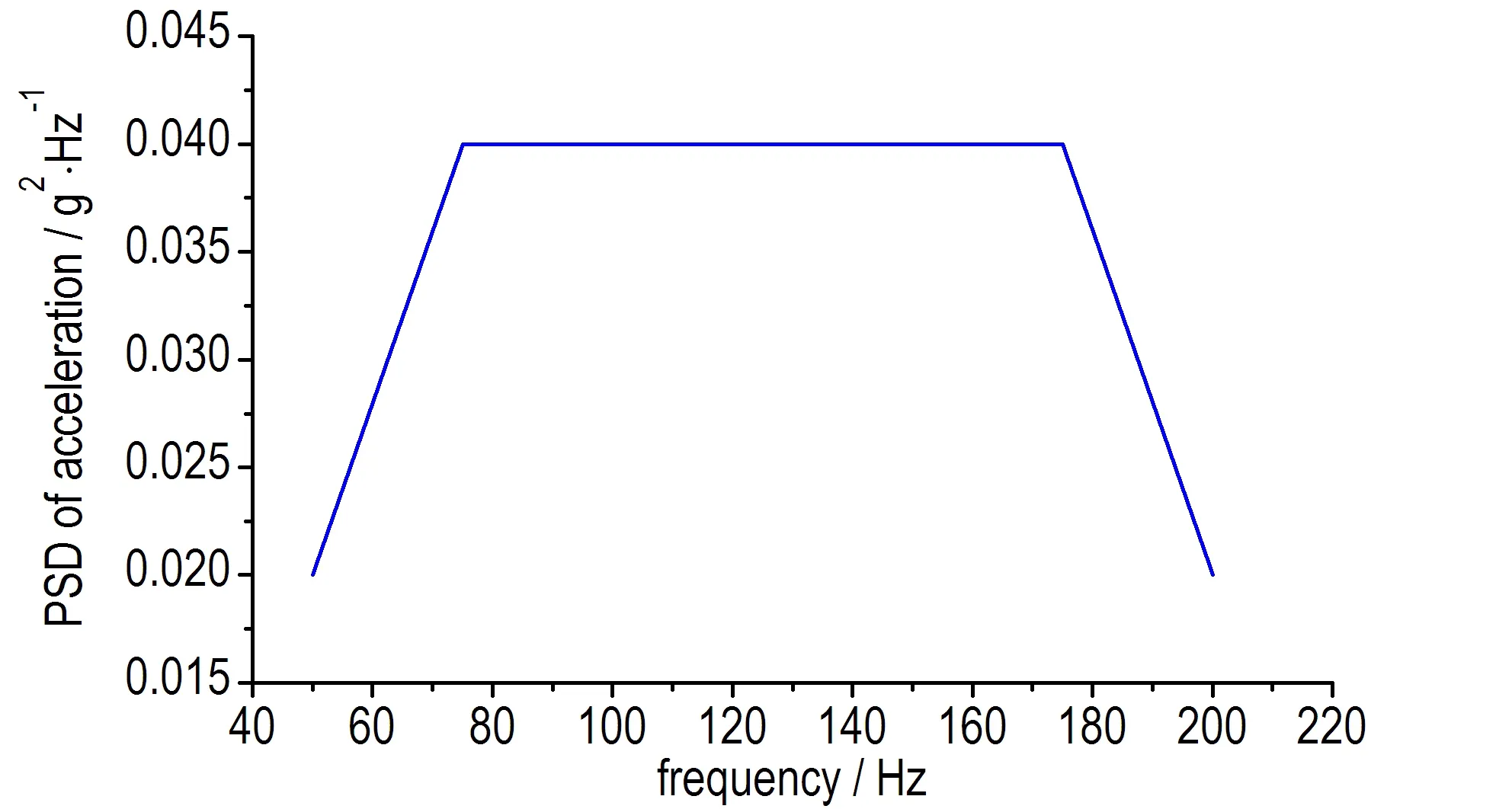
图6 装药基础激励加速度功率谱密度曲线

Fig.6 The acceleration PSD of the base excitation

对装药有限元模型进行模态计算,图7为其前4阶模态振型,图8为其前10阶固有频率。可以发现装药前3阶模态频率均处于基础激励频率范围内。这表明在路面随机激励作用下装药很可能会发生显著的结构振动。

截取有限元模型前10阶振型,采用模态叠加法计算结构随机振动响应,计算结果满足正态分布规律。图9为1σ概率条件下装药在垂直运输方向上的变形分布云图。可以发现装药与弹体连接部位的变形量最小,中间部位的变形量最大。1σ概率条件下的最大变形量为1.38×10-3mm。

图10为装药最大变形处的加速度功率谱密度曲线。可以发现在第二阶固有频率处加速度响应达到峰值。这是由于第二阶模态以X轴方向变形为主,振动方向与路面载荷平行,从而使装药的结构变形以第二阶模态变形为主。

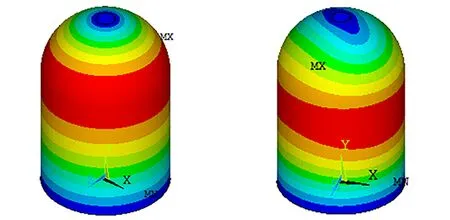
a. 1stmode with frequency b. 2ndmode with frequency of 142.3 Hz of 156.1 Hz

c. 3rdmode with frequency d. 4thmode with frequency >of 190.6 Hz of 227.7 Hz

图7 装药固有频率与振型

Fig.7 Mode frequencies and shapes of the charge

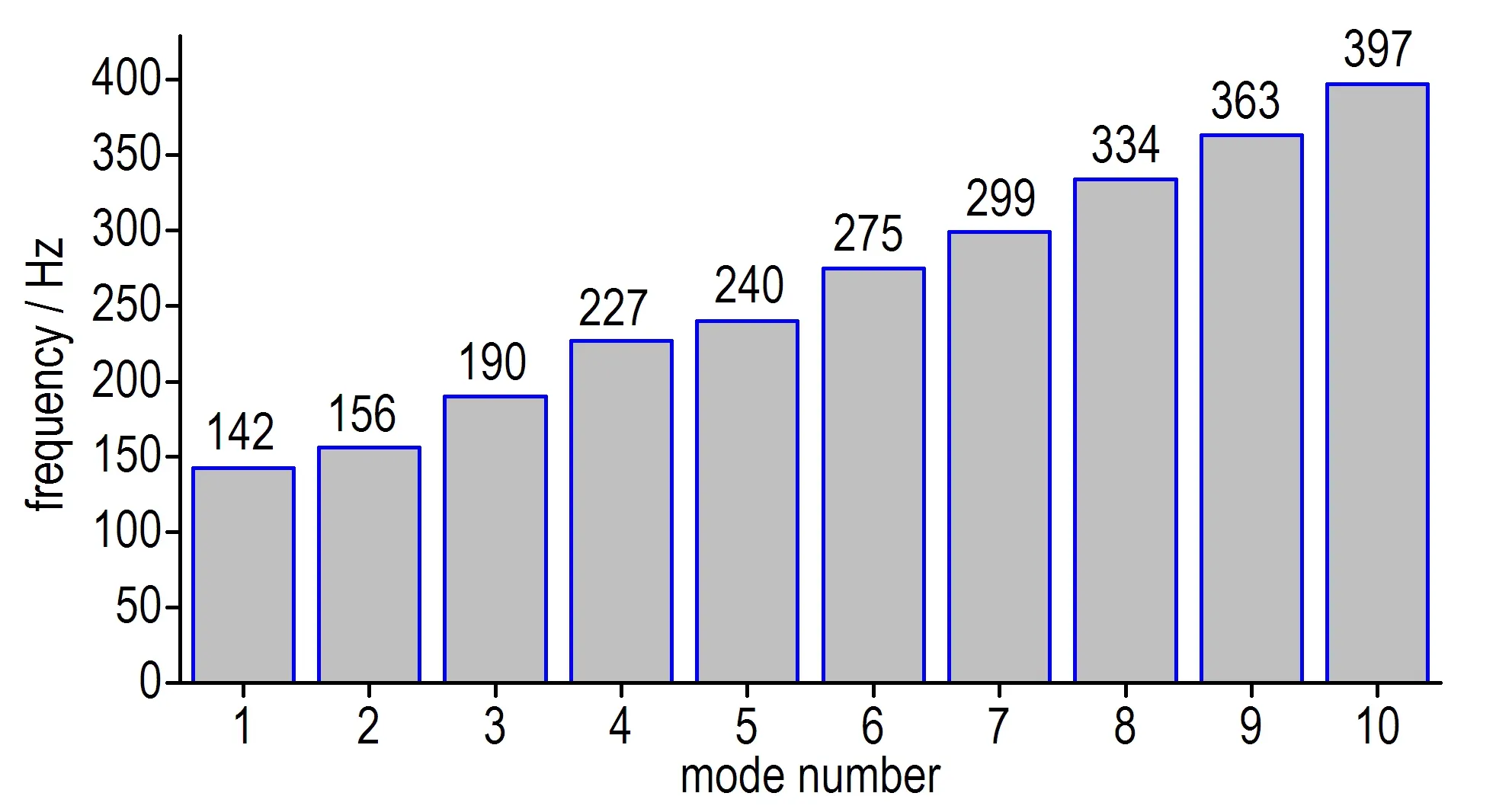
图8 装药固有频率

Fig.8 Mode frequencies of the charge

图9 装药X方向振动位移

Fig.9 Vibration displacement of the charge in theXdirection

图10 最大变形处加速度功率谱密度

Fig.10 The acceleration PSD of the point with the largest deformation

图11为装药第一等效主应力分布云图。可以发现最大应力位于装药顶部通孔内侧,此部位为结构危险点,即疲劳损伤的起始位置。危险点第一等效主应力值如表1所示。

图12为材料应力—寿命(S-N)曲线。由Steinberg三区间法计算装药疲劳损伤量,表2为不同加载时间下的疲劳损伤情况。

可以发现当加载时间为50 h和100 h时,损伤量均小于1,装药结构还未发生疲劳破坏。当加载时间为250 h时损伤量为1.12,装药已经发生结构破坏。

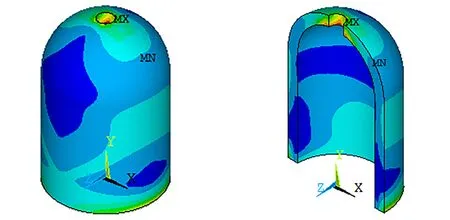
a. inner stress distribution b. inner stress distribution of the whole part of the cutting segment

图11 装药第一等效主应力分布

Fig.11 1stprincipal stress distribution of the charge

图12 单轴拉伸疲劳S-N曲线

Fig.12 Uniaxial tensionS-Ncurve of the charge material

表1 危险位置第一等效主应力

Table 1 1stprincipal stress values of the danger point

probabilitystressvalue/MPa0.6826(1σ)≤1.620.9544(2σ)≤3.240.9973(3σ)≤4.86

表2 装药疲劳损伤情况

Table 2 Fatigue damage degree of the charge at different moments

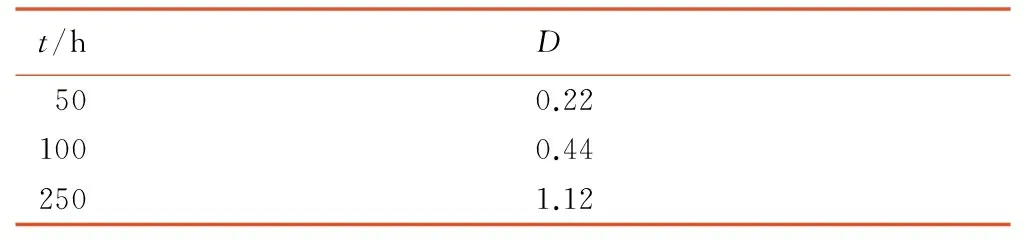
t/hD500.221000.442501.12

4 结 论

(1) 由于低阶模态处于基础激励频谱范围内,因此在路面随机激励作用下装药发生了显著的结构振动。

(2) 装药的随机振动使结构内部产生了显著的动应力,疲劳损伤由最大应力处即“危险点”开始,且随加载时间增长不断加剧。在250 h时累积损伤量达到1.12,装药已经发生结构破坏。

(3) 频域方法能有效分析战斗部装药在运输环境下的动态特性及损伤演化规律,可为其振动疲劳寿命及结构可靠性评估提供理论指导。

参考文献:

[1] Rashkovsky S A, Milyokhin Y M, Klyuchnikov A N, et al. Effect of tension of a composite propellant on its burning rate[J].CombustionExplosionandShockWaves, 2009, 45(6): 678-685.

[2] 高艳宾, 陈雄, 胡少青, 等. 疲劳损伤对NEPE推进剂力学性能的影响[J]. 弹箭与制导学报, 2014, 34(2): 90-93.

GAO Yan-bing, CHEN Xiong, HU Shao-qing, et al. The effect of fatigue damage on mechanical property of NEPE propellant[J].JournalofProjectilesRocketsMissilesandGuidance, 2014, 34(2): 90-93.

[3] 郑雪, 王娟, 于劭钧, 等. PBX细观损伤及其与安全性能的关系研究[J]. 材料保护, 2014, 47(S1): 166-171.

ZHENG Xue, WANG Juan, YU Shao-Jun, et al. Micro-damage in PBX and its influence on sensitivity[J].MaterialsProtection, 2014, 47(S1): 166-171.

[4] WANG Xian, MA Sao-peng, ZHAO Ying-tao, et al. Observation of damage evolution in polymer bonded explosives using acoustic emission and digital image correlation[J].PolymerTesting, 2011, 30(8): 861-866.

[5] LIU Rui, LI Ming, LI Jing-ming, et al. Modeling the damage evolution in compressed polymer bonded explosives based on computed micro tomography images[J].Science&TechnologyofEnergeticMaterials, 2013, 74(1): 29-33.

[6] LI Jun-Ling, FU Hua, TAN Duo-Wang, et al. Fracture behaviour investigation into a polymer-bonded explosive[J].strain, 2012, 48(6): 463-473.

[7] 刘佳辉, 刘世俊, 黄明, 等. 压制PBX中炸药晶体损伤的研究进展[J]. 含能材料, 2013, 21(3): 372-378.

LIU Jia-hui, LIU Shi-jun, HUANG Ming, et al. Progress on crystal damage in pressed polymer bonded explosives[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2013, 21(3): 372-378.

[8] Figwer J. A new method of random time-series simulation[J].SimulationPracticeandTheory, 1997, 5(3): 217-234.

[9] ZHANG Yong-lin, ZHANG Jia-fan. Numerical simulation of stochastic road process using white noise filtration[J].MechanicalSystemsandSignalProcessing, 2006, 20(2): 363-372.

[10] 贺光宗, 陈怀海, 贺旭东. 一种多轴向随机激励下结构疲劳寿命分析方法[J]. 振动与冲击, 2015, 34(7): 59-63.

HE Guang-zong, CHEN Huai-hai, HE Xu-dong. Vibration fatigue life prediction method for structures under multi-axial random excitations[J].JournalofVibrationandShock, 2015, 34(7): 59-63.

[11] 方吉 李季涛 王悦东, 等. 基于随机振动理论的焊接结构疲劳寿命概率预测方法研究[J]. 工程力学, 2016, 33(3): 24-30.

FANG Ji, LI Ji-tao, WANG Yue-dong, et al. Research on fatigue life probability prediction method of welded structure based on random vibration theory[J].EngineeringMechanics, 2016, 33(3): 24-30.

[12] 朱学旺, 张思箭, 宁佐贵, 等. 3σ准则应用对结构疲劳损伤评价的影响分析[J]. 航天器环境工程, 2014, 31(6): 609-613.

ZHU Xue-wang, ZHANG Si-jian, NING Zuo-gui, et al. Applications of 3σ clipping rule in the fatigue damage accumulation analysis[J].SpacecraftEnvironmentEngineering, 2014, 31(6): 609-613.

[13] 徐和林, 韩致信, 崔继强, 等. 7140型客车车架随机振动特性及疲劳强度分析[J]. 机械设计, 2012, 29(3): 7-10.

XU He-lin, HAN Zhi-xin, CUI Ji-qiang, et al. Analysis of random vibration and fatigue strength of 7140 bus frame[J].JournalofMachineDesign, 2012, 29(3): 7-10.

[14] 孟凡涛, 胡愉愉. 基于频域法的随机振动载荷下飞机结构疲劳分析[J]. 南京航空航天大学学报, 2012, 44(1): 32-36.

MENG Fan-tao, HU Yu-yu. Analysis of aircraft structural fatigue under random vibration loadings based on information in frequency domain[J].JournalofNanjingUniversityofAeronauticsandAstronautics, 2012, 44(1): 32-36.

[15] Rice S O. Mathematicalanalysis of random noise[J].BellSystemTechnicalJournal, 2015, 24(1): 146-156.

[16] Lu Peng-min, Zhao Bang-hua, Yan Jun-mao. Efficient algorithm for fatigue life calculations under broad band loading based on peak approximation[J].JournalofEngineeringMechanics, 2014, 124(2): 233-236.

[17] Osborne E. Solid rocket motor random vibration[C]∥Joint Propulsion Conference and Exhibit. 2001.

[18] Yildirim H C, Ozupek S. Structural assessment of a solid propellant rocket motor: effects of aging and damage[J].AerospaceScienceandTechnology, 2011, 15(8): 635-641.

[19] 李恩奇, 雷勇军, 袁端才, 等. 某固体火箭发动机药柱的动力学分析[J]. 固体火箭技术, 2007, 30(6): 486-489.

LI En-Qi, LEI Yong-jun, YUAN Duan-cai, et al. Dynamic analysis on X-type solid rocket motor grain[J].JournalofSolidRocketTechnology, 2007, 30(6): 486-489.

[20] 曲凯, 邢耀国, 张旭东. 摇摆载荷作用下舰载固体火箭发动机药柱疲劳损伤[J]. 航空动力学报, 2011, 26(11): 2636-2640.

QU Kai, XING Yao-guo, ZHANG Xu-dong. Fatigue damage of shipborne solid rocket motor propellant under swing loading[J].JournalofAerospacePower, 2011, 26(11): 2636-2640.

[21] 曲凯, 张杰, 张旭东. 舰船运动对固体火箭发动机粘接界面疲劳损伤研究[J]. 兵工学报, 2012, 33(8): 986-990.

QU Kai, ZHANG Jie, ZHANG Xu-dong. Research on effects of ship motion on interface fatigue damage of solid rocket motor[J].ActaArmamentarii, 2012, 33(8): 986-990.

[22] 李记威, 房雷, 周建军, 等. 某空空导弹发动机装药挂飞振动疲劳寿命分析[J]. 弹箭与制导学报, 2016, 36(1): 89-92.

LI Ji-wei, FANG Lei, ZHOU Jian-jun, et al. Fatigue life analysis for a solid rocket motor of air-to-air missile under hanging flight vibration[J].JournalofProjectilesRocketsMissilesandGuidance, 2016, 36(1): 89-92.

[23] ZHANG Wei-yao, GAO Jing-bo, WANG Cong. Rigid-flexible coupling dynamic analysis of sub-Launched vehicle during the vertical tube-exit stage[J].JournalofHarbinInstituteofTechnology(NewSeries), 2015, 22(2): 26-33.