全国名校导数综合测试题

全国名校导数综合测试题

■河南省许昌高级中学 胡银伟

一、选择题(本大题共1 2小题,每小题5分,共6 0分。)

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

3.设f(x)=xl nx,若f'(x0)=2,则x0=( )。

A.e2B.e CD.l n2

4.若函数f(x)=x3-2c x2+x有极值点,则实数c的取值范围为( )。

5.若曲线y=x2+al nx(a＞0)上任意一点处的切线斜率为k,若k的最小值为4,则此时该切点的坐标为( )。

A.(1,1) B.(2,3)

C.(3,1) D.(1,4)

A.[-5,0) B.(-5,0)

C.[-3,0) D.(-3,0)

7.若函数f(x)=2x2-l nx在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )。

8.当a＞0时,函数f(x)=(x2-2a x)ex的图像大致是( )。

A. B. C. D.

9.已知函数f(x)=x(l nx-a x)有两个极值点,则实数a的取值范围是( )。

C.(0,1) D.(0,+∞)

(-2,0)时,f(x)的最小值为1,则a的值等于( )。

1 1.若定义在R上的函数f(x)满足f(x)+ f'(x)＞1,f(0)=4,则不等式(e为自然对数的底数)的解集为( )。

A.(0,+∞)

B.(-∞,0)∪(3,+∞)

C.(-∞,0)∪(0,+∞)

D.(3,+∞)

1 2.已知函数g(x)=a-x2为自然对数的底数)与h(x)= 2 l nx的图像上存在关于x轴对称的点,则实数a的取值范围是( )。

二、填空题(本大题共4小题,每小题5分,共2 0分。) 1

1 5.已知函数f(x)(x∈R)满足f(1)= 1,且f(x)的导数f'(x)＜1,则不等式2的解集为。

三、解答题(本大题共6小题,共7 0分。)

(1)若f(x)与g(x)在x=1处相切,求g(x)的表达式;

1 8.(本小题满分1 2分)已知函数f(x) =2 l nx-x2+a x(a∈R)。

(1)当a=2时,求f(x)的图像在x=1处的切线方程;

1 9.(本小题满分1 2分)某分公司经销某种品牌产品,每件产品的成本为3 0元,并且每件产品需向总公司缴纳a元(a为常数,2≤a≤5)的管理费,根据多年的统计经验,预计当每件产品的售价为x元时,产品一年的销售量为(e为自然对数的底数)万件,已知每件产品的售价为4 0元时,该产品一年的销售量为5 0 0万件。经物价部门核定每件产品的售价x最低不低于3 5元,最高不超过4 1元。

(1)求分公司经营该产品一年的利润L(x)万元与每件产品的售价x元的函数关系式。

(2)当每件产品的售价为多少元时,该产品一年的利润L(x)最大?并求出L(x)的最大值。

2 0.(本小题满分1 2分)已知a为实数,函数f(x)=al nx+x2-4x。

(1)是否存在实数a,使得f(x)在x=1处取得极值?证明你的结论;

(2)设g(x)=(a-2)x,若∃x0∈。

(1)求f(x)的单调区间;

(2)设g(x)=x2-2x,若对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)＜g(x2),求a的取值范围。

2 2.(本小题满分1 2分)已知函数f(x) =(a x2+x-1)ex,其中e是自然对数的底数,a∈R。

(1)若a=1,求曲线f(x)在点(1,f(1))处的切线方程;

(2)若a＜0,求f(x)的单调区间;

参考答案

3.B 提示：因为f'(x)=l nx+1,所以f'(x0)=l nx0+1=2,l nx0=1,x0=e。

4.D 提示：若函数f(x)=x3-2c x2+ x有极值点,则f'(x)=3x2-4c x+1=0有两个不等实根,故Δ=(-4c)2-1 2＞0。从而故实数c的取值范围为

5.A 提示：y=x2+al nx的定义域为(0,+∞),由导数的几何意义知y'=2x+a

6.C

8.B 提示：f'(x)=(x2-2a x)ex+(2x -2a)ex=ex[x2+(2-2a)x-2a]。令,故函数图像应该先增后减再增,排除A,D。当x＜0时,因为a＞0,所以f(x)=(x2-2a x)ex＞0。

9.B 提示：因为f(x)=x(l nx-a x),所以f'(x)=l nx-2a x+1。故f'(x)在(0,+∞)上有两个不同的零点,可令f'(x)则上单调递增,在(1,+∞)上单调递减。又因为当x→0时,g(x)→-∞,当x→+∞时,g(x)→0,而g(x)max=g(1)=1,所以只需0＜2a＜1⇒0

1 0.D 提示：因为f(x)是奇函数,所以f(x)在(0,2)上的最大值为-1。当x∈(0,

1 2.B 提示：由已知得到方程a-x2= -2 l nx,即-a=2 l nx-x2在[1 e,e]上有解。设f(x)=2 l nx-x2,求导得f'(x)=所以f'(x)=0在x=1有唯一的极值点。因为,故方程上有解等价于2-e2≤-a≤-1,所以实数a的取值范围是[1,e2-2]。

①若a≥0,当0＜x＜1时,f'(x)＞0, f(x)单调递增;当x＞1时,f'(x)＜0,f(x)单调递减;所以x=1是f(x)的极大值点。

综合①②得a的取值范围是(-1, +∞)。

故x2-(2m-2)x+1≥0在[1,+∞)上恒成立,则

1 8.(1)当a=2时,f(x)=2 l nx-x2+,切点坐标为(1,1),切线的斜率k=f'(1)=2,则切线方程为y-1=2(x-1),即y=2x-1。

当1＜x＜e时,g'(x)＜0。

故g(x)在x=1处取得极大值,g(1)= m-1。

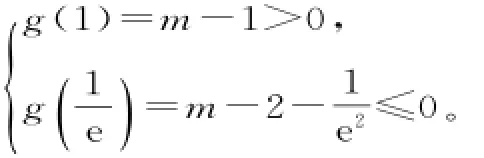
将x=4 0,y=5 0 0代入,得k=5 0 0 e40。

故该产品一年的销售量y(万件)关于x(元)的函数关系式为y=5 0 0 e40-x。

所以L(x)=(x-3 0-a)y=5 0 0(x-3 0-a)e40-x(3 5≤x≤4 1)。

(2)由(1)得,L'(x)=5 0 0[e40-x-(x-3 0-a)e40-x]=5 0 0 e40-x(3 1+a-x)。

①当2≤a≤4时,L'(x)≤5 0 0 e40-x(3 1+ 4-3 5)=0,当且仅当a=4,x=3 5时取等号。

所以L(x)在[3 5,4 1]上单调递减。

因此,L(x)max=L(3 5)=5 0 0(5-a)e5。

②当4＜a≤5时,L'(x)＞0⇔3 5≤x＜3 1+a,L'(x)＜0⇔3 1+a＜x≤4 1。

所以L(x)在[3 5,3 1+a)上单调递增,在[3 1+a,4 1]上单调递减。

因此,L(x)max=L(3 1+a)=5 0 0 e9-a。

综上所述当2≤a≤4时,每件产品的售价为3 5元,该产品一年的利润L(x)最大,最大利润为5 0 0(5-a)e5万元;

当4＜a≤5时,每件产品的售价为(3 1+ a)元时,该产品一年的利润L(x)最大,最大利润为5 0 0 e9-a万元。

假设存在实数a,使f(x)在x=1处取极值,则f'(1)=0,a=2。

故不存在实数a,使得f(x)在x=1处取得极值。

(2)由f(x0)≤g(x0),得：

(x0-l nx0)a≥x20-2x0。

当0＜x＜1时,F'(x)＜0,单调递减;

当x＞1时,F'(x)＞0,单调递增。

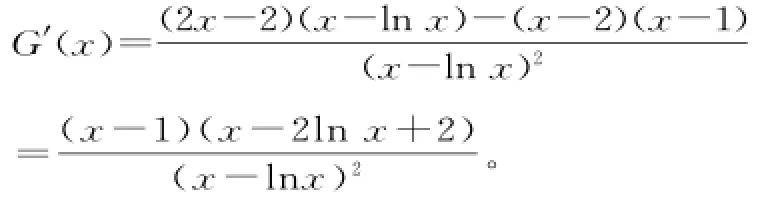
因为G'(x)＜0,G(x)单调递减;当x∈(1,e)时, G'(x)＞0,G(x)单调递增,G(x)min=G(1) =-1,a≥G(x)min=-1。

因此,实数a的取值范围为[-1,+∞)。

①当a≤0时,x＞0,a x-1＜0,在区间(0,2)上,f'(x)＞0,在区间(2,+∞)上f'(x)＜0,故f(x)的单调递增区间是(0, 2),单调递减区间是(2,+∞)。

f(x)的单调递增区间是(0,+∞)。

(2)由已知,在(0,2]上有f(x)max＜g(x)max。

由已知,g(x)max=0,由(1)可知,

所以,-2a-2+2 l n2＜0,a＞l n2-1。

综上,a的取值范围为(l n2-1,+∞)。

2 2.(1)a=1时,f(x)=(x2+x-1)ex,所以f'(x)=(2x+1)ex+(x2+x-1)ex= (x2+3x)ex。

曲线f(x)在点(1,f(1))处的切线斜率为k=f'(1)=4 e。

又因为f(1)=e,所以所求切线方程为y-e=4 e(x-1),即4 ex-y-3 e=0。

(2)f'(x)=(2a x+1)ex+(a x2+x-1)· ex=[a x2+(2a+1)x]ex。

(3)当a=-1时,f(x)=(-x2+x-1)· ex,由(2)知,f(x)=(-x2+x-1)ex在(-∞,-1]上单调递减,在[-1,0]上单调递增,在[0,+∞)上单调递减。

所以g(x)在(-∞,-1]上单调递增,在[-1,0]上单调递减,在[0,+∞)上单调递增。故g(x)在x=-1处取得极大值g(-1),在x=0处取得极小值g(0)=m。因为函数f(x)与函数g(x)的图像有3个不同的交点,所以

所以

(责任编辑 徐利杰)