一种识别声源噪声辐射区域的方法
2017-05-04苏俊博朱海潮苏常伟
苏俊博,朱海潮,苏常伟
(海军工程大学 船舶振动噪声重点实验室,武汉 430033)
一种识别声源噪声辐射区域的方法
苏俊博,朱海潮,苏常伟
(海军工程大学 船舶振动噪声重点实验室,武汉 430033)
针对大型结构体的声辐射问题,提出了一种利用声辐射模态识别声源表面的噪声辐射区域的方法。分析了各阶声辐射模态对声源的辐射声功率的贡献量,找出了对远场辐射声功率贡献最大的几个主要的声辐射模态,然后利用这几个主要的声辐射模态重建声源表面法向振速,通过声源表面法向振速的重建结果实现了声源表面噪声辐射区域的识别。通过对平板声源在几种不同频率下的噪声辐射区域的仿真分析验证了文中方法的正确性。该文方法对于确定特定频率下声源表面的噪声辐射区域,从而进一步进行辐射噪声控制具有积极的意义。
噪声辐射区域;声辐射模态;辐射声功率;声场重建;减振降噪
0 引 言
为降低飞机、船舶等大型结构体的噪声,准确识别结构体表面的噪声辐射区域具有很重要的意义。近年来近场声全息技术在噪声源的识别与定位方面取得了很大的成功[1-2],然而降低结构体的辐射噪声与减小噪声源的振动之间并没有必然的直接联系,减振而不降噪的情况经常出现。这是因为声源表面振动在波数域中可分为超声速波数成分和亚声速波数成分[2],而仅有部分的波数成分能够对远场的辐射噪声产生影响,以无限大平板为例,对远场辐射有贡献的仅为波数域中的超声速波数成分。因此声源表面振动最大的区域的噪声辐射能力并不一定最强。对于降低远场辐射噪声而言,准确识别声源结构表面的噪声辐射区域比噪声源的识别与定位更有意义。Williams[3-4]利用超声速声强来识别声源结构表面的噪声辐射区域,Magelhaes和Tenenbaum[5]将超声速声强技术扩展到任意结构的声源。由于超声速声强技术是基于辐射圆内部的波数成分积分得到,而对有限体积的结构,辐射圆外部的一些波数成分仍然能够向远场辐射噪声,因此超声强技术的计算结果并不是足够准确。声辐射模态理论[6-7]的提出为解决这一问题提供了新的途径。Marburg[8]利用声辐射模态理论构造了一个声源表面辐射声功率贡献因子,用来评价声源结构表面各部分对远场辐射噪声的贡献。本文基于声辐射模态理论,提出了一种不同于Marburg计算表面声功率辐射贡献因子的方法,首先找出了对远场辐射声功率贡献最大的几个主要的声辐射模态,然后利用这几个主要的声辐射模态重建声源表面法向振速,通过声源表面法向振速的重建结果即可实现声源表面噪声辐射区域的识别。该方法相对于Marburg方法的优点在于实现噪声辐射区域识别的同时,找出了对远场辐射声功率贡献最大的几个主要的声辐射模态,有利于进一步利用声辐射模态理论对声源的辐射噪声进行控制。
1 声源噪声辐射区域的识别
将声源表面离散成一系列等面积的辐射单元,其辐射声功率可表示为[9]

其中:R=(s/ 2) Re[Z],Z为辐射声阻抗,s为辐射单元面积,v为声源表面速度向量。将R进行特征值分解:

其中:Φ为N×N维矩阵,Φ的列向量φi( i=1,2,…N )即为声辐射模态向量。Λ=diag[λ1,λ2,…,λi,…]是以特征值为对角线元素的对角矩阵,特征值在对角线上按由大到小的顺序依次排列。由于特征值与对应的声辐射模态的辐射效率成正比,因此声辐射模态向量在声辐射模态矩阵Φ中按照辐射效率的大小由低到高依次排列。为了更好地说明声辐射模态的这个性质,选择一正方形简支钢板,对其声辐射模态在波数域的波数谱进行分析。假设正方形钢板边长为0.5m,分析频率为380 Hz,则平板前十阶声辐射模态对应的波数谱如图1所示。
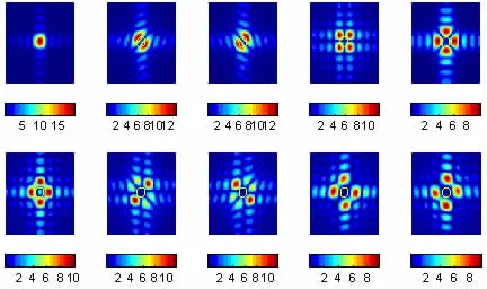
图1 平板前十阶声辐射模态的波数谱Fig.1 The wave number spectrum of the front ten acoustic radiationmodes
图1中声辐射模态波数谱图中的圆圈代表辐射圆,从图中可以看出,在此分析频率下,辐射圆内部包含主要波数成分的声辐射模态主要是前六阶,并且辐射圆内包含的主要波数成分随着阶数的增大逐渐减少。这解释了声辐射模态随着阶数的增大辐射效率逐渐降低的原因。但是仅以辐射圆内部是否包含主要波数成分来判断该阶声辐射模态是否对远场辐射有影响不够准确,因为根据边角模态辐射理论,对于有限体积的声源,辐射圆外部的少数波数成分仍然能向远场辐射能量。本文中以辐射声功率来确定向远场辐射噪声的主要声辐射模态,具体方法将在下节论述。假定向远场辐射噪声的主要的声辐射模态有M阶,利用这M阶声辐射模态重建声源表面的法向振速分布,则重建的法向振速分布就是向远场辐射噪声的振动形式,声源表面重建法向振速幅值较大的区域代表了向远场辐射噪声的区域。具体重建过程如下。
声源结构表面的法向速度向量可用声辐射模态表示成如下形式

其中:c为辐射模态展开系数。假设将辐射体表面离散成N个辐射单元,并计算得到了N阶声辐射模态。由于(3)式具有良好的收敛性[10],用少量的声辐射模态就可近似地表示出振速向量,因此表面速度可用截断的声辐射模态表示为

其中:矩阵Φ(N×N1)表示只取了前N1阶声辐射模态。当辐射体表面速度向量中有N2个元素是已知的,可以得到由这N2个元素组成的方程组

为保证(5)式的适定性,辐射体表面速度向量中已知元素的数量大于声辐射模态的数量即可,而不要求知道辐射体表面全部的法向速度。由(5)式可以求得声辐射模态系数

其中:(Φ′)+(N1×N2)是Φ′(N2×N1)的伪逆。
利用M阶主要的声辐射模态可由(7)式对声源表面法向振速中向远场辐射噪声的部分
其中:Φ0为由M阶主要的声辐射模态组成的矩阵,c0为这M阶声辐射模态对应的声辐射模态展开系数。
2 仿真验证
本节通过对一带有无限大障板的平板的数值仿真验证本文方法的有效性,并在本节中提出了寻找对远场辐射噪声有贡献的声辐射模态的方法。本节中选取一个受单点简谐激励的四周为无限大障板的简支钢质平板为研究对象。平板的长度、宽度和厚度为Lx×Ly×h=0.5m×0.5m× 0.008 m,杨氏模量E取2×1011Pa,υ为泊松比取0.28,材料密度ρ0=7 800 kg/m3,空气中声速c0=343 m/s。用公式(8)计算该简支板的模态频率,可知该简支板的(1,1)、(2,2)、(3,3)阶模态频率分别为153 Hz,612 Hz,1 378 Hz。

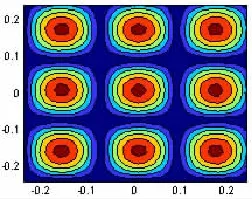
图2 1 378 Hz激励下平板表面法向振速幅值Fig.2 The amplitude of velocity of the plate at the exciting frequency of 1 378 Hz
当以频率为1 378 Hz、幅值为10 N的简谐力激励平板,平板将以(3,3)阶模态振动。将平板表面均匀分为32×32个面积单元,其表面法向振速幅值如图2所示。本节将对以(3,3)阶模态振动的该简支平板在不同分析频率下的噪声辐射区域进行分析。
2.1 确定辐射声功率的主要声辐射模态
能否找出对远场辐射噪声有主要贡献的声辐射模态,对声源表面的噪声辐射区域的识别结果的准确与否有着至关重要的影响。声辐射模态对远场辐射噪声的贡献可以用该阶声辐射模态的辐射声功率表示,而声源的辐射声功率可以表示成如下的形式[7]

其中:λi为第i阶声辐射模态对应的特征值,ci为声辐射模态展开系数。用前M阶声辐射模态的辐射声功率来估计声源的辐射声功率,则声源的辐射声功率的估计误差可由下式表示:

对于上述由简谐力激励的简支平板而言,分析频率为300 Hz时,该简支平板的辐射声功率的估计误差与声辐射模态的截止阶数之间的关系如图3所示。从图3中辐射声功率的估计误差与声辐射模态的截止阶数之间的关系曲线中可以看出,辐射声功率的估计误差随声辐射模态截止阶数的增大迅速减小,因此只有前面少量的声辐射模态对远场的辐射噪声产生影响。更需要引起重视的是,在图3中的局部放大图中可以看到在2-5阶,6-10阶,辐射声功率的估计误差并没有随着截止阶数的增大而降低,这说明在平板此种振动形式下3-5阶、7-10阶声辐射模态对辐射声功率基本没有贡献,不是辐射声功率的主要声辐射模态,这些模态的存在对声源表面噪声辐射区域的识别造成干扰,所以在重建声源表面的法向振速时要将这些非主要声辐射模态去除。第i阶声辐射模态的辐射声功率可由下式计算得到:


图3 辐射声功率估计误差Fig.3 The estimation error of radiated sound power

图4 辐射声功率估计误差(重新排序)Fig.4 The estimation error of radiated sound power (rearranged acoustic radiationmodes)
将声辐射模态按辐射声功率由大到小重新进行排序,并再次计算辐射声功率的估计误差,得到图4。从图4中可以看出,经过重新排序后,辐射声功率估计误差在声辐射模态截止阶数为2时就下降到了1.5‰,因此辐射声功率的主要模态为前两阶,此时的前两阶声辐射模态即为未重新排序以前的第一阶和第六阶声辐射模态,利用此两阶声辐射模态重建平板表面法向振速,即可实现对平板表面噪声辐射区域的识别。
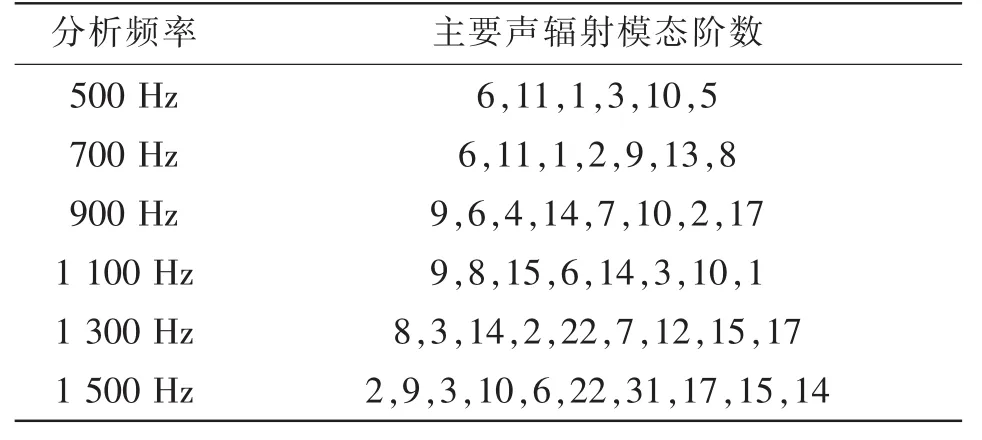
表1 各分析频率下平板的主要声辐射模态Tab.1 The dom inant acoustic radiation modes at the analyzing frequencies
当分析频率为500 Hz、700 Hz、900 Hz、1 100 Hz、1 300 Hz和1 500 Hz时,经分析得到的辐射声功率的主要声辐射模态如表1所示。
2.2 平板声源的噪声辐射区域分析
由2.1节得到的各分析频率下向远场辐射噪声的主要声辐射模态,利用(7)式可完成对平板表面法向振速的重建,从而利用此重建结果可实现各分析频率下平板表面噪声辐射区域的识别。为验证本文方法的准确性,利用Marburg的方法做了同样的分析,并将本文得到的结果与Marburg的方法得到的结果作比对,如图5、图6所示。图5、图6中第一列是平板表面法向振速幅值,第二列是Marburg的方法得到的平板表面各区域对辐射声功率的贡献因子,第三列是本文方法重建得到的法向振速的幅值,图5中由上到下每一行分别是分析频率为300 Hz、500 Hz、700 Hz和900 Hz时的仿真结果,图6中由上到下每一行分别是分析频率为1 100 Hz、1 300 Hz和1 500 Hz时的仿真结果。
从图5、图6中可以观察到当分析频率在300-900 Hz时,平板表面的噪声辐射区域集中在四个角上,随着分析频率的继续增大,平板表面噪声辐射区域也越来越大,这样的分析结果与边角辐射模态理论一致。此外,通过对本文提出的方法得到的识别结果与Marburg的方法得到的结果进行比较可知二者基本一致,验证了本文方法对噪声辐射区域识别结果的准确性。由于本文中的方法在识别噪声辐射区域的过程中,首先找出了向远场辐射声功率的主要声辐射模态,这一结果不仅有利于声源表面噪声辐射区域的识别,而且对利用声辐射模态进行声辐射主动控制具有很重要的意义,可有效减少控制的通道数。
3 结 论
本文提出了一种识别声源表面噪声辐射区域的方法,该方法利用对远场辐射声功率有贡献的声辐射模态重建声源表面振动,识别出了声源结构表面向远场辐射噪声的区域。前面的研究表明:(1)各阶声辐射模态之间能够实现辐射声功率解耦,声源的辐射声功率能够用各阶声辐射模态的辐射声功率的线性叠加表示,并且存在对远场辐射声功率贡献较大的几个主要的声辐射模态,利用这几个主要的声辐射模态重建声源表面法向振速即可实现对声源噪声辐射区域的识别;(2)声源结构表面振动最大的区域并不一定是对远场辐射声功率贡献最大的区域,当选定的分析频率远小于结构声源的激励频率时,声源表面的边角部分对辐射声功率贡献最大。本文中是以平板声源为研究对象,但本文的研究方法和结论同样适用于具有其他几何外形的声源。
[1]Maynard JD,Williams E G,Lee Y.Near field acoustic holography I.Theory of generalized holography and the developmentof NAH[J].JAcoust.Soc.Am.,1985,78(4):1395-1413.
[2]Williams Earl G.Fourier acoustics:Sound radiation and nearfield acoustical holography[M].London:Academic Press, 1999:28-35.
[3]Williams E.Supersonic acoustic intensity[J].JAcoust.Soc.Am.,1995,97(1):121-127.
[4]Williams E.Supersonic acoustic intensity on planar sources[J].JAcoust.Soc.Am.,1998,104(5):2845-2850.
[5]Magelhaes M B S,Tenenbaum R B.Supersonic acoustic intensityfor arbitrarily shaped sources[J].Acta Acust.Acust., 2006,92:189-201.
[6]Borgiotti G V.The power radiated by a vibrating body in an acoustic fluid and its determination from boundary measurements[J].JAcoust.Soc.Am.,1990,88(4):1884-1893.
[7]Cunefare K A.The design sensitivity and control of acoustic power radiated by three-dimensional structures[D].Ph.D.thesis,The Pennsylvania State University,1990.
[8]Steffen Marburg.Surface contributions to radiated sound power[J].JAcoust.Soc.Am.,2013,133(6):3700-3705.
[9]Elliott S J,Johnson M E.Radiation modes and the active control of sound power[J].JAcoust.Soc.Am.,1993,94(4): 2194-2204.
[10]聂永发,朱海潮.利用源强密度声辐射模态重建声场[J].物理学报,2014,63(10):104303. Nie YongFa,Zhu Haichao.Acoustic field reconstruction using source strength density acoustic radiation modes[J].Acta Phys.Sin.,2014,63(10):104303.
A method to identify the noise radiation regions on the surface of acoustic source
SU Jun-bo,ZHU Hai-chao,SU Chang-wei
(National Key Laboratory on Ship Vibration&Noise,Naval University of Engineering,Wuhan 430033,China)
For the acoustic radiation problems of large scale vibrating structure,amethod based on acoustic radiationmodes is proposed to identify the noise radiation regions on the structure.To identify the noise radiation regions on the surface of acoustic source,the contributions of acoustic radiationmodes to radiated sound power are analyzed,and themain acoustic radiationmodes,which have themost contribution to the radiated sound power,are selected.By the selected acoustic radiationmodes,the velocities on the surface are reconstructed.The identification of noise radiation regions is realized by the reconstructed resultof the velocities.The validity of the proposedmethod is validated by numerical simulating for the noise radiation regions of a rectangular plate at several frequencies.The proposed method has a positive significance for identifying the noise radiation regions of acoustic source and further reducing the radiation noise in the farfield.
noise radiation regions;acoustic radiationmodes;radiated sound power; acoustic field reconstruction;vibration and noise reduction
TB532 TB533
:Adoi:10.3969/j.issn.1007-7294.2017.02.014
2016-06-14
国家自然科学基金项目(51305452)
苏俊博(1985-),男,博士研究生,E-mail:sujunbo0618@163.com;
朱海潮(1963-),男,教授,博士生导师。
1007-7294(2017)02-0237-07
