基于ALE算法的无转角和有转角铝制加筋板楔形体水弹性砰击的数值模拟研究

骆寒冰，董德龙，季红叶，赵中榜，高 原

（天津大学 a.水利工程仿真与安全国家重点实验室；b.船舶与海洋工程系，天津 300072）

基于ALE算法的无转角和有转角铝制加筋板楔形体水弹性砰击的数值模拟研究

骆寒冰a，b，董德龙b，季红叶b，赵中榜b，高 原b

（天津大学 a.水利工程仿真与安全国家重点实验室；b.船舶与海洋工程系，天津 300072）

文章采用基于任意拉格朗日—欧拉（ALE）算法的显式有限元技术研究水弹性砰击现象，针对已开展的铝制加筋板楔形体结构入水砰击模型实验，开展了数值模拟比较工作。该楔形体底部斜升角为20度，底部两侧是包含三根纵骨和两根横梁的加筋板结构，两侧结构刚度不同。预报了模型无转角和有转角典型工况的砰击入水过程，得到的入水加速度、底部加筋板结构纵骨应力和横梁响应与模型实验结果吻合较好。研究表明该ALE算法具备模拟船舶局部结构的水弹性砰击流固耦合问题的能力。

ALE算法；铝制加筋板结构；水弹性砰击；转角；数值计算

0 引 言

在波浪中高速航行船舶的首部容易遭受严重的水动力砰击作用[1]。准确预报砰击载荷并合理确定其设计载荷是艏部结构设计的一个难题。砰击载荷在复杂船首外表面的时间和空间分布很复杂。船首局部加筋板结构设计时候，通常把这复杂的水动力载荷简化为准静态的、均匀分布的载荷处理，这与实际的时空分布相比差异很大。而且，当局部结构的斜升角较小时，或者砰击载荷的持续时间和局部结构的固有周期接近时，Faltinsen[2]指出，需要考虑局部结构的水弹性效应，砰击问题应当作水动力学和结构力学的联合体来研究，即需要同时分析砰击载荷和结构动响应的时间和空间分布特性。

由于砰击问题的复杂性，采用解析或半解析方法研究水弹性砰击机理时候，通常把复杂结构简化成二维的楔形体、圆柱体等，分析结构落体到平静水面的典型入水问题。通常流体域采用势流理论，结构域采用有限元（FEM）方法，来考虑结构和流体两者之间耦合作用。如卢炽华等[3]结合边界元方法（BEM）和FEM法，分析二维弹性楔形体砰击，Sun和Faltinsen[4]结合BEM和结构解析方法，研究圆柱壳体水弹性砰击。Korobkin等[5]采用Wagner[6]理论和梁有限元方法，分析二维弹性楔形体的水弹性效应。除了典型的回转体这类简单结构之外，目前对三维水弹性砰击研究尚不多见。如Peseux等[7]采用三维Wagner理论和FEM法，分析了圆锥体砰击问题。

近年来，基于显式有限元技术的数值方法开始应用于砰击问题。Stenius等[8]应用显式有限元LSDYNA软件的ALE算法研究二维楔形体刚体入水砰击问题，Stenius等[9]还探讨了二维弹性体的水弹性效应。Aquelet等[10]讨论了LS-DYNA软件预报砰击时罚函数耦合算法对计算结果的影响。Luo等[11]针对二维刚体砰击讨论了网格大小对数值模拟结果精度的影响。Luo等[12]选取船舶最基本的结构—加筋板结构，应用ALE方法数值分析了某加筋板楔形体入水砰击问题，预报的加速度和结构应力响应与实验吻合较好。由于需要描述局部流体砰击射流，LS-DYNA数值模拟时候要求流体的网格很小，网格才不会畸变，导致时间步长变得很小，模型的网格数量大，在微机上计算时间很长，骆寒冰等[13]研究了并行计算技术来提高计算效率。上述研究表明，基于ALE算法的显式有限元技术在砰击预报上有很好的应用前景，具备预报结构水弹性砰击的潜力，但是，如果要推广应用到船舶上，还需要继续做数值验证工作。

目前，针对有转角结构水弹性砰击的研究还较少见，而船舶在首斜浪航行时候，会有明显的横摇运动，此时船首入水砰击的斜升角会比顶浪时候的要小，角度小时候水弹性效应可能更明显，因此，研究有转角工况具有重要的工程应用价值。本文根据最近在天津大学进行的铝制加筋板楔形体入水模型实验[14]，应用基于ALE算法的显式有限元技术，开展数值预报工作，分析在无转角和有转角情况下模型结构的入水砰击过程，预报砰击加速度和结构应力响应，与模型实验结果进行对比分析。通过本文的研究，验证算法在上述问题上的适用性，为今后应用本方法预报实际船舶结构水弹性砰击做技术储备。

1 基于ALE算法的显式有限元技术

ALE算法最早出现于数值模拟流体动力学问题的有限差分方法中。该算法同时具备Lagrange方法和 Euler方法两者的特长[15-16]。引进了Lagrange方法的特点来处理结构边界运动，能够有效地跟踪物质结构边界的运动；吸收了Euler方法的长处来划分内部网格，使内部网格单元独立于物质实体而存在，不同于Euler方法的是，ALE方法网格可以根据定义的参数在求解过程中适当地调整位置，使得网格不致出现严重的畸变。这种方法在处理整个物体有空间的大位移并且本身有大变形的问题时非常有优势，可以克服单元严重畸变引起的数值计算困难，并可以实现流体—固体耦合的动态分析。

在软件LS-DYNA[17]中水和空气采用空白材料模型与状态方程联用表示，多物质欧拉网格，自由表面的生成利用VOF方法，结构采用弹性材料模型，拉格朗日网格。在欧拉流体和拉格朗日固体接触面，采用罚函数耦合算法，可以模拟流体与固体之间的耦合效应。罚函数偶合系数追踪拉格朗日节点（结构，从物质）和欧拉流体（主物质）物质位置间的相对位移d，检查每一个主从节点对主物质表面的贯穿，如果从节点不出现贯穿，就不进行任何操作；如果发生从节点对主物质表面的贯穿，界面力F就会分布到欧拉流体的节点上。界面力的大小与发生的贯穿数量成正比：

式中：ki表示基于主从节点质量模型特性的刚度系数。

由于采用了上述任意的拉格朗日—欧拉（ALE）算法和罚函数耦合算法，LS-DYNA具备模拟水弹性砰击流固耦合问题的能力。

2 铝制加筋板楔形体入水砰击实验介绍

设计了一个铝制三维加筋板楔形体模型，其主尺度长×宽×高为：1.440m×1.354m×0.746m。图1是模型典型剖面结构示意图。模型底部斜升角为20°，模型结构质量180 kg。底部两侧是包含三根‘1’字形纵骨和两根‘T’字形横梁的加筋板结构，是实验测试区域。底部左右两侧的外板厚度分别为4 mm、3mm，两侧的纵骨和横梁的尺寸及厚度不同，通过这样的设计，在一次落体砰击实验中可以测试得到两组不同刚度结构的应变响应结果。模型上部结构刚度设计得比较大，采用的铝板厚度为8mm，目的是给底部加筋板结构提供一个刚性的四周边界条件。模型前后端的挡板向楔形体下方做了适当延伸，目的是减少落体模型入水砰击的三维效应。

图1 模型典型横剖面结构示意图Fig.1 Mid-section structure of themodel

图2 实验模型测点布置示意图Fig.2 Distribution ofmeasuring points on themodel

图3 无转角入水砰击过程典型照片（高度1.20m）Fig.3 Photos forwater entry without roll angle(height1.20m)

模型实验主要测量入水砰击过程的落体加速度、底部外板的砰击压力，底部加筋板结构的应变动响应等参数。测点布置见图2。模型纵桁前后布置2个加速度测点（以A为首字母），测量垂向入水加速度；底部外板板格的中心位置共布置了8个砰击压力测点（以P为首字母），测量垂直于外板的砰击压力；在纵骨上表面、纵向中间的位置粘贴18个应变片，在横梁面板上表面、横向粘贴8个应变片，合计26个应变测点（以S为首字母）。实验总共36个测点。

在天津大学建造了一个实验水池，其主尺度长×宽×高为：5.00m×4.40m×1.30m。实验时候水池水深为1.20m。在实验水池上方设计安装了一个门字架，在门字架内侧垂直安装了两个不锈钢圆柱导轨。模型的前后档板上部分别固定两个滑动轴承，滑动轴承套在圆柱导轨上，滑动轴承的摩擦阻力可以忽略不计，于是利用该导轨可以确保模型是垂直入水的。在门字架一侧安装了一套手动葫芦和滑轮组，用于人工升降模型。设计了一套释放/抱紧装置，一端与模型连接，另一端与钢丝绳连接。通过人工启动释放/抱紧装置的释放开关，可以实现瞬间模型自由下落入水砰击。通过调整安装在模型前后档板上滑动轴承的位置，模型还可以旋转一定的角度，进行不同角度的入水砰击实验。

对于无转角砰击实验工况，落体高度分别为0.30 m、0.50 m、0.75 m、1.00 m、1.20 m和 1.40 m。有转角实验工况包括左转5°和右转5°两大类，落体高度分别为0.30 m、0.50 m和0.75 m。每组工况进行不少于3次的重复实验。实验数据采样频率10 kHz。图3显示了1.20m高度时候无转角入水砰击实验的典型照片，观测到了明显的射流。图4显示了0.50m高度、右转动5°时候模型实验照片。

图4 模型右转5°时落体实验照片（高度0.50m）Fig.4 Photos forwater entrymodelswith roll angle 5 degrees starboard side(height0.50m)

3 无转角入水砰击结果比较

对于上述铝制三维加筋板楔形体的入水实验，建立计算模型，采用LS-DYNA软件中的ALE算法和罚函数耦合算法，数值模拟水弹性砰击过程。由于模型四周和上部结构的板比底部板厚，为提高流固耦合计算效率，只考虑加筋板结构为弹性，分析其与流体的耦合问题，模型四周和上部结构简化处理为刚体。为了减少计算时间，初始入水高度设为0.055m，可以充分减少计算时间，根据公式 ，可以确定不同高度下落时对应的模型的初始速度。数值模拟实际实验的时间长度为0.15 s。

图5 无转角入水砰击LS-DYNA计算3D模型 Fig.5 3Dmodelwithout roll angle forwater entry in LS-DYNA

图6 无转角入水砰击流体域网格划分Fig.6 Meshes in air and water domain ofmodel without roll angle

为了提高计算精度，建立了左右两个模型，即根据对称面X=0，针对楔形体左、右侧底部加筋板结构，分别建立了一半模型。对称面采用了对称条件，无反射边界条件施加于除对称面以外的外部边界。整个落体模型质量为190 kg，包括结构质量180 kg，轴承和螺栓共6 kg，测量传感器及导线估算4 kg，那么一半模型的质量为95 kg。图5显示了无转角入水砰击的左侧的LS-DYNA计算模型。

流体区域采用非均匀网格。距离楔形体近的网格为均匀布置，其它区域，距离楔形体越远，网格尺寸越大。为能够合理反映结构应变响应，纵骨在垂向上划分了4个单元。水和空气的流体域单元数量总共489 280个，底部外板厚度为3 mm的右侧模型结构单元数量7 264个，底部外板厚度为4 mm的左侧模型结构单元数量8 120个。图6显示了左侧计算模型的流体域网格划分情况。

选取落体高度为1.20m典型工况，对数值计算和模型实验的入水加速度和结构动响应结果进行比较。图7显示了加速度时域曲线比较情况，其中，实验加速度开始突变时刻34.084 5 s，作为结构开始入水砰击的时间，“A1-Test”表示实验A1测点的结果，而“A-Num.”表示加速度数值模拟结果。图8显示了结构应力时域曲线比较情况。S13、S12和S11是左侧纵骨上纵向应力测点，分别对应右侧测点S14、S15和S16，S17和S18是左侧横梁面板上横向应力测点，对应右侧测点为S20、S19。图8中，“S13-Test”表示实验S13测点的结果，“S13-Num.”表示S13数值模拟结果，其它标注含义以此类推。从图7、8比较中可以看出：

图7 砰击加速度实验与数值计算比较（高度1.20m）Fig.7 Comparison of the impactacceleration(height1.20m)

（1）模型实验和数值模拟的加速度和和结构应力响应在时域上吻合很好，正确反映了整个入水过程，首先在时间34.084 5 s加速度突变，模型开始入水，接着应变测点信号从模型底部向上陆续出现响应；

（2）模型前后加速度测点A1、A2在变化趋势和极值响应上吻合好，峰值出现的时间分别是34.095 2s、34.095 4 s，大小分别是135.8 m/s2、129.4m/s2，可以推断出模型前后是同时入水的；数值预报的加速度峰值为139.3m/s2，略大于实验测试结果，出现的时间是34.094 2 s，略早于实验时间；

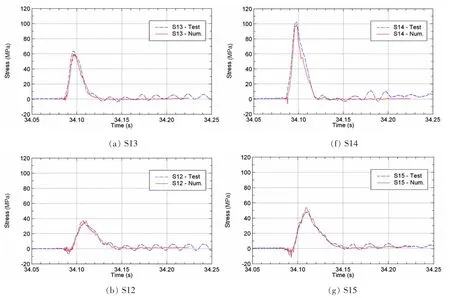
图8 砰击结构应力实验与数值计算比较（高度1.20m）Fig.8 Comparison of stress responses(height1.20m)

（3）左侧结构应力比右侧的要小，这是由于左侧底部加筋板结构的刚度比右侧的大，在受到相同的外界压力载荷情况下，左侧纵骨和横梁上的应力响应就小一些；纵骨应力是我们关注的重点，比横梁上应力要大；

（4）靠近模型底部的纵骨应力最大。对于左侧底部结构，纵骨测点S13应力响应峰值最大，实验和数值模拟分别为63.7 MPa、59.7 MPa，出现的时间分别为34.096 1 s、34.096 7 s；对于右侧底部结构，纵骨测点S14应力响应峰值最大，实验和数值模拟分别为102.3 MPa、98.8 MPa，出现的时间分别为34.097 2 s、34.097 7 s；

（5）左右两侧结构对应测点位置的应力响应出现峰值、增大和减少变化趋势相同，反映实验入水过程保持左右对称垂直入水，左右斜升角一样；

（6）实验纵骨测点的应力在峰值后观测到一定的高频振荡，这是水弹性砰击的表现之一，不过，数值预报的振荡不太明显，在后续的数值研究中将继续探讨该问题。

4 有转角入水砰击结果比较

对于有转角入水问题，选取了落体高度0.50m、右转5°工况开展比较分析。建立了整个落体结构的计算模型g，模型水和空气的流体域单元数量总共544 640个，模型结构单元数量16 931个。流体域单元总数与前面无转角模型的相当，由于无转角模型只取了一半的流体域，所以本部分的模型网格密度比前部分的略稀疏些。外部边界施加无反射边界条件。图9显示了该数值计算模型的典型横剖面。结构质量设为190 k。初始入水高度设为0.055 m，数值模拟实际实验的时间长度为0.15 s。

图10、11分别显示了加速度时域曲线、结构应力时域曲线比较情况。从前部分无转角入水砰击结构应力结果来看，横梁上面板应力较小，本部分就不讨论横梁的应力情况。通过比较可以看出：

（1）对有转角情况，实验和数值模拟的加速度和和结构应力响应在时域上吻合很好。

（2）模型前后加速度测点A1、A2峰值出现的时间分别是10.848 3 s、10.849 7 s，大小分别是53.5m/s2、56.8m/s2，表明实验模型前后是同时入水的；数值预报的加速度峰值为61.4m/s2，出现的时间是10.849 6 s；

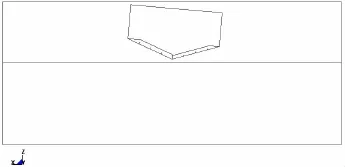
图9 右转5°入水砰击LS-DYNA计算模型Fig.9 Modelwith roll angle 5 degrees starboard for water entry in LS-DYNA

图10 砰击加速度实验与数值计算比较（高度0.50m，右转5°）Fig.10 Comparison of the impactacceleration(height 0.50m，roll angle 5 degrees starboard side)

（3）由于该模型右转5°，相当于左侧底部加筋板斜升角为25°，右侧的斜升角为15°，于是，入水过程中右侧的砰击压力大于左侧的，斜升角小一侧的湿长度相对大一些。对于左右对称的纵骨结构应力测点，右侧S14测点比左侧S13的先产生应力动响应，S14应力出现峰值的时间也比S13的早，同样适用于右侧S15与左侧S12、右侧S16与左侧S11之间的关系；

（4）对于左侧底部结构，纵骨测点S13应力响应峰值最大，实验和数值模拟分别为17.9MPa、18.7 MPa，出现的时间分别为10.855 4 s、10.855 0 s；对于右侧底部结构，纵骨测点S14应力响应峰值最大，实验和数值模拟分别为61.7 MPa、65.5MPa，出现的时间分别为10.850 0 s、10.849 3 s；

（5）图10数值模拟的加速度毛刺相对图7的多，入水砰击之前毛刺比较多，入水之后少一些，可能是加速度对模型流体单元网格密度要求高，而本部分模型的密度略小一些；相比较，无转角和有转角模型的结构应力预报的结果都很稳定。

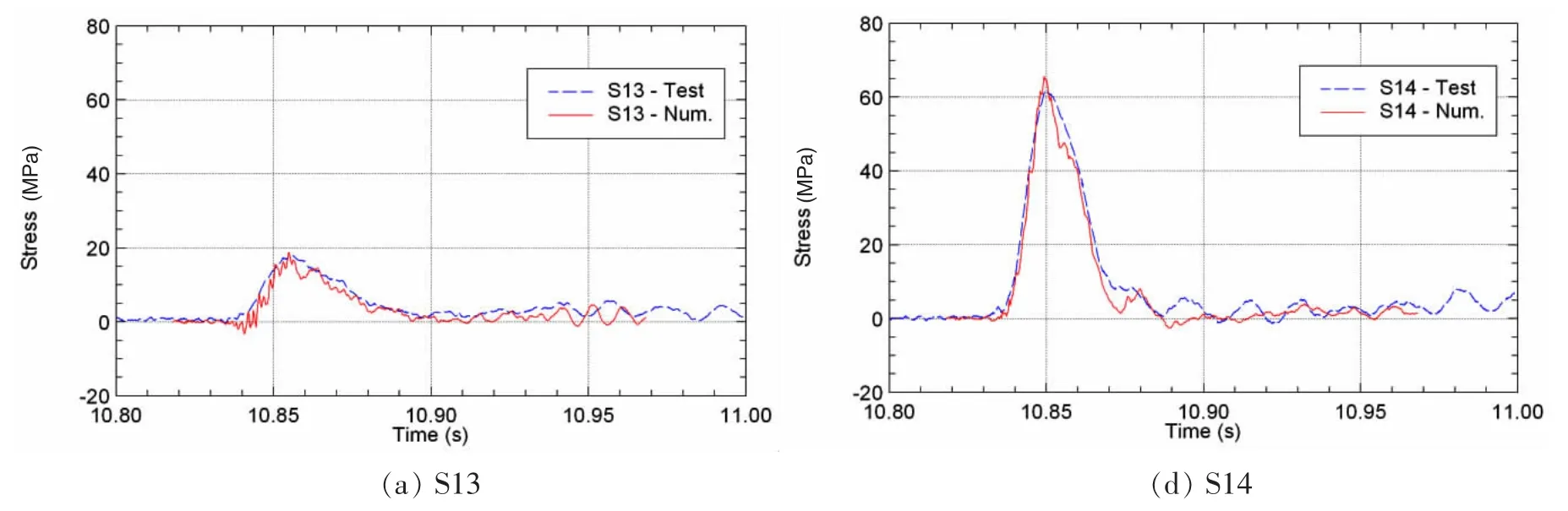
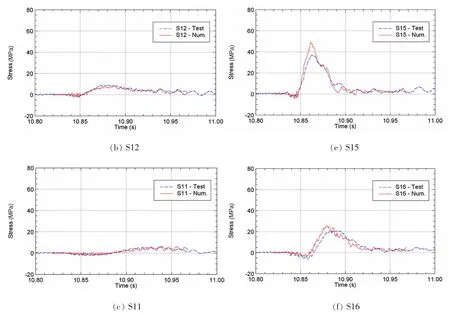
图11 砰击结构应力实验与数值计算比较（高度0.50m，右转5°）Fig.11 Comparison of stress responses(height 0.50m,roll angle 5 degrees starboard)

5 结 论

根据近期开展的铝制加筋板楔形体结构入水砰击模型实验的结果，本文开展了数值模拟比较工作。采用基于ALE算法和罚函数耦合算法的显式有限元技术，针对无转角和有转角入水砰击典型工况，数值模拟了入水过程中的加速度、纵骨上端纵向应力和横梁上面板横向应力响应，并与实验结果进行了比较，取得了以下结论：

（1）为了提高精度，减少计算时间，建立计算模型的时候，模型的底部加筋板结构采用了弹性材料，均匀网格，其它结构为刚性材料；流体区域采用了非均匀网格技术，距离楔形体底部近的，采用均匀布置，其它区域，距离越远，网格密度越小；

（2）对于无转角入水砰击工况，分别建立了左右两个模型进行分析。左右侧底部加筋板结构对称测点位置的应力响应在时间上的变化趋势相同，由于右侧的刚度比左侧的要小，因此右侧的应力大于左侧的；

（3）对于右转5°入水砰击工况，建立了一个整体模型进行分析。由于右侧底部斜升角小于左侧的，那么右侧结构对应纵骨测点应力响应峰值出现的时间早于左侧的。

（4）模型实验纵骨应力在峰值后观测到一定的高频振荡，而数值模拟的振荡现象不明显，今后需要继续深入研究该现象。

（5）数值模拟的加速度和应力响应与模型实验的结果在时域上吻合较好，这表明本文提出的水弹性砰击计算技术的合理性和可靠性，能够预报无转角和有转角入水砰击问题，具备推广到预报船首结构水弹性砰击的潜力。

参 考 文 献：

[1]骆寒冰,徐 慧,余建星,万正权.舰船砰击载荷及结构动响应研究综述[J].船舶力学,2010,14(4):439-450. Luo Hanbing,XüHui,YüJianxing,Wan Zhengquan.Review of the state of the art of dynamic responses induced by slamming loads on ship structures[J].Journal of Ship Mechanics,2010,14(4):439-450.(in Chinese)

[2]Faltinsen OM.Hydroelastic slamming[J].Journal ofMarine Science and Technology,2000,5(2):49-65.

[3]卢炽华,何友声.二维弹性结构入水冲击过程中的流固耦合效应[J].力学学报,2000,32(2):129-140. Lu Chihua,He Yousheng.Coupled analysis of nonlinear interaction between fluid and structure during impact[J].Journal of Theoretical and Applied Mechanics,2000,32(2):129-140.(in Chinese)

[4]Sun H,Faltinsen O M.Water impact of horizontal circular cylinders and cylindrical shells[J].Applied Ocean Research, 2006,28(5):299-311.

[5]Korobkin A,Gueret R,MalenicaŠ.Hydroelastic coupling of beam finite elementmodelwith Wagner theory ofwater impact [J].Journal of Fluids and Structures,2006,22(4):493-504.

[6]Wagner H.Über Stoß-und Gleitvorgängean der Oberflüche von Flüssigkeiten[J].ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik,1932,12(4):193-215.

[7]Peseux B,Gornet L,Donguy B.Hydrodynamic impact:Numerical and experimental investigations[J].Journal of Fluids and Structures,2005,21(3):277-303.

[8]Stenius I,Rosn A,Kuttenkeuler J.Explicit FE-modeling of fluid-structure interaction in hull-water impacts[J].International Shipbuilding Progress,2006,53:1031-121.

[9]Stenius I,Rosén A,Kuttenkeuler J.Explicit FE-modelling of hydroelasticity in panel-water impacts[J].International Shipbuilding Progress,2007,54(2):111-127.

[10]Aquelet N,Souli M,Olovsson L.Euler-Lagrange coupling with damping effects:Application to slamming problems[J]. Computer Methods in Applied Mechanics and Engineering,2006,195(1):110-132.

[11]Luo H B,Wang S,Guedes Soares C.Numerical prediction of slamming loads on rigid wedge for water entry problem by an explicit finite elementmethod[M].Advances in Marine Structures,GuedesSoares C,and FrickeW(Eds),Taylor&Francis, UK,2011.

[12]Luo H,Wang H,Soares C G.Comparative study of hydroelastic impact for one free-drop wedge with stiffened panels by experimental and explicit finite elementmethods[C]//ASME 2011 30th International Conference on Ocean,Offshore and Arctic Engineering.American Society ofMechanical Engineers,2011:119-127.

[13]骆寒冰,吴景健,王 珊,徐慧.基于显式有限元方法的二维楔形刚体入水砰击载荷并行计算预报[J].船舶力学, 2012,16(8):907-914. Luo Hanbing,Wu Jingjian,Wang Shan,XüHui.Parallel computing simulation ofwater entry of a 2D rigid wedge using an explicit finite elementmethod[J].Journal of Ship Mechanics,2012,16(8):907-914.(in Chinese)

[14]骆寒冰,刘 鑫,董德龙,赵中榜,季红叶,林维学.铝制加筋板楔形体入水砰击模型试验研究[J].水动力学研究与进展,2014,29(4):460-468. Luo Hanbing,Liu Xin,Dong Delong,Zhao Zhongbang,Ji Hongye,Lin Weixue.Experimental investigation ofwater impact of one free-drop wedge with stiffened aluminum panels[J].Journal of Hydrodynamics,2014,29(4):460-468.(in Chinese)

[15]李裕春,时党勇,赵 远.ANSYS 11.0、LS-DYNA基础理论与工程实践[M].中国水利水电出版社,2008. Li Yuchun,Shi Dangyong,Zhao Yuan.ANSYS 11.0,LS-DYNA basic theory and engineering practice[M].China Water-Power Press,2008.(in Chinese)

[16]LS-DYNA,Keyword User’s Manual,Livermore Software Technology Corporation[M].Version 971/Rev5,May 2001.

Numerical investigation of hydroelastic impact on one free-drop wedgew ith alum inum stiffened panels considering roll angles using ALE algorithm

LUO Han-binga,b,DONG De-longb,JIHong-yeb,ZHAO Zhong-bangb,GAO Yuanb
(a.State Key Laboratory of Hydraulic Engineering Simulation and Safety;b.Departmentof Naval Architecture and Ocean Engineering,Tianjin University,Tianjin 300072,China)

The explicit finite elementmethod using the Arbitrary Lagrangian-Eulerian(ALE)algorithm is applied to investigate the hydroelastic impact of one free-drop wedge with aluminum stiffened panels.The dead-rise angle is 20 degrees.The stiffened panel on each side of the wedge ismade up of 3 longitudinal stiffeners and 2 transverse frameswith different sizes of cross sections.The acceleration motion,stress responses on longitudinal stiffeners and transversewebs of the stiffened panels are obtained.The numerical results are validated with the new experimental results from drop testswith and without roll angles.This solution shows the capability of ALE algorithms and its potential to predict the hydroelastic slamming of local structures on ships.

ALE algorithm;aluminum stiffened panels;hydroelastic impact;roll angle;numerical simulation

U661

：Adoi:10.3969/j.issn.1007-7294.2017.02.007

2016-05-28

国家自然科学基金资助项目（51109159）

骆寒冰（1976-），男，副教授，E-mail:luohanbing@tju.edu.cn；董德龙（1988-），男，工程师。

1007-7294（2017）02-0175-09