以知识为载体 渗透数学思想
2017-05-03陈枝仙
陈枝仙

摘要:在数学课堂教学中,我们教授学生的不仅仅在于数学知识本身,而是数学知识中所蕴含的数学思想方法;数学教学的目的不仅是要关注学生掌握数学知识的情况,更要关注学生掌握和运用数学思想方法来解决实际问题的能力。
关键词:知识;渗透;数学思想
中图分类号:G633.6 文献标识码:A 文章编号:1992-7711(2017)02-0096
2016年衢州市柯城区初中数学“优秀教育人才携手新教师共成长展示活动”中,有新教师提出了我们数学课堂到底应该教给学生哪些知识,很多数学知识学生学了若干年后可能就忘了,而且生活中根本用不到二次函数、三角函数等知识,有必要学习吗?由此,引发笔者思考:我们的数学课堂到底应该教给学生什么?
《数学课程标准(2011年版)》将数学建模新增为核心概念之一,同时指出,建模思想需要在教学中逐步渗透,要引导学生不断感悟。那么,除建模思想外数学中还有常见的数形结合思想、分类讨论思想、从特殊到一般的转化思想、化归思想、类比思想等。在数学课堂教学中,我们教授学生的不仅仅在于数学知识本身,而是数学知识中所蕴含的数学思想方法;数学教学的目的不仅是要关注学生掌握数学知识的情况,还要关注学生掌握和运用数学思想方法解决实际问题的能力。日本数学教育家米山国藏说:“即使学生把所教的知识(概念、定理、法则和公式等)全忘了,铭记在他心中的数学精神、思想和方法却能使他终身受益。因此,数学思想是数学的灵魂。
现以一堂《3.1认识不等式》的新课教学过程为例,谈一些粗浅的想法。
一、创设情境,探究新知——渗透建模思想、数学符号思想、转化思想
(浙教版书本P90)合作学习:下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示:
1. 图3-1是公路上对汽车的限速标志,表示汽车在该路段行驶的速度不得超过40km/h。用v(km/h)表示汽车的速度,怎样表示v和40之间的关系?
2. 据科学家测定,太阳表面的温度不低于6000℃。设太阳表面的温度为t(℃g),怎样表示t与6000之间的关系?
3. 如图3-2,天平左盘放3个乒乓球,右盘放5g砝码,天平倾斜。设每个乒乓球的质量为x(g),怎样表示x(g)与5之间的关系?
4. 如图3-3,小聪与小明玩跷跷板。两人都不用力时,跷跷板左低、右高。小聪的身体质量为p(kg),书包的质量为2kg,小明的身体质量为q(kg),怎样表示p,q之间的关系?
5. 要使代数式有意义,x的值与3之间有什么关系?
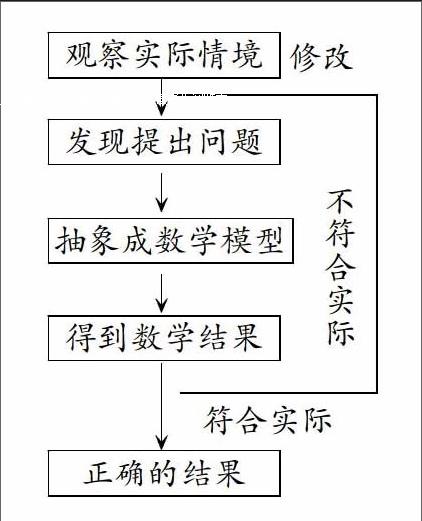
“合作学习”的目的是让学生经历不等式概念的产生过程,体验不等式是由于表示不等关系的需要而产生的数学模型,体现了建模思想。这个过程可以用如图所示的框图来体现:
数学符号表示是数学语言的重要特色,它能使数学研究对象更加准确、具体、形象,能够简明地表示事物的本质特征和规律。同时,它具有培养人们高度抽象思维的能力。在列不等式的过程中把文字表达转化为数学符号表示,既渗透了数学符号思想,又渗透了从文字到符号的转化思想。这些思想方法在今后学习几何知识时,用简洁的符号语言来表示性质、定理、判定等尤为重要。在生活中也常用符号语言帮助我们理解和记忆。
二、观察比较,归纳新知——渗透类比思想、归纳思想、抽象思想
观察列出的关系式:h1>h2,q 通过让学生比较所列出的这些不等式与已学过的等式相比较,找出所列不等式的共同特征,归纳不等式的概念。其中,将这些不等式与已学过的等式比较,让学生经历这个过程时,体会类比思想,使新知识实现正迁移。借助类比,还可以引导学生揭示隐藏于概念中的关键词,抽象概括出不等式的概念,从而更深刻地理解概念的本质。利用“有形”的知识(概念、性质等知识教材中写着,是显性的),渗透“无形”的思想(数学思想隐含在数学的知识体系中,是隐性的),提高学生的抽象和归纳能力。 三、理解概念,运用新知——渗透数学符号思想、转化思想、分类讨论思想 例1. 根据下列数量关系列不等式: (1)a是正数; (2)y的2倍与6的和比1小; (3)x2减去10不大于10; (4)设a,b,c为一个三角形的三条边长,两边之和大于第三边。 为了及时巩固不等式的概念,进一步识别不等式。让学生先独立完成这几个问题。要求学生找出可以转化为不等号的关键词;特别是第4小题,学生易列一个不等式,教师要引导学生从原题中找关键词,理解为什么要分类。在这一环节中,不仅是为了指导学生有效地运用数学知识、探尋解题的方向,更是对培养人的思维素质有特殊不可替代的意义。学生做例题,不仅对已经掌握的数学知识以及数学思想方法起到巩固和深化的作用,而且还会从中归纳和提炼出新的数学思想方法。这里仍将文字语言转换为数学的符号语言,继续渗透数学符号思想、转化思想,从而也体现了思想渗透过程中的反复性。第(4)小题要分类讨论列式,渗透了分类思想,也培养了学生严密的逻辑思维能力。 四、合作探究,再学新知——渗透数形结合思想、集合思想、转化思想 做一做: 1. 已知x1=1,x2=-2,请在数轴上表示出x1,x2的位置 2. x<1表示怎样的数的全体?如何在数轴上表示呢? 3. x≥-2表示怎样的数的全体? 4. 2≤x<1又表示怎样的数的全体? 利用第1题,回顾怎样在数轴上表示数,后面3题让学生合作探究如何把这样的数的全体在数轴上表示出来,表示过程中要注意哪些问题。学生在解决这几个问题时,需要借助数轴表示,利用图形帮助学生正确理解数量关系,促进学生形象思维和抽象思维的协调发展,沟通数学知识之间的联系,从数量关系中凸显最本质的特征。因此,学生在这个过程中体会到数形结合思想,把x<1,x≥-2,-2≤x<1表示到数轴上时,它们所表示的是一个范围,这里可渗透集合思想。
学生按照例题示范的程序与格式解答和例题相同类型的习题,实际上是数学思想方法的机械应用。此时,并不能肯定学生已经领会了所用的数学思想方法,只当学生将它用于新的情景,解决其他相关的问题并有创意时,才能肯定学生对这一教学本质、数学规律有了深刻的认识。例如,在解决了做一做的四个问题后,把x<1,x≥-2,-2≤x<1的数字换成字母,变式为x 五、实际应用题,再用新知——渗透数形结合思想,建模思想 例2. 一座小水电站的水库水位在12~20m(包括12m,20m)时,发电机能正常工作。设水库水位为x(m)。 1. 用不等式表示发电机正常工作的水位范围,并把它表示在数轴上; 2. 当水位在下列位置时,发电机能正常工作吗?①x1=8;②x2=10;③x3=15;④x4=19。 请用不等式和数轴给出解释。 教学中的重难点往往需要借助数学思想方法。教师要掌握重点、突破难点,更要有意识地运用数学思想方法组织教学。 在此例中,向学生提供了实际背景材料,可采用问题情境建立模型。通过对1,2两问的问题情境的研究为有效切入点,借助数轴展示,使学生的思维和经验全部投入到接受问题、分析问题和感悟思想方法的挑戰中,并再次体会建模思想,然后利用数学结合思想解释,以此来突破难点。这也符合学生认知发展规律和知识的延伸。让学生进一步体会到知识来源于生活,运用于生活,与新课的引入相呼应。 六、回顾反思,整合新知 让学生回顾反思本节课所学知识,教师再补充。在总结思想方法时,可结合具体知识,以知识为载体,不直接点明所运用的数学思想方法,而是着意引导学生领会蕴涵在其中的数学思想和方法,使他们在潜移默化中达到理解和掌握。使数学思想方法成为学生良好的认知结构的纽带,知识转化为能力的桥梁。 综上所述,数学思想是对数学知识发生过程的提炼、抽象、概括和升华,是对数学规律的理性认识。它直接支配数学的实践活动,是解决数学问题的灵魂。我们在课堂教学中要有意识地渗透数学思想,充分挖掘教材中蕴含的数学思想。在渗透数学思想的过程中要注意长期性和反复性,最终使数学思想内化为能为学生思考问题、解决实际问题提高积极效应。德国学者冯·劳厄指出:“教育无非是一切已学过的东西都忘掉时所剩下的东西”。总之,我们应当注重这种数学智慧的培养,使学生掌握数学思想方法,体会数学奥妙,为学生的创新能力打好基础。将来走上社会,能用数学思维解决碰到的各种实际问题。 参考文献: [1] 罗全民,金换换.跨界思维:基于“问题解决”理念的数学教学思考[J].初中数学教与学,2016(8). (作者单位:浙江省衢州市柯城区书院中学 324000)
