计及需求响应的Elman-NN短期负荷预测模型研究

于道林， 张智晟， 韩少晓， 李 晨

(1. 青岛大学自动化与电气工程学院， 山东 青岛 266071； 2. 山东省电力公司， 山东 济南 250001；3. 国家电网公司电力调度控制中心， 北京 100031)

计及需求响应的Elman-NN短期负荷预测模型研究

于道林1， 张智晟1， 韩少晓2， 李 晨3

(1. 青岛大学自动化与电气工程学院， 山东 青岛 266071； 2. 山东省电力公司， 山东 济南 250001；3. 国家电网公司电力调度控制中心， 北京 100031)

通过频谱分析研究了需求响应负荷的基本特性，并以此为依据建立了计及需求响应的Elman神经网络(Elman-NN)预测模型。Elman-NN具有处理动态信息能力强、训练时间短、全局寻优性强的优点。通过实际算例，对比在Elman-NN模型中计及需求响应因素前后的预测性能，结果显示计及需求响应因素可显著提高Elman-NN模型预测精度。本文证实了在模型中计及需求响应因素的重要作用，为需求响应负荷的预测研究奠定了必要的理论基础。

需求响应； 负荷特性； Elman神经网络； 短期负荷预测

1 引言

传统电力体制下，通常认为需求侧负荷是“刚性”不可控的，电能可保持供需平衡，只是发电机组单方面对需求侧电能变化的响应。随着电力市场日益成熟，用户负荷呈现出一定的需求弹性，这意味着可通过技术手段改善用户负荷曲线。所谓需求响应(Demand Response，DR)[1]，是指用户在电价机制或激励机制的引导下，为获取经济利益而改变正常用电习惯的行为。需求响应可以使需求侧资源同样被纳入调度范畴，提高客户端用电效率，综合优化整个电力系统的能源配置。欧美很多国家已经成功实施多个需求响应项目[2]，实施结果表明需求响应可有效缓解系统短期容量不足，推迟电网升级，节省新建发电设备和输电设施所需的额外成本，提高系统稳定性[3]。相对于欧美等发达国家，我国对需求响应的研究起步较晚，无论是其自动化还是标准化都处于初步阶段，但智能电网为需求响应提供了技术支持[4，5]。智能电网的高级量测系统能够在电网与用户之间建立双向通信通道，为系统调度员(Distribution System Operators，DSOs)进行短期负荷预测提供重要的参考信息。文献[6]综合考虑分时电价和可中断负荷对发电调度的影响，建立了智能电网下计及用户侧互动的发电调度计划模型。文献[7]在传统预测方法上进行参数修正，基于多元线性回归法建立了直接法，用于预测考虑需求侧管理量的负荷。文献[8]考虑需求响应提供虚拟出力和虚拟备用的双重功能，采用基于场景概率的两阶段随机模型，建立了含风电电力系统的供需侧联合调度模型。

目前国内对需求响应的研究主要集中于不确定性因素的建模，以及对原始负荷曲线的影响，很少涉及计及需求响应的负荷预测问题。需求响应会使用户负荷曲线产生变化，需要在传统预测方法基础上做出调整或改进，以提高电力系统短期负荷预测精度。基于此，本文分析了需求响应机理，通过频谱分析研究计及需求响应负荷的特性，并以此为依据构建了计及需求响应的Elman神经网络(Elman-Neural Networks，Elman-NN)短期负荷预测模型。结合某地区实际负荷数据进行试验，并与传统BP-NN预测模型进行对比，结果证明本文预测模型具有一定的实用价值。

2 计及需求响应负荷的特性分析

2.1 需求响应机理

在系统负荷超过系统能够获得的最大电力供应时，可通过发送需求响应信号DR，减少可控负荷，降低供电压力。DR信号既可由系统调度员发送给工业等大型用户，也可由负荷聚合商(Load Aggregator，LA)发送给居民等小型用户。DR信号必须符合实际情况，其作用下期望需求响应曲线的幅值大小和持续时间都应受到约束限制。由于需求响应的灵活性，可控负荷在结束被控制并重新接入系统时，被滞后的负荷将出现负荷反弹现象[9]。本文以负荷曲线的形式协助描述需求响应机理[10]，DR信号作用下的期望需求响应曲线如图1所示。

图1 期望需求响应曲线Fig.1 Profile of expected demand response

图1中，V1表示期望需求响应曲线的幅值；t1表示期望需求响应持续时间，即DR信号持续时间；t2表示滞后负荷反弹持续时间。

2.2 用户实际需求响应模型

我国对自动需求响应的研究目前还处于初步阶段[11]，用户完全按照自己意愿签订协议并参与需求响应项目，而且小型用户的需求响应随机性较强，因此，用户实际需求响应与期望需求响应之间存在一定差异：

(1) 用户实际需求响应较DR信号存在延时。

(2) 需求响应的灵活性导致需求响应结束后产生的负荷反弹不确定。

(3) 无法保证所有签订协议的用户均能够严格做出准确需求响应。

同时，用户实际需求响应会受到日期、时刻、天气和电价等外界因素的影响，处于时变状态。综合考虑上述因素，本文构建了基于时变函数的用户实际需求响应模型，如式(1)所示。

(1)

式中，dr1表示用户实际需求响应曲线数值；dr表示期望需求响应曲线数值；n为一天中负荷采样点的编号，n=0,1,…,95；v为分布均匀的零均值独立成分，模拟用户随机性；nb表示含dr的项数；wn表示模拟在第n个负荷采样点处影响用户实际需求响应的外界不确定性因素，由于本文研究的是电力系统短期负荷预测，因此对wn做了简化处理，只反映出时刻因素，其数值等于负荷采样点n所属的小时编号，即wn=0,1,…,23；i=0,1,…,nb-1，为bi(wn-i)的编号；bi(wn-i)为关于w的多项式函数，用于定量表征w对用户实际需求响应的影响，如式(2)所示。

(2)

式中，bi，j(j=1,2,…,p)是常数，表示每项的系数；p为βj(wn)的项数；βj(wn)为wn的给定函数，如式(3)所示。

(3)

wn能够简单量化时刻因素对用户需求响应程度的影响，而该影响通过βj(wn)实现。式(3)可使用户白天需求响应的程度大于晚上，与生活实际情况相符。

用户实际需求响应模型中融入了DR信号作用的累积效应，同时简单地考虑了外界因素影响，以及用户行为的随机性，满足用户实际需求响应与期望需求响应的差异性特征。

2.3 计及需求响应负荷的特性分析

研究负荷特性时，可通过频谱分析了解电力系统负荷周期性变化规律，更好地识别和挖掘负荷特性[12]。快速傅立叶变换(Fast Fourier Transformation, FFT)属于离散傅立叶变换(Discrete Fourier Transformation, DFT)的一种，DFT及其逆变换公式分别如下：

(4)

(5)

式中，k为频域样本点的序列号；n为时域样本点的序列号；Xd(k)为时域样本集第k个值对应的频域值；x(n)为时域样本集中的第n个值；N为样本集中数值的个数。

与一般DFT相比，FFT运算量大大减少，计算速度快，能够有效识别负荷曲线的频谱特性，结合MATLAB编程仿真可用于协助分析计及需求响应负荷的特性[13]。

以上述理论为依据，结合某地区电网2008年实际负荷数据进行需求响应试验。需求响应机理下期望需求响应曲线幅值V1∈[300,800]MW，持续时间t1∈[1,4]h。负荷反弹幅值为期望需求响应幅值的0.3倍，负荷反弹持续时间t2=0.3t1。用户实际需求响应模型参数设定：式(1)中，dr项的数量nb=3，分布均匀的零均值独立成分v的标准差设置为5；式(2)中，βj(wn)的项数p=1，各项系数b0,0=0.30，b0,1=0.02，b1,0=0.15，b1,1=0.01，b2,0=0.05，b2,1=0.01。相邻两个DR信号之间的时间间隔位于[12h,72h]区间范围内。利用FFT对计及需求响应负荷进行频谱分析，MATLAB仿真运行结果图像如图2所示。

图2 频谱分析仿真图像Fig.2 Simulation results of spectrum analysis

将程序频谱分析结果转变为负荷特性频谱图像，幅值较小的谱分量忽略不计。负荷特性频谱图像如图3所示。

图3 计及需求响应负荷的特征频谱Fig.3 Characteristic spectrum of load considering DR

由图3可以看出，以24h(即一天)为周期的谱分量幅值最大，而且远大于其他周期对应谱分量的幅值。这表明，计及需求响应负荷数据与原始负荷数据主要负荷特性相同，相邻日期相同时刻的负荷数值表现出最高的相关性。

本文将需求响应因素作为外界因素处理，负荷特性分析结果将对预测模型输入量的组成起到决策性作用。

3 计及需求响应的Elman-NN预测模型

3.1 Elman神经网络结构

Elman-NN是一种典型的动态递归神经网络[14，15]，通常包含四层：输入层、隐含层、承接层和输出层，其网络结构如图4所示。除去承接层剩下的部分相当于前馈网络，输入层神经元用于传输信号，输出层神经元起到线性加权作用。

图4 Elman-NN预测模型结构图Fig.4 Structure of Elman-NN forecasting model

Elman-NN的特点是隐含层的输出通过承接层的延迟与存储之后，再自联到隐含层的输入，承接层可视为一步延时的算子。这种自联方式相当于在基本BP网络基础上增加了内部反馈网络，使其对历史状态的数据具有敏感性，具备了适应时变特性的能力，从而达到了动态建模的目的。

3.2 Elman神经网络学习过程

图4中，k表示时刻；u，x，xc和y分别表示m维输入向量，n维隐含层结点单元向量，n维反馈状态向量和p维输出向量，此处p为1；ω1，ω2，ω3分别表示输入层连接隐含层、承接层连接隐含层和隐含层连接输出层的权值。则Elman网络的非线性状态空间表达式可如式(6)表示。

(6)

式中，g(·)为输出层神经元的传递函数；f(·)为中间层(隐含层和承接层)神经元的传递函数。由式(6)可进一步推导出式(7)。

(7)

式中，xc(k-1)=x(k-2)，由此，xc(k)可不断依次递推，并且依赖于每次推导中不同时刻的连接权值，属于动态递推过程。Elman-NN进行权值修正时采用BP算法，训练指标由误差平方和函数确定，如式(8)所示。

(8)

3.3 计及需求响应的Elman-NN预测模型建模

需求响应项目会使用户日负荷曲线产生变化，必须在传统预测方法基础上做出调整或改进，以提高预测精度。通过1.3节中对计及需求响应负荷的特性分析，确定计及需求响应Elman-NN预测模型输入量的历史负荷数据和影响因素组成，如式(9)所示。

(9)

式中，u表示Elman-NN预测模型的输入量；k表示要预测的负荷采样点的时间序列编号，k=0,1,…,95；d表示要预测的负荷采样点所在的天数编号；h表示历史负荷数据向量，如式(10)所示；w表示温度、天气和日类型(工作日或休息日)等外在影响因素向量，如式(11)所示；dr1表示需求响应因素向量，如式(12)所示。

(10)

(11)

(12)

本文定义了一种新的向量表示方式“[A·]”，其中“A·”表示对元素的按序列举。例如：

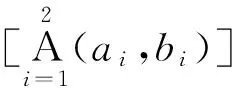
式(10)中，h表示9维历史负荷数据向量，load1表示计及需求响应的负荷数据。式(11)中，w表示17维外在影响因素向量，Tmax、Tave、Tmin和s分别表示某日的最高温度、平均温度、最低温度和天气影响因子，g表示预测日的日类型影响因子。式(12)中，dr1表示9维需求响应因素向量，dr1表示用户实际需求响应曲线数值。另外，i和j均用作计数编号。综上，u为Elman-NN预测模型的35维输入量。为进一步验证预测模型中计及需求响应因素的重要性，本文将预测模型中计及和不计及需求响应因素时的预测结果进行对比，具体工作流程如图5所示。

图5 两种模型对比流程图Fig.5 Flowchart of comparision of two models

4 算例分析

4.1 影响因素数据预处理

对于计及需求响应的负荷数据，影响其负荷特性的因素包括温度、天气状况和DR信号等，它们的量纲不同，值域差异较大。为避免部分负荷影响因素在总体映射效果中被歪曲甚至淹没，同时防止神经元在神经网络训练和学习过程中饱和，需要在模型训练之前对各种负荷影响因素统一进行标准化预处理。

日类型数据：工作日影响因子取值为1，休息日影响因子取值为0.5。

天气类型数据：晴天、多云(含阴天)和雨雪天气的影响因子分别取值1、0.5和0。

对于温度，由于其数值在有限范围内波动，可以同负荷一样采取归一化处理，处理方法如式(13)所示。

(13)

对每个DR信号作用下的期望需求响应曲线数值须以整体负荷为基准作特殊标准化处理，如式(14)所示。

(14)

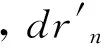
4.2 算例结果分析

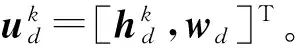
BP-NN预测模型参数设定：隐含层节点数取12，学习速率取0.02，动量因子取0.9，最大训练次数取20000，目标误差取0.005。Elman-NN预测模型参数设定：中间层神经元数目取12，中间层传递函数选用tansig函数，输出层传递函数选用purelin函数，利用函数train调用traingdx训练网络，训练步数设定为20000，目标误差取0.001。

4.2.1 不计及需求响应时模型预测性能比较

随机选取该电网某日负荷进行预测，预测日的9～20h时段属于其峰负荷时段。采用电价政策，提升预测日12～14h时间段内的电价，并于日前作为DR信号发送给用户，通过电价差引导用户降低预测日该时段负荷。不计及需求响应因素时，分别使用Elman-NN模型和BP-NN模型对该地区电网同一天负荷进行预测，预测结果对比如图6所示。

图6 不计及需求响应时预测结果对比Fig.6 Comparison of prediction results without DR

由图6可以看出：在12～14h时间段内，真实负荷曲线因受DR信号影响明显凹陷；在14～15h时段内，真实负荷曲线由于滞后负荷反弹，曲线明显凸出；由于DR信号的作用随时间递减，且具有一定延时性，式(1)中dr项数nb取值为3，即每个时点负荷受该时点及前两个时点处DR信号累积影响，同时，由式(3)，12h之后外界不确定性因素影响减弱，因此15h之后DR信号作用逐渐减小，真实负荷曲线形态无明显凹凸变化；Elman-NN模型和BP-NN模型的负荷预测曲线在12～15h时段内均未出现明显凹凸变化特征。这表明在不计及需求响应因素时，两种模型均无法预测出真实负荷曲线因受DR信号影响而产生的变化。因此，需要对原有负荷预测模型做出调整或改进，以提高预测需求响应负荷时的预测精度。

4.2.2 计及需求响应时模型预测性能比较

受DR信号影响，原始负荷曲线在波形上会出现突然凸出或者凹陷的情况，这种特殊性增加了需求响应负荷的预测难度，本文将需求响应因素作为外界因素处理，见式(9)。在模型中计及需求响应因素的情况下，分别使用Elman-NN模型和BP-NN模型对该地区电网同一天负荷进行预测。为保证每种模型预测过程的公平性，固定DR信号发送时刻、幅值及持续时间，确保两种模型使用的负荷数据相同。预测结果对比如图7所示。

图7 计及需求响应时预测结果对比Fig.7 Comparison of prediction results with DR

由图7可看出，计及需求响应因素时，Elman-NN模型和BP-NN模型都能够成功预测出12～15h时间段内负荷曲线因受DR信号影响而产生的变化，这与图6预测结果形成鲜明对比，表明在模型中计及需求响应因素对提高需求响应项目的预测精度非常重要。不计及和计及需求响应因素时，Elman-NN模型和BP-NN模型预测结果误差指标对比如表1所示。

表1 两种情况下模型预测结果对比Tab.1 Comparision of forecasting results of models in two different situations

注：EMAPE为平均绝对百分误差；EMAX为最大相对误差。

由表1可知，在预测模型中计及需求响应因素后，Elman-NN模型和BP-NN模型的MAPE指标分别下降5.972%和6.847%，预测性能得到显著改善。

为了进一步验证计及需求响应Elman-NN短期负荷预测模型的优越性和泛化能力，在模型中计及需求响应的情况下，分别采用Elman-NN和BP-NN两种模型对该地区电网同一周进行负荷预测，两种模型的预测结果和误差比较如表2所示。

表2 计及需求响应的模型预测结果对比
Tab.2 Comparision of forecasting results of models with DR

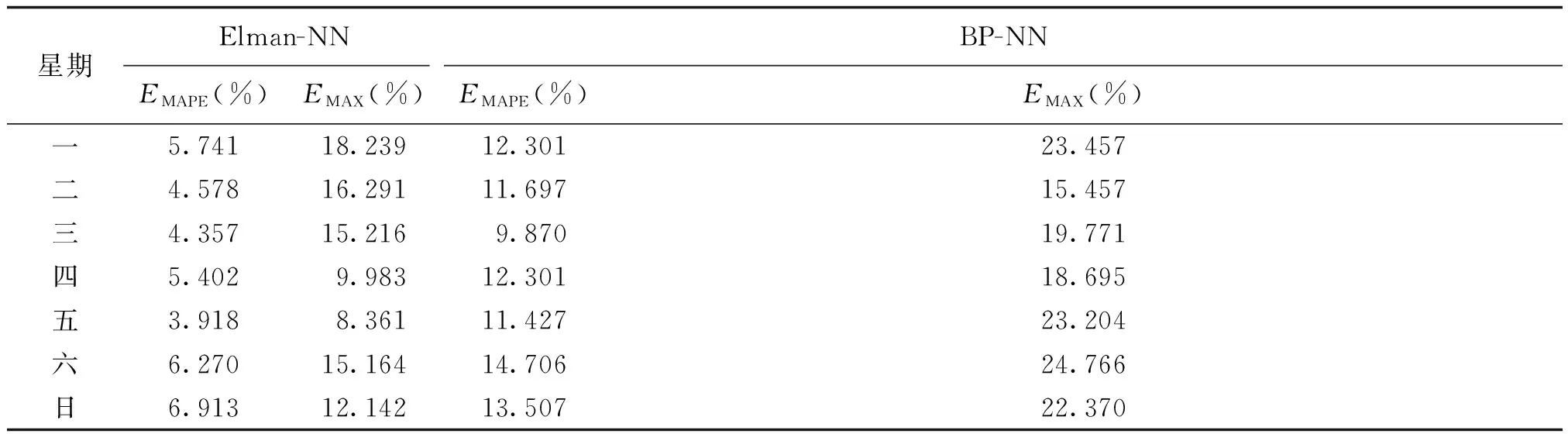
星期Elman-NNBP-NNEMAPE(%)EMAX(%)EMAPE(%)EMAX(%)一5.74118.23912.30123.457二4.57816.29111.69715.457三4.35715.2169.87019.771四5.4029.98312.30118.695五3.9188.36111.42723.204六6.27015.16414.70624.766日6.91312.14213.50722.370

注：EMAPE为平均绝对百分误差；EMAX为最大相对误差。

由表2可知，计及需求响应因素后，Elman-NN模型和BP-NN模型的预测精度都得到显著提高，而且Elman-NN模型比BP-NN模型的MAPE指标低6.947%，表现出更好的预测性能和稳定性。这表明，计及需求响应的Elman-NN模型对需求响应项目具有较好的实用性。

5 结论

本文分析了需求响应机理，构建了基于时变函数的用户实际需求响应模型。使用FFT对计及需求响应负荷数据进行频谱分析，识别其基本负荷特性，并以此为依据构建了计及需求响应的Elman-NN短期负荷预测模型。通过实际算例仿真，证明Elman-NN模型预测性能明显优于传统BP-NN模型，且在模型中计及需求响应因素可有效预测DR信号对日负荷曲线的影响，显著提高模型预测精度。本文并未对影响需求响应的各项不确定性因素分类模块化，这将成为下一步研究的主要方向。

[1] 张钦, 王锡凡, 王建学, 等 (Zhang Qin, Wang Xifan, Wang Jianxue, et al.). 电力市场下需求响应研究 (Survey of demand response research in deregulated electricity markets) [J]. 电力系统自动化 (Automation of Electric Power Systems), 2008, 32(3): 97-106.

[2] 潘小辉, 王蓓蓓, 李扬, 等 (Pan Xiaohui, Wang Beibei, Li Yang, et al.). 国外需求响应技术及项目实践 (Demand response technology abroad and its practice) [J]. 电力需求侧管理 (Power Demand Side Management), 2013, 15(1): 58-62.

[3] 田世明, 王蓓蓓, 张晶 (Tian Shiming, Wang Beibei, Zhang Jing). 智能电网条件下的需求响应关键技术 (Key technologies for demand response in smart grid) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2014, 34(22): 3576-3589.

[4] 赵雪霖, 何光宇, 杨文轩, 等 (Zhao Xuelin, He Guangyu, Yang Wenxuan, et al.). 智能用电网络的设计与初步实现 (Design and initial implementation of smart electric appliance network) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2014, 33(10): 52-57.

[5] 王蓓蓓 (Wang Beibei). 面向智能电网的用户需求响应特性和能力研究综述 (Research on consumers' response characterics and ability under smart grid: a literatures survey) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2014, 34(22): 3654-3663.

[6] 刘小聪, 王蓓蓓, 李扬, 等 (Liu Xiaocong, Wang Beibei, Li Yang, et al.). 智能电网下计及用户侧互动的发电日前调度计划模型 (Day-ahead generation scheduling model considering demand side interaction under smart grid paradigm) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2013, 33(1): 30-38.

[7] 苏卫华, 储琳琳, 张亮, 等 (Su Weihua, Chu Linlin, Zhang Liang, et al.). 考虑需求侧管理的负荷预测方法研究 (Study on load forecast method considering demand side management) [J]. 华东电力 (East China Electric Power), 2010, 38(8): 1236-1239.

[8] 杨丽君, 李健强, 李学平, 等 (Yang Lijun, Li Jianqiang, Li Xueping, et al.). 考虑需求响应的含风电电力系统日前经济调度 (Day-ahead dispatching for wind power integrated system considering demand response) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2015, 34(11): 29-36.

[9] 张钦, 王锡凡, 别朝红, 等 (Zhang Qin, Wang Xifan, Bie Zhaohong, et al.). 电力市场下直接负荷控制决策模型 (A decision model of direct load control in electricity markets) [J]. 电力系统自动化 (Automation of Electric Power Systems), 2010, 34(9): 23-28.

[10] Andrea Garulli, Simone Paoletti, Antonio Vicino. Models and Techniques for Electric Load Forecasting in the Presence of Demand Response [J]. IEEE Transactions on Control Systems Technology, 2014, 23(3): 1087-1097.

[11] 高赐威, 梁甜甜, 李慧星, 等 (Gao Ciwei, Liang Tiantian, Li Huixing, et al.). 开放式自动需求响应通信规范的发展和应用综述 (Development and application of open automated demand response) [J]. 电网技术 (Power System Technology), 2013, 37(3): 692-698.

[12] 张雪莹, 管霖, 谢锦标 (Zhang Xueying, Guan Lin, Xie Jinbiao, et al.). 采用谱分析建模和基于人工神经网络的短期负荷预测方案 (Short-term load forecasting based on artificial neural network and modeling with spectrum analysis) [J]. 电网技术 (Power System Technology), 2004, 28(11): 49-52.

[13] 陈大银 (Chen Dayin). Matlab软件在频谱分析中的应用 (Application of Matlab software in spectrum analysis) [J]. 贵阳学院学报 (Journal of Guiyang College), 2014, 9(2): 28-30.

[14] 刘远龙, 龚文杰, 徐超, 等 (Liu Yuanlong, Gong Wenjie, Xv Chao, et al.). 基于PSO-Elman神经网络的电力系统短期负荷预测模型研究 (Research of short-term load forecasting model based on PSO-Elman Neural Network) [J]. 青岛大学学报 (Journal of Qingdao University), 2010, 25(3): 43-47.

[15] 朱晟, 蒋传文, 侯志俭 (Zhu Sheng, Jiang Chuanwen, Hou Zhijian). 基于气象负荷因子的Elman神经网络短期负荷预测 (Application of a weather component based Elman Neural Network to short-term load forecasting) [J]. 电力系统及其自动化学报 (Proceedings of the CSU-EPSA), 2005, 17(1): 23-26.

Study of short-term load forecasting model based on Elman-NN considering demand response

YU Dao-lin1, ZHANG Zhi-sheng1, HAN Shao-xiao2, LI Chen3

(1. School of Automation and Electrical Engineering, Qingdao University, Qingdao 266071, China;2. Shandong Electric Power Company, Jinan 250001, China; 3. Electric Power Dispatching and Control Center, State Grid Company of China, Beijing 100031, China)

This paper studies the basic characteristics of the load which takes demand response into consideration through frequency spectrum analysis and constructs a load forecasting model based on Elman-Neural Networks (Elman-NN), which also takes demand response into account. Elman-NN is characterized by a short training period and its ability to deal with dynamic information and achieve the whole optimum. An actual case is used to compare the forecasting performance of the models based on Elman-NN with and without taking demand response into account. Results exhibit that considering demand response can markedly improve the forecasting accuracy of models based on Elman-NN. The paper confirms the significance of considering demand response in forecasting models and lays necessary theoretical foundation for the study of predicting load which takes demand response into account.

demand response; load characteristic; Elman-Neural Networks; short-term load forecasting

2016-06-21

国家自然科学基金项目 (51477078)

于道林(1991-), 男， 山东籍, 硕士研究生, 研究方向为电力系统短期负荷预测； 张智晟(1975-), 男， 山东籍, 教授, 博士后, 研究方向为电力系统经济负荷分配、 负荷预测和故障诊断、 配电网自动化(通讯作者)。

TM743

A

1003-3076(2017)04-0059-07