基于Matlab的电气传动控制系统课程教学研究

胡学芝

(湖北理工学院 电气与电子信息工程学院,湖北 黄石 435003)

基于Matlab的电气传动控制系统课程教学研究

胡学芝

(湖北理工学院 电气与电子信息工程学院,湖北 黄石 435003)

Matlab 具有强大的数学运算功能，而其仿真工具Simulink具有模块化、面向结构图编程及可视化等优点，因而Matlab在工程系统仿真中得到了广泛的应用。分别以直流调速系统中的双闭环直流调速系统和交流调速系统中的DTC系统为例，讨论了如何将Matlab/Simulink仿真应用于“电气传动控制系统”课程教学中，提出了一种将理论教学和仿真实验相结合的教学模式，通过在课程教学中应用和实施该教学模式，取得了良好的教学效果。

Matlab；仿真；教学模式；DTC；电气传动控制系统

0 引言

“电气传动控制系统”是电气工程及其自动化专业的一门主干专业课，它的主要内容包括直流调速和交流调速2个部分，同时它综合了电机学、电力电子技术、自动控制理论、计算机控制技术和微电子技术等多门学科知识，该课程具有知识面宽、理论抽象、与工程实践结合紧等特点[1]，且具有一定的难度和深度，学生学习时难以及时理解和掌握。建立系统的动态数学模型并展开分析是本课程的重要教学环节，而传统教学模式不能直观展现参数变化对系统性能的影响，学生学习兴趣不浓，学习效率低。为了提高教学质量并改善教学效果，本文提出了一种基于Matlab的将课堂教学、仿真实验和课程设计融为一体的交互式教学模式。该教学模式将课程的理论知识与系统设计及工程应用有效地结合起来，使学生在学习中能够清楚地看到系统控制模型及参数变化对系统动态及稳态性能的影响，同时也让学生掌握了系统的建模方法及要点，它将理论教学、仿真实践及系统设计与分析结合在一起，激发了学生的学习兴趣，提高了学习效率。

Matlab下的Simulink 工具是对各种动态系统进行建模和仿真的平台，它既提供基于控制系统模块库的面向传递函数的建模仿真方法，又提供了基于SimPower System 工具箱的面向控制系统电气原理图的建模仿真方法。这2种方法都是使用系统模型框图进行组态的仿真平台，用户可以用图形化的方法直接建立系统仿真模型，并通过Simulink环境中的菜单直接启动系统的仿真过程，同时将结果在示波器上显示出来[2]。本文为介绍上述2种仿真方法，在直流调速系统实例中应用面向传递函数的建模仿真方法，而DTC系统应用面向控制系统原理图的方法进行仿真。

1 基于Matlab的课程教学模式及实施过程

Simulink支持线性与非线性、连续与离散系统图形化的建模与仿真。通过Matlab中的Simulink工具箱可以方便地建立系统的构图模型，快速设置系统控制参数，并即时通过Simulink中的菜单启动仿真，根据仿真结果对系统参数进行修正和调整，直到最后得到满意结果为止。在课程教学中适时演示，让学生及时看到参数变化对系统性能的影响，能够增强学生对抽象理论环节知识的理解，提高学生的学习效率和学习兴趣。电气传动控制系统课程教学结构图如图1所示。由图1可以看出，该课程的教学过程包括以下几个环节。

1)引入课程内容并进行理论分析。根据教学计划引入课程教学内容,建立系统模型并进行理论分析，其中包括建立组成系统各环节的传函及其所涉及调节器的模型和参数设置，比如在单闭环直流调速系统分析中分别建立了电机环节、电力电子变换环节(包括2种变换器)、调节器和测速反馈等环节的传函，应用控制理论的方法(包括动态指标和稳态指标的计算方法)分析系统的动态性能。

2)引入Matlab/Simulink仿真并与理论分析结果进行比较。在引入典型系统时先进行理论分析，再及时完成仿真实验并验证结果。仿真过程分为2个步骤：①在理论分析过程中讲述控制系统调节器的不同算法时，通过仿真结果比较各算法的特点以及同一算法不同参数配合时的不同响应结果，如讲调节器的PI算法时，对不同Kp和Ki取值时响应曲线的变化情况进行仿真分析，重点观察在最佳PI参数时的响应曲线。②搭建系统子模块仿真图，将各子模块组成完整的系统仿真模型并进行仿真。仿真过程中，当改变调节器的参数时，可直观的看到系统响应曲线的变化，并验证与理论分析结果是否一致，如对双闭环不可逆直流调速系统进行仿真时，选用PI电流调节器和转速调节器并观察不同参数设置时系统的电流、转速波形，分析和对比在非最佳参数设置和最佳参数设置时启动过程的电流、转速的超调量和系统动态过程调节时间，使学生理解启动过程的3个阶段及2个调节器所处的不同状态(饱和与不饱和)。观察系统的稳态误差及抗干扰指标的不同。

3)实际工程系统的设计及仿真训练。人才培养方案中设有课程设计，在课程开始时就下达课程设计任务书，要求学生完成一个直流调速系统的设计和一个交流系统的建模和仿真任务。进行直流调速部分的设计及仿真时分3～4人为一组，每组成员所选方案不能相同，比如可选用可逆的系统和不可逆的系统， SCR-M和PWM-M系统，单闭环和双闭环系统；仿真时所选方案也不能相同，比如可选用面向系统传递函数的仿真方法或选用面向系统电气结构图的仿真方法完成仿真验证；最后要求学生答辩并提交设计报告。本课程教学通过与Matlab仿真结合，以及上述环节在课程教学中的应用和实施，培养了学生的创新精神和工程实践能力，提高了学生学习效率，为下一步完成毕业设计和以后的工作打下了良好的基础。

2 典型交、直流调速系统仿真案例及实施

交、直流调速系统实例有很多。本研究分别选用一个直流调速系统和一个交流调速系统中的典型系统进行建模与仿真，并分别应用面向传递函数的建模仿真和面向电气结构图的建模仿真完成仿真实例。

2.1 双闭环直流调速系统建模与仿真 选用双闭环直流调速系统进行建模与仿真，应用面向传递函数的建模与仿真完成仿真实例，该方法具有可视化的特点，其仿真模型即系统结构图，参数可在调用Continuous模块库时直接进行修改[3]。

首先在理论分析中通过工程设计法建立SCR-M转速电流双闭环直流调速系统结构。针对本系统的主要环节分别求出各环节的传递函数。本系统主要由给定环节、SCR触发整流环节、直流电动机(包括平波电抗器)、测速环节、转速调节器和电流调节器等环节组成。利用Simulink中Continuous模块库中的传递函数模块，建立以上环节的传递函数模型并设置参数，然后按照系统的动态结构图将各环节有机结合起来，并进行仿真实验。仿真过程分为如下2个步骤。

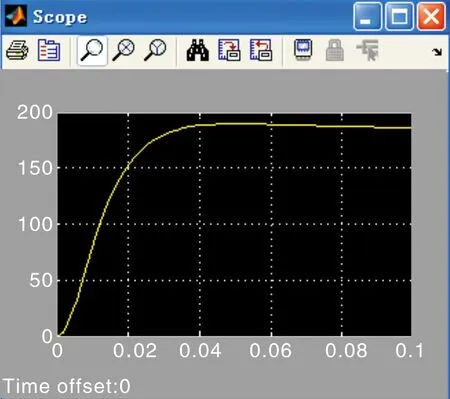
1)对内环-电流环进行仿真实验，电流环仿真模型如图2所示。饱和非线性模块(Saturation)的限幅值取为±10，选中Simulink窗口的Simulation→Configuration Parameters菜单项，将开始时间和结束时间分别设置为0.0 s和0.05 s，启动仿真，得出阶跃响应曲线，从响应曲线中可观察到PI参数的变化对系统响应指标值的影响，如取KT=0.25时，对应PI调节器的传递函数为0.5067+16.89/s，此时系统为过阻尼状态，响应时间较长，电流环过阻尼时的阶跃响应曲线如图3所示。取KT=0.5时，对应PI调节器的传递函数为1.013+33.77/s，此时对应于欠阻尼状态，并且是典Ⅰ最佳系统，电流环欠阻尼时的阶跃响应曲线如图4所示，此时响应曲线超调小且响应快；图2 和图4中稳态值较200 A略小点，说明电流调节器受电机反电动势的扰动，系统对阶跃扰动是有静差的。

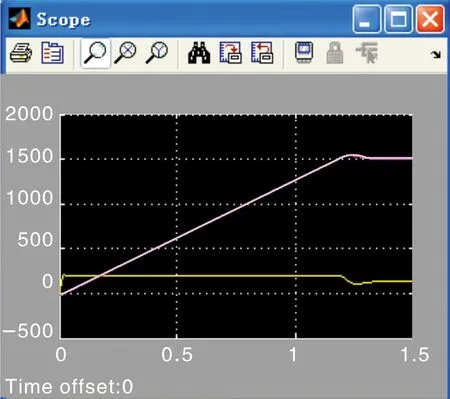
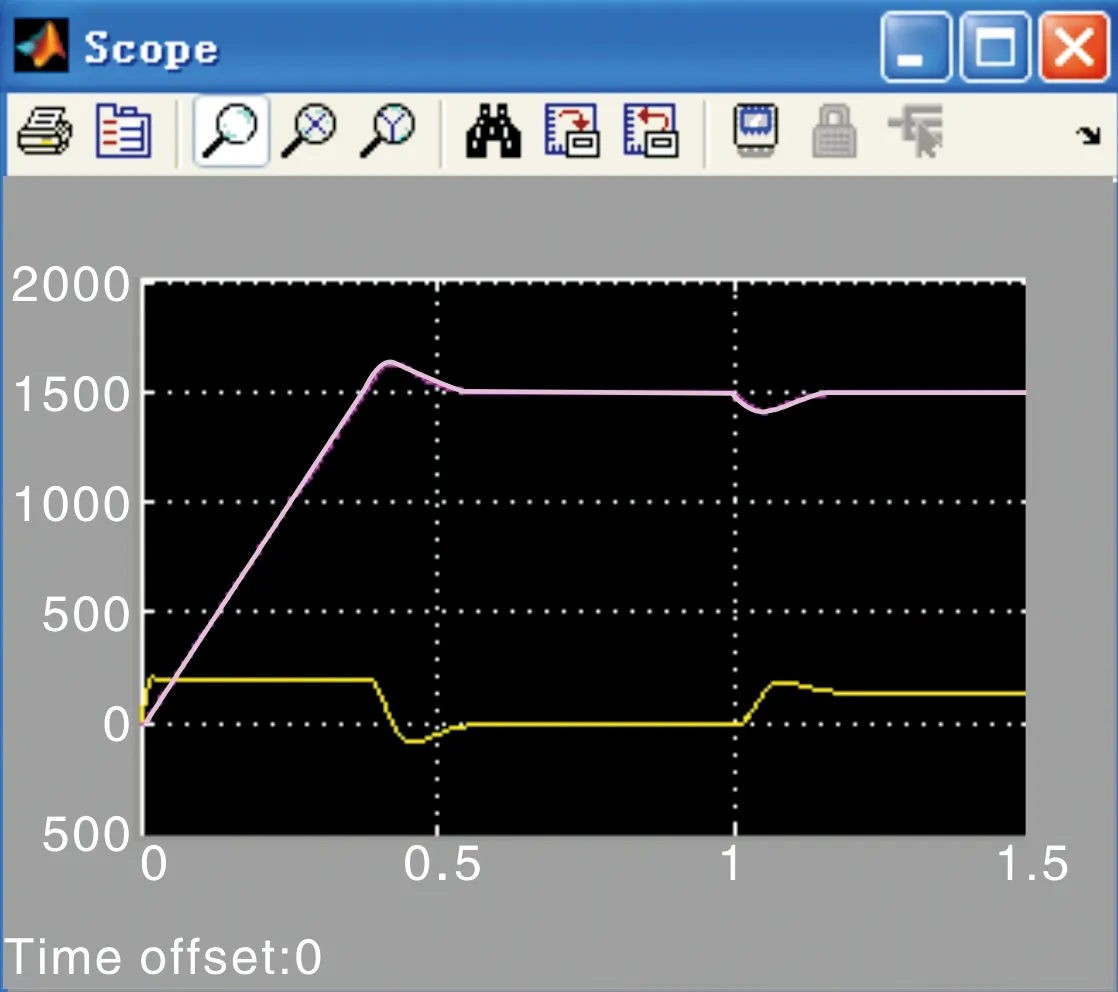
2)对外环-转速环进行仿真，转速调节器ASR也采用PI调节器，基于面向传递函数的转速电流双闭环系统仿真模型如图5所示。为了在示波器模块中显示出转速与电流之间的关系，在仿真模型的Signal Routing组中选用Mux模块将几个输入变量聚合成1个向量再输出给Scope，聚合模块对话框中的Number of inputs设置为2。根据工程设计法中外环按最佳典Ⅱ系统模型设置参数[4-5]，则转速环PI调节器的传函为11.7+134.48/s，阶跃值取10，根据系统给定值，负载电流设置为136 A，额定转速是1500 r/min。启动仿真，从仿真结果中可清楚地看到启动过程的3个阶段：电流上升、恒流升速和转速调节。在额定负载下启动得到的额定转速波形如图6所示。系统的抗干扰过程波形如图7所示，在图7所示的波形中，由系统空载启动进入稳定状态时突加额定负载的响应过程，可看出系统对阶跃扰动是无静差的。

在课程教学中，先应用工程设计法设计建模仿真方案，而工程设计法是在一定的近似条件下所得到，因此在仿真时可根据仿真结果对设计的参数实时进行修正和调整，直到最后达到满意的结果。

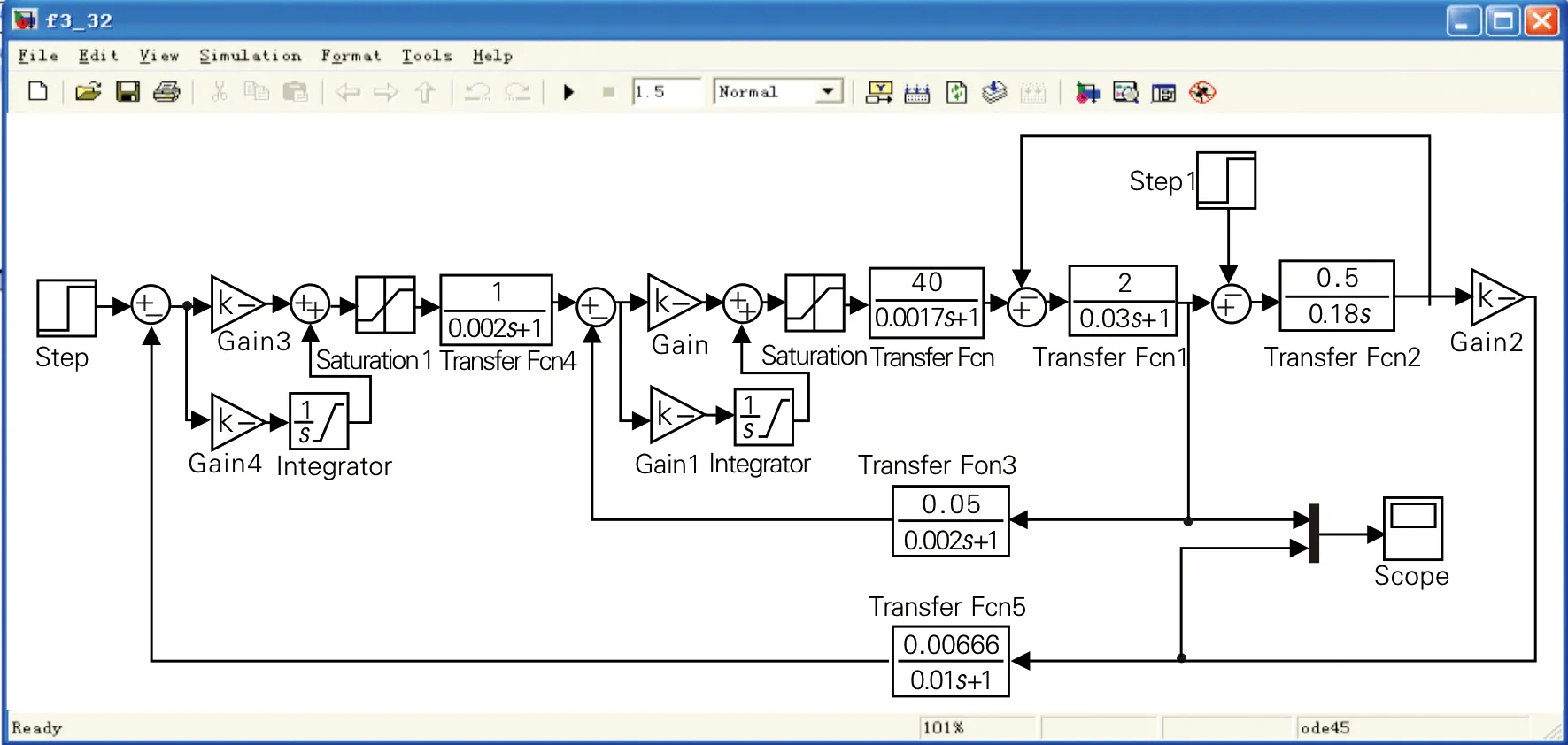
2.2 DTC系统建模与仿真

DTC系统是典型的交流调速系统，在DTC系统中应用面向控制系统结构图的方法进行建模仿真，电动机采用基于αβ坐标系的数学模型，转速环采用带限幅的PI调节器，在调节转速过程中，转矩和转速的上下波动可减小，提高了系统的稳定性[6]。定子磁链和转矩调节器采用带有滞环的双位式控制器，定子两相磁链分别为：

(1)

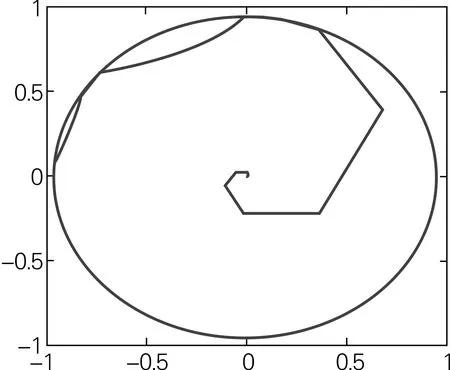
式(1)中：σ为电机的漏磁系数；再经过直角坐标到极坐标变换(K/P变换)得到定子磁链的幅值和角度；电压矢量环节选用SimuLink中的s函数编写[7]，其优点是控制思路明确，结构简洁，DTC系统仿真模型如图8所示，仿真中用ode23db变步长求解，步长为0.000 02 s。启动仿真得到仿真曲线，仿真中可根据仿真结果调整参数，直到与理论结果一致为止。定子磁链的轨迹图如图9所示，从图9中可见，系统启动时，磁链的幅值增长迅速，很快达到了磁链给定值，当系统负载变化时，磁链波形基本不变，反应在图中就是一个圆。定子三相电流、转矩和转速的波形如图10所示，从图10中可看到，三相电流波形按照三相正弦波的规律变化，启动电流比较大，但随着电机转速的提高，电流的幅值逐渐减小，并随着转速一起达到稳定状态。

由仿真结果来看，采用本控制策略进行直接转矩仿真，所得到的系统动静态特性都很优良，与理论分析结果吻合。可见应用面向对象原理图的仿真方法同样可以很方便地进行仿真实验，并在仿真中可以很方便地调整参数，适合应用于交流调速系统的仿真实验[8]。

3 结束语

基于Matlab的电气传动控制系统课程教学，将Matlab/Simulink仿真应用于课程教学中，并通过典型实例说明了其应用过程。将Matlab/Simulink用于课程教学，使课堂教学变得生动、直观，改变了传统教学过程中学生的被动学习状态，提高了学生对该课程的学习兴趣。在教学过程中，有效地将理论教学、实验教学和课程设计融为一体，通过对仿真结果进行分析，加深了学生对理论知识的理解[9]，增强了师生互动，提高了学习效率，通过仿真实验的实施也使学生的理论分析能力，实践能力和创新能力得到了提高，为以后完成毕业设计和工程实践打下了良好的基础。通过在近4届学生的课程教学中应用和实施新教学模式，取得了良好的教学效果，体现了其优势，可推广到其他课程教学中。

[1] 洪乃刚.电力拖动自动控制系统课程建设的实践[J].安徽工业大学学报,2003,20(1):78-79.

[2] 许胜，夏华凤，曹健.基于MATLAB的交互式课堂教学模式研究[J].电气电子教学学报，2015，37(6)：11-13.

[3] 阮毅,陈伯时.电力拖动自动控制系统-运动控制系统[M].北京：机械工业出版社,2013:88-93.

[4] 王忠礼，段慧达，高玉峰.MATLAB应用技术-在电气工程与自动化专业中的应用[M].北京：清华大学出版社，2013：122-124.

[5] 周渊深.交直流调速系统与MATLAB仿真[M].北京：中国电力出版社,2012:108-119.

[6] 蔡斌军，刘国荣.基于模糊控制滤波补偿的直接转矩控制系统[J].电力电子技术，2008,42(10):72-74.

[7] 胡学芝.基于模糊观测器的异步电机DTC系统研究[J].电力电子技术，2010,44(9):63-65.

[8] 许胜，夏华凤，曹健.基于Matlab 的交互式课堂教学模式研究[J].电气与电子教学学报，2015，37(6)：11-13.

[9] 李正，杨文换.《电机与拖动基础》虚拟实验的教学研究[J].中国电力教育，2008(21)：147-148.

(责任编辑 高 嵩)

Study on Course Teaching of Electrical Drive and Control System Based on Matlab

HuXuezhi

(School of Electrical and Electronic Information Engineering,Hubei Polytechnic University,Huangshi Hubei 435003)

Matlab has been used widely in engineering system simulation because of its powerful function of mathematical calculation and such advantages as modularization,structural programming and visualization of the Simulink simulation tool.Taking double closed loop DC speed control system and DTC system in AC speed regulation system respectively as an example,the application of Matlab/Simulink simulation in the teaching of electrical drive control system course is discussed and a teaching model of combination of theoretical teaching and simulation experiment is proposed.Through the implementation of the teaching model,good teaching effect has been obtained.

Matlab；simulation；teaching model；DTC；electrical drive and control system

2017-02-12

湖北理工学院校级教学研究项目(项目编号：2014B05)。

胡学芝，教授，硕士，研究方向：自动控制。

10.3969/j.issn.2095-4565.2017.02.014

G642.0

A

2095-4565(2017)02-0063-05