微型多分支钻管挠曲线典型力学模型研究

2017-05-02马向东任子汉

中国石油大学胜利学院学报 2017年1期

李雷,马向东,谌湛，任子汉

(1.中国石油大学胜利学院油气工程学院,山东东营 257061; 2.中国石化胜利石油工程公司井下作业公司培训中心,山东东营 257100; 3.东营金丰正阳科技发展有限公司,山东东营 257100; 4.中国石油大学(北京) 地球科学学院，北京 102249)

微型多分支钻管挠曲线典型力学模型研究

李雷1,马向东2,谌湛3，任子汉4

针对微型多分支钻管穿出轨道的过程,以弹塑性大挠度理论为基础,建立钻管穿出轨道的典型力学模型,推导得到钻管挠曲线的数学表达式,采用MATLAB进行计算,并通过室内试验进行验证。结果表明,力学模型计算值与室内试验值的相对误差均小于8%,在工程误差范围内且规律一致,验证了力学模型的可信度。

微型多分支;大挠度;力学模型;挠曲线

利用低成本高效益的增产技术来解决目前油藏开采面临的高成本低效益现状是非常必要的[1]。微型多分支增产技术既可对老油井进行改造,又可对新油井进行完井作业[2-3]。目前微型多分支作业工具已逐步完善,但仍缺乏钻管穿出轨道的机理解释,因此提供钻管穿出轨道的理论依据同样具有重要意义,可加快该技术的推广应用[4-5]。

1 力学模型建立

按照微型多分支增产技术工艺要求,作业前首先根据目标层的数量确定所需工具短节的个数,在地面组装完成后下入井内[6-9]。每个工具短节内预置4根高强度钻管和配套轨道,钻管材质为304不锈钢,每根钻管长10 m,钻管末端装有旋转射流喷嘴,作业流体采用磨料浆体。微型多分支工具下至预定位置后,开泵增压,多根钻管在内外压差作用下同步伸入地层,如图1所示。同时磨料浆体通过旋转射流喷嘴形成射流,破碎岩石形成孔道,为后续钻管的运动提供空间,典型的喷射压力为20 MPa。

按时间顺序分析微型多分支钻管穿出轨道的整个过程,初始阶段即钻管进入轨道未伸入地层阶段,钻管前端与轨道发生接触,与悬臂梁受端部集中力作用发生弹塑性变形的过程类似;中间阶段即钻管穿出轨道伸入地层较短距离阶段,位于轨道内的钻管局部与轨道发生接触,钻管前端与地层发生接触,前者占主导地位;最终阶段即钻管穿出轨道伸入地层较长距离阶段,位于轨道内的钻管局部与轨道发生接触,钻管穿出部分与地层发生接触,后者占主导地位。

图1 工具作业示意图

1.1 模型假设

微型多分支钻管穿出轨道的典型力学模型假设:(1)钻管为等截面实心圆轴;(2)忽略钻管重力;(3)钻管的变形仅为弯曲变形,忽略拉压变形;(4)由于钻管前端为喷嘴,强度较高,因此忽略钻管前端的变形;(5)钻管材料具有线弹性强化性质。根据钻管的受力特点建立钻管的典型力学模型,如图2所示。

1.2 模型分析

钻管端部受轴向拉力F1和集中力F2,轴向拉力F1大小不变,作用点始终位于钻管端部,方向始终与钻管端部切线平行,集中力F2作用点相对于钻管长度的位置、作用力大小和方向不变。初始阶段钻管与轨道内壁发生接触,钻管按照弹塑性变形分为L1塑性段和L2弹性段,当钻管向下运动穿出轨道较短距离时,假设L3为钻管向下运动量,L4为上阶段钻管塑性变形累积段,L5为弹性累积段。当钻管不断向下运动穿出轨道较长距离时,塑性累计段L4段长度不断增大,弹性段L5长度不断减小。在钻管穿过轨道初始阶段,集中力F2相对于轴向拉力F1占主导地位。当塑性累计段增加到整个长度,则在此基础上增加集中力F3,其方向与F2相反,此状态相当于钻管穿过轨道伸入地层较短距离阶段。在钻管穿过轨道伸入地层较长距离阶段(如图3)时,轴向拉力F1相对于集中力F2占主导地位。

图2 钻管典型力学模型示意图

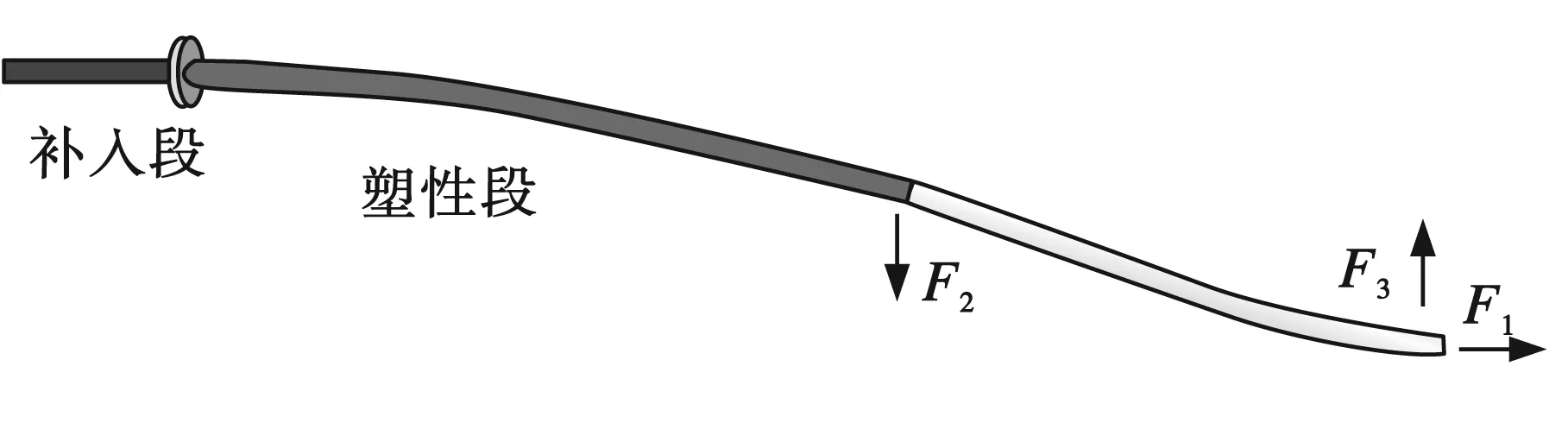
图3 钻管穿过轨道伸入地层较长距离阶段

当钻管进入轨道后,钻管与轨道发生接触干涉,钻管弯曲变形穿过轨道,各点的弯曲变形可直接叠加计算,记为原弯曲变形状态。当钻管穿出轨道后,由于弹性恢复导致钻管弯曲度减小,因此在原弯曲变形状态上须减去弹性卸载。当钻管与地层发生接触干涉时,钻管局部应力再次升高,相应的弯曲度再次发生改变,继而在原弯曲变形状态上叠加穿出轨道后再次积累的塑性弯曲变形进行计算。

2 模型推导

针对建立的微型多分支钻管典型力学模型,借鉴一端固定,一端自由的Euler压杆力学模型和在自由端承受方向向下集中力的水平悬臂梁力学模型,利用类似的弹塑性弯曲数学处理方法来推导钻管的典型挠曲线方程[10-11]。

钻管在弹塑性弯曲状态下的无量纲弯矩m和无量纲曲率φ关系为

(1)

钻管发生弯曲的Elastica方程组见式(2),Plastica方程组见式(3)。

(2)

(3)

式中,θ为钻管轴线与x轴的夹角;μ为钻管材料的强化系数;s为该点到原点的钻管长度;β=MeL/EI,L为横截面为圆形的钻管长度;Me为横截面为圆形的钻管的最大弹性弯矩;EI为横截面为圆形的钻管的抗弯刚度。

分析可知,BC段内任一点的弯矩可表示为

m=1+f(xp-x) .

(4)

当钻管固定端B处的最大弯矩超过钻管截面的最大弹性弯矩Me时,塑性区将从钻管固定端B处向自由端A处扩展。在集中力F作用下的钻管形状和各参数表示如图4所示,其中BC段为塑性区,CA段为弹性区,C点为弹塑性区分界点,且在C点M=Me,m=1。悬臂梁在端部横向集中力作用下的弹塑性大变形如图4所示。

图4 悬臂梁在端部横向集中力作用下的弹塑性大变形

推导得到塑性BC段挠曲线的x,y表达式见式(5),弹性CA段挠曲线的x,y表达式见式(6)。

(5)

(6)

从钻管初始水平状态开始计算,从固定端以恒定长度加入补入钻管段,F2作用点距离固定端的长度是定值,钻管超出此长度后继续按照累加、卸载规律进行计算,按照上述推导得到的挠曲线公式,通过MATLAB计算可得到钻管轴线各点坐标,进而描述钻管挠曲线(图5)。

图5 钻管挠曲线的室内试验与计算对比

3 室内试验

对不同材质钻管进行室内试验,试验轨道为圆弧型,出口角度40°,钻管尺寸为12 mm×1 mm。由于油缸和实验台长度限制,实验中钻管推进距离为1.5 m。试验装置简化示意图见图6,对比力学模型的计算结果见图5。

图6 钻管穿出轨道送进试验示意图

分析可知,不同钻管伸出长度时,钻管挠曲线室内试验测量值与力学模型计算值的相对误差均小于8%,在工程误差范围内且规律一致,验证了钻管穿出轨道力学模型的可信度。

4 结束语

基于弹塑性大挠度理论建立了微型多分支钻管穿出轨道的力学模型,可定量描述钻管的变形形态,通过试验证实其计算结果的可信度。本文的推导及试验未考虑地层的情况,后续可将其考虑在内进行数值模拟软件计算或开展全尺寸工具试验研究。

[1] 邹才能.常规-非常规油气“有序聚集”理论认识及实践意义[J].石油勘探与开发,2014,41(1):14-26.

[2] FREYER R. Multilateral system allowing 100 level 5 laterals drilled simultaneously[R]. SPE 121814,2011.

[3] RICE K, JORGENSEN T.First installation of efficient and accurate multilaterals stimulation technology in carbonate oil application[R]. SPE 171021,2014.

[4] RICE K, JORGENSEN T. Technology qualification and installation plan of efficient and accurate multilaterals drilling stimulation technology for sandstone oil application[R]. SPE 174035,2015.

[5] FREYER R. Method and device for making lateral openings out of a wellbore: 8322409B2 [P]. 2012.

[6] FREYER R. Method and a device for solvent injection in a subsurface well: 0223669A1 [P]. 2009.

[7] FREYER R. Method and jetting head for making a long and narrow penetration in the ground: 0273276A1 [P]. 2012.

[8] FREYER R. Method and device for connecting a pipe to a confi- nement of a subsurface borehole: 0124221A1 [P]. 2014.

[9] PRISKILA L M. Evaluation of fishbone lateral stimulation[D].Nor- way: Norwegian University of Science and Technology,2014.

[10] 余同希.塑性弯曲理论及其应用[M].北京:科学出版社,1992:87-124.

[11] 伍小强.悬臂梁弹塑性大挠度全过程的分析[J].力学学报,1986,18(6):516-527.

[责任编辑] 时凤霞

2017-01-20

李雷(1990—)，男，黑龙江大庆人，中国石油大学胜利学院油气工程学院助教，硕士，主要从事钻井工具研究。

10.3969/j.issn.1673-5935.2017.01.007

TE19