基于二维插值模型的等照度曲线的绘制

韩 臻，张九红

(沈阳建筑大学建筑与规划学院，辽宁 沈阳 110168)

基于二维插值模型的等照度曲线的绘制

韩 臻，张九红

(沈阳建筑大学建筑与规划学院，辽宁 沈阳 110168)

本文从等照度曲线的基本概念出发，建立二维插值模型，采用双线性插值法与三次内插值算法绘制等照度曲线。再通过工程实例，利用MATLAB编程定量比较传统的平均值法绘制的等照度曲线与新的算法绘制的等照度曲线在精确度上的差异。

等照度曲线；二维插值；MATLAB

引言

照明设计旨在为使用者提供一个良好的光环境，以使其得以正常的学习、工作、生活[1]。使用者可以在良好的光环境下正常地发挥自身的视觉、听觉、智力等因素以完成自身活动。而在学校、工厂等对工作面照度要求较高的场所，过高或过低的照度值不仅会使人工作效率下降，更会损害人的身体健康。因此在确定了灯具种类、照明方式及灯具布置方法之后根据工作面上的等照度曲线对室内照明设施进行检验是十分必要的。传统的等照度曲线一般采用平均值法，这种算法所需数据量大，照度测量过程繁琐且所绘等照度曲线精确度低，误差大。在一些对精确度要求较高的场所，传统的等照度曲线无法准确的描述工作面上照度分布情况，从而会对照明设计产生一定的影响。本文建立的二维插值模型所采用的双线性插值算法和三次内插值算法可绘制更加精准的等照度曲线，并且所需测点数较少，方便设计师进行测量、计算。

1 等照度曲线的概念及作用

等照度曲线是指将指定工作面上照度值相同的所有点用适当坐标系(平直角坐标系或极坐标系)绘成的曲线，如图1所示。

图1 直角坐标系等照度曲线Fig.1 Iso-illuminance curve in rectangular coordinate system

测量点的选取应采用中心点照度测量法或四点照度测量法。工作面上选择的测量点的照度值可根据测点至点光源的距离r以及点光源在i方向上的发光强度I计算得出。

(1)

式中E为测点的照度值；I为点光源在i方向上的发光强度；r为测点至点光源的距离。

等照度曲线在建筑设计及工程检验中有着极其重要的作用。一是检验室内照明设施是否满足《建筑照明设计标准》(GB 50034—2013)的要求；二是检验室内照明设施是否满足室内的设计条件。

2 二维插值模型的建立

通过已知的有限个数据点的近似函数进行取值的过程称为插值。若已知节点为一维变量，则插值函数为一元函数，此时称为一维插值；若已知数据构成网格，即节点为二维节点时，则插值函数为二维函数(曲面)，此时则称为二维插值。二维插值常用的方法有双线性插值法、三次内插值法、Nearest法等。本文分别采用双线性插值法和三次内插值法绘制等照度曲线。

2.1 双线性插值法

双线性插值法是二维插值模型中较为常用的算法之一，双线性插值法是根据点O(x0,y0)周围相邻的四个点的照度值，通过两次插值计算得出其照度值f(x0,y0)，如图2所示。

图2 双线性插值原理示意图Fig.2 Schematic diagram of bilinear interpolation principle

首先计算α和β。

(2)

根据f(m,n)和f(m,n+1)插值求f(m,y)。

f(m,y)=f(m,n)+
α[f(m,n)-f(m,n+1)]

(3)

再根据f(m+1,n)和f(m+1,n+1)插值求f(m+1,y)。

f(m+1,y)=f(m+1,n)+
α[f(m+1,n)-f(m+1,n+1)]

(4)

最后根据f(m,y)和f(m+1,y)二次插值求f(x,y)。

f(x,y)=f(m,y)+
β[f(m+1,y)-f(m,y)]

(5)

将式(3)与式(4)代入式(5)，整理得到

f(x,y)=f(m,y)+β[f(m+1,n)-
f(m,n)]+αβ[f(m+1,n)+f(m,n+1)-f(m,n)-f(m+1,n+1)]

(6)

故工作面上任意一点的照度值可由其周围四个测点的照度值根据式(6)进行二维插值得到。

2.2 三次内插值法

为了更加精确的计算点O(x0,y0)的照度值，取得更加良好的插值效果。本文在此建立三次内插值算法的模型绘制等照度曲线，以比较双线性插值法与三次内插值法的不同。

若用插值函数s(x)=sin(πx)/(πx)对测点的照度值进行插值，这时不仅需要考虑直接相邻的四个测点对计算点O的影响，还应该考虑周围的16个测点的照度值对其的影响，如图3所示。

插值函数s(x)可采用式(7)近似。

(7)

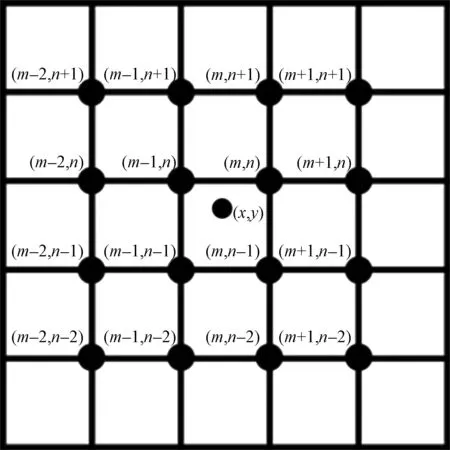
图3 三次内插值原理示意图Fig.3 Schematic diagram of the three interpolation principle

三次内插值法计算点O照度值的方法与双线性插值法近似，首先计算s(2+α)，s(1+α)，s(α)，s(1-α)以及s(2+α)，s(1+α)，s(α)，s(1-α)；再根据f(m-2,n)，f(m-1,n)，f(m,n)，f(m+,n)计算f(x0,n)，同理可求f(x0,n-2)，f(x0,n-1)和f(x0,n+1)。最后根据f(x0,n-1)，f(x0,n)，f(x0,n+1)，f(x0,n+2)求出f(x0,y0)。

上述计算过程可用矩阵表示，如式(8)～式(10)所示。则工作面上所计算的点的照度值f(x0,y0)为

f(x0,y0)=XYZ

(11)

3 工程实例

以沈阳某高校图书馆地下室走廊为例，利用

X=[s(2+α)s(1+α)s(α)s(1-α)]

(8)

(9)

Z=[s(2+β)s(1+β)s(β)s(1-β)]T

(10)

MATLAB软件[2]分别用双线性插值和三次内插值两种算法进行插值计算，绘制工作面的等照度曲线，并与传统测量方法进行对比。测点布置图如图4所示，图中M、N、O、P、Q和R六个点为检验点，用以比较不同算法绘制的等照度曲线值与真实值的相对误差的大小。

图4 测点布置图Fig.4 Layout of measuring points

根据国家规范，走廊、流动区域的工作面为地面，使用XYC-I全数字色度计测量工作面上各测点的照度值并记录如表1所示。

表1 测点照度记录表Table 1 Illuminance of measuring point lx

将数据代入MATLAB程序中进行计算机运算，分别画出双线性插值和三次内插值所得到的等照度曲线，分别如图5、图6所示。

图5 双线性插值法等照度曲线Fig.5 Iso-illuminance curve painted by bilinear interpolation algorithm

图6 三次内插值法等照度曲线Fig.6 Iso-illuminance curve painted by three interpolation algorithm

为了检验各个模型所绘制的等照度模型的精确度，现将六个检验点的实测值以及各种算法算得出的照度值记录如表2所示。

表2 检验点照度值记录表Table 2 Illuminance of test points lx

根据《建筑照明设计标准》(GB 50034—2013)[3]，走廊、流动区域的工作面最低照度值为50 lx。由等照度曲线可知：此走廊只有中间部分满足照明规范，因此应重新选择灯具或改变灯具的布置间距以提高工作面的照度值以满足国家规范的要求。

4 结论

传统的平均值法绘制的等照度曲线与双线性插值算法绘制的等照度曲线都属于线性插值，平均值法仅仅取四个测点的照度值的平均数作为其中心点的照度值，而双线性插值法可根据周围四个测点的照度值对区域内任意一点进行插值，传统的平均值法要想到达同样的精度只能细分网格，增大测点数量。

同时，由图5与图6直观上可以看出双线性插值法绘制的等照度曲线远不如三次内插值法绘制的等照度曲线光滑，由于其采用线性插值的方法，使得其曲线在转折处较为生硬。而三次内插值算法其插值函数s(x)=sin(πx)/(πx)对计算点进行三次插值，使得其曲线更加光滑，精确度也高于双线性插值算法所绘制的曲线。

通过实测值与计算值的对比，由图8可以直观的看出三次内插值算法绘制的等照度曲线的相对误差要远低于双线性插值的。计算可得其精确度比双线性插值算法提高了40%。若想达到相同的精确度，双线性插值算法所绘制的等照度曲线也只能利用微分的思想：细分网格、增加测点个数，不停地逼近三次曲线，这就大大增加了等照度曲线绘制的时间与计算量。同时，由于其采用线性插值函数，即使其测点数增加，其曲线转折处依旧没有三次内插值算法所绘制的等照度曲线光滑。

图7 各算法照度计算值示意图Fig.7 Measured value of illumination

图8 各算法照度计算相对误差示意图Fig.8 Relative error of illuminance

目前建筑设计越来越重视室内的建筑物理环境设计，等照度曲线在室内照明设施检验中也起到了越来越重要的作用。为此，需要设计师能够更加准确的绘制等照度曲线，做出理想的建筑室内照明设计。

[1] 柳孝图.建筑物理[M].第3版.北京:中国建筑工业出版社,2010.

[2] 赵小川.MATLAB图像处理——程序实现与模块化仿真[M].北京:北京航空航天大学出版社,2014.

[3] 建筑照明设计标准:GB 50034—2013[S].北京:中国建筑工业出版社,2013.

To Draw the Iso-illuminance Curve Using Two-dimensional Interpolation Method

HAN Zhen, ZHANG Jiuhong

(SchoolofArchitectureandUrbanPlanning,ShenyangJianzhuUniversity,Shenyang110168,China)

In this paper, based on the basic concept of the iso-illuminance, a two-dimensional interpolation model is established, and the bilinear interpolation algorithm and the three interpolation algorithm are used to draw the curve. Through the engineering example, the paper uses MATLAB to compare the difference of the iso-illuminance curve drawn by the traditional method and the new algorithm.

iso-illuminance curve; two-dimensional interpolation; MATLAB

张九红：E-mail: 364798540@qq.com 基金项目：国家自然科学基金(基于知觉适应的寒地建筑室内外过渡空间热—光交互作用机理与评价体系研究)

TM923

A

10.3969/j.issn.1004-440X.2017.02.011