圆锥规划问题的光滑牛顿方法

迟晓妮, 汪洋, 刘博

(1.桂林电子科技大学数学与计算科学学院/广西密码学与信息安全重点实验室,广西 桂林 541004; 2.桂林电子科技大学数学与计算科学学院/广西自动检测技术与仪器重点实验室,广西 桂林 541004; 3.桂林电子科技大学数学与计算科学学院/广西高校数据分析与计算重点实验室,广西 桂林 541004)

圆锥规划问题的光滑牛顿方法

迟晓妮1, 汪洋2, 刘博3

(1.桂林电子科技大学数学与计算科学学院/广西密码学与信息安全重点实验室,广西 桂林 541004; 2.桂林电子科技大学数学与计算科学学院/广西自动检测技术与仪器重点实验室,广西 桂林 541004; 3.桂林电子科技大学数学与计算科学学院/广西高校数据分析与计算重点实验室,广西 桂林 541004)

给出求解圆锥规划问题的一种新光滑牛顿方法.基于圆锥互补函数的一个新光滑函数,将圆锥规划问题转化成一个非线性方程组,然后用光滑牛顿方法求解该方程组.该算法可从任意初始点开始,且不要求中间迭代点是内点.运用欧几里得代数理论,证明算法具有全局收敛性和局部超线性收敛速度.数值算例表明算法的有效性.

圆锥规划;光滑牛顿方法;光滑函数;局部超线性收敛

1 引言

对任意x,y∈Rn,(x,y)表示(xT,yT)T,x=(x0,x1)∈R×Rn−1表示‖.‖表示欧氏范数,I是(n−1)阶单位矩阵.n-维圆锥的定义[1]为

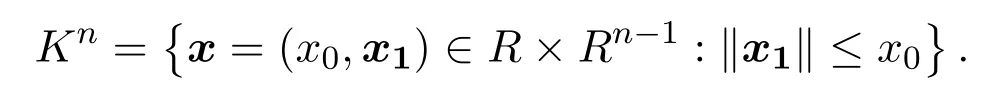
由文献[2]知圆锥与二阶锥之间的代数关系:对任意x,s∈Rn,

有[3]

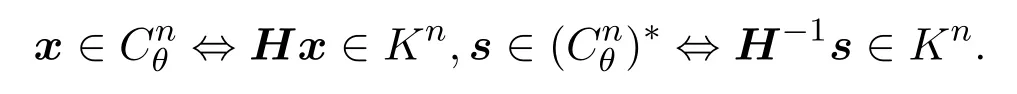
其中

且H−1是H的逆矩阵.这里对偶锥,即

考虑圆锥规划问题(CCP)[4]

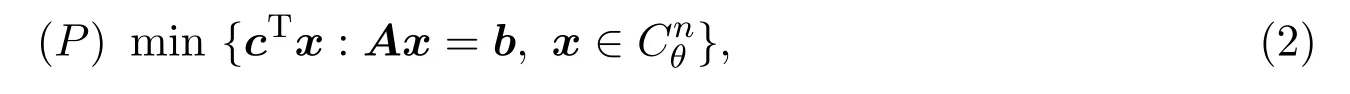
其中A∈Rm×n,c∈Rn和b∈Rm.

CCP(2)的对偶问题[4]是

其中y∈Rm.

CCP是一类非光滑非对称锥凸优化问题,有非常重要而又广泛的应用背景,其研究问题涉及金融、控制、图像处理和工程[5-7]等领域.如多指机器人最优抓取操作和四足机器人动力分配优化等问题.所以CCP的算法研究具有重要的理论意义和实际应用价值.近年来,圆锥优化问题备受关注,但由于圆锥是非对称锥,给研究带来了很多困难.2013年,Zhou和Chen[2]研究了圆锥的性质和与圆锥相伴的谱分解.基于圆锥与二阶锥的代数关系,Bai,Gao和Wang[3]给出求解凸二次圆锥规划的内点法.目前关于CCP的算法尚不多见.

本文基于文献[8]的一个圆锥互补函数,给出一个圆锥互补函数[8]的光滑函数,并提出求解CCP的一个光滑牛顿方法.该算法对初始点没有限制,且不要求中间迭代点是内点.在每次迭代中,只需求解一个线性方程组和进行一次线搜索.运用欧几里得约当代数理论,证明算法是全局收敛并且是局部超线性收敛的.数值算例表明算法的有效性.，

2 预备知识

本节介绍与二阶锥相伴的欧几里得约当代数[9].对任意 x=(x0,x1)∈R×Rn−1和s=(s0,s1)∈R×Rn−1,定义约当积为:

其单位元e=(1,0,...,0)∈Rn.对任意x=(x0,x1)∈R×Rn−1,定义箭形矩阵为:

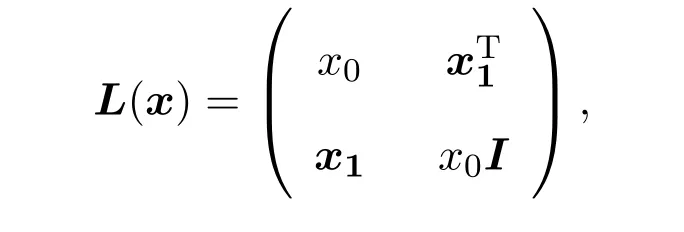
易知对任意 x,s∈Rn有 L(x)s=x◦s.下给出二阶锥中的向量谱分解[9].对任意 x= (x0,x1)∈R×Rn−1,其谱分解为

其中特征值

u(1)和u(2)是分别属于特征值λ1和λ2的特征向量

如果 x10,则否则ω∈Rn−1是满足‖ω‖=1的任意向量.

本文假设CCP(2)和(3)严格可行,即F0(P)×F0(D)∅.CCP(2)和(3)的严格可行解集分别为:

而

故由强对偶理论[4]可知,CCP(2)和(3)都存在最优解且其最优值相等.此外,若(x∗,y∗,s∗)是CCP(2)和(3)的最优解当且仅当(x∗,y∗,s∗)满足如下最优性条件:

3 光滑牛顿方法

本节基于圆锥互补问题的一个光滑函数,给出求解CCP(2)和(3)的一个新光滑牛顿方法.由文献[7]知函数

将(6)式进行光滑化得到

其中µ∈R.

定理 3.1对任意的一个光滑函数.

证明类似定理2.4[10]的证明,略去.

令z:=(µ,x,y,s)∈R++×Rn×Rm×Rn,定义函数

本节基于圆锥互补函数的光滑函数(8),将CCP(2)和(3)的最优性条件(5)转化成一个非线性方程组Φ(z)=0.当µ＞0时,在每步迭代中应用光滑牛顿方法求解方程组Φ(z)=0.令 µ↓0时,可得 CCP最优性条件 (5)的解.记 z∗:=(µ∗,x∗,y∗,s∗),当 µ∗=0时,显然Φ(z∗)=0⇔(x∗,y∗,s∗)是CCP(2)和(3)的解.

定理 3.2设A行满秩,且Φ(z)由(9)式定义,则下列结论成立.

(i)Φ(z)是全局Lipshitz连续且强半光滑,且在任意z=(µ,x,y,s)∈R++×Rn×Rm×Rn处连续可微,其雅可比矩阵为

其中

(ii)对任意z=(µ,x,y,s)∈R++×Rn×Rm×Rn,Φ′(z)可逆.

证明由定理2.3[3]的证明,易知(i)成立.

(ii)令Δz:=(Δµ,Δx,Δy,Δs)∈R×Rn×Rm×Rn是Φ′(z)零空间中任一向量,只需证Δz=0.由(10)式知,

由(11)式和(13)式得

在(14)式的左右两边同时左乘L(w),有

由D(µ,x,s)和E(µ,x,s)的定义及H是对角阵有

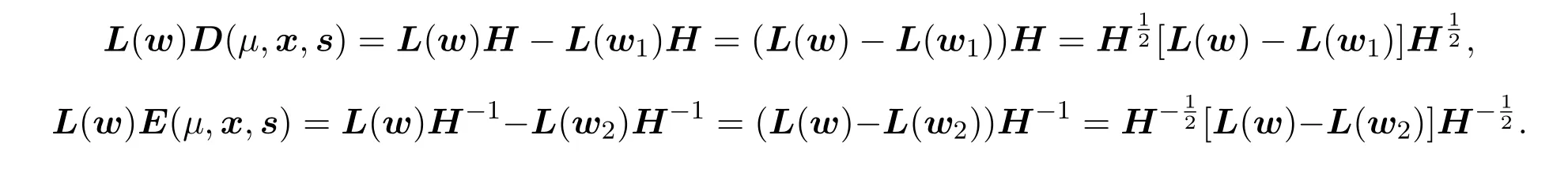
又因为

由引理3.1[11]得到L(w)D(µ,x,s)和L(w)E(µ,x,s)都是正定矩阵必可逆,且

的对称部分正定.在(15)式两边同时左乘△xT[L(w)E(µ,x,s)]−1有

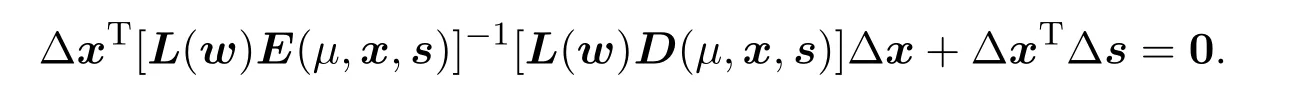
又由(11)式和(12)式得ΔxTΔs=−ΔxTATΔy=−(AΔx)TΔy=0,从而有

又[L(w)D(µ,x,s)][L(w)E(µ,x,s)]的对称部分正定,从而

定义函数Ψ:R+×Rn×Rm×Rn→R+为

算法3.1(求解CCP的光滑牛顿方法)

步2 解线性方程组

求得搜索方向Δzk:=(Δµk,Δxk,Δyk,Δsk)∈R×Rn×Rm×Rn.

步3 令lk是满足下列不等式的最小非负整数l

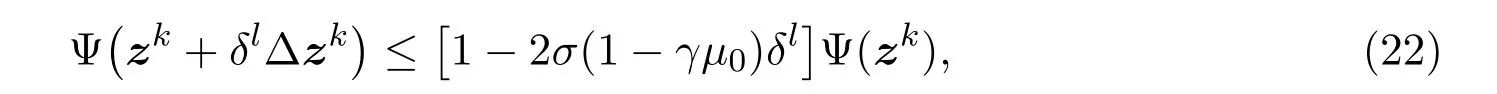
确定步长λk=δlk.

步4 令zk+1:=zk+λkΔzk,k:=k+1.转步1.

定义集合

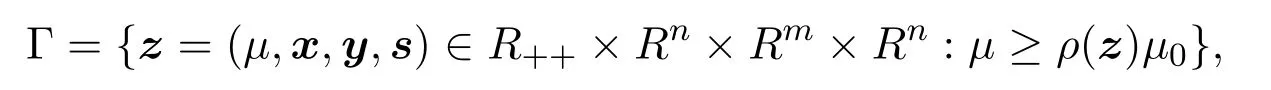
其中ρ(z)由(20)式定义.

定理 3.3设A行满秩,且{zk=(µk,xk,yk,sk)}是算法3.1生成的序列,则算法3.1是适定的.

证明当µ＞0由定理 3.2知Φ′(z)可逆,故步2是适定的.由引理5[13]的证明能得出步3适定.证毕.

引理 3.1设{zk=(µk,xk,yk,sk)}是算法3.1产生的迭代序列,则对任意k≥0有以下结论成立.

(i){ρ(zk)}是一个单调递减序列;

(ii)对任意k≥0有 µk＞0和zk∈Γ.

证明 (i)由(20)式知{ρ(zk)}是一个单调递减序列.

(ii)用数学归纳法证明.假设µk＞0.由定理3.3知对任意

Φ′(z)可逆.由(21)式得

由引理 4.2[13]知对于任意µ＞0有e−µ−1≥−µ,从而

又由µ0＞0和λk∈(0,1)可得对任意k≥0有µk≥0.

由ρ(zk)的定义(20)得ρ(z0)≤γ＜1,即µ0≥µ0ρ(z0),所以z0∈Γ.假设µk≥ρ(zk)µ0.

则由(30)式和(i)得

故对任意k≥0有zk∈Γ.

4 收敛性分析

下面分析算法3.1的全局收敛性和局部超线性收敛速度.

定理 4.1设A行满秩且{zk=(µk,xk,yk,sk)}是算法3.1生成的序列,则{zk}的任一聚点z∗:=(µ∗,x∗,y∗,s∗)都是Φ(z)=0的解,从而(x∗,y∗,s∗)是CCP(2)和(3)的解.

证明不失一般性,设由(22)知Ψ(zk)单调递减有下界,故

若 Ψ(z∗)=0,则结论成立.反证法,设 Ψ(z∗)＞ 0,由 zk∈Γ和 ρ(zk)的定义知 µ∗≥γµ0min{1,Ψ(z∗)}＞0.由定理 3.2知 Φ′(z∗)存在且可逆,故存在 z∗的一个闭邻域 N(z∗),使得对任意 z∈N(z∗)有 µ∈R++,所以 Φ′(z)可逆.对任意 z∈N(z∗),令 Δz= (Δµ,Δx,Δy,Δs)是方程组Φ(z)+Φ′(z)Δz=eµρ(z)的唯一解.故由引理5[13]的证明知存在一个常数∈(0,1),使得对任意有

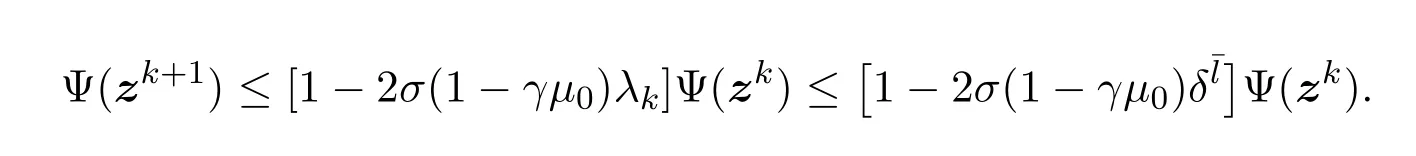
定理 4.2(局部超线性收敛)若A行满秩,z∗是算法3.1产生的序列{zk}的任意聚点,且任意V ∈∂Φ(z∗)非奇异,则{zk}收敛到{z∗},即

证明由定理4.1知z∗是Ψ(z)=0的一个解，由于V ∈∂Φ(z∗)非奇异.由命题3.1[14]当zk充分接近z∗有

由定理3.2知Φ(·)全局Lipshitz连续且在z∗点强半光滑,则对于zk充分接近z∗有

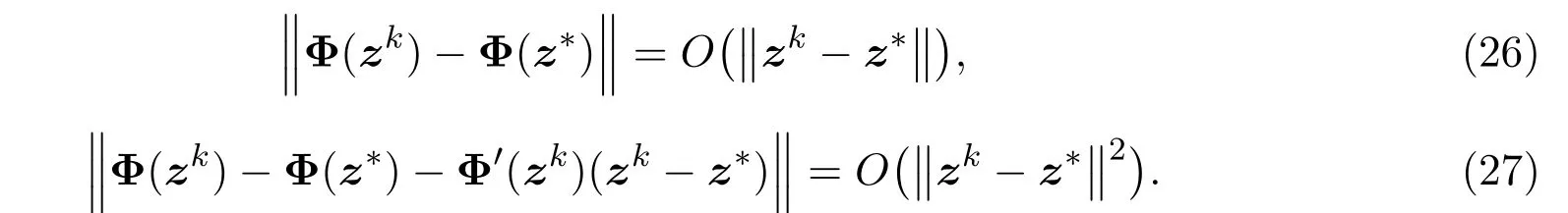
由(21),(25),(26)和(27)式,得

由定理4.1[15]的证明知,当zk充分接近z∗时有

由定理3.2知Φ(·)全局Lipshitz连续,故由(28)式和(29)式知当zk充分接近z∗时得

因而由算法3.1的步3知,当zk充分接近z∗时有

由 (28)和(30)式得

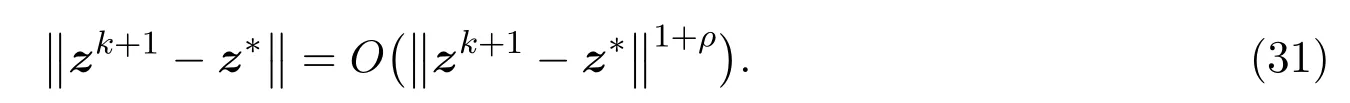
又由定理4.1和(20)式得,当zk充分接近z∗时

由(21),(29)和(31)式知当k充分大时有

因为对于任意µ＞0,e−µ−1≤−µe−µ,两边同乘以−eµ变为µ≤eµ−1,故

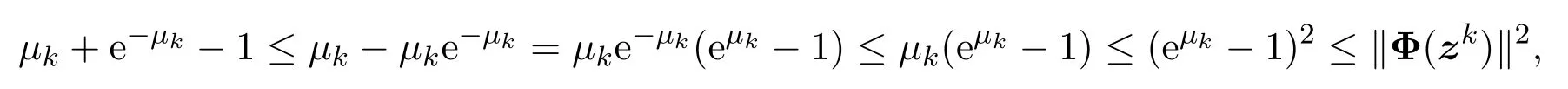
所以

故由(26),(29),(31)和(33)式得

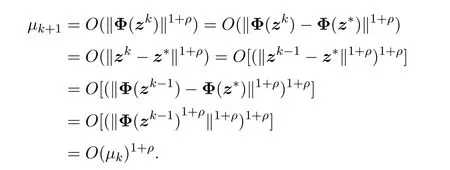
证毕.

5 数值算例

运用Matlab(R2012a)编程,在Intel(R)Xeon(R)CPU E3-1226 v3@3.30GHz 4GB内存, Windows 10操作系统的计算机上做数值算例,测试算法3.1的数值效果.试验测试问题是随机生成规模m(n=2m)从100到500的CCP.对每种规模问题产生10个问题进行求解.

运用算法3.1求解随机生成的CCP.算法3.1当ρ=1时为局部二次收敛其余参数取值为µ0=0.01,δ=0.75,σ=0.45,γ=0.65.当‖Φ(z)‖≤10−8算法3.1停止.Iter指平均迭代次数,ACPU指平均CPU时间.

首先随机生成一个行满秩的矩阵A∈Rm×n和向量x∈int Cnθ,s∈int(Cnθ)∗,y∈Rm.令b=Ax和c=ATy+s.由于CCP(2)和(3)严格可行,故CCP(2)和(3)存在最优解且其最优值相等.然后分别选旋转角表5.1中以x0=e∈Rn,y0=0∈Rm为初始点,给出用算法3.1求解不同旋转角的和不同规模的CCP的Iter和ACPU.数值结果表明算法3.1在求解不同规模的CCP时,随着问题规模变大所需CPU时间会增加,迭代次数受问题规模和旋转角的影响较小.

对每一个给定的θ值,均随机生成10个问题并运用不同的初始点进行求解.当时,CCP即为二阶锥规划问题(SOCCP).表5.2给出运用算法3.1求解不同初始点和不同ρ取值的SOCCP所需的CPU时间和迭代次数.数值结果表明,不同初始点和不同ρ值对算法3.1求解CCP所需的CPU时间和迭代次数影响不大.表5.3给出运用算法3.1与Qi-Sun-Zhou算法[12]求解SOCCP的CPU时间和迭代次数.数值算例结果表明算法3.1通常比Qi-Sun-Zhou算法所需的迭代次数和CPU时间都少.

从表5.1-5.3的数值结果看出,运用算法3.1求解CCP所需的CPU时间和迭代次数较少,且相对稳定.从而表明算法3.1的有效性.

表5.1 运用算法3.1求解不同规模和旋转角的CCP的数值结果.

表5.2 运用算法3.1求解不同初始点和不同ρ取值的SOCCP的数值结果.

表5.3 算法3.1和Qi-Sun-Zhou算法的性能比较.

[1]Dattorro J.Convex Optimization and Euclidean Distance Geometry[M].California:Meboo Publishing, 2005.

[2]Zhou J C,Chen J S.Properties of circular cone and spectral factorization associated with circular cone[J]. Journal of Nonlinear and Convex Analysis,2013,14(4):1504-1509.

[3]Chi X N,Liu S Y.A one-step smoothing Newton method for second-order cone programming[J].Journal of Computational and Applied Mathematics,2009,223:114-123.

[4]Bai Y Q,Ma P F,Zhang J.A polynomial-time interior-point method for circular cone programming based on kernel functions[J].Journal of Industrial and Management Optimization,2016,12(2):739-756.

[5]Li Z J,Ge S Z,Sam,etal.Contact-force distribution optimization and control for quadruped robots using both gradient and adaptive neural networks[J].IEEE Transactions on Neural Networks,2014,25(8):1460-1473.

[6]Ko C H,Chen J S.Optimal grasping manipulation for multifingered robots using semismooth Newton method[J].Mathematical Problems in Engineering,2013,2013(3):206-226.

[7]Bomze I.Copositive optimization-Recent developments and applications[J].European Journal of Operational Research,2012,216(3):509-520.

[8]Miao X H,Guo S J,Qi N,etal.Constructions of complementarity functions and merit functions for circular cone complementarity problem[J].Computation Optimization Applications,2016,63:495-522.

[9]Alizadeh F,Goldfarb D.Second-order cone programming[J].Mathematical Programming,2003,95:3-51.

[10]Chi X N,Liu S Y.A non-interior continuation method for second-order cone programming[J].Optimization 2009,58(8):965-979.

[11]Fukushima M,Luo Z,Tseng P.Smoothing functions for second-order-cone complementarity problems[J]. SIAM Journal on Optimization,2002,12:436-460.

[12]Qi L Q,Sun D F,Zhou G L.A new look at smoothing Newton methods for nonlinear complementarity problems and box constrained variational inequalities[J].Mathematical Programming,2000,87:1-35.

[13]Jiang H.Smoothed Fischer-Burmeister equation methods for the complementarity problem[J].Department of Mathematics,1997,153:3-4.

[14]Qi L Q,Sun J.A nonsmooth version of Newton’s method[J].Mathematical Programming,1993,58(1):353-367.

[15]Qi L Q.Convergence analysis of some algorithms for solving nonsmooth equations[J].Mathematics of Operations Research,1993,18(1):227-244.

A smoothing Newton algorithm for circular cone programming

Chi Xiaoni1,Wang Yang2,Liu Bo3
(1.School of Mathematics and Computing Science,Guangxi Key Laboratory of Cryptography and Information Security,Guilin University of Electronic Technology,Guilin 541004,China; 2.School of Mathematics and Computing Science,Guangxi Key Laboratory of Automatic Detection Technology and Instrument,Guilin University of Electronic Technology,Guilin 541004,China; 3.School of Mathematics and Computing Science,Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation,Guilin University of Electronic Technology,Guilin 541004,China)

A new smoothing Newton method is presented for solving circular cone programming in this paper. Based on a new smoothing function of circular cone complementary function,the circular cone programming is reformulated as a nonlinear system of equations,and then a smoothing Newton method is given to solve this nonlinear system of equations.The proposed algorithm may start from any initial point,and the intermediate points don’t need to be interior points.We prove that the algorithm has the global convergence and local superlinear convergence by the Euclidean algebra theory.The numerical results illustrate the validity of the algorithm.

circular cone programming,smoothing Newton method,smoothing function, local superlinear convergence

O221

A

1008-5513(2017)02-0111-11

10.3969/j.issn.1008-5513.2017.02.001

2017-02-28.

国家自然科学基金(11401126,71461005,11661002);国家级大学生创新创业计划项目(201610595037);广西自然科学基金(2016GXNSFBA380102,2014GXNSFFA118001);广西密码学与信息安全重点实验室研究课题(GCIS201618);广西自动检测技术与仪器重点实验室基金(YQ15112,YQ16112).

迟晓妮(1979-),副教授,研究方向:最优化理论与算法.

2010 MSC:90C25