基于MATLAB GUI 功能的产业发展调控可视化

王万宾，李 森，张星梓，任 静，贾海峰，陈异晖

(云南省环境科学研究院环境规划研究中心，云南 昆明650034)

基于MATLAB GUI 功能的产业发展调控可视化

王万宾，李 森，张星梓，任 静，贾海峰，陈异晖

(云南省环境科学研究院环境规划研究中心，云南 昆明650034)

实现基于资源环境承载力约束条件下的产业发展调控可视化将为环境规划管理者提供有效决策依据。本研究首先在水资源量、土地资源量(耕地面积、建设用地面积)、污染物环境容量(COD、NH4-N、SO2、NOx)、粮食产量等约束条件下，分别建立了经济和人口最大化、资源环境利用参数(单位产值用水量、污染物排放量等)最优化为目标函数的规划模型，然后以MATLAB GUI功能为基础，实现了其可视化。最后，通过简单实例分析，验证了基于MATLAB GUI功能的产业发展调控可视化程序的适用性及正确性。

MATLAB；GUI；产业发展调控；资源环境承载力；可视化

当前，资源环境承载力分析及产业发展调控被广泛应用于环境规划中。作为环境规划系统重要的组成部分，基于资源环境承载力的产业发展调控研究已引起广大研究者的兴趣[1-5]。目前，对于部分资源环境承载力(比如水环境[6, 7])的产业发展调控的研究众多，但缺少综合及全面的基于资源环境承载力约束的产业调控研究。在大量的产业发展调控研究中，线性规划模型得到了普遍的应用。MATLAB GUI功能的可视化及其程序的易于封装，为实现产业发展调控可视化提供了坚实的基础[8, 9]。本研究将基于线性规划的基本理论及MATALB GUI 方法，以资源环境承载力(水资源、土地资源、污染物环境容量等)约束为前提，实现产业发展调控的两个子功能：规划未来的资源环境利用效率，获知最佳发展人口和经济规模；规划未来的产业发展趋势，获知最优的资源环境利用效率。基于资源环境承载力约束的产业发展调控规划模型的完善，将进一步指导规划模型在产业发展调控中的应用研究。基于MATLAB GUI功能的产业发展调控的可视化，将为政府管理部门做出决策提供理论依据和科学支撑。

1 材料与方法

1.1 规划模型方法

线性规划问题是在一组线性约束条件的限制下，求线性目标函数最大或最小的问题[10]。决策变量、约束条件、目标函数是线性规划的三要素。在解决实际问题时，把问题归结成一个线性规划数学模型是很重要的一步，但往往也是困难的一步，模型建立得是否恰当，直接影响到求解。而选取适当的决策变量，是建立有效模型的关键之一。

本研究采用线性规划方法，对区域规划的规划结构进行建模，可以解决规划中的规划结构优化问题。具体为：以区域规划的人口经济收益最大化为目标函数，以规划的各产业规模为变量，以区域水资源、耕地面积、粮食产量、污染物排放量为约束条件，通过线性优化分析，可以对区域规划的产业规模结构进行优化，在不突破区域资源环境承载力的情况下实现人口经济目标最大化(称为规划模型一)；以区域规划的资源环境利用效率系数(单位GDP用水系数、单位GDP污染物排放系数、单位GDP耕地利用及粮食产量系数等)最优为目标函数，以规划的各产业资源环境利用系数为变量，分别以区域水资源、耕地面积、粮食产量、污染物排放量为约束条件，最终得出资源环境承载力约束范围之内的单位GDP资源环境利用系数等优化值(称为规划模型二)。

1.2 MATLAB GUI 方法

MATLAB是目前在国际上被广泛使用的计算机工具，是一种集数值与符号运算、数据可视化、图形用户界面设计、编程、仿真等多功能于一体的集成软件，具有功能强大、易于学习、应用广泛等特点。其图形用户界面(Graphical User Interface，GUI)是由窗口、光标、按钮、菜单、文字说明等对象构成的一个界面，它可以通过鼠标激活图形控件，使计算机产生某种动作，形成一个供反复使用且操作简单的专业工具[11]。本研究基于MATLAB自带LINPROG函数及GUI功能，实现了产业发展调控的程序封装。

1.3 案例数据方法

为初步验证在MATALB GUI环境下，基于资源环境承载力约束条件下的产业发展调控可视化的效果，本研究以云南某县城基础数据为依据进行程序验证，数据获取主要资料为：历年统计年鉴、历年水资源公报、土地利用总体规划、历年环境统计数据等。

表1 规划模型参数及变量含义一览表

2 结果与讨论

2.1 规划模型的建立

本研究的规划模型之一[7,12,13]为：双目标函数为经济和人口规模最大，约束条件为三产业的用水量必须小于用水总量控制线，污染物排放量(COD、氨氮、SO2、氮氧化物)必须小于该区域的实际环境容量，耕地面积、建设用地面积必须小于实际控制线，粮食产量必须大于最低粮食产量，居民生活质量必须大于最低生活质量保障。其模型表述如下：

MaxGDP=XP+Xs+Xt

≤TW

……水资源约束(1)

Cpxp+Csxs+Ctxt≤TCOD……COD

排放约束(2)

npxp+nsxs+ntxt≤TAN

氨氮排放约束(3)

spxp+ssxs+Stxt≤TSO2

SO2排放约束(4)

NPxp+NSxs+Stxt≤TNOχ

……NOx排放约束(5)

……耕地面积约束(6)

……建设用地面积约束(7)

……粮食产量约束(8)

……居民生活保障约束(9)

xp≥0；xs≥0；xt≥0

本研究的规划模型之二[6]为水资源约束条件下的单位GDP用水量系数最优化，其为：

Maxw=Wp+Ws+Wt

Wi≤Wp(Ws,Wt)≤Wu

污染物排放约束条件下的单位GDP排放量系数最优化，其为：

Max=Cp+Cs+Ct

Cpxp+Csxs+Ctxt+≤TC

Ct≤Cp(Cs,Ct)≤Cu

耕地面积、粮食产量、建设用地面积、居民生活保障约束条件下单位耕地面积及建设用地所能产生增加值、单位耕地面积粮食产量、人均GDP系数最优化，其为：

以上规划模型的变量及参数含义单位见表1。

表2 产业发展调控软件主程序

%双目标线性规划优化f1=[-1;-1;-1];%目标函数fori=1∶3%循环模式f21=-1/e(i)*Pp(i);f22=-1/e(i)*Ps(i);f23=-1/e(i)*Pt(i);f2=[f21;f22;f23];A11=Wp(i)+Wu(i)*0.001*u(i)*365/e(i)*Pp(i)+Wr(i)*0.001*365*(1-u(i))/e(i)*Pp(i);A12=Ws(i)+Wu(i)*0.001*u(i)*365/e(i)*Ps(i)+Wr(i)*0.001*365*(1-u(i))/e(i)*Ps(i);A13=Wt(i)+Wu(i)*0.001*u(i)*365/e(i)*Pt(i)+Wr(i)*0.001*365*(1-u(i))/e(i)*Pt(i);%水资源约束A21=-(1-PGDP(i)/e(i)*Pp(i));A22=-(1-PGDP(i)/e(i)*Ps(i));A23=-(1-PGDP(i)/e(i)*Pt(i));%居民生活保障约束A31=-0.50/ap(i);A32=0;A33=0; %耕地面积约束A41=-0.50*yp(i)/ap(i);A42=0;A43=0; %粮食产量约束A51=Cp(i);A52=Cs(i);A53=Ct(i);%COD约束A61=np(i);A62=ns(i);A63=nt(i);%氨氮约束A71=Sp(i);A72=Ss(i);A73=St(i); %SO2约束A81=Np(i);A82=Ns(i);A83=Nt(i); %氮氧化物约束A91=0;A92=1/Is(i);A93=0;%建设用地面积约束A=[A11,A12,A13;A21,A22,A23;A31,A32,A33;A41,A42,A43;A51,A52,A53;A61,A62,A63;A71,A72,A73;A81,A82,A83;A91,A92,A93];Ib=[0;0;0];ifi==1Aeq11=1;Aeq12=-Ra1(1);Aeq13=0;Aeq21=0;Aeq22=1;Aeq23=-Ra1(2);elseifi=2=Aeq11=1;Aeq12=-Ra2(1);Aeq13=0;Aeq21=0;Aeq22=1;Aeq23=-Ra2(2);elseifi=3Aeq11=1;Aeq12=-Ra3(1);Aeq13=0;Aeq21=0;Aeq22=1;Aeq23=-Ra3(2);endendend%不同产业比约束Aeq=[Aeq11,Aeq12,Aeq13;Aeq21,Aeq22,Aeq23];beq=[0;0];[x1,fval]=linprog(f1,A,b,Aeq,beq,Ib,[])%求GDP目标最大值XG(:,i)=x1;%GDP目标下的三产增加值优化值XGt(i)=fval;%最大GDP值[x2,fval2]=linprog(f2,A,b,Aeq,beq,Ib,[])%求人口目标最大值XP(:,i)=x2;%人口目标下的三产增加值优化值XPt(i)=fval2;%最大人口数

2.2 产业发展调控可视化

基于2.1节的规划模型的建立，首先利用MATLABGUI功能新建相关可视化窗口见图1，点击“进入”按钮进行输入参数及输出窗口的设置(部分展示见图2)。其中，主程序的编写在“计算”按钮里，部分程序见表2[14]。

2.3 案例分析与应用

通过规划模型的建立及产业发展调控可视化，基于云南某县城的统计数据，得出模型的部分输入参数数据见表3(模式一)。为了验证模式的正确性，现通过增加单位耕地面积所能产生增加值、单位耕地面积粮食产量、第一产业单位增加值用水量等参数(见表3模式二和模式三)。

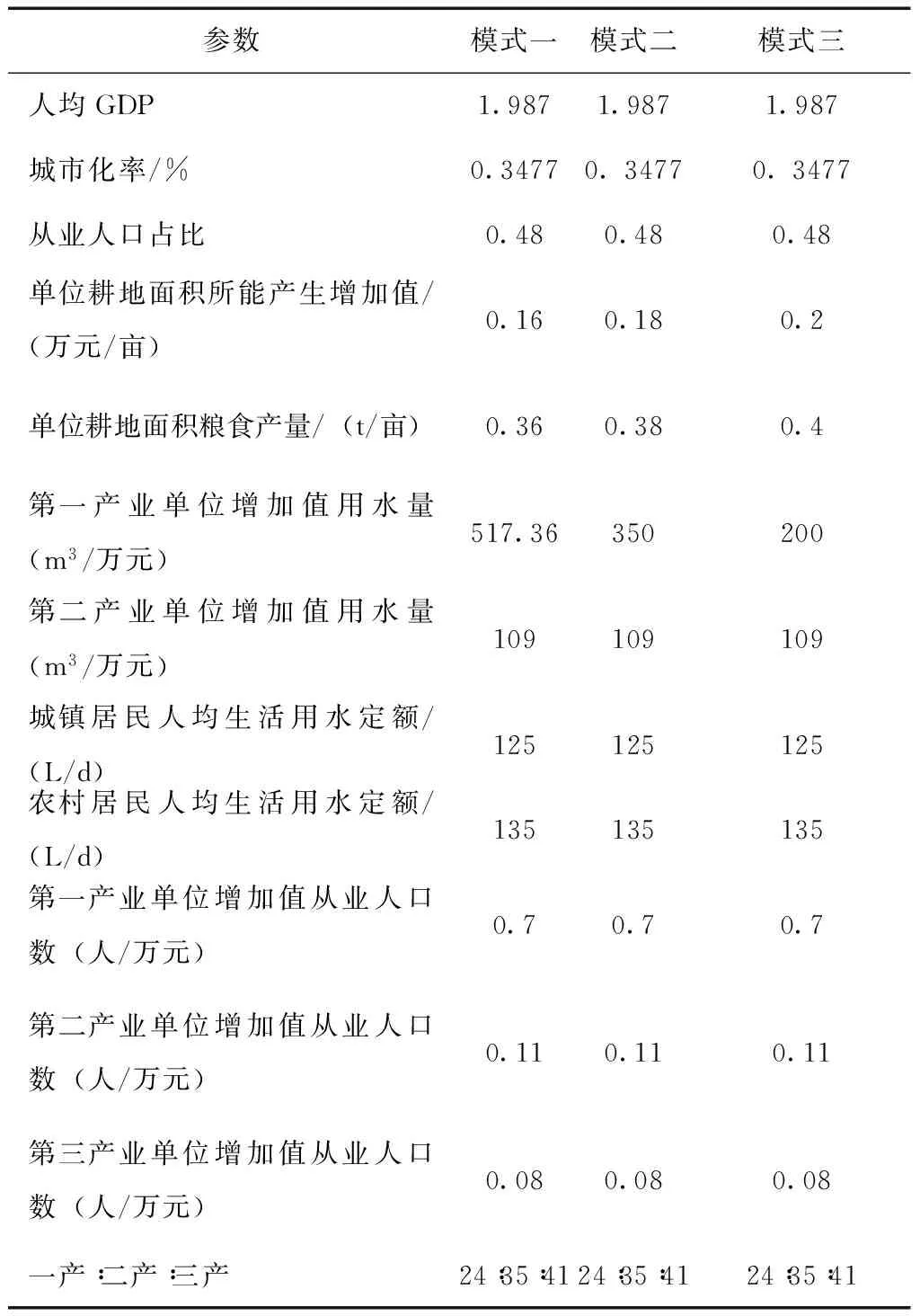
表3 案例分析验证部分参数

运行模型后，部分结果显示：在人为增加耕地利用系数、第一产业用水量系数及减少排污系数的条件下，其在资源环境承载力范围之内，能容纳的人口和经济规模逐步增大(见图3)；在加大GDP规模(一产、二产、三产产值相应增大)的情况下，其在COD排放容量限制范围内，不同产业的COD排放系数需相应减小，以便满足GDP的进一步发展(见图4)。

3 结论

(1)通过MATLABGUI功能，建立了完整的基于资源环境承载力约束的产业发展调控规划模型之一：以产业增加值为变量，以资源环境承载力为约束条件，以人口和经济最大化为目标函数。通过案例验证，模型应用可靠。

(2)通过MATLABGUI功能，分别建立了全面的基于资源环境承载力约束的产业发展调控规划模型之二：分别以资源环境利用系数为变量，以资源环境承载力为约束条件，以资源环境利用系数最大化为目标函数。通过案例验证，模型应用可行。

(3)通过MATLABGUI功能建立的基于资源环境承载力约束的产业发展调控可视化，将在一定程度上为区域环境规划决策提供理论基础及实践参考。

[1]任一鑫, 盖丽, 王伟. 资源环境承载力约束下产品结构优化方法研究[J]. 荆楚学刊, 2015, 16(5): 45-50.

[2]时进钢, 王亚男, 祝晓燕, 等. 基于资源环境承载力的规划结构优化方法探讨[J]. 环境科学与技术, 2010, 33(9): 187-191.

[3]郭健, 江明. 资源环境承载力研究在城乡总体规划中的应用——以河北省武安市为例[C]. 昆明: 中国城市规划年会论文集, 2012 .

[4]顾晨洁, 李海涛. 基于资源环境承载力的区域产业适宜规模初探[J]. 国土与自然资源研究, 2010(2): 8-10.

[5]马仁锋, 王筱春, 易琦, 等. 资源环境约束下的昆明都市区发展模式[J]. 复旦学报(自然科学版), 2010, 49(1): 104-115.

[6]冉芸. 基于水环境承载力的区域产业发展战略调控分析研究 [D]. 北京:清华大学, 2010.

[7]温鑫. 基于IFMOP模型的四平市水环境承载力及环境经济系统综合规划研究 [D]. 吉林：吉林大学, 2015.

[8]宗节保, 段柳云, 王莹, 等. 基于MATLABGUI软件制作方法的研究与实现[J]. 电子设计工程, 2010, 18(7): 54-56.

[9]张志涌, 杨祖樱.MATLAB教程[M]. 北京: 航空航天大学出版社, 2010:23-28.

[10]束金龙,闻人凯. 线性规划理论与模型应用[M]. 北京: 科学出版社,2003:34-42.

[11]杨德平. 经济预测模型的MATLABGUI开发及应用[M]. 北京: 机械工业出版社, 2015:1-2.

[12]AHMADIP,DINCERI,ROSENMA.Thermodynamicmodelingandmulti-objectiveevolutionary-basedoptimizationofanewmultigenerationenergysystem[J].EnergyConversionandManagement, 2013( 76): 282-300.

[13]GUANZ,PHILPOTTAB.AmultistagestochasticprogrammingmodelfortheNewZealanddairyindustry[J].InternationalJournalofProductionEconomics, 2011, 134(2): 289-99.

[14]GoodarziE,ZiaeiM,HosseinipourEZ.OptimizationAnalysisUsingLINGOandMATLAB[M].NewYork:SpringerInternationalPublishing, 2014:149-193.

The Visualization of Industry Development Regulation based on the MATLAB GUI

WANG Wan-bin, LI Sen, ZHANG Xing-zi, REN Jing, JIA Hai-feng, CHEN Yi -hui

(Yunnan Institute of Environmental Science, Kunming Yunnan 650034, China)

The visualization of industry development regulation would provide a basis for environmental planning to make effective decision under the carrying capacity of resources and environment. In this study, firstly, the planning models with the maximum total output value of population and economy were built up. Some parameters of consumption of resources and environment(e.g. the quantity of water consumption and pollutant discharge each added-value of industrial output) have been determined under the constraint condition of water resources, land resources (plough, construction land, environmental capacity of pollutant (COD、NH4-N、SO2、NOx) and grain output. Then, the visual simulation was achieved using the function of MATLAB GUI. The visualization of industry development regulation based on the MATLAB GUI has been verified by a simple and practical example.

MATLAB; GUI; industry development regulation; carrying capacity of resources and environment; visualization

2016-10-12

王万宾(1988-)，男，硕士研究生，主要研究方向为资源环境承载力分析与产业发展调控。

X321

A

1673-9655(2017)03-0018-06