不同出口角度扩压器的内部流动及离心压缩机级性能数值研究

赵志伟, 苏永升(华东理工大学承压系统与安全教育部重点实验室,上海 200237)

不同出口角度扩压器的内部流动及离心压缩机级性能数值研究

赵志伟, 苏永升
(华东理工大学承压系统与安全教育部重点实验室,上海 200237)

以某多级离心压缩机首级为研究对象,运用数值模拟方法研究扩压器出口安装角对压缩机级性能的影响,得出不同出口安装角情况下压缩机单级的性能曲线,并分析扩压器内部流动特点和损失机理,通过压力恢复系数Cp对比不同流量下不同扩压器的扩压效果。结果表明,当扩压器出口安装角增大时,性能曲线向大流量区移动,最高效率和压比先升高后降低;不同出口角度下叶片扩压器的扩压效果由不同工况下的流动特性决定;在大流量下,不同出口角度下扩压器叶背形成分离区且旋涡位置不同;在小流量下,具有较大出口安装角的扩压器叶腹率先出现分离区。

叶片扩压器; 出口安装角; 性能曲线; 压力恢复系数

离心压缩机由于结构紧凑、工艺性好及性能高,在国民经济中占有重要地位,长期以来很多学者对离心压缩机的气动特性进行了研究[1]。在离心压缩机所有静止件中,扩压器属于核心部件,对提高压缩机效率和级压比、改善最佳工况点十分重要[2]。针对扩压器的研究已有大量的文献。周俊安等[3]研究带叶片扩压器离心压缩机模型级内流,得出扩压器内的流动损失和扩压效果由不同工况下的流动特性决定;席光等[4]通过数值与实验研究表明叶片扩压器进口安装角对压缩机流动有较大影响;王志恒等[5]以高压比离心压缩机级性能为研究对象,研究了扩压器进口安装角和叶型对级性能的影响。李学臣等[6]采用数值模拟对多级离心压缩机中间级的流动进行了研究,重点考察进口段、弯道和回流器对中间级气动性能的影响;Anish等[7]采用数值模拟方法分析了不同扩压器、叶轮与扩压器不同间隙情况下离心压缩机的性能;Zheng等[8]建立理论分析模型准确地预测出扩压器的阻塞流量,证明随着进口预旋角增大,扩压器的阻塞流量比叶轮阻塞流量下降缓慢。Bousquet等[9]通过数值模拟质量流量减少对叶轮和扩压器进口的影响,提出详细的失速机理。

本文以多级离心压缩机首级作为研究对象,采用流体计算软件CFX数值模拟扩压器在不同出口角度情况下的级性能曲线,对比扩压器压力恢复系数Cp,详细分析了叶片扩压器出口安装角对压缩机内部流场特点、损失机理及级性能的影响。

1 几何模型与网格

1.1 几何模型

离心压缩机首级由进口段、后弯闭式叶轮、叶片扩压器、弯道和回流器组成,叶轮叶片和扩压器叶片均采用等厚度型,叶轮及扩压器流道结构如图1所示,设计参数如表1和表2所示,其中叶轮转速为8 000 r/min,进口总温度为20 ℃,进口总压为0.101 MPa,介质为空气,相对宽度为叶片出口宽度与叶轮外径之比,β2A为叶轮叶片出口安装角,α3A和α4A分别为扩压器进口、出口安装角。

图1 叶轮及扩压器流道结构

Outerdiameter/mmNumbersofbladeRelativewidthβ2A/(°)600200．07345

表2 叶片扩压器设计参数

1.2 计算网格及无关性验证

为全面考察扩压器出口安装角对上下游部件流动的影响,采用整级数值模拟,所选计算区域包括进口段、叶轮、叶片扩压器、弯道和回流器。采用ICEM前处理软件,生成全场四面体非结构化网格。通过选用网格拓扑模块实现网格拓扑的自动管理、网格优化、网格块的附着和关联等功能,提高网格的质量和效率。同时加密靠近壁面的网格以满足湍流模型对y+的要求。本文采用全流道计算,计算域及网格如图2所示。

在数值模拟计算时,所有模型级的网格数均满足无关性要求。图3示出了在质量流量为7.25 kg/s时扩压器Ⅱ的网格无关性验证。由图3可知级效率(η)与压比(ε)变化不明显,认为网格达到无关性。考虑到求解精度和计算速度,采用表3所示的扩压器网格计算分析,整级的网格数大于2.7×106。

图2 计算域及网格

图3 网格无关性验证

No．NumbersofgridNodesⅠ1175821204597Ⅱ1178060204853Ⅲ1179426205006Ⅳ1179040204852

2 数学模型与边界条件

2.1 计算模型

应用流体计算软件CFX来求解三维可压缩雷诺平均守恒型N-S方程。湍流模型选取κ-ε两方程模型[10],壁面边界层效应采用壁面函数法。为保证求解准确,采用高阶求解模式。数值模拟控制方程可表示为方程(1)通用形式:

(1)

式中:ρ为密度;V为体积;t为时间;φ为通用变量;Γ为广义扩散系数;S为广义源项。

2.2 边界条件及收敛标准

本文计算过程分为定常计算和非定常计算两个阶段。为有效减少流动不充分所带来的误差,进口边界设置为进口段入口,出口边界为回流器出口。定常计算的计算域入口均为给定总温、总压和轴向速度方向;出口为质量流量;固体壁面均为绝热、无滑移条件。非定常计算以定常计算结果为初始流场,柯朗数CFL取2,时间步长设置为2.3×10-4s,内迭代设置为20步。计算残差下降到10-4数量级以下,当进出口流量误差小于0.1%,其他监控参数(效率和压比)保持恒定时,即认为计算收敛。

3 数值模拟结果分析

3.1 性能曲线

图4、图5分别示出了不同质量流量(Qm)下级压比和多变效率曲线。由于当质量流量小于5.75 kg/s时,整级模拟不能收敛,所以数值模拟从质量流量为5.75 kg/s开始计算;当质量流量大于5.75 kg/s并小于7.00 kg/s时,定常计算难以收敛,此时以定常计算结果为初始流场,采用非定常计算。非定常计算结果在本文中采用时均值处理[11]。

图4 压比曲线

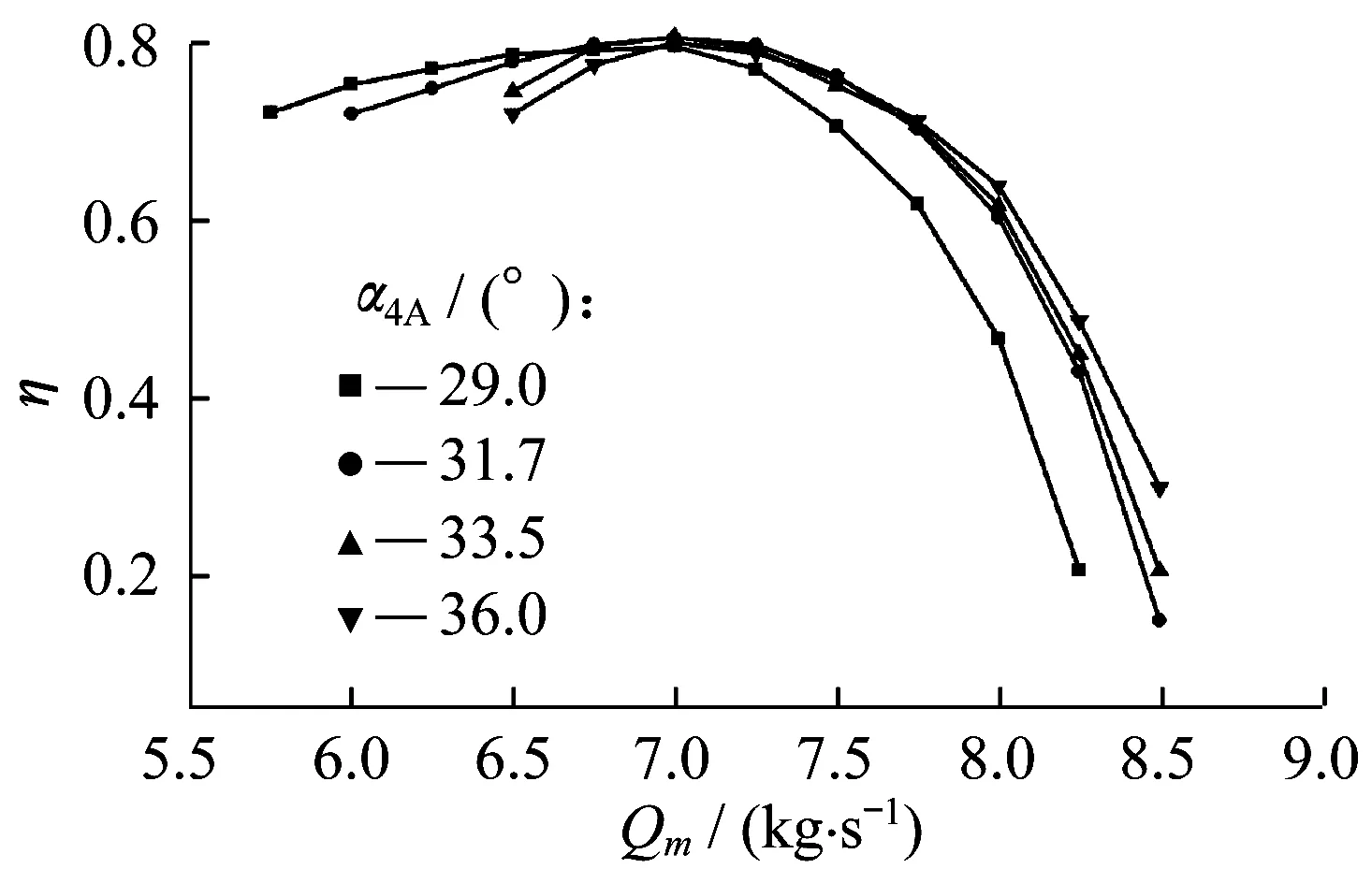
图5 效率曲线

如图4、图5所示,随着扩压器出口安装角度增大,级性能曲线向大流量方向偏移,虽最高效率和压比先升高后降低，但它们的最高值提升并不明显,且最大工况点变化不大。在设计质量流量7.25 kg/s附近工况点,带有4种不同出口安装角的扩压器的压缩机级压比、效率接近;在质量流量为6.50 kg/s时,扩压器Ⅳ (α4A=36.0°)的离心压缩机级压比、效率明显下降;在质量流量为8.15 kg/s时,扩压器Ⅰ (α4A=29.0°)的级压比、效率都较低。通过性能曲线对比可以得出:当扩压器进口安装角度一定时,选取合适的出口安装角度既可以增大工作范围,又可以改善压缩机的工作效率。

3.2 扩压器内部流动分析

3.2.1 概述 本文采用3种工况,即质量流量分别取6.50、7.25、8.15 kg/s,分析扩压器内部的流动情况和压力损失。

3.2.2 扩压器等半径截面上Cp分析 扩压器的作用是将动能转化为静压力能。当考察扩压器性能时,采用静压恢复系数Cp[12]也是一种判定方法。定义静压恢复系数为

(2)

其中:Ps3,Psx分别为扩压器叶片前缘进口、等截面的静压平均值;Pt3为扩压器叶片前缘进口总压的平均值。

图6～图8示出了不同工况下扩压器静压恢复系数分布。

如图6,当质量流量为6.50 kg/s时,不同出口安装角度的扩压器在扩压器出口处都有较高的静压恢复系数,但扩压器Ⅳ的静压恢复系数相比于其他扩压器较低,其次较低的是扩压器Ⅰ,扩压器Ⅱ和扩压器Ⅲ的静压恢复系数相近。

图6 Qm=6.50 kg/s时扩压器静压恢复系数

当质量流量为7.25 kg/s时(如图7),扩压器Ⅱ、Ⅲ、Ⅳ的静压恢复系数良好,而扩压器Ⅰ的静压恢复系数相比其他扩压器较低。此时,随着扩压器出口安装角度的增大,扩压器静压恢复系数增大。

当质量流量为8.15 kg/s时(如图8),静压恢复系数出现较大差异,扩压器流道中静压恢复系数为负值。且随着出口安装角的增大，极小值向出口处偏移。在扩压器出口处，扩压器Ⅰ的静压恢复系数为负值,失去扩压器功能；扩压器Ⅱ的静压恢复系数为零,也失去扩压功能,扩压器Ⅲ、Ⅳ的静压恢复系数为正值,有部分扩压功能。

综合图6～图8可见,在小流量和设计流量时,扩压器静压恢复系数在前半段上升较快,后半段变平缓,说明扩压器的扩压功能主要集中在前半段;在大流量时,出口安装角度小的扩压器率先失去扩压功能。

图7 Qm=7.25 kg/s时扩压器静压恢复系数

图8 Qm=8.15 kg/s时扩压器静压恢复系数

3.2.3 扩压器50%叶高截面处静压和流线分布 在稳态流动时,流线的形状和位置不随时间变化,采用流线能直观反映流动情况,同时静压云图可直观反映扩压器内静压力分布。下文以扩压器Ⅰ、Ⅱ(与Ⅲ相近)、Ⅳ作为研究对象,分析了扩压器50%叶高截面处流体流动情况和压力分布。当质量流量为6.50 kg/s时,由于计算结果为非定常计算所得,故小流量采取时均处理。

当质量流量为6.50 kg/s时(如图9),扩压器叶片前缘冲角i=6°,扩压器内流动出现差异。扩压器Ⅰ并未产生旋涡区,而扩压器Ⅱ叶腹尾缘产生较小旋涡区,但扩压器Ⅱ有较高的静压;扩压器Ⅳ叶腹尾缘处产生较大分离和回流,形成气流旋涡,同时部分流道由于旋涡的存在静压分布不均匀。

当质量流量为7.25 kg/s时(如图10),扩压器叶片前缘冲角i≈0°,气流分布均匀且速度变化平缓,没有明显的气流分离或回流,流动情况良好。此时扩压器Ⅱ、Ⅳ有较高的静压。

图9 Qm=6.50 kg/s时50%叶高截面处静压和流线时均图

图10 Qm=7.25 kg/s时50%叶高截面处静压和流线图

当流量为8.15 kg/s时(如图11),扩压器叶片前缘冲角i=-8°,扩压器Ⅰ、Ⅱ、Ⅳ叶背都产生明显旋涡,而扩压器Ⅰ旋涡主要出现在叶背前缘,且在喉部流动变为收敛性质;扩压器Ⅳ产生的旋涡位于叶背靠近出口处且旋涡偏小,扩压器Ⅱ介于两者之间。扩压器静压都明显下降,同时在叶片前缘处产生较大的冲击损失。

图11 Qm=8.15 kg/s时50%叶高截面处静压和流线图

3.2.4 扩压器等半径截面的总压分布 扩压器内的总压分布反映内部流动损失的分布,且等半径截面的总压分布能全面地反映出扩压器周向与径向的流动损失分布。图12～图14示出了不同工况下扩压器Ⅰ、Ⅱ、Ⅳ沿气体流向在半径截面上的总压分布,其量纲为一半径分别为X1=0.2、X2=0.5和X3=0.8。图中S、H、SS、PS分别表示扩压器的前盖板、后盖板、吸力面和压力面。

当质量流量为6.50 kg/s时(如图12),由于气流进气角度偏小,气流向叶背靠拢,在靠近叶背处产生较大的总压,且轮盖侧高于轮盘侧,而靠近叶腹的总压急剧减小。扩压器Ⅳ沿周向总压梯度变化比较大且在X3截面上靠近叶腹的总压低,产生流动损失,其次是扩压器Ⅱ、Ⅰ。

当质量流量为7.25 kg/s时(如图13),扩压器各截面内总压梯度变化小,但也有差异;扩压器Ⅰ较其他二者总压梯度变化大,扩压器Ⅱ在流道内流动尤其平稳;扩压器Ⅱ、Ⅳ在X3截面的压力已分布均匀。扩压器Ⅰ、Ⅱ、Ⅳ未产生总压明显减小的区域,说明此工况下扩压器内的流动损失小。

当质量流量为8.15 kg/s时(如图14),由于气流进气角度偏大,气流不断向叶腹靠拢,在叶腹靠近轮盖侧总压局部上升;而在叶背处总压急剧减小产生分离,流动损失较大,总压沿周向和径向分布都不均匀。扩压器Ⅰ在X1截面叶背处存在明显低压区,而扩压器Ⅱ在X2截面叶背处存在明显低压区,扩压器Ⅳ在X2截面存在低压区且随着截面半径的增大低压区范围扩大。

图13 Qm=7.25 kg/s时扩压器Ⅰ、Ⅱ、Ⅳ沿流向各半径截面上的总压分布图

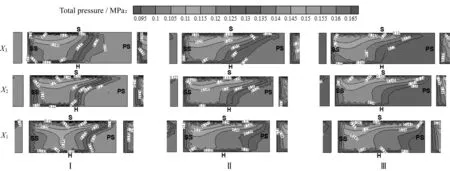
图14 Qm=8.15 kg/s时扩压器Ⅰ、Ⅱ、Ⅳ沿流向各等半径截面上的总压分布图

综合图12～14可知,小流量(6.50 kg/s)和设计流量(7.25 kg/s)下，扩压器Ⅰ、Ⅱ、Ⅳ总压损失并不明显,表明叶腹产生的旋涡对总压影响并不大;而大流量(8.15 kg/s)下总压损失较前两种工况大,表明分离损失产生的旋涡对总压损失的影响较大。

4 结 论

(1) 数值研究表明,当扩压器叶片出口安装角度增大时,级性能曲线向大流量方向移动,级最高效率和压比先升高后降低;对某一流量应存在最佳的出口安装角度,使级性能最优。

(2) 扩压器静压恢复系数在扩压器前半段上升较快,后半段变平缓。小流量下扩压器的扩压效果随出口角度的增大先增强后减弱;设计流量下扩压器扩压效果随出口角度的增大而增强;大流量下扩压器中间段不起扩压效果,丧失部分扩压功能,且出口安装角度小的扩压器率先失去扩压功能。研究表明不同出口安装角叶片扩压器的扩压效果由不同工况下的流动特性决定。

(3) 就单级流动特性而言,小流量下出口安装角度大的扩压器叶腹率先出现分离区,叶腹出现的旋涡对总压损失影响较小;大流量下不同出口角度的扩压器其叶背形成分离区且旋涡的位置不同,叶背出现的旋涡对总压损失影响较大。

[1]孙涛,王毅等.变厚度叶片对离心压缩机结构强度和性能影响[J].大连理工大学学报,2012,52(1):29-34.

[2]徐玉梅,刘丹丹,谢俊良,等.宽窄扩压器失速机理模拟分析[J].轻工机械,2015,33(3):33-37.

[3]周俊安,刘立军,肖萍,等.带叶片扩压器离心压缩机模型级内流研究[J].西安交通大学学报,2015,49(9):1-6.

[4]席光,周莉,丁海萍,等.叶片扩压器进口安装角对离心压缩机性能影响的数值与实验研究[J].工程热物理学报,2006,27(1):61-64.

[5]李学臣,席光,李心伟,等.离心压缩机中间级内流动数值研究[J].工程热物理学报,2010,31(6):955-958.

[6]王志恒,张鲲羽,王宏亮,等.叶片扩压器对离心压气机整机性能影响的实验及数值研究[J].工程热物理学报,2015,36(10):84-88.

[7]ANISH S,SITARAM N.Computational investigation of impeller-diffuser interaction in a centrifugal compressor with different type of diffusers [J].Proceeding of the Institution of Mechanical Engineers:Part A.Journal of Power and Energy,2009,223(A2):167-178.

[8]ZHENG Xinqian,HUANG Qiangqiang,LIU Anxiong.Loss mechanisms and flow control for improved efficiency of a centrifugal compressor at high inlet prewhirl[J].Journal of Turbomachinery,2016,138(10):101011-1-11.

[9]BOUSQUET Y,BINDER N.Numerical simulation of stall inception mechanisms in a centrifugal compressor with vaned diffuser[J].Journal of Turbomachinery,2016,138(12):121005-1-9.

[10]陶文铨.数值传热学[M].第2版.西安:西安交通大学出版社,2011:347-353.

[11]BENICHOU E,TRÉBINJAC I.Comparison of steady and unsteady flows in a transonic radial vaned diffuser[J].Journal of Turbomachinery,2016,138(12):121002-1-10.

[12]FILIPENCO V G,DENIZ S,JOHNSTON J M,etal.Effects of inlet flow field conditions on the performance of centrifugal compressor diffusers:Part 1.Discrete-passage diffuser [J].Journal of Turbomachinery-Transactions of the Asme,2000,122 (1):1-10.

Numerical Study of the Different Outlet Angles of Diffuser and Performance of Centrifugal Compressor

ZHAO Zhi-wei, SU Yong-sheng

(Key Laboratory of Pressurized Systems and Safety,Ministry of Education,East China University of Science and Technology,Shanghai 200237,China)

Based on the first stage of centrifugal compressor ,the effects of outlet angles of diffuser on the stage performance were investigated by the numerical simulation.The performance curves at stage with different outlet angle were measured.The internal flow and the total pressure loss on the stage were analyzed,and by comparison of pressure recovery coefficient of different vaned diffusers to judge diffusion effect.The results show that the increase of outlet angle makes the performance curve move toward the large flow rate side,and the peak stage efficiency and pressure ratio increase firstly and then decrease.The diffusion effect of vaned diffuser depends upon flow condition during different operations.When the flow mass is larger than the design level,the separation zone generates near the shroud of diffuser,and the different vortex regions enlarge with the outlet angle of diffuser.When the flow mass is smaller than the design level,the separation zone is firstly emerged in large outlet angle at vaned diffuser.

vane diffuser; outlet angles; performance map; pressure recovery coefficient

1006-3080(2017)02-0266-07

10.14135/j.cnki.1006-3080.2017.02.019

2016-06-21

赵志伟(1989-),男,山西人,硕士生,从事流体机械方向研究。E-mail:zhaozhiwei012@126.com

苏永升,E-mail:yssu@ecust.edu.cn

TH452

A