基于BA无标度网络的WSNs拓扑优化模型
2017-04-27路智静孙俊峰华东理工大学信息科学与工程学院上海200237
路智静, 黄 如, 孙俊峰, 张 磊(华东理工大学信息科学与工程学院,上海 200237)
基于BA无标度网络的WSNs拓扑优化模型
路智静, 黄 如, 孙俊峰, 张 磊
(华东理工大学信息科学与工程学院,上海 200237)
由于无线传感器能量受限,最大化网络生命周期成为优化网络拓扑首要考虑的问题。基于BA无标度理论,提出了一种WSNs拓扑优化模型(WTOM)。在网络中引入超级节点,结合粒子群算法合理地划分整个网络;在节点间建立多因素为导向的虚拟力场,利用虚拟力调整超级节点的部署位置,实现网络能量的均衡消耗,通过对关键节点的保护,提高网络的抗毁鲁棒性。经理论分析和实验证明,该网络不仅继承了BA无标度网络的特征还具有小世界特性;同时该动态拓扑延长了网络的生命周期,提高了网络面向数据收集的节能性。
无线传感网络; BA无标度网络; 拓扑优化; 超级节点
随着微电子技术、通信技术和计算机技术的飞速发展,无线传感网路(WSNs)在军事和民用各个领域都得到广泛应用[1],然而无线传感器节点受到部署环境限制,其能量不能得到及时补充。合理、高效的拓扑优化能够实现网络能量的均衡消耗和延长网络的生命周期。而复杂网络理论为建立可靠、高效的无线网络拓扑模型提供了一种新的研究思路和方法。Wang等[2]通过对度分布熵的优化来调整无标度网络结构,提升无标度网络抗随意性攻击能力进而优化网络的生命周期,但该拓扑模型没有考虑能量消耗不均衡问题。文献[3]在构建网络拓扑时通过控制网络节点饱和度和剩余能量等因素,提高了WSNs的抗毁性,延长了网络生命周期,但是在拓扑模型构建时没有考虑节点负载量,负载量高的节点会因耗能过快造成过早死亡,缩短网络生命周期。Tao等[4]统计自同构群的对称网络轨道,提出通过优化网络拓扑对称,使网络更趋于同步,该方法更侧重对网络模型同步性的研究,且没有用到复杂网络理论。文献[5]在 BA无标度网络基础上提出了新的 WSNs拓扑结构演化模型,该模型对节点的随机故障及失效具有较高的鲁棒性,但对网络模型具体特征没有作出分析。文献[6]利用小世界模型的聚类特性和边界数的概念对 WSNs 进行拓扑优化,并在此基础上引入了阈值机制,使网络优化之后具有较高的聚类系数、较明显的簇群结构,但平均路径长度变化不大。文献[7]在复杂网络理论的基础上,提出了一种新的加权局域 WSNs 演化模型在沙漠治理维护中的应用研究,推导出其度分布、强度分布、边权重分布均满足幂率分布特征,但没有考虑到网络拓扑的动态变化。文献[8-10]在复杂网络模型演化的过程中考虑了节点剩余能量对网络增长的影响,但对网络模型的抗毁性没有作出分析。Zhu等[11]基于局域网世界(Local world)模型,分别提出了两种无标度网络模型(EAEM模型和EBEM模型)。在EAEM模型中,新节点优先连接能量高的节点;而在EBEM模型中,除考虑剩余能量以外,新节点优先连接度较高的节点,但没考虑网络拓扑的变化。本文提出了一种基于BA无标度理论的WSNs拓扑优化模型,以最大化网络生命周期为目标,在网络初始演化的过程中构造节点适应度函数,考虑了网络剩余能量和节点度的共同影响。在网络拓扑动态优化的过程中,通过粒子群算法合理分区处理,利用节点度、节点剩余能量、节点密度多因素主导的虚拟力对超级节点的移动和部署进行优化,提高网络能量均衡消耗能力,实现关键节点的目标性保护。实验证明该网络还具有BA无标度特征和小世界特性的双重特点。
1 系统模型
1.1 概述
无线传感器网络中普通节点易受到环境的限制无法充电,某些节点由于能量的过度消耗而过早死亡,影响了网络的性能和生命周期。在网络中可以尝试添加能量高、储存容量大、数据通信能力强的超级节点来改善网络的拓扑特性。图1示出了WSNs拓扑优化模型(WTOM)示意图,如图所示,普通节点分布在超级节点的周围,按照WTOM模型初始化生成算法形成类似于蜘蛛网状的结构。模型中sink节点是路由信息的目的地,超级节点具有较大的通信半径。由于普通节点通信半径的限制,远离sink节点的普通节点最优选择通过超级节点将信息传递给sink节点。本模型中超级节点与普通节点按照一定比例加入网络中,网络中超级节点的个数将直接影响网络的整体性能。超级节点因为其自身的优势会更优先连接网络新加入的节点,同时超级节点也会影响其邻居节点与新加入节点的连接。超级节点类似于小世界效应,现实网络中都有这种现象。以文献检索为例,新的手稿往往引用本领域的经典文献,曾引用过本领域经典文献的文章,更容易受到新手稿的引用。
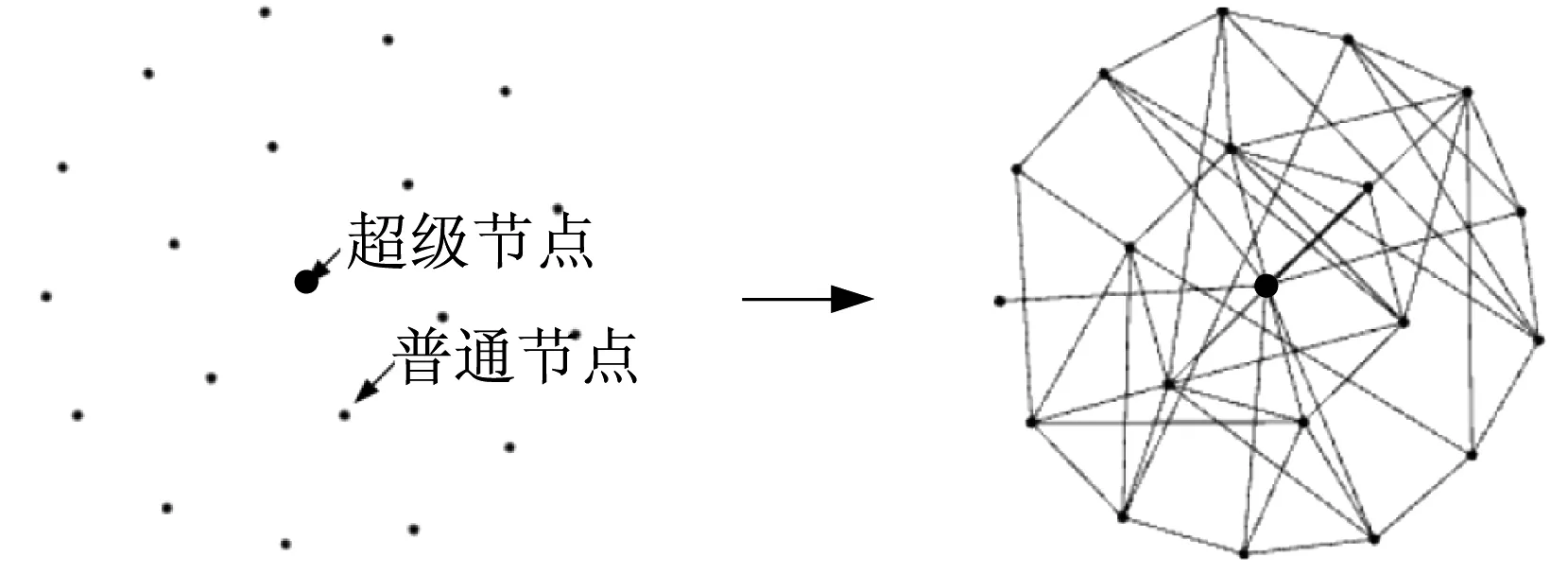
图1 WTOM模型图
1.2 模型前提假设
假设WSNs中随机分散着N个节点,它们具备如下特点:
(1) 传感器节点具有全局唯一的标识符ID。
(2) 普通传感器节点部署到目标区域内不具有移动能力,随机分布在正方形区域;超级节点具有移动能力;sink节点不具有移动能力,位于全局的中心。
(3) 在部署时,普通节点具有相同的能量;超级节点拥有几倍于普通节点的等同能量,且它们的能量均不能得到补充;sink节点的能量足够。
(4) 传感器节点不能获取地理位置信息,但能够根据信号的强度计算发送节点到本节点的相对距离。
1.3 相关定义
(1) 度ki与度分布p(k)。节点i的度ki定义为与i相连的节点的数目。网络中所有节点的度ki的平均值称为网络节点的平均度,记为
(1)
式中N为整个网络节点数。节点度分布用分布函数p(k)表示,p(k)表示在网络中随机选定的节点的度恰好是k的概率。
(2) 平均路径长度L。用L表示无线传感网络中所有节点发送数据到汇聚节点距离的平均跳数,Dj表示普通节点i到汇聚节点最短路径的跳数。
(2)
(3) 聚类系数C。聚类系数定义为i的ki个邻居间实际存在的连接数Ei除以节点i的邻居间完全连接的总连接数,表示与i相连的点中任意两点间相互连接的概率。
(3)
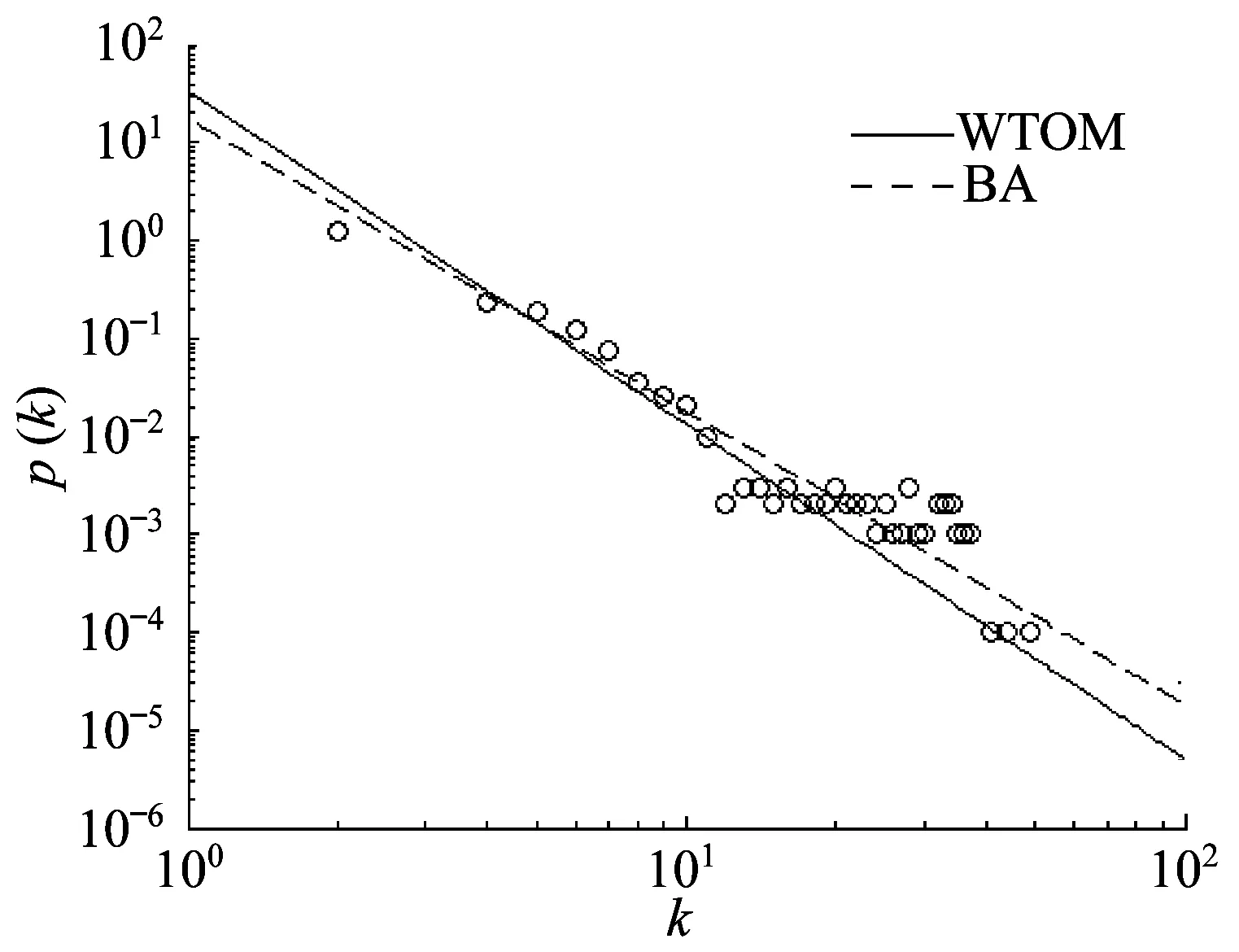
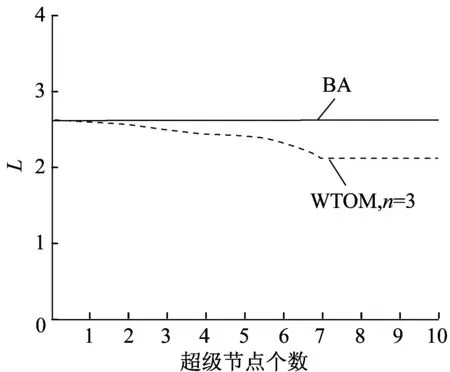
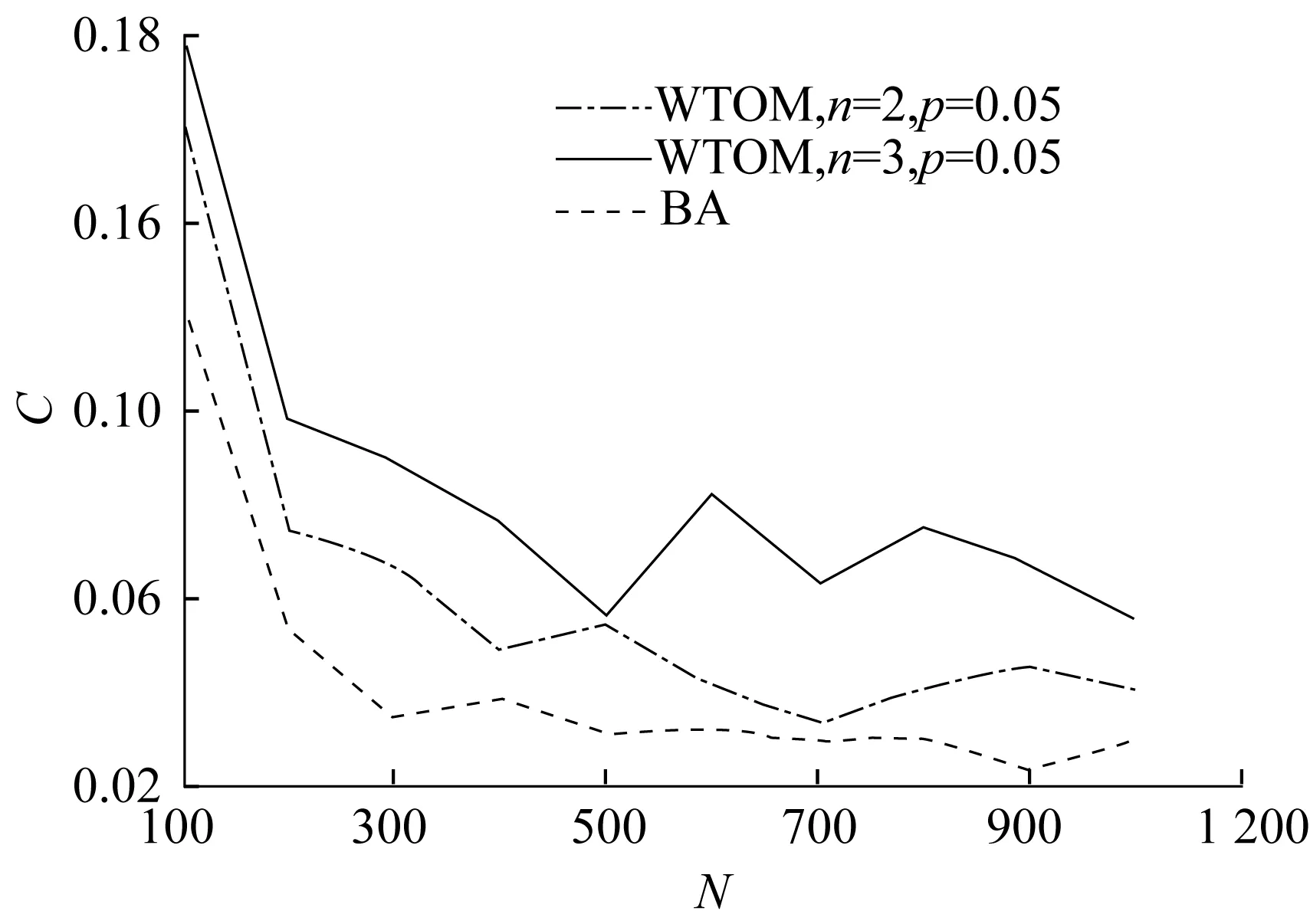
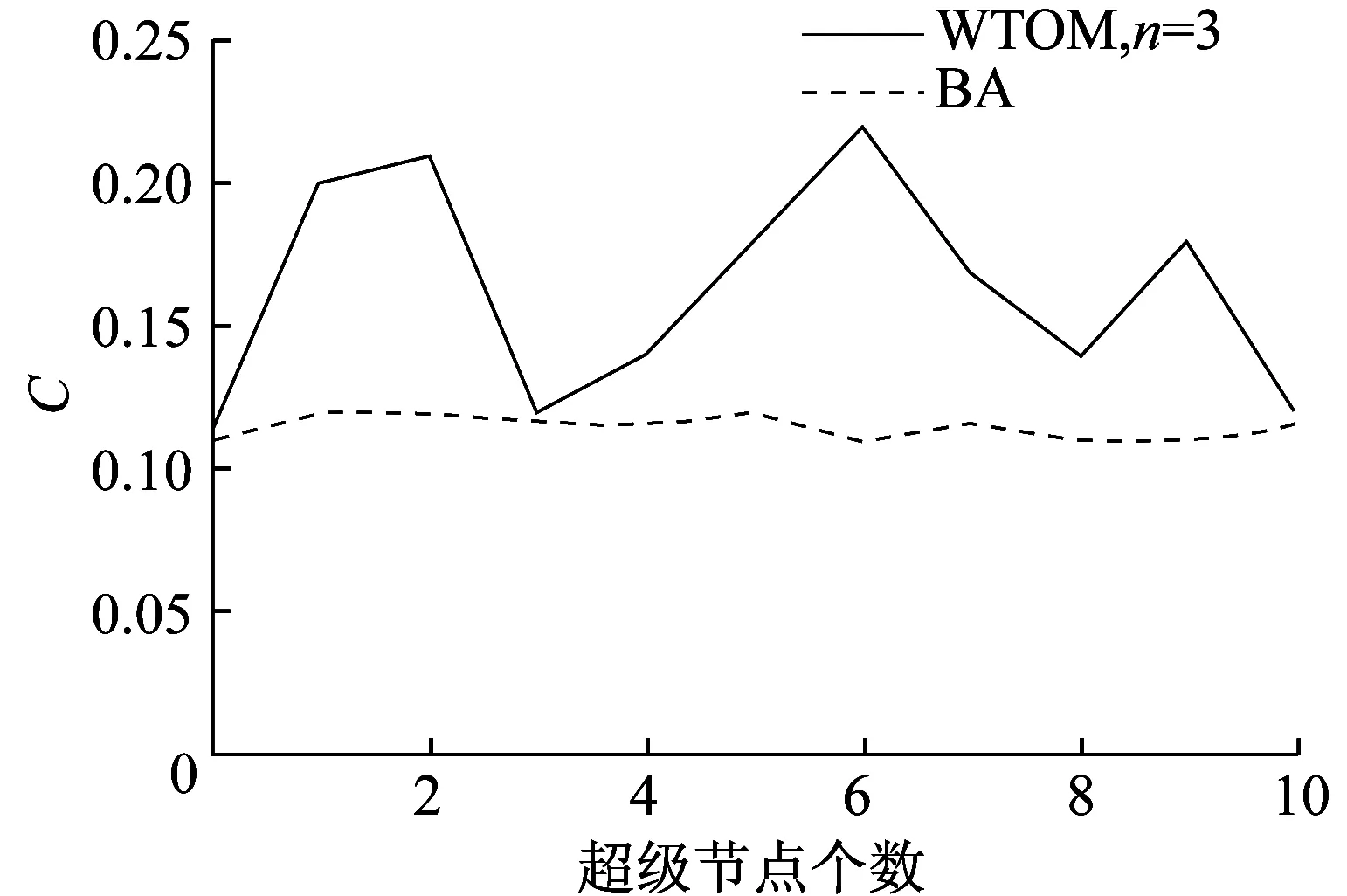
(4) 节点剩余能量与被选中连接关系f(E)。定义E表示剩余能量,f(E)表示节点剩余能量与被选中连接关系,节点的剩余能量越大,f(E)越大。当节点i为超级节点时,f(E)=nE,其中1 (5) WSNs生命周期。WSNs生命周期定义为网络中能量耗尽或失效节点超过总节点数一半之前正常通信的周期数。 1.4 网络拓扑动态优化机制 1.4.1 基于粒子群算法的网络分区 利用粒子群算法将整个网络中N个传感器节点分成a个区,其中a表示超级节点的个数,则每个区中含有N/a个节点。首先确定一条网络区域分割线,将网络分割成两个区域,两个区域内节点数目相同。分割线形式如下: (4) 式中:x,y分别为为位于分割线上点的横纵坐标;θ为分割线与x轴的夹角。 定义fitness函数如下: fitness=(d1-f1N)2+(d2-f2N)2 (5) 其中:di(i=1,2)为区域i中的节点数目;fi=ai/a(i=1,2),ai为期待超级节点的数目,即期待通过分割使得该区域保留多少个超级节点数。 (1) 对参数x,y,θ随机赋值,由式(4)确定区域分割线,至此整个区域被分成2个不同的子区域,把两个子区域节点的个数带入式(5)。 (2) 确定多个不同的fitness值,与上次搜索得到的最小fitness值进行比较并取最小值,与其对应的粒子作为全局极值Pgd;同理,比较单个粒子得到的fitness值取最小的作为个体极值Pid,令α分别取值为x,y,θ,然后通过式(6)更新x,y,θ。 (6) 其中:Xxid,Xyid为粒子的位置;Xθid为分割线的倾角;vxid,vyid,vθid为粒子在x,y,θ3个维度上的搜索速度,由式(7)确定。 (7) 其中:c1,c2为学习因子;w为权重因子。 (3) 粒子得到合适的x,y,θ后,代入式(4)转入步骤(1)的搜索,直到找到fitness值等于0或者近似0为止,此时,可以将整个区域分成节点数相等的两个部分。 (4) 将区域首次分割之后,对两个子区域继续分割,直到分成a个规模相等的区域结束。 1.4.2 以虚拟力为导向的超级节点部署调整 当节点i为超级节点时,为各超级节点找到邻近的子目标区域并调整其在子目标区域内的目标部署位置,在节点之间引入虚拟力,使超级节点在多因素影响的虚拟力作用下调整自身的部署位置。其中,各作用力取正数值时表示引力,取负数值时为斥力。 (1) 超级节点与同区域普通节点的作用力 (2) 子区域边界对超级节点的作用力 其中:Dj表示超级节点对应目标子区域的边界;|pi-Dj|是超级节点i距离重心Dj的距离;kbj是与两子区域相互位置关系相关的一个参数;kd是一个反映节点密度的增益系数,反映相邻子区域的节点密度与期望节点密度的关系;sn表示超级节点是否在目标区域内,若超级节点在目标区域sn取0,否则取1。 (3) 其他超级节点对超级节点i的作用力 其中:|pi-pj|为超级节点i,j之间的距离;d是一个固定值,为超级节点通信半径的1.71倍;kij是一个增益系数。 本文模型采用基于改进BA模型网络节点演化模型生成机制,并考虑到超级节点的影响,进而优化WSNs的网络拓扑。 (1) 起始设定。假设网络最初有m0个普通孤立节点,各普通节点储能量相同。 (2) 增长性。每个时间间隔加入一个新的节点v,新加入的节点v为超级节点的概率为p,为普通节点的概率为(1-p),其中0≤p≤0.1,每次加入的节点v新增的度为m(m (3) 确定局域世界。距节点v最短时间加入的M(M≥m)个节点作为节点v的局域世界,其中M是随时间增长的量,这M个节点均在节点v的通信范围之内。 (4) 择优连接。 若新增加的节点v与局域世界M已存在的节点i进行连接时,其连接概率为 (8) 其中:βi服从(0~1)分布表示超级节点的影响,如果网络中新增节点与网络中存在的超级节点或者超级节点的邻居节点相连,则βi=1,否则βi=0。 (5) 重复步骤(2)~(4),达到要求的网络规模N为止。 (6) 按照1.3节中网络拓扑优化机制实现网络的动态更新。 算法流程如图2所示。 WTOM模型初始化完毕,在网络动态优化的过程中,只有少量超级节点发生微小移动,因此并不影响网络的整体拓扑。无标度网络模型的动态特性可以用连续场理论进行分析论证[13]。考虑到连续性能更详细地刻画所提出模型的性质并预测其度分度,因此,运用连续场理论的方法进行数学论证。模型中任何一个节点的度随时间变化的演化关系,可用连续场近似的方法求得。 当M≥m时,用ki表示节点i的度,并假设ki连续,则在每一个时间步中,节点i的度ki按照式(9)的比率增加。 图2 WTOM模型初始化算法流程图 (9) 式(9)的初始条件为:节点i在ti时刻进入系统,其度数ki(t)=m,且t>0,解微分方程可得 (10) t→+∞时,网络的平均节点度为 (11) 由于时间t服从均匀分布,所以 (12) 由此可得,t→+∞时,节点的度分布趋于 (13) (14) 因为输入超级节点的概率0≤p<0.1,故2 4.1 实验参数设置 运用Matlab仿真工具和Gephi网络构建工具,分析关键参数对WTOM模型的影响,并将WTOM模型与原始的BA模型在模型特点、平均路径长度、聚类系数、能耗和生命周期方面进行对比。表1列出了实验参数表,采用文献[14]的通信模型模拟网络能量的消耗,其中超级节点最大传输半径为普通节点最大传输半径的2倍,节点发射功率可调。 表1 仿真实验参数设置 4.2 WTOM模型和BA模型比较 仿真实验共分为两组,第1组为按照WTOM模型择优概率形成的模型,第2组为按照BA模型生成算法形成的模型,其中p=0.05。图3(a)和图3(b)为两组模型图。表2列出了两组模型相同编号节点对应度的变化。图3(a)中的编号节点为WTOM模型中的超级节点,图3(b)中的编号节点为BA模型与图3(a)中超级节点对应的相同编号节点。 由图3(a)和图3(b)及表2可知,WTOM模型中超级节点比BA模型中对应相同编号的节点连接的边多,即度大。这是因为在WTOM模型中超级节点具有较高的能量,这样有利于网络能量的均衡消耗。 表2 WTOM模型和BA模型相同编号节点对应度的变化 图3 WTOM模型(a)及BA模型(b) (N=100,p=0.05) 4.3 WTOM模型和BA模型度分布比较以及重要参数对WTOM模型度的影响 本文研究了WTOM模型和BA模型度分布的特征以及各关键参数对WTOM模型度分布的影响。图4为p=0.05时WTOM模型和BA模型的实际度分布以及理想的度分布图。p=0时,网络中无超级节点,此时WTOM模型和BA模型完全相同。图5为n取不同值时WTOM模型的度分布图。 从图4可知,WTOM模型和BA模型都具有度大的节点分布概率小、度小的节点分布概率大的特点。WTOM模型中,度在一段范围内出现平坦的状况,但从网络整体度分布看,网络具有无标度性;由于网络中超级节点的存在,其度分布的幂指数变大,度较高的节点数目降低,这有利于降低网络中某些节点因度过大消耗较多的能量,导致过早死亡。从图5可知,适当地增加超级节点的能量也可以降低节点因过度消耗能量导致的失效,从而达到均衡网络能量消耗,增加网络稳定性的效果。 图4 WTOM模型和BA模型度分布 图5 超级节点能量对WTOM模型度分布的影响 4.4 WTOM模型和BA模型平均路径比较以及重要参数对WTOM模型平均路径的影响 图6示出了WTOM模型和BA模型平均路径分布图。图6表明添加超级节点可以有效地降低网络的平均路径,降低信息在网络传递过程中的跳数;增加超级节点的能量对平均路径几乎没有影响。图7示出了超级节点个数对WTOM模型平均路径的影响。图7表明适当增加超级节点个数可以降低网络的平均路径,但达到一定数目时,网络的平均路径几乎不再发生变化。 4.5 WTOM模型和BA模型聚类系数比较以及重要参数对WTOM模型聚类系数的影响 图8示出了WTOM模型和BA模型的聚类特性。图8表明WTOM模型具有较大的聚类特性,大的聚类系数使得局部网络节点间连接具有更高的稳健性,增加超级节点的能量,聚类系数有所增加。图9示出了超级节点个数对 WTOM模型聚类系数的影响。图9表明增加超级节点个数,WTOW模型的聚类系数没有规律地变化。 图6 WTOM模型和BA模型平均路径 图7 超级节点个数对WTOM模型平均路径影响 图8 WTOM模型和BA模型的聚类系数 4.6 WTOM模型和BA模型抗毁鲁棒性比较 为比较WTOM模型(p=0.1)和BA模型的抗毁鲁棒性,表3中统计了WTOM模型(p=0.1)和BA模型最大连通分支上的节点数随周期数r的变化结果。 图9 超级节点个数对 WTOM模型聚类系数的影响 由表3可以看出,在通信过程中,WTOM模型比BA模型具有较好的抗毁鲁棒性。这是因为WSNs节点的失效很大程度上是由能量耗尽引起的,而WTOM模型在拓扑构建的过程中考虑了剩余能量和度的影响,拓扑优化过程中考虑了对关键节点的保护,有利于维持网络的连通性,从而提高了网络的抗毁鲁棒性。 4.7 WTOM模型和BA模型生命周期比较以及能量消耗分析 实验采用SEP路由算法,实验参数见表1。图10(a)示出了存活节点数与周期数的关系;图10(b)示出了能量消耗率与周期数的关系,均在N=100,p=0.1,n=2条件下进行实验。 图10(a)表明BA模型在进行300多个周期时节点开始死亡,而WTOM模型中节点到400多个周期时节点才开始死亡;超过310个周期后WTOM模型比BA模型存活的节点数多;除此之外WTOM模型比BA模型延长了整个网络的生命周期。图10(b)显示BA模型节点能量消耗率高于WTOM模型的能量消耗率,WTOM模型有利于提高能量的利用效率,从而提高网络的生命周期。 表3 最大连通分支上的节点数随周期数的变化 图10 WTOM模型和BA模型中存活节点数和能量消耗率的比较 本文基于BA无标度网络理论,提出了一种拓扑优化模型。通过引入超级节点并结合粒子群算法将网络合理地划分区域;在节点间建立虚拟力场,利用虚拟力调整超级节点目的性的移动,实现网络中关键节点的保护,均衡网络节点的能量消耗。实验结果表明与原始的BA模型相比该模型更具有小世界特性、延长网络生命周期的特点。 [1]YICK J,MUKHERJEE B,GHOSAL D.Wireless sensor network survey[J].Computer Networks,2008,52(12):2292-2330. [2]WANG Bing,TANG Huanwen,GUO Chonghui,etal.Entropy optimization of scale-free networks robustness to random failures [J] .Physica A,2006,363(2):591-596. [3]ZHENNG Gengzhong,LIU Qiumei.Scale-free topology evolution for wireless sensor networks [J].Computers & Electrical Engineering,2013,39(6):1779-1788. [4]TAO Shaohua,YAN Jingfeng.Synchronization enhance on scale-free network[C]// 2011 3rd International Workshop on Intelligent Systems and Applications (ISA).USA:IEEE,2011:1-4. [5]ZHENG G,LIU S,QI X.Scale——Free topology evolution for wireless sensor networks with reconstruction mechanism[J] . Computers & Electrical Engineering,2012,38(3):643 -651. [6]李晓诚.基于小世界模型的无线传感器网络由算法的研究 [D].南京:南京邮电大学,2012. [7]姚洪兴,周飞.基于复杂网络的无线传感器网络在沙漠治理维护中的研究[J] .计算机应用研究,2014,31(10):3033-3036. [8]GUIDONI D L,MINI R A,LOUREIRO A A.Applying the small world concepts in the design of heterogeneous wireless sensor networks[J].IEEE Communications Letters,2012,16(7):953-955. [9]WANG D,LIU E,ZHANG Z,etal.A flow-weighted scale-free topology for wireless sensor networks[J].IEEE Communications Letters,2015,19 (2):235-238. [10]JIAN Y,LIU E,ZHANGN Z,etal.Percolation and scale-free connectivity for wireless sensor networks[J] .IEEE Communications Letters,2015,19(4):625-628. [11]ZHU H,LUO H,PENG H,etal.Complex networks-based energy-efficient evolution model for woreless sensor networks[J].Chaos Solitons & Fractals,2009,41(4):1828-1835. [12]刘军,于耕,张慧鹏.基于节点控制的空间信息网络拓扑重构算法[J].电子学报,2011,39(8):1837-1844. [13]CHEN Hongbin,TSE Chi K,FENG Jiuchao.Impact of topology on performance and energy efficiency in wireless sensor networks for source extraction[J].IEEE Transactions on Parallel and Distributed Systems,2009,20(6):886-897. [14]REN J,ZHANG Y,ZHANG K,etal.Lifetime and energy hole evolution analysis in data-gathering wireless sensor networks[J].IEEE Transactions on Industrial Informatics,2015,12(2):788-800. WSNs Topology Optimization Model Based on BA Scale-Free Network LU Zhi-jing, HUANG Ru, SUN Jun-feng, ZHANG Lei (School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237,China) Due to the limited energy of wireless sensor nodes, the maximization of the network lifetime has become one of the most important problemsin the optimization of the network topology.This paper presents a wireless sensor networks topology optimization model (WTOM) based on BA scale free network. Some super nodes are introduced into the network that is divided reasonably by using particle swarm algorithm. The virtual force field driven by multiple factors is established between nodes and the deployment position of super nodes is adjusted by the virtual force. Thus, the nodes' energy consumption is balanced and the robustness of invulnerability is improved by protecting key nodes. Both the theoretical analysis and experimental results demonstrate that the obtained network model not only keep the characteristics of BA scale free network, but also has the characteristics of small world. Moreover, the proposed model can extend the network life cycle and raise the network energy saving in data collection. WSNs; BA scale free network; topological optimization; super nodes 1006-3080(2017)02-0234-07 10.14135/j.cnki.1006-3080.2017.02.013 2016-06-20 国家自然科学基金(61501187,61365005);教育部基本科研业务基金(WH1315009);国际级大学生创新实践基金(201410251044,201310251052) 路智静(1989-),女,河南濮阳人,硕士生,主要从事物联网研究。E-mail:nicylzj@163.com 黄 如,E-mail:huangrabbit@163.com TP391 A
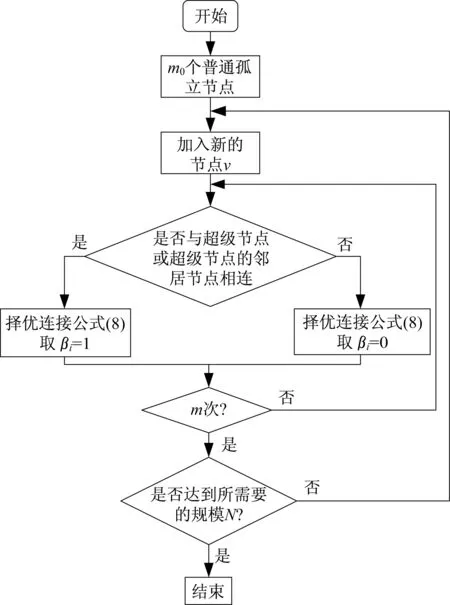
2 WTOM模型的生成机制
3 WTOM演化模型的数学分析
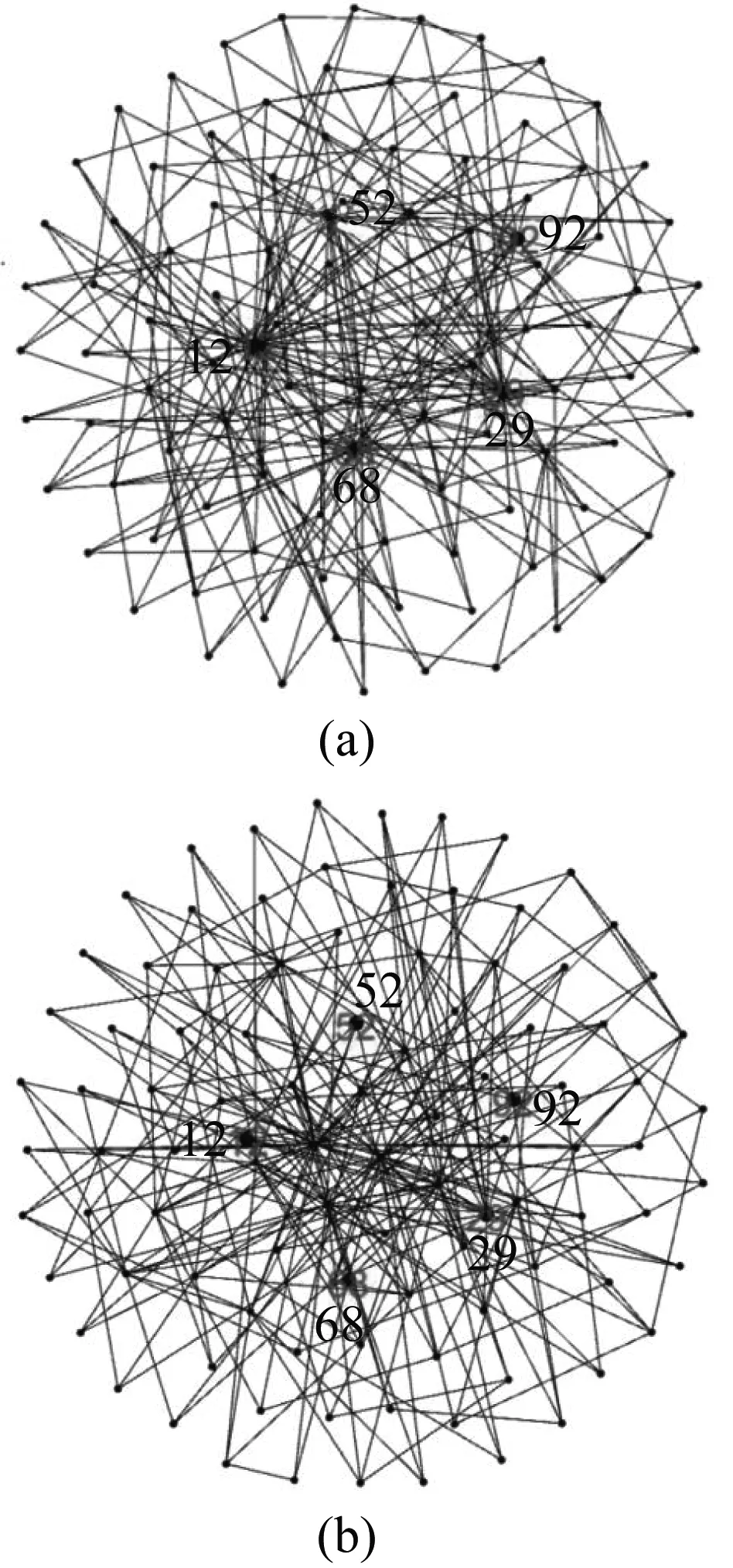
4 实验仿真与结果分析






5 结束语
