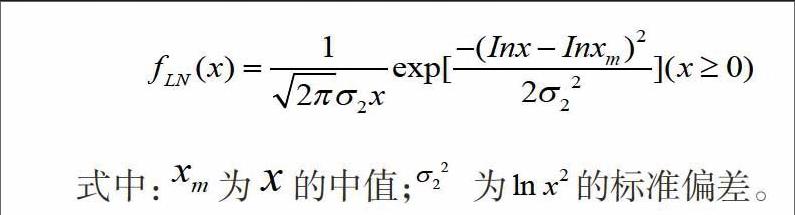海杂波背景下的目标检测算法

潘一舟

摘要：雷达技术一直在民用与军用的各领域扮演着非常重要的角色。在远洋航行的方面，由于海上环境较为复杂，天气等自然因素影响较多，为了保证船只的安全，将雷达技术应用到航行安全保障上面也就顺理成章。

雷达主要通過对目标的检测来判断是否有危险，但正因为各种噪音干扰的存在，雷达的判断不可能始终准确，因而如何减少由于干扰引起的错误判断，对雷达性能的提高就尤为重要。恒虚警率检测是在雷达技术发展过程中提出的一种自适应检测方法，其在复杂的海洋环境下有着较为良好的检测性能，本文主要讨论的就是海杂波环境下的恒虚警率检测。

该文主要讨论海杂波的幅度特征，首先介绍几种主要的杂波幅度分布模型，再介绍几种主要的恒虚警率检测的方法，并对他们的性能进行比较。最后，针对其中的单元平均恒虚警率检测（cA-CFAR），本文给出了其检测流程和门限计算的方法，并用MATLAB进行算法仿真。

关键词：海杂波；目标检测；CA-CFAR；MATLAB

中图分类号：TP391 文献标识码：A 文章编号：1009-3044（2016）29-0225-05

1海杂波分析

1.1海杂波幅度分布模型

海杂波的产生依赖于许多复杂的因素，主要是两大方面的因素：雷达的工作状态以及检测时的海洋环境，具体包括：雷达信号的入射角、发射频率、海面海风的风速和风向等。

由于海杂波的复杂性，我们可以将其视为一种随机过程，然而想要完整地描述一个随机过程是相当困难的，因此在实际中我们只考虑其主要的几个特征，将其视为一个多参数的函数，这些参数有着较强的相关性。本文主要考虑海杂波的幅度分布特征，因为幅度特性是雷达杂波和海杂波共同的主要统计特性之一，对于雷达仿真、目标检测的性能有着十分重要的意义。

海杂波的幅度特征一般是比较均匀的，其主要得分布模型有瑞利分布（Rayleigh）分布、对数-正态分布（Log-normal）、韦布尔分布（Weibull）和K分布等。

1.1.1瑞利分布杂波模型

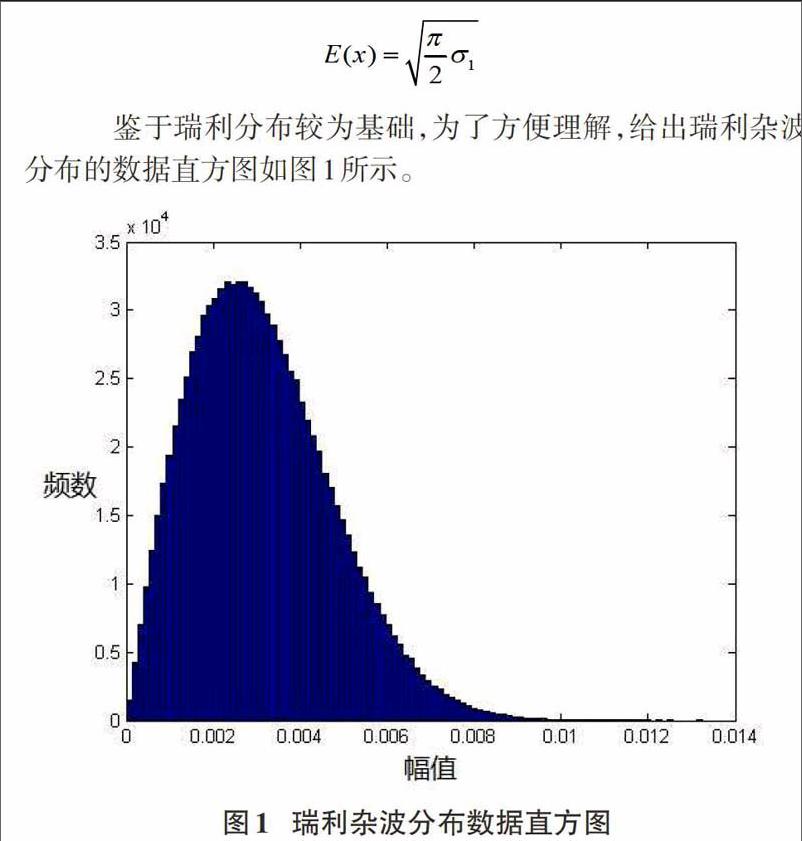
瑞利分布是一种基础分布，一般适用于较低分辨率的雷达杂波幅度模型。其概率密度公式为：

鉴于瑞利分布较为基础，为了方便理解，给出瑞利杂波分布的数据直方图如图1所示。

1.1.2瑞利分布杂波模型的性能讨论

之前提到瑞利分布是一种基础分布，是最早被广大学者研究的幅度模型之一，适用场合为低鉴别清晰度雷达大俯视角时平稳环境的海杂波。使用该模型的基本条件如下：

1）雷达各照射单元内的散射体之间是相互统计独立的；

2）所有散射体中没有一个孤立的散射体能够起到决定性作用；

3）散射体树木足够大，以便满足中心极限定理的条件，使整个信号服从正态分布；

4）照射单元内两散射体雷达距离之差比照射单元的尺度小很多，且在单元内天线的增益是常数。

瑞利分布作为一种基础分布，对雷达波束的入射角度要求较高，对于大振幅出现概率较高的情况，检测性能也不是很好，现如今已经很难满足现代雷达清晰度的要求了，但是其还是存在一定的研究意义。

总结一下关于瑞利分布，适用于相对独立、随机零散的小散射群体，以及低分辨率低海情时的雷达检测。

1.1.3对数-正态分布杂波模型

对数t态分布是一种针对瑞利分布改进后的杂波分布模型，适用于多种海浪，其概率密度公式如下：

1.1.4对数-正态分布杂波模型的性能讨论

针对大振幅出现概率增加时瑞利分布拟合不够好的情况，可以使用对数-正态分布来替代瑞利分布，但是由此带来的问题就是，其动态范围要远远宽于瑞利分布，容易出现动态范围过于宽广的情况。

综合来看，对数-正态分布适用的场合为高分辨率和较高海情时的雷达检测，因为此时对数-正态分布可以有效解决海杂波的后向散射特性。

1.1.5 K分布杂波模型

K分布是较晚提出的一种分布模型，但是在实际中却受到了专家学者们越来越多的重视。在该模型中，将海杂波的幅度分为了两个部分，一个部分是慢变化分量也称均值分量，该分量是一个调制分量，随时间变化较慢，数量级为秒，反映了大的海涌、重力波等的运动特性。另一个部分是快变化分量，也称为斑点分量，其随时间变化较快，在毫秒数量级上，符合瑞利分布，反映了海表面毛细波等微小破碎的运功特征。因而，K分布作为一种混合模型，从整体和细节上都能有很好的拟合表现。尤其是在幅度分布上能很好地表现低擦地角、高分辨率雷达杂波的长拖尾特性。同时，之前提到的瑞利分布等，也均是特殊情况下的K分布，可以很好地整合到该模型中。

K分布的概率密度函数为：

式中：v是形状参数，α是尺度参数，г（.）是伽马函数，K_v（0）是第二类修正贝塞尔函数（x>0，v>0）。其中α反映了回波的功率特性，其值越大，回波功率越强；形状参数v反映了海杂波的尖锐程度和K分布的偏斜度（其取值范围一般为02，v和α之间的关系可以表示为：

2雷达杂波的恒虚警率处理

雷达的目标检测是对于一个物体存在与否进行判断，通常的办法是设定一个门限值（固定门限），每当信号超过该固定门限值时就判定为目标存在，反之若没有超过该固定门限的就判定为目标不存在，或者说该信号为干扰或噪声信号。而虚警的概念就是在这种判定模式下，如若信号本身在噪声的干扰下，使得原本不应该超过判决门限的却超过了判决门限，造成实际情况中应该判定为不存在的目标被判定为存在的情况。对应于海杂波背景下的目标检测，就是在背景噪声的干扰下，造成没有目标点的回波信号过了判决门限，使得雷达误判定此处有目标。

需要指出的是，除了上述提到的虚警。还有一类情况称之为漏警，即目标信号回波很小或者目标距离雷达较远，回波幅值没有超过门限，那么就会被认为是杂波或者噪声，判决为没有目标的存在从而产生了漏警现象。在雷达的目标检测中，虚警与漏警都是我们不想看到的情况，我们把规定检测时间内出现虚警的概率称为虚警率，出现漏警的概率称为漏警率，不难看出，虚警率与漏警率是判断雷达性能优良的重要指标。

由此可见，固定门限的检测方法存在很大的缺陷，对许多复杂情况的适用性不高且容易造成虚警与漏警情况的发生，所以，自适应门限检测技术的产生与运用也就显得顺理成章了。顾名思义，自适应门限检测技术就是当杂波背景环境或者噪声干扰发生变化时，检测门限也随之改变的检测方法，通过改变检测门限，使得虚警率保持恒定。

2.1雷达的恒虚警率检测

雷达的恒虚警率处理（Constant False Alarm Rate）简称为CFAR，其基本原理如下：

分别用P_fa和P_d表示虚警概率与检测概率（正确检测出有目标的概率）。

如果用v（t）表示雷达回波信号，则v（t）=s（t）+n（t），其中s（t）表示目标信号，n（t）表示噪声。显然：s（t）=0时表示目标不存在，s（f）=1时表示目标存在，同时这也是雷达信号空间的一个完整划分。

虚警概率可以表示为：

P_fa=P_t[判决s（t）存在|s（t）不存在]

正确检测概率可以表示为

P_d=P_t[判决s（t）存在|s（t）存在]

漏警带来的损失我们用L₁表示，虚警带来的损失我们用L₀表示，因此，平均损失函数L可以表示为：

L=qP_faL₀+p（1-P_d）L₁

式中p和q分别是信号存在与否的先验概率。

2.2最佳检测

最佳检测是从有噪声和干扰的信号中提取有效信息的最佳方法，最佳检测通常采用的是二元检测和最大似然比准则。有概率论基本知识可知：

若H₁表示目标信号存在，H₀表示目标信号不存在，我们可以得到公式：

2.3虚警的控制

固定门限的缺陷是海情大幅變化时，虚警率会大幅上升导致检测性能急剧下降。因而，需要恒虚警处理以保证检测性能。

要想做到保持虚警率的恒定，必然需要能够自动形成与噪声和干扰环境相匹配的自动检测门限值。根据之前提到的漏警和虚警的概念，我们可以推测出自适应门限电平不是单纯地越小（大）越好。门限电平越低，检测到目标的概率越大，但这其中包含虚假目标的可能性也越大，即虚警率越高；相反地，门限电平越高，虚警率确实会降低很多，但是检测到目标的概率也随之下降，许多小目标弱信号检测不到，造成漏警。无论哪种情况，都不是我们想要看到的，也都不利于雷达性能的提高。

因此，虚警的概率不是说越低越好，而是需要采取一个折中的方案，在系统可允许的虚警范围内，使得检测到目标的概率越高越好。

2.4雷达信号恒虚警率处理的几种方法

下面介绍几种常见的恒虚警率处理方法：

2.4.1基于单元平均的CFAR（CA-CFAR）

基于单元的平均恒虚警率处理是研究时间最早，理论体系最为完备的一套恒虚警率处理方法，其基本原理是通过将待检测目标周围邻近单元作为参考单元，通过加权平均的方式计算出自适应检测门限电平，以此作为判断目标是否存在的依据。然而参考单元并不是越多得到的结果就越好，道理很容易理解，假设现在取得邻近单元非常多，那么意味着在边缘的邻近单元与目标单元距离就非常之远，从而不再可以算作是“邻近”单元，相关性也很弱，即基本上对于目标单元的检测毫无贡献。因而参照单元的选取也必须在一定范围内。

CA-CFAR中的信杂比SCR（signal clutter rate）定义如下：式中a为目标信号回波幅值，c为杂波回波幅值，K为杂波统计数据总个数。信杂比为衡量雷达性能的一个重要指标。

CA-CFAR在均匀杂波背景下的检测性能较为良好，但是如果遇到杂波边缘或者是多目标环境下的检测时，其性能会大幅下降。

2.4.2选大CFAR（GO-CFAR）和选小CFAR（SO-CFAR）的恒虚警率处理

之前提到CA-CFAR在杂波边缘或者是多目标边缘下检测性能会大幅下降，为此，学界提出了选大CFAR以及选小CFAR来弥补对应情况下CA-CFAR的不足。顾名思义，选大和选小CFAR分别是对检测目标两侧的参考单元分别作算术平均，然后分别是在两个结果中选择大的和选择小的作为处理结果。可以看出，选大的处理方法可以有助于处理杂波边缘而选小的方法有助于多目标环境下的检测。

2.4.3统计排序CFAR（OS-CFAR）的恒虚警率处理

不同于上述几种简单的做算术或者加权平均的处理，统计排序CFAR在将邻近单元进行升序排序后，再按照某种标准选取第K个值，处理后与门限值T相乘后送入比较器，与检测单元进行比较，再得到信号输出。统计排序CFAR，可以在大小目标相邻时，在一定虚警率下，避免大目标信号遮盖小目标信号的情况，将小信号也检测出来，某种程度上显著提高了雷达的检测性能。

3CA-CFAR检测器的实现

3.1单元平均CFAR（CA-CFAR）检测流程

鉴于上一章已经对CA-CFAR做了初步说明，这里只补充一些必要的细节。需要指出的是这里只讨论了幅值特性，因而都以复数数据的模值进行计算。CA-CFAR的检测原理框图如图2所示。

4结束语

本文只是针对瑞利杂波分布下，较为基础的CA-CFAR恒虚警检测做了重点介绍，且仅限于幅值特征。近年来，随着广大学者不断深入研究，提出了包括多速率恒虚警检测，双门限恒虚警率检测、多脉冲相干COA-CFAR检测、单元中值CM-CFAR检测器等，可以预见在将来会有更多优秀的自适应检测算法出现。在本文的后续研究中，可以加入相位等因素，考虑除幅度以外的特征，更加贴合实际情况。