一种有效的雷达信号快速识别方法*
2017-04-26何梓昂
杨 建,周 涛,何梓昂
(电子信息控制重点实验室,成都 610036)
一种有效的雷达信号快速识别方法*
杨 建*,周 涛,何梓昂
(电子信息控制重点实验室,成都 610036)
针对多种调制类型的雷达信号快速侦察识别成功率较低的问题,提出了基于瞬时频率特征提取的雷达信号快速识别新算法。首先,由短时傅里叶变换(STFT)得到信号每一部分的瞬时频率特征;其次,对得到的瞬时频率进行两次归一化分别得到各自特征值;最后,用层次决策方法对雷达信号进行分类识别。仿真实验结果证明该方法能有效识别各种雷达信号,在信噪比高于-3 dB时,各种脉内调制的识别成功率都达到90%以上。
雷达信号识别;瞬时频率;特征提取;短时傅里叶变换;脉内调制
1 引 言
雷达信号脉内调制分析及识别方法是当前电子战中电子侦察的重要内容。雷达技术的不断进步使得当前电子侦察所要面对的雷达信号日益复杂,目前成熟的信号分选识别方法是基于脉冲描述字,但对于复杂调制的雷达信号,当前的识别算法实时性差且识别成功率并不高。因此,需要能更快速准确地识别信号脉内调制类型的新方法。
文献[1]通过提取瞬时频率两级归一化特征来识别信号脉内调制,信噪比高于6 dB时,识别6种常用调制信号的正确率可达到90%以上;缺点是信噪比要求比较苛刻,且通过仿真实验发现其算法中某些门限设置并不合理,对于常规脉冲信号和二相编码等信号的识别成功率并不高。文献[2]中提出基于瞬时频率的脉内调制特征识别技术,对于4种信号识别非常有效,但其在低信噪比下识别成功率低,且能识别信号类型很少,需要进一步优化改进。文献[3]中的方法在信噪比高于6 dB时,识别6种常用调制信号的正确率可达到90%以上,但其识别方法仅限于各种调制信号的载频、脉宽、起始频率等调制参数相同的情况,对于参数随机变化的情况不能正确进行分类。文献[4]中提出用图像处理方法来进行信号识别,识别效果较好;缺点是算法计算量很大,工程应用困难。文献[5]通过相位差分来提取信号的时频特征,在信噪比较高时可以识别各种典型的脉内调制信号;缺点是这种方法得到的频率误差较大,且信噪比要求较高。文献[6]直接从得到的瞬时频率的时频分布图来估计各种调制的参数,估计误差较小;缺陷是没有进行信号的识别,直接进行相关调制参数估计。文献[7]则综述了盲信号分类和识别的发展趋势,对研究有指引作用,但未做深入研究。
本文提出基于短时傅里叶变换(Short Time Fourier Transform,STFT)的瞬时频率(Instantaneous Frequency,IF)提取,以及基于二级频率归一化的识别典型雷达信号的方法。由于可通过算法成熟且容易在FPGA和DSP等硬件实现的快速傅里叶变换(Fast Fourier Transform,FFT)来实现STFT,因此,在数据量一定的情况下,该方法可以提高瞬时频率的运算速度,保证了识别信号脉内调制的实时性,且全频段信噪比(Signal-to-Noise Ratio,SNR)(信噪比按整个频段内信号和噪声能量的比值计算)在-3 dB以上识别正确率在90%以上,因此工程应用价值很高。
2 雷达信号瞬时频率和相位的提取
IF的提取基于STFT,其定义式为

(1)
式中:s(t)为信号,h(t)为窗函数,*代表复数共轭。
瞬时频率和相位的提取原理是将信号序列分段,得到很短的时间序列,求得信号的第i段序列的相位和频率为

(2)
f(i)=(k+δ(i))*fs/N。
(3)
式中:max(STFT(t,f)i)为第i段序列FFT后幅值最大的频谱。式(3)中k为幅值最大谱线对应的序号;fs为采样频率;N为FFT点数;δ(i)为频率修正因子,其具体计算方法可参见文献[8]。
整合每一段信号的频率和相位,即可得到瞬时频率和瞬时相位。这种基于STFT的算法,时间窗长越小瞬时性越好,但瞬时频率和相位估计误差越大;窗长越大瞬时频率和相位估计越准确,但瞬时性越差。算法的这一特性决定了在使用时需要平衡瞬时性和准确度的要求,并且在处理窄脉冲时会带来性能的损失。因此需要结合实际系统需求,综合考虑来确定最佳的时间窗长度。
3 常用雷达信号瞬时频率和相位特征
本文中处理的7种典型雷达信号设置如下:
(1)CP信号:载频fc=250 MHz,脉宽τ=10 μs。
(2)BPSK信号:载频fc=250 MHz,脉宽τ=7 μs,编码采用7位巴克码。
(3)QPSK信号:载频fc=250 MHz,脉宽τ=16 μs,编码采用16位弗兰克码。
(4)BFSK信号:两频率f1=130 MHz,f2=460 MHz,脉宽13 μs,编码采用13位巴克码。
(5)QFSK信号:4个频率分别为f1=120 MHz、f2=230 MHz、f3=310 MHz、f4=430 MHz,脉宽τ=16 μs,编码采用16位弗兰克码。
(6)LFM信号:起始频率fo=250 MHz,带宽B=200 MHz,脉宽τ=10 μs。
(7)SFM信号:起始频率fo=250 MHz,带宽B=200 MHz,脉宽τ=10 μs。
将上述各种调制信号经上一节所述的瞬时频率提取后,可以得到在SNR=10 dB时各信号频率与时间的关系如图1~7所示。

图1 CP信号的瞬时频率
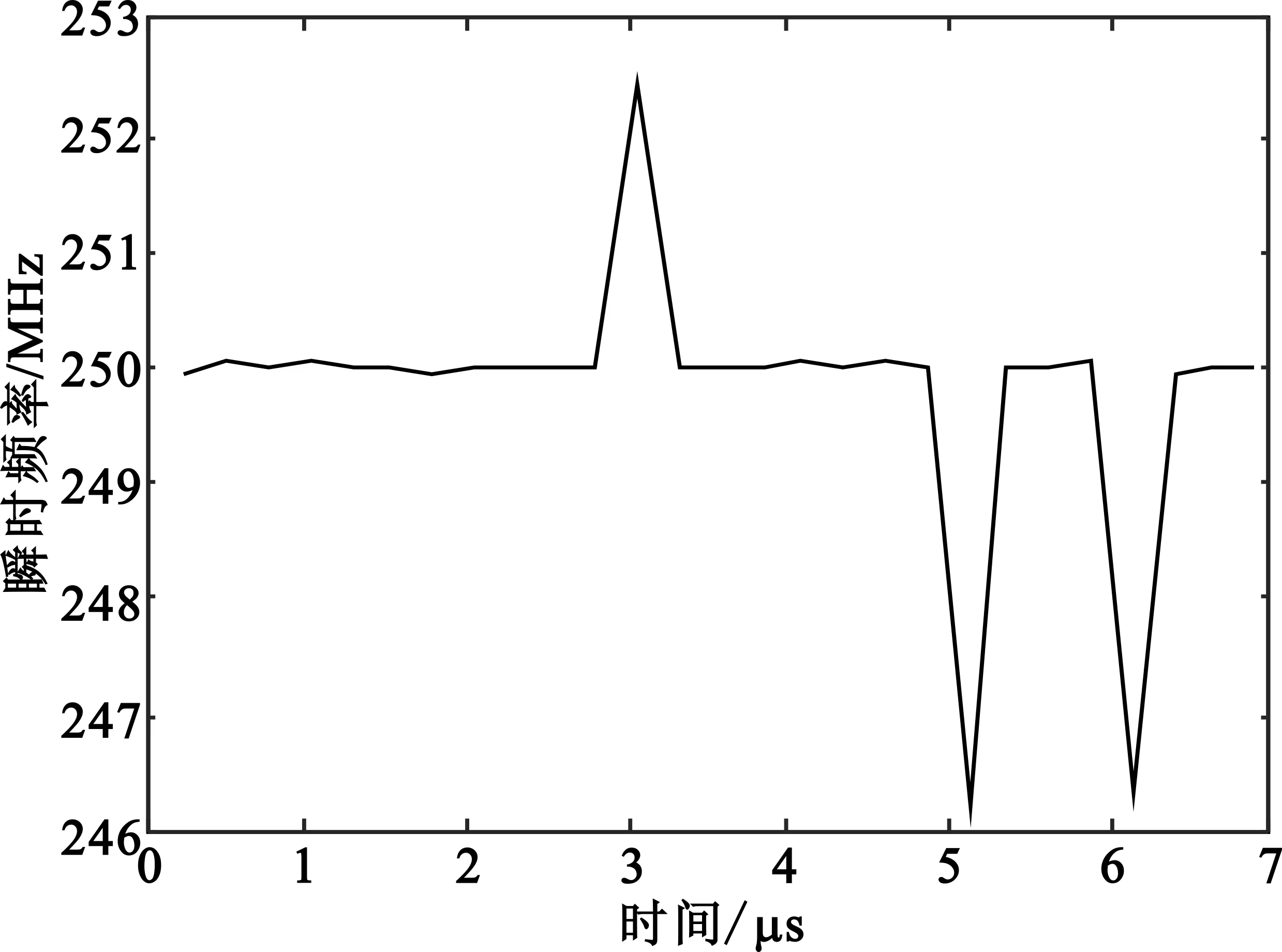
图2 BPSK信号的瞬时频率

图3 QPSK信号的瞬时频率

图4 BFSK信号的瞬时频率
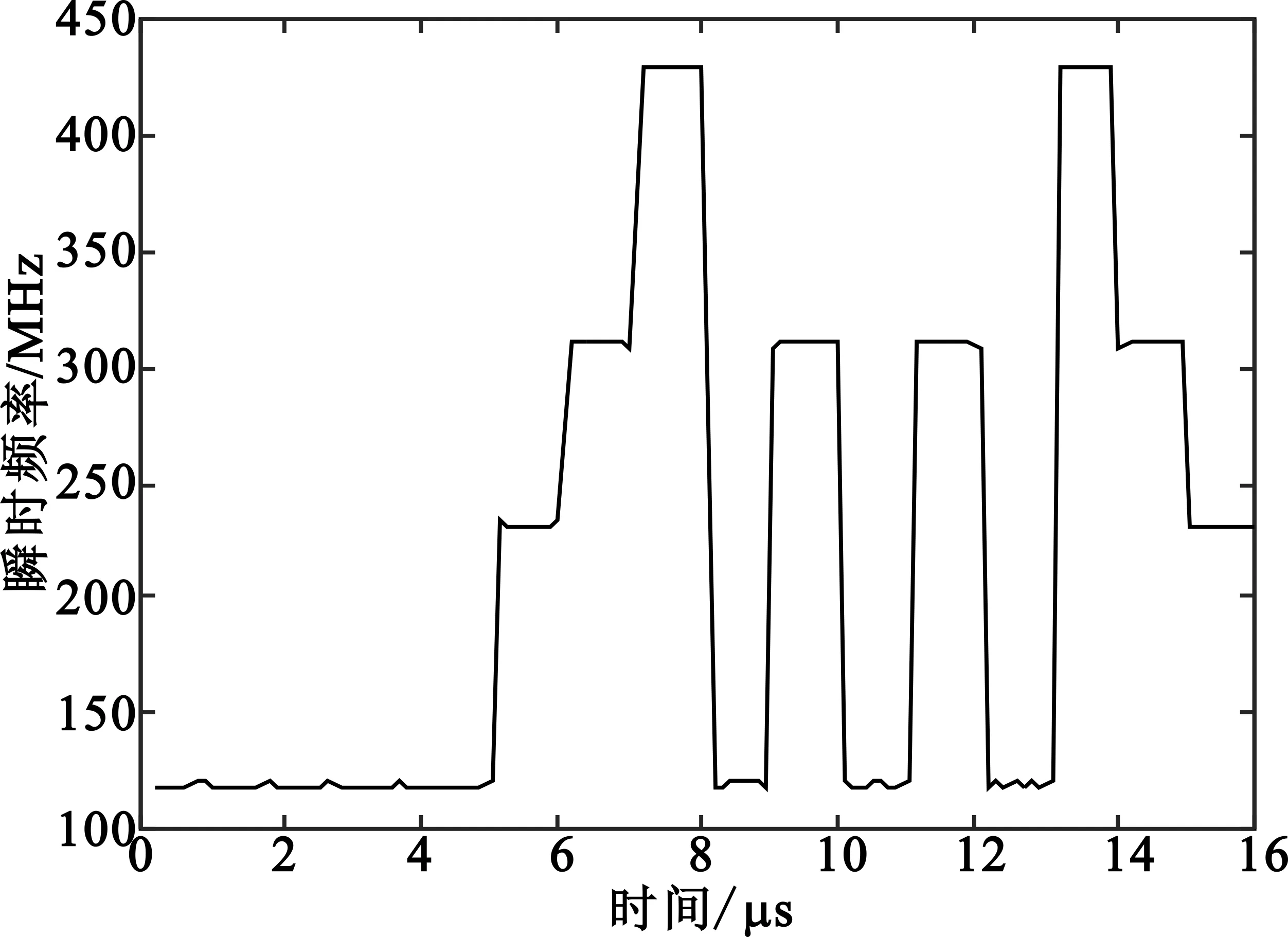
图5 QFSK信号的瞬时频率
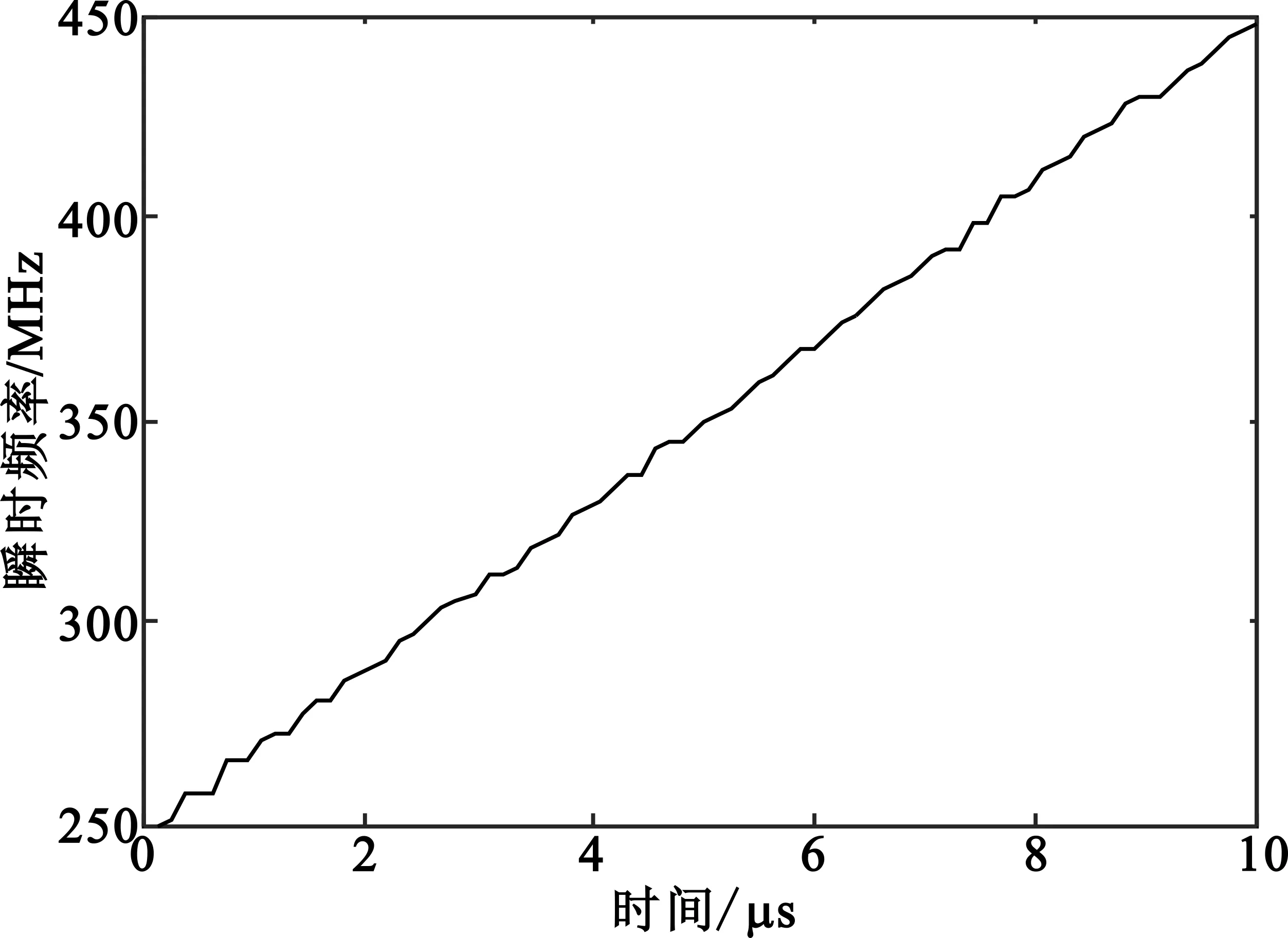
图6 LFM信号的瞬时频率

图7 SFM信号的瞬时频率
各调制信号分别有各自的IF特征,得到这些时频关系图后人工进行判断和识别非常简单。但实际应用中人工判断信号调制类型效率非常低,且接收机处理的数据量巨大,更需要根据接收的脉冲快速判断调制方式。因此,本文提出一种瞬时频率归一化后提取特征来识别信号调制类型的方法,该方法适用于计算机快速准确判断接收信号脉内调制类型。
4 雷达信号的识别
由图1~7可以发现不同信号IF的分布中心(均值)和相对该中心的偏离程度一般情况下各不相同[3]。归一化后的IF能体现脉内调制特征,有些信号一次归一化后仍然无法识别调制类型,需要进行二次归一化进一步提取特征量进行识别。
4.1 瞬时频率归一化处理方法
归一化之前首先要考虑一种影响识别结果的情况:噪声和测频方法的影响使相位编码信号的IF极值小于其均值(倒峰),例如图2中BPSK信号的IF后半部分极值小于整个IF的均值。由于后面分析中默认IF跳变极值大于其均值(正峰),因此通过式(4)对IF进行翻转,以处理后的序列进行两级归一化。
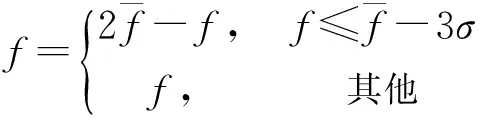
(4)
式中:σ为f的方差。然后,通过式(5)对瞬时频率序列f进行归一化:
f1=f/fm。
(5)
式中:fm为f序列的最大值。得到归一化IF序列f1其范围为[0,1],并可得其均值E1和标准差σ1。
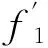
4.2 信号识别方法
首先,识别特征最明显的BFSK信号;其次,分析最简单的CP信号;然后,是BPSK、QPSK信号;最后,对LFM、SFM和QFSK信号进行识别分类。
4.2.1 BFSK与QFSK信号识别
BFSK信号两次归一化后特征最明显,由于第二次归一化后其频率序列f2仅提取了f1序列中频率较高的部分,因此f2的所有值都接近于1,取值集中所以σ2非常小。而第一次归一化后由于有两频率取值更分散所以σ1较大,因此BFSK信号的σ1>σ2。而QFSK信号由于有4个频率值,因此其σ1大于和小于σ2都有可能。
D1=σ1-σ2,
(6)
若D1>0则可判断为FSK信号。由于BFSK极值只有一种,而最简单的QFSK信号极值至少有4种,为区分BFSK和D1>0的QFSK信号,可将极值个数NF作为区分两者的特征量。
应用直方图法求FSK信号NF,即将频率差分值划分至相应区间内,如图8为QFSK信号一级归一化频率差值的分布情况,图中共有4种跳变值。
4.2.2 CP与BPSK及QPSK信号识别
由图1和理论分析可知,常规脉冲信号的IF在所有信号中最平坦,其第一级归一化频率序列f1所有值都非常接近1。由于噪声干扰使其IF序列产生一些极值,导致CP瞬时频率序列与相位编码信号类似,两者归一化后均值E1都接近1。而其他信号则要小很多,实验表明CP和PSK信号的E1在0.9以上,这一特征可作为识别CP和PSK类信号的特征量。
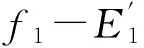
D2=E1-E2。
(7)
综上所述,可由E1≥0.9且D2≥0.45判断信号为PSK或CP信号,然后通过E2值区分CP和PSK信号。但是由于噪声及测频误差影响,会导致两类信号E2值可能在0.2附近交叉,利用相位差峰值数NP可进一步提高分类准确度。通常CP信号IF峰值数为0,信噪比很低时可能有1~2个,而对于7位巴克码调相的PSK类信号的峰值数一般大于3个,所以用E2和NP值即可区分两类信号。
为准确得到信号的NP值,考虑设置自适应门限:利用CP信号的相位差序列最大和最小值的差一般远小于PSK这一特点,当此差值小于2.5 rad时,初步认为是对CP信号求峰值,因此设置门限为Ep±3σp,其中EP为相位均值,σP为相位的方差。当最大值最小值差大于2.5 rad时,则认为是对PSK信号求峰值,设置门限为Ep±σp。
设置自适应门限效果如图9所示:门限1的值是Ep±σp,门限2是Ep±3σp,图9(a)中最大值最小值差大于2.5 rad,门限值设为Ep±σp,对于7位巴克码调相的BPSK信号,3个峰值都超过该门限;图9(b)中最大值最小值差小于2.5 rad,设置门限值为Ep±3σp,对于CP信号没有超过该门限的峰值。因此,自适应门限法能得到信号真实峰值数。
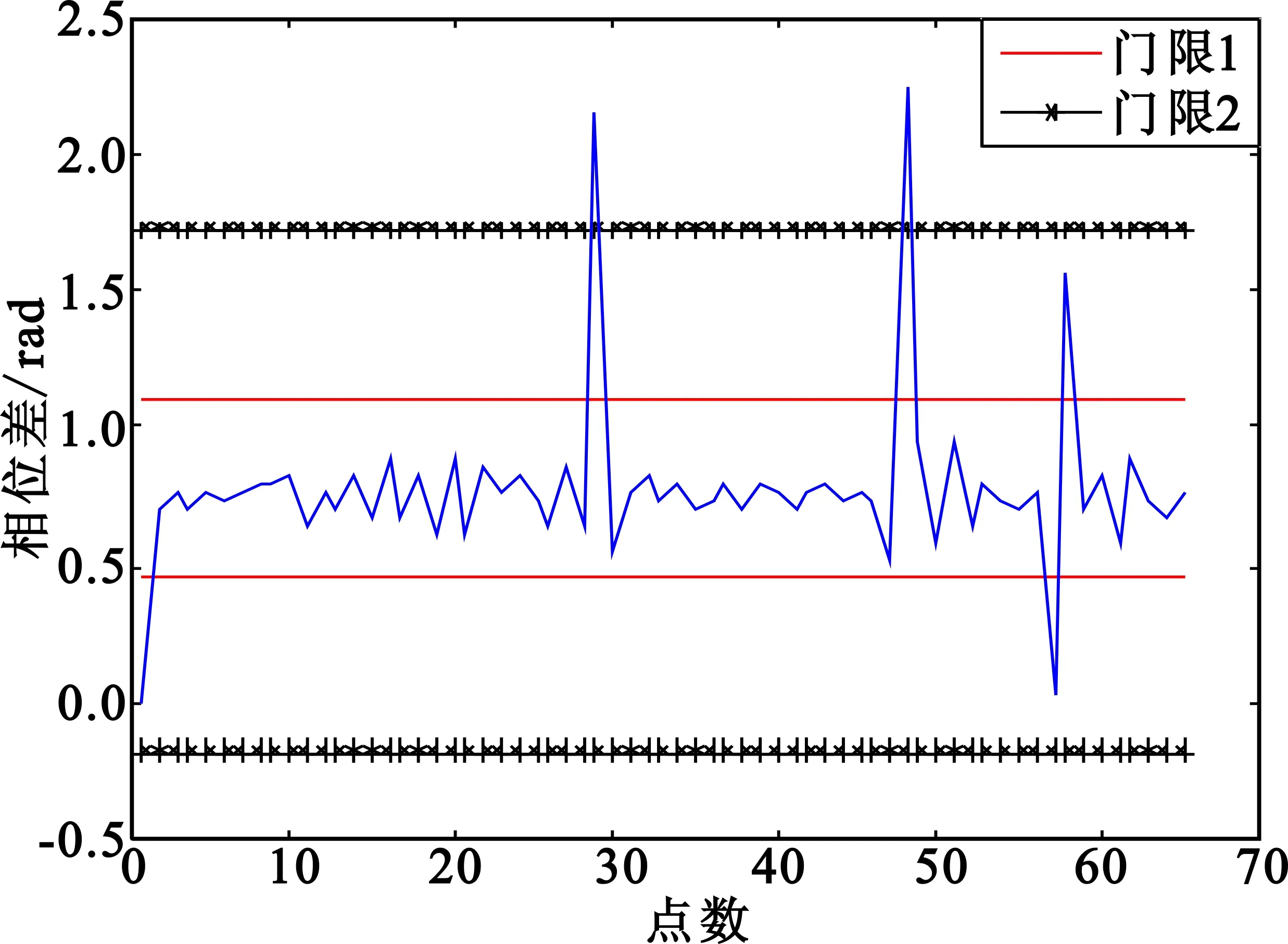
(a) BPSK信号相位
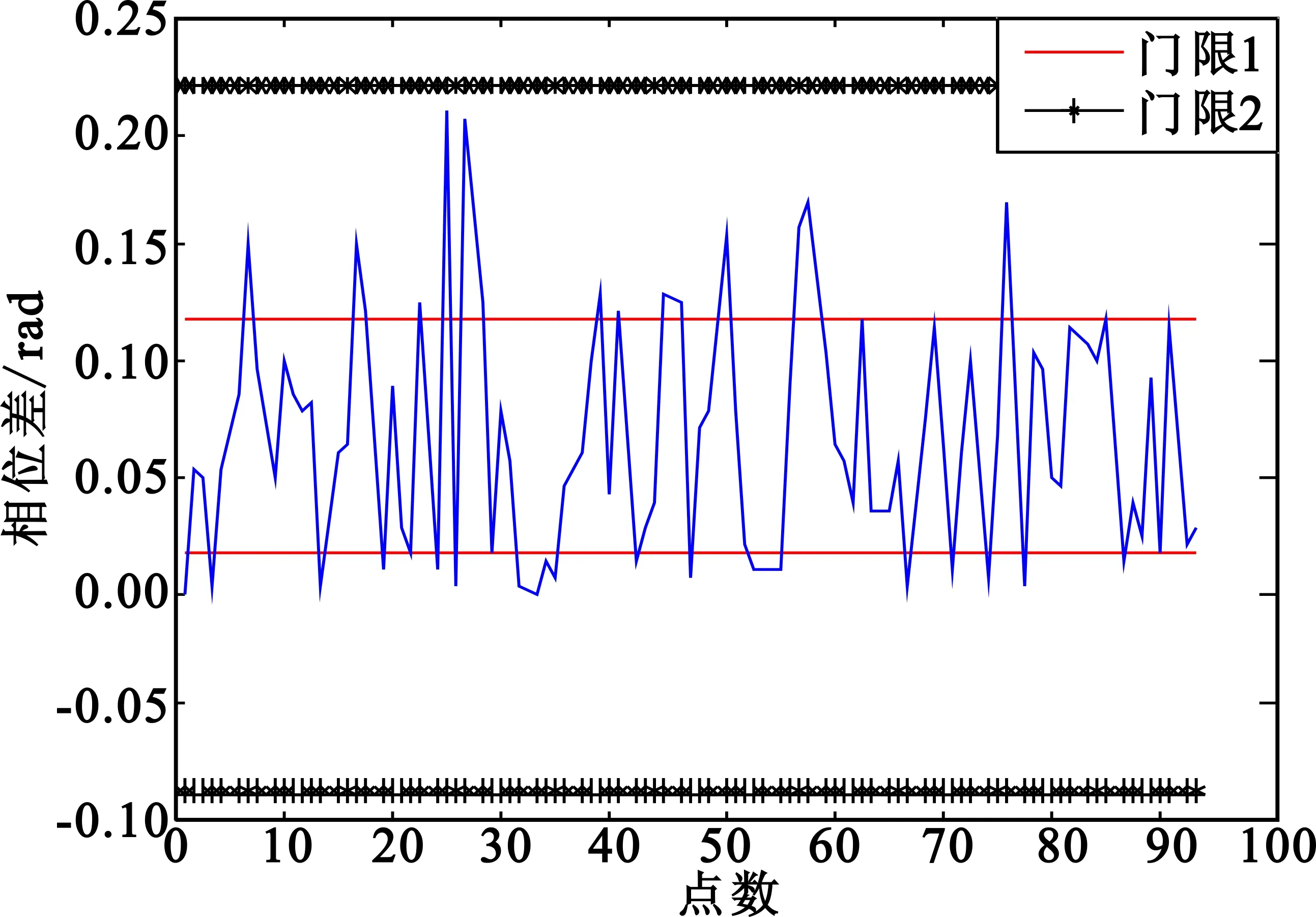
(b) CP信号相位差
4.2.3 LFM与SFM及QFSK信号识别
LFM信号的频率线性变化,SFM信号频率按正弦规律变化,两信号频率变化平缓没有跳变,它们的NF基本为0。而QFSK信号有4种不同的频率值,频率跳变值至少有3种。因此,NF≥3 时即可判为QFSK信号。
通过分析可以发现,LFM和SFM信号两次归一化频率均值的差D2=E1-E2取值在0~0.45,可以通过D2<0.45来识别LFM和SFM信号。对于理想的LFM信号的频率满足中心对称性即式(8):
fmid=(forigin+fend)/2 。
(8)
式中:fmid为f1序列中点值,forigin是频率f1序列起点值,fend是频率f1序列终点值。可以由式(9)、(10)构造新的特征量Fd1和Fd2:
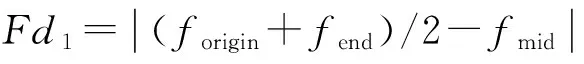
(9)

(10)

5 仿真实验及分析
5.1 确定信号分类识别流程及门限值
用Matlab对本文算法进行仿真,应用蒙特卡洛方法保证仿真结果的可靠性。采样率fs=1 GHz,STFT窗长128点。SNR范围-10~20 dB,间隔为1 dB。每一SNR下进行200次蒙特卡洛实验。实验对象为中频信号,故信号参数设置同第3小节。
对上一节中识别信号用到的各个特征量,在SNR取0~20 dB时(SNR低于0 dB时没有参考价值),通过200次蒙特卡洛实验得到的取值范围结果如表1所示。
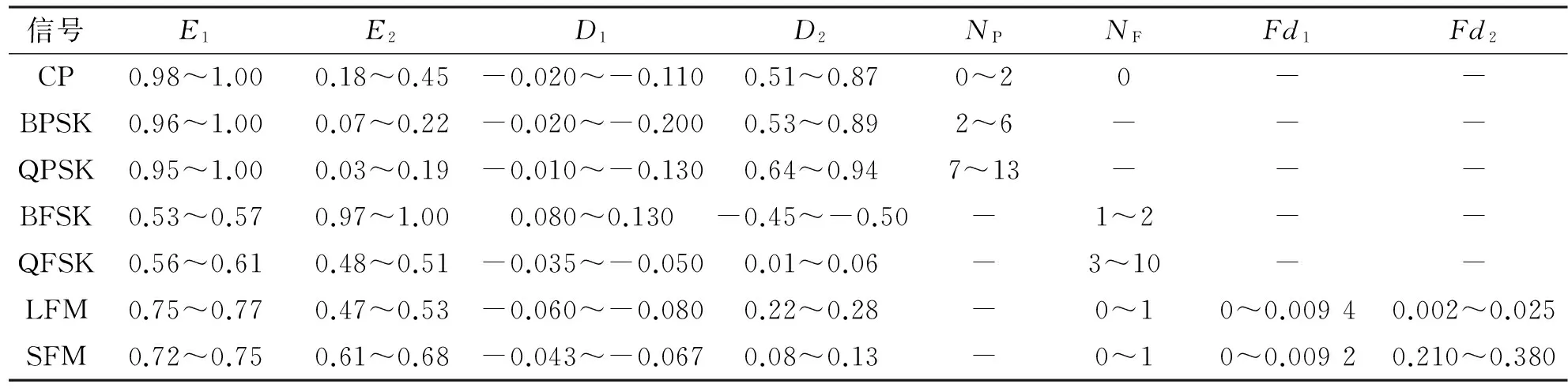
表1 各信号特征量的取值范围(0~20 dB)
由表1可知,D1是效果非常好的分类特征量。在所有信号中只有FSK类信号的D1大于0,其他信号的D1都小于0,与上一节中的分析结论相同。所以D1的门限就定为0,可以最先识别出FSK类信号。由NF区分BFSK和QFSK,门限设为3。
CP信号和PSK类信号E1≥0.9且D2≥0.45,特征明显可作为第二个识别判断条件,而CP信号和PSK信号的E2以0.2为门限,区分BPSK和CP的NP门限设置为2,而区分BPSK和QPSK时NP门限值设置为6。
剩余几种信号中NF作为识别QFSK信号的特征量其门限设为3。
最后对于调频类信号其D2都小于0.45,因此其门限设为0.45。对于LFM和SFM分类所用到的Fd1和Fd2其门限取值为0.029 5。
综合上一节分析完成了对7种信号的识别分析,分类特征越明显的特征量应首先用于分类判别,其位置越靠前。信号的识别流程如图10所示。
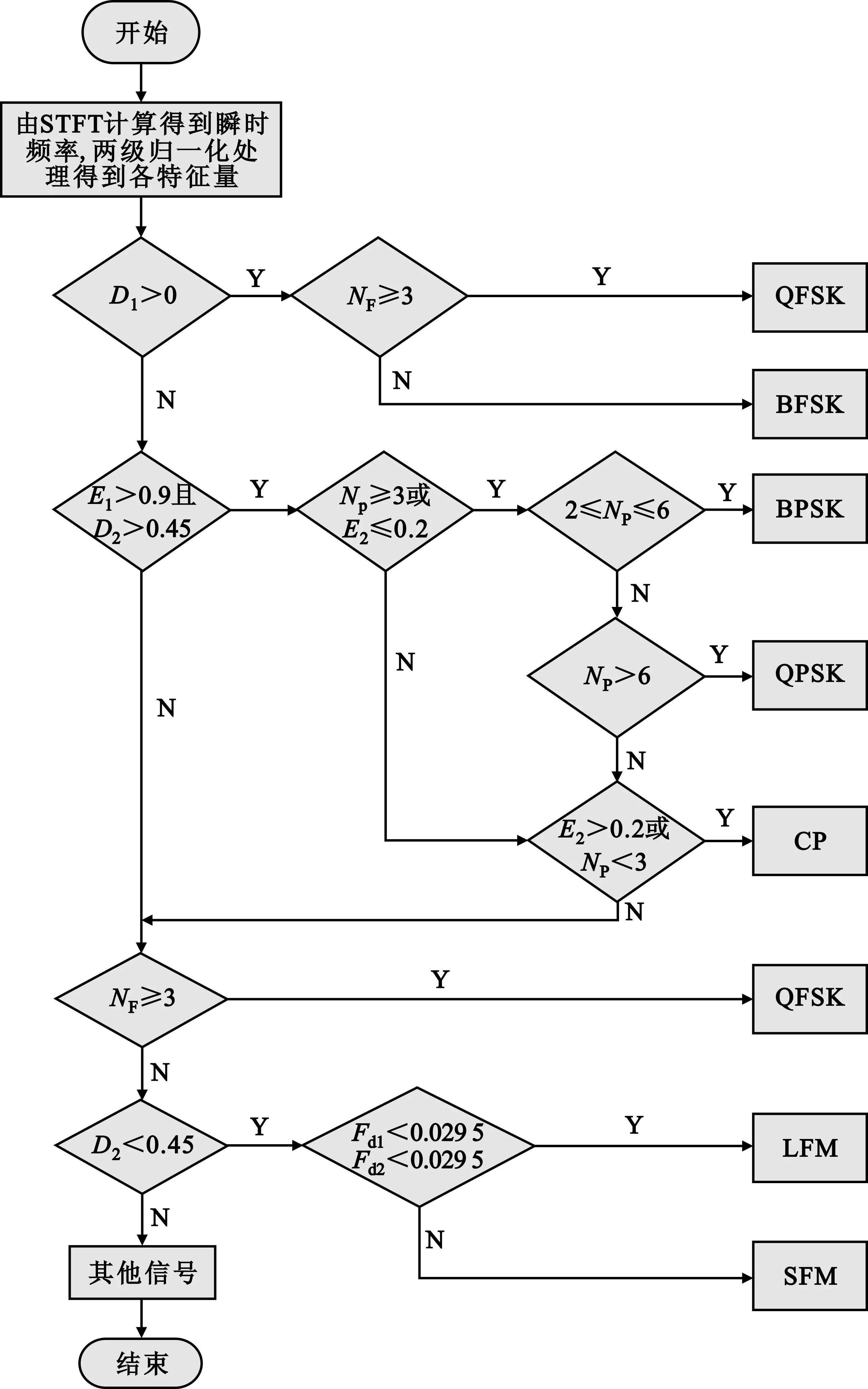
图10 层次决策信号分类流程
5.2 实验结果分析
各类信号脉宽取值在7~16 μs时,图11给出了SNR从-10~20 dB每隔1 dB信号识别成功率随SNR变化的曲线。
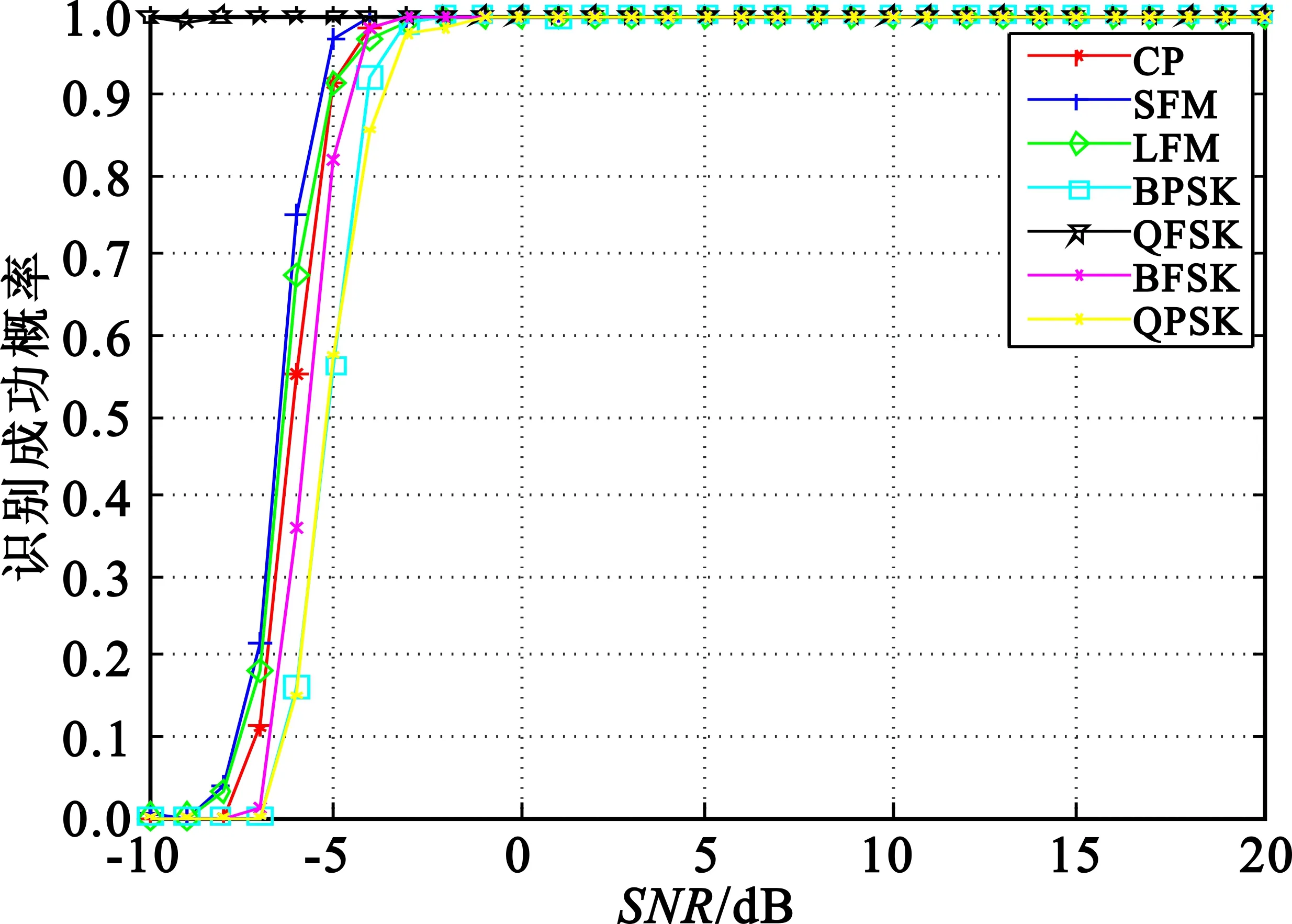
图11 各类信号识别成功率
由各信号的识别成率曲线可知,当SNR≥-3 dB时,7种信号识别成功率都在90%以上。当SNR≥0 dB时,识别成功率都在98%以上,识别效果较好,且识别信号调制类型的实时性好,这都体现了算法性能的优越。当SNR≤-5 dB时,识别成功率急剧降低,当SNR≤-7 dB时识别成功率几乎为0。原因是SNR低于-7 dB时,信号提取的各个特征量值受到噪声影响,不再能够体现出调制规律。
5.3 与经典识别算法对比
文献[1]和文献[2]是经典的信号脉内调制识别方法的代表,为了便于性能对比,直接比较信号总识别成功率的优劣。信号参数设定同第3小节,仿真实验结果如图12所示。

图12 各类信号总识别成功率
图12中,本文算法在SNR取-3 dB时已经超过90%识别成功率,而文献[1]算法达到90%识别成功率需要的最小SNR为6 dB,文献[2]所需SNR则为3 dB。本文算法对SNR要求最低,因此识别调制类型的性能优于其他两种方法。
5.4 信号脉宽减小对算法性能影响
信号脉宽取值在3~5 μs时,图13给出了信号识别正确率曲线。SNR≥-3 dB时各个信号识别正确率仍在90%以上,但CP信号和BPSK信号曲线有波动而QPSK则保持稳定。这是由于脉宽减小而采样率不变,采样点数减少到原来的三分之一,导致时频曲线点数骤减,峰值点检测受到一定程度的影响,NP值有波动从而导致BPSK和CP信号识别曲线小范围波动。而QPSK信号的NP值较大,即使有波动也能保持大于6,因此QPSK识别率保持稳定。
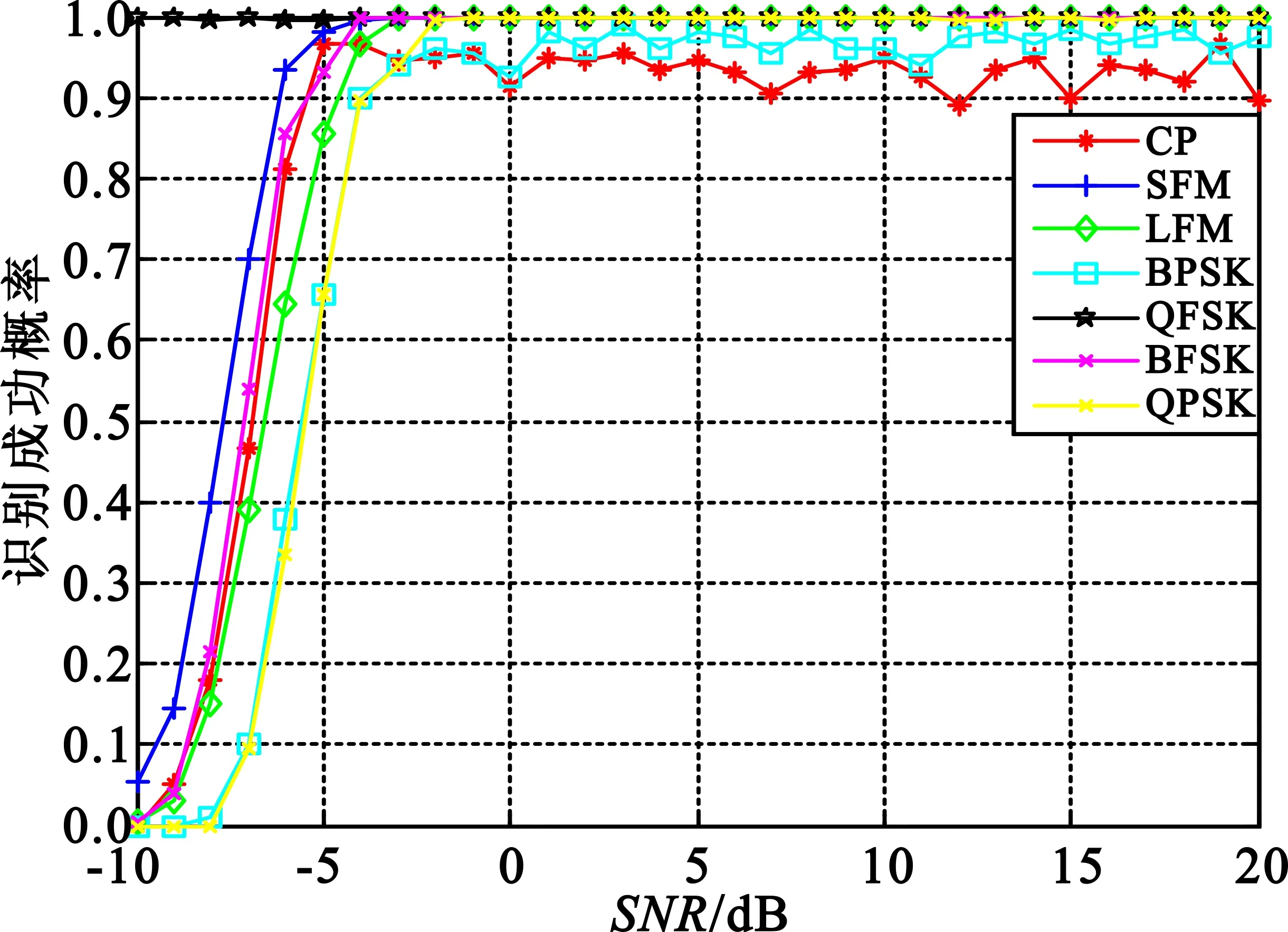
图13 窄脉宽时各类信号识别成功率
实验表明脉宽取值减小时,信号在STFT时窗中的有效部分减少,相应的分辨率和精度都要下降,使得各类信号识别成功率降低。尤其是CP与BPSK信号,脉宽为2.5 μs,在SNR为-3 dB时识别正确率低至60%,其他信号识率也在70%左右。因此对于窄脉宽信号,识别效果差一些,这是本方法的局限之处。通过减小STFT窗长以及增大采样率等方法来增加IF的点数,一定程度上可以提高识别率;缺点是IF精度下降,当STFT点数很小时,识别率反而更低。总之,通过适当提高采样率来增加采样点数,虽不能从根本上解决问题,但可以在一定程度上提高窄脉冲调制识别性能。
6 结束语
瞬时频率特征能体现信号脉内调制的规律,通过提取IF及其特征量可以对信号进行识别。本文首先通过STFT提取出各信号的时频特征,然后通过对瞬时频率进行两级归一化处理提取其均值和标准差等作为识别信号的特征量,最后分析雷达信号特征量取值规律,确定各个特征量的门限并建立信号分类识别流程。仿真实验表明,对于典型的7种雷达信号,当信噪比高于-3 dB时,识别成功率在90%以上。采用STFT提取瞬时频率提高了算法的实时性,能够使接收机对脉宽大于3 μs雷达信号进行快速脉内调制识别,具有工程应用价值。对于脉宽3 μs以下信号调制识别,还需进一步研究。
[1] 普运伟,金炜东,胡来招. 基于瞬时频率二次特征提取的辐射源信号分类[J].西南交通大学学报,2007,42(3):373-379. PU Yunwei,JIN Weidong,HU Laizhao. Automatic classification of radar emitter signals based on cascade feature extractions[J].Journal of Southwest Jiaotong University,2007,42(3):373-379.(in Chinese)
[2] 毕大平,董灰,姜秋喜. 基于瞬时频率的脉内调制识别技术[J].电子对抗技术,2005,3(2):6-9. BI Daping,DONG Hui,JIANG Qiuxi. Inpulse modulation identification technique by the instant frequency[J].Electronic Information Warfare Technology,2005,3(2):6-9.(in Chinese)
[3] 刘康宁.基于时频分析的雷达信号调制方式识别技术研究[D].西安:西安电子科技大学,2014. LIU Kangning. Research on identification of the radar signal based on time-frequency analysis[D].Xi′an:Xidian University,2014.(in Chinese)
[4] PERSSON C.Classification and analysis of low probability of intercept radar signals using image processing[D].Monterey,California:Naval Post-graduate School,2003:49-86.
[5] RU X H,LIU Z,JIANGW L,et al. Recognition performance analysis of instantaneous phase and its transformed features for radar emitter identification[J].IET Radar Sonar Navigation,2015,10(5):945-952.
[6] ZHU J,ZHAO Y,TANG J. Automatic recognition of radar signals based on time-frequency image character[C]//Proceedings of 2013 IET International Radar Conference.Xi′an:IEEE,2013:1-6.
[7] DOBRE O A,ABDI A,BAR-NESS Y,et al. Blind modulation classification:a concept whose time has come[C]//Proceedings of 2005 IEEE Sarnoff Symposium on Advances in Wired and Wireless Communications.Princeton,NJ:IEEE,2005:223-228.
[8] 王晓峰,邢敏捷,刘歌,等. 基于改进 DFT 相位差的正弦波频率估计[J].电讯技术,2016,56(10):1129-1133. WANG Xiaofeng,XING Minjie,LIU Ge,et al. Sinusoidal signal frequency estimation based on improved DFT phase difference[J].Telecommunication Engineering,2016,56(10):1129-1133.(in Chinese)
An Effective Method for Fast Recognizing Radar Signals
YANG Jian,ZHOU Tao,HE Zi'ang
(Science and Technology on Electronic Information Control Laboratory,Chengdu 610036,China)
Aiming at the problem of low success rate of radar signal detection and recognition,this paper proposes a new algorithm for radar signal recognition based on instantaneous frequency feature extraction. Firstly,the algorithm uses short time Fourier transform(STFT) to calculate every part of the signal’s instantaneous frequency characteristic. Secondly,it calculates the once and twice normalized instantaneous frequency characteristic value. Finally,it uses hierarchical decision-making method to conduct radar signal classification. Simulation results show that the proposed method can effectively identify all kinds of radar signal.The recognition success rate is more than 90% when the signal-to-noise ratio(SNR) is higher than -3 dB.
radar signal recognition;instantaneous frequency;feature extraction;short time Fourier transform;intra-pulse modulation
10.3969/j.issn.1001-893x.2017.04.009
杨建,周涛,何梓昂.一种有效的雷达信号快速识别方法[J].电讯技术,2017,57(4):418-424.[YANG Jian,ZHOU Tao,HE Zi'ang.An effective method for fast recognizing radar signals[J].Telecommunication Engineering,2017,57(4):418-424.]
2016-08-12;
2016-12-23 Received date:2016-08-12;Revised date:2016-12-23
TN971.1
A
1001-893X(2017)04-0418-07

杨 建(1989—),男,河北沧州人,硕士研究生,主要研究方向为信号与信息处理;
Email:yangjianl4029@163.com
周 涛(1978—),男,陕西汉中人,2003年于浙江大学获博士学位,现为高级工程师,主要研究方向为电子对抗、高速信号处理、高速光电采样等;
何梓昂(1983—),男,四川巴中人,2008年于浙江大学获硕士学位,现为工程师,主要研究方向为电子侦察、高速信号处理。
*通信作者:yangjianl4029@163.com Corresponding author:yangjianl4029@163.com
