网络结构异质性对疾病传播影响的初步研究
2017-04-26王宁宁
王宁宁
(中北大学 理学院, 太原 030051)
网络结构异质性对疾病传播影响的初步研究
王宁宁
(中北大学 理学院, 太原 030051)
为研究网络结构异质性对疾病传播的影响,基于N-intertwined模型构建出连续时间的异质SIS模型,分析模型解存在唯一性条件和传播阈值,并得到模型零解全局稳定性。由传播阈值与邻接矩阵谱半径的关系,分析出网络结构影响疾病传播的主要因素。由ER随机网络和BA无标度网络的数值模拟,验证了疾病更容易在无标度网络中传播。通过数值模拟得出:当初始阶段个体染病概率相同或某一社团存在局部传染源时,无标度网络社团之间的耦合强度不会影响最终染病人数,但会促进或抑制疾病传播;而相对于无社团结构的无标度网络,社团结构的存在会缩短染病人数达到平衡的时间。
复杂网络;疾病传播;结构异质;谱半径
随着复杂网络传播动力学的不断发展,网络模型成为研究信息、疾病传播途径的有效工具。对于疾病传播,目前存在平均场方法、节点状态对逼近法和渗流理论[1-3]等方法。除上述研究方法外,还有一类节点状态建模法[4-5],其经典模型是N-intertwined SIS模型。该模型通过网络中个体染病概率的变化,反映网络中染病者人数的增减。一般地,N-intertwined模型根据时间尺度可分为离散时间模型和连续时间模型。对于前者,单位时间内个体染病和恢复事件是否可同时发生存在争议[5- 6];而后者在某些文献中弱化了网络结构的异质性[4],将个体染病概率等同于个体每个邻居对其传染率的期望,这显然是对个体染病概率的不精确估计。因此,本文综合两种建模方式的优点,建立了连续时间上体现网络异质性的常微分方程模型,并以此作为本文网络疾病传播的基本工具。
在网络拓扑结构方面,不同类型的网络对疾病传播也具有不同的影响。以随机网络为例,当节点间连边概率固定时,网络中节点度分布服从泊松分布[7]。然而,对于无标度网络而言,节点度分布服从幂律分布。这就使得在节点总数、平均度等拓扑参数相同时,网络结构存在明显的异质性。仅对无标度网络而言,当基本参数相同时,其网络内部还有可能存在社团结构,使得部分节点内部连接稠密而外部连接稀疏,这些结构差异都有可能改变疾病在网络中的传播特性。本文从数学分析角度出发,建立异质网络疾病传播的SIS模型,通过分析得出随机网络和无标度网络对疾病传播的影响。并通过数值模拟验证随机网络和无标度网络疾病传播的差异,分析耦合强度不同的社团结构对疾病流行速率的影响,排除无效预防策略,给出减少染病总数有效的预防策略。
1 异质网络SIS模型的建立及分析
建立异质网络SIS模型,其中节点的状态分为两种:易感状态I和染病状态S。通过该SIS模型研究其染病概率及染病人数I的变化。设λ,μ分别为单位时间内疾病沿一条边的传染率和个体恢复率,将pi(t)记为t时刻节点i的染病概率,N为网络规模[8]。根据Mieghem[4]和Valdano[5]等的建模思想,可知每个节点染病概率的变化与自身疾病的恢复和邻居节点的传染存在必然联系。由此得到如下SIS模型:
(1)
其中A是网络邻接矩阵。假设网络中节点最小度不小于2,则系统(1)的展开式为
(2)
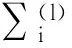

(3)
其中:
由于
(4)
所以,系统(1)的矩阵形式为
(5)
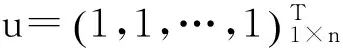
(6)
易知, f (t,p)是G⊆R×Rn的连续函数,且f关于p满足局部Lipschitz条件:
对于∀(t,p1),(t,p2)∈G0,存在P0(t, p0)∈G使得
成立。
简要的证明过程如下:
将 f (t,p1), f (t,p2)分别代入上式,得到
(7)
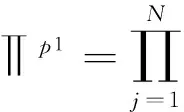
(8)
由于p1,p2都是p0领域内的两个向量,所以必然存在依赖于p0的L,使得L‖p2-p1‖=‖u-p1‖成立。于是由以上不等关系可得
(9)
其中,Lp0=2+μ+L。
综上所述,系统(1)满足解的存在唯一性条件。接下来,通过分析系统的线性部分

(10)
得到疾病的传播阈值。由系统(2)可知,对任意染病概率和染病率存在
证明
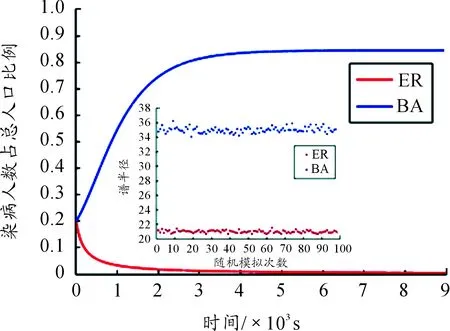
区间U={(p1,p2,…,pn)|0 通过适当放缩,可知 1) 当ki是奇数时, 2) 当ki是偶数时, 因此,线性系统(10)零解局部稳定性与系统(1)相同。即原点附近初始条件相同时,线性系统染病人数趋于零,必然能得到系统(1)染病人数也趋于零。令ρ(-μE+λA)<0,则传播阈值为: (11) 将系统(1)作为系统(10)的扰动系统,扰动项为 如果两个系统零解的稳定性相同,只需证明 (12) 对欧式范数而言, 任取上式中的一项 综上所述,系统(1)与系统(10)零解的局部和全局稳定性均相同。由文献[9]可知,随机网络和无标度网络中邻接矩阵谱半径的估计值分别为 (13) 当网络规模较大且平均度相同时,无标度网络中的疾病传播阈值更有可能小于随机网络,这就降低了疾病在无标度网络中的传播条件,使得疾病更容易在无标度网络中传播。此外,对无标度网络而言,其内部存在独有的社团结构。这种结构内部连接稠密而外部连接稀疏,如图1所示。S.Fortunato等在研究社团结构时,给出了描述节点社团内外度划分混合参数μ的定义[10-11] (14) 图1 无标度网络中有无社团结构的差异 本节进行3组对比试验,分别研究网络结构类型、社团耦合强度和染病个体分布对染病人数和变化速率的影响。 2.1 随机网络和无标度网络疾病传播特性分析 在以下数值分析中,规定实验网络规模为1 000,平均度〈k〉=20且无标度网络幂律分布指数相同,含有社团结构的LFR基准图[10-12]中社团规模也相同。在上述基础上,先进行第一组对比实验,即ER随机网络和BA无标度网络中疾病传播的研究。通过随机构造以上两种网络,得到了平均度相同时的谱半径结果,如图2子图。 图2 阈值介于随机网络和无标度网络阈值 条件之间时染病人数的变化,其中子图是 平均度相同时随机网络与无标度网络的谱半径 由模拟结果可知:平均度相同时,随机网络谱半径的确要比无标度网络谱半径小。因此,当恢复率和染病率之比介于两者谱半径之间时,推断疾病有可能在随机网络中逐渐灭绝,而在无标度网络中传播。为验证这一推断,对系统(1)进行数值模拟,不妨设初始阶段个体染病概率全部相同,染病率和恢复率对随机网络满足条件(10),结果见图2。由结果可知:尽管染病人数占总人数的20%,随机网络中的染病数量仍然可以趋近于0。但是无标度网络中染病人数大约占到了85%。这也证明了上述分析的正确性。 2.2 无标度网络中社团结构对疾病传播的影响 对于无标度网络而言,网络中的社团结构虽然不会直接影响传播阈值,但其仍起到不可忽视的特殊作用。接下来进行第二组对比实验,首先研究平均度、节点度、染病概率和社团规模幂律分布指数等参数相同时,混合参数μ=0.1~0.8时对染病数量的影响。当染病率和恢复率超过或低于阈值条件时,得到数值结果见图3(a)~(b)。由计算结果可以直观看出:初始时刻个体染病概率相同时,不同混合参数μ对染病人数几乎没有影响,但染病人数变化率多少会受到影响。与图2中结果相比,当疾病流行时,网络中社团结构在一定程度上缩短了染病人数稳定所需时间,且耦合强度的增加会促进疾病的快速传播;而当疾病逐渐灭绝时,社团耦合强度的增加会抑制疾病的过早灭绝。接下来,研究当网络中仅存在局部传染源时,社团结构对疾病传播的影响。 图3 初始时刻节点染病概率相同时,社团耦合 强度对疾病灭绝和传播的影响 图4 初始时刻仅存在局部传染源时,社团耦合 强度对疾病灭绝和传播的影响 在第3组对比实验中,随机挑选同一社团中度最大的几个节点作为局部传染源,研究混合参数对染病人数的影响。从数值模拟结果发现:混合参数μ对最终染病人数仍然没有影响,但当疾病流行时,混合参数明显改变了染病人数变化率。在混合参数由0.1变为0.8的过程中,染病人数的变化趋势显著加快,如图4(a)所示。相反,当染病人数逐渐减少时,混合参数对染病人数变化起到了一定抑制作用,如图4(b)所示。相同条件下,对无社团结构的局部传染源进行数值分析,发现无论耦合强度大小,社团结构的存在缩短了疾病流形或灭绝的时间,见图5。综合而言,混合参数μ不会改变最终染病人数的数量,但其数值的增加会促进疾病传播或抑制疾病消亡的速度。 图5 初始时刻仅存在局部传染源时,不存在 社团结构的无标度网络中染病人数变化过程 本文通过建立异质网络SIS模型,证明了系统解的存在唯一性和疾病传播的阈值条件,并得到零解的全局稳定性。以此为基础,研究了随机网络和无标度网络疾病传播阈值的差异。通过数值模拟发现:当初始个体染病概率相同或某一社团出现局部单一传染源时,混合参数μ均不会影响染病人数,但是会改变染病人数的变化率。相对于无社团结构的无标度网络,无论耦合强度多大,社团结构的存在都会缩短疾病传播的时间。因此,对无标度网络而言,适当减弱各个社团之间的耦合强度或破坏存在的社团结构可以减慢疾病的快速蔓延,为控制疾病传播策略的制定赢得时间。但在不改变阈值条件时,上述预防策略不能从根本改变最终的染病人数[13-14]。为得到有效抑制疾病传播范围的方法,需要寻找降低网络谱半径或改变网络拓扑类型的预防策略,其中重视个体自适应性或适当隔离高危人群就是有效途径[15-17]。 [1] PASTOR-SATORRAS R,VESPIGNANI A.Epidemic Spreading in Scale-Free Networks[J] Phys.Rev.Lett,2001,86:3200. [2] MATSUDA H,OGITA N,SASAKI A,et al.Statistical mechanics of population:The lattice Lotka-Volterra model[J].Progress in Theoretical Physics,1992,88:1035. [3] COHEN R,EREZ K,AVRAHAM B,et al.Resilience of the Internet to Random Breakdowns[J].Phys.Rev.Lett,2000,85:4626. [4] MIEGHEM P V.The N-intertwined SIS epidemic network model[J].Computing,2011,93:147. [5] VALDANO E,FERRERI L,POLETTO C,et al.Analytical Computation of the Epidemic Threshold on Temporal Networks[J].Phys.Rev.X,2015,5:021005. [6] WANG Y,CHAKRABARTI D,WANG C,et al.Epidemic spreading in real networks:an eigenvalue viewpoint[J].Proceedings of the IEEE Symposium on Reliable Distributed Systems,2003,10:25. [7] 汪小帆.网络科学导论[M].北京:高等教育出版社,2012. [8] SCHWARZKOPF Y,RáKOS A,MUKAMEL D.Epidemic spreading in evolving networks.[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2010,82(3 Pt 2):336-354. [9] FAN Chung,LU Linyuan,VAN Vu.The Spectra of Random Graphs with Given Expected Degrees[J].Proceedings of the National Academy of Sciences of the United States of America,2003,100(11):6313-8. [10]LANCICHINETTI FORTUNATO S,RADICCHI F.Benchmark graphs for testing community detection algorithms[J].Phys.Rev.E,2008,78:046110. [11]FORTUNATO S,LANCICHINETTI A.Community detection algorithms:A comparative analysis[J],Phys.Rev.E,2009,80:056117. [12]FORTUNATO S.Community detection in graphs[J].Physics Reports,2010,486(3-5):75-174. [13]ZHANG J P,JIN Z.Epidemic spreading on complex networks with community structure[J].Applied Mathematics & Computation,2012,219(6):2829-2838. [14]PAN W,SUN G Q,JIN Z.How demography-driven evolving networks impact epidemic transmission between communities[J].Journal of Theoretical Biology,2015,382:309-319. [15]SCHWARZKOPF Y,RKOS A,MUKAMEL D.Epidemic spreading in evolving networks[J].Phys Rev E,2010,82:336. [16]CALDARELLI G,CAPOCCI A,LRP D,et al.Scale-Free Networks from VaryingVertex Intrinsic Fitness[J],Phys Rev Lett,2002:89:25. [17]REN G,WANG X.Epidemic spreading in time-varying community networks.[J].Chaos,2014,24(2):297-302. (责任编辑 刘 舸) Primary Study About the Effect of Network Structure Heterogeneity on Epidemic Spread WANG Ning-ning (School of Science, North University of China, Taiyuan 030051, China) In order to study the effect of network structure heterogeneity, an epidemic SIS network model was established based on the N-intertwined model. Subsequently, we proved the existence and uniqueness of solution and obtained the epidemic threshold, and then the globally asymptotically stability of zero solutions was also concluded. From the relationship between the threshold and the spectral radius of network, we studied out the main reason about the influence of the network structure on epidemic spread. Through the simulation of the ER and BA network, the easier spread of epidemic was verified in the BA network. When the infection probability is equal to each individual or there are some local infection sources in one community, the coupling strength of communities is irrelevant to the final number of patients, but will promote or restrain the spread. Compared with the scale-free network without communities, the existence of communities is beneficial to reduce the time needed to balance. complex network; epidemic spread; structure heterogeneity; spectral radius 2017-01-16 国家自然科学基金资助项目(11331009) 王宁宁(1991—),男,河北泊头人,硕士研究生,主要从事复杂网络研究,E-mail:nnwangnuc@foxmail.com。 王宁宁.网络结构异质性对疾病传播影响的初步研究[J].重庆理工大学学报(自然科学),2017(4):121-126. format:WANG Ning-ning.Primary Study About the Effect of Network Structure Heterogeneity on Epidemic Spread[J].Journal of Chongqing University of Technology(Natural Science),2017(4):121-126. 10.3969/j.issn.1674-8425(z).2017.04.020 O175;O41 A 1674-8425(2017)04-0121-06




2 异质网络SIS模型数值解及其分析



3 结束语
