空位缺陷对β-AgVO3电子结构和光吸收性能的影响∗

任超 李秀燕 落全伟 刘瑞萍 杨致 徐利春

(太原理工大学物理与光电工程学院,晋中 030600)

1 引 言

过去几年来,银钒氧化物在锂电池[1,2]、抗菌水性涂料添加剂[3]、气体传感器[4]和光催化领域[5−8]都受到了广泛的关注,这类材料的典型代表是AgVO3,AgVO3在自然界中存在两种稳定相:α-AgVO3相和β-AgVO3相.两者都是单斜晶相,α-AgVO3相空间群为C2/c,β-AgVO3相空间群为Cm.但α-AgVO3相在200°C时会不可逆转地转变成β-AgVO3相[9],所以在通常实验中制备的AgVO3多为β-AgVO3相,对β-AgVO3的利用与研究也更为广泛.

Feng等[10]研究了β-AgVO3的电性能,发现β-AgVO3具有典型的p-型半导体特性,文中推测原因是由于β-AgVO3晶体中存在的Ag空位和O空位引起的.Zhao等[5]通过在室温条件下用NaBH4还原β-AgVO3,发现可以把β-AgVO3中的Ag离子还原成Ag纳米颗粒并吸附在β-AgVO3表面,形成Ag/AgVO3纳米带,与β-AgVO3相比具有更强的光催化活性.解释其原因一是Ag纳米颗粒的存在引起等离子体表面共振,有效抑制了晶体中光生电子-空穴对的复合,提升光生电子-空穴对的迁移率,从而使Ag/AgVO3光催化活性提高;原因二是Ag/AgVO3的带隙值(1.51 eV)比β-AgVO3的带隙(2.11 eV)要低,更容易对可见光发生响应.最近de Oliveira等[11]通过实验和计算两种手段对Ag/AgVO3中表面Ag纳米颗粒的形成过程进行研究,Ag纳米颗粒是在电子束照射下,β-AgVO3中[AgOx]团簇与入射的电子相互作用得到的.这些研究成果都表明了实验制备得到的Ag/AgVO3晶体中有Ag空位的存在,Ag空位存在也对晶体性质产生了影响,但是并没有做进一步探究.氧化物在制备过程中通常会形成O空位缺陷,我们也应考虑β-AgVO3中O空位对其性质的影响.此外,还需考虑Ag-O双空位对晶体性质的影响.

本文利用密度泛函理论框架下的广义梯度近似(GGA+U)平面波超软赝势方法分别对β-AgVO3晶体、含有Ag空位(VAg)的β-AgVO3晶体、含有O空位(VO)的β-AgVO3晶体和含有Ag,O双空位(VAg-O)的β-AgVO3晶体进行了几何结构优化,计算了它们的能带结构、态密度、差分电荷密度和光吸收谱图,得出晶体中存在VAg,VO或VAg-O时对其电子结构和光学性质的影响.

2 理论模型和计算方法

本文计算所采用的模型是单斜β-AgVO3结构,空间群是Cm.首先选取β-AgVO3晶胞结构进行计算,共40个原子.在模拟空位缺陷时用1×2×1的超晶胞,共有80个原子,去掉其中的一个Ag原子或者O原子进行计算,Ag空位和O空位浓度都是1.25%.由于传统的密度泛函理论计算(LDA和GGA)是一种基态理论,不能精确地用来描述过渡族元素氧化物的带隙.在VASP软件中可以通过引入能够描述原子间强相关作用项来代替GGA的计算,即在模型中通过Hubbard参数U(排斥能)来描述这种强相关作用,称为GGA+U方法.GGA+U[12]方法能够比较精确地描述过渡族元素氧化物的带隙.本文采用GGA+U方法计算,选取500 eV作为平面波的截断能,力收敛标准为0.03 eV/nm,能量收敛标准为1.0×10−5eV,计算晶胞时采用Monkhorst-Pack方案自动生成4×18×8的K点,在含有空位缺陷时选择4×9×8的K点.

3 结果与讨论

3.1 完整晶体

先采用广义梯度近似下Perdew-Burke-Ernzerhof泛函进行结构优化和计算,得出β-AgVO3晶体带隙值为1.33 eV,与实验值2.11 eV有较大的差别.为使计算结果更加可信,我们采用GGA+U方法进行修正,通过查询文献[13]和取值计算之后,发现当V的3d轨道电子的U值为UV=2.7 eV,Ag的4d轨道电子的U值为UAg=6 eV时,能很好地符合实验值.

分别利用GGA和GGA+U方法得出的β-AgVO3完整晶体的晶格常数和带隙值见表1,表中同时列出了各项的实验结果[8].从表1可以看出,GGA+U方法得到的晶格常数与带隙值更接近实验值.图1分别给出了GGA和GGA+U方法计算得到的态密度图,可以看出完整晶体β-AgVO3的带隙由1.33 eV变为2.11 eV,两种方法计算得出的价带顶能级都是由Ag-4d和O-2p杂化形成,导带底的能级都由V-3d轨道提供,与之前文献[5]计算结果相一致,说明本文计算方法的合理性.对比GGA+U方法与GGA方法,GGA+U方法能更好地符合实验值,之后的计算都是在GGA+U方法下进行.

图1 (网刊彩色)β-AgVO3完整晶体的态密度图 (a)GGA方法;(b)GGA+U方法Fig.1.(color online)Calculated density of states for perfect β-AgVO3obtained by the(a)GGA and(b)GGA+U methods,respectively.

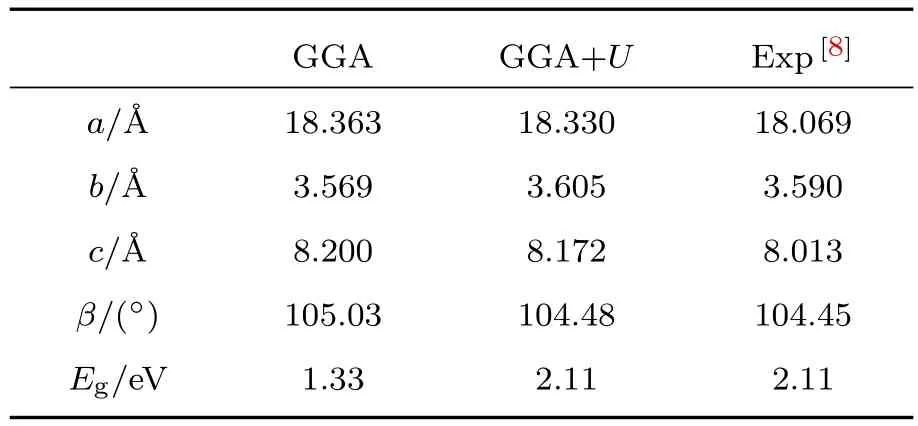
表1 GGA方法和GGA+U方法得出的β-AgVO3晶体的晶格常数和带隙值Table 1.Calculated lattice parameters and band gap of β-AgVO3obtained by the GGA and GGA+U methods,respectively.

3.2 空位形成能计算

我们计算了不同位点的VAg和VO的形成能,找出形成能最低的位点来确定空位在晶体中的形成位置.Ag空位和O空位形成能分别用EAg,f和EO,f表示:

其中,E(Ag,defect)和E(O,defect)分为含有Ag空位和O空位时缺陷体系的总能量,E(perfect)是完整晶体β-AgVO3的总能量,E(Ag)是金属Ag单质的能量,E(O2)是O2的能量,n代表完整晶体中去掉的Ag原子个数,m代表在完整晶体中去掉的O原子个数.本文选择n和m均为1进行计算.

我们首先对Ag原子的位点进行分类,图2(a)是β-AgVO3晶胞的球棍模型,图2(b)是β-AgVO3晶胞的多面体模型.通过图2(b)可以发现,β-AgVO3晶胞中有四个不同的Ag位点[14],记为Ag1,Ag2,Ag3和Ag4.Ag1的周围有6个O原子,Ag2,Ag3周围各有5个O原子,Ag4周围有7个O原子.由于Ag4的存在,破坏了体系的中心对称性,使得Ag2原子和Ag3原子不同.而O原子的个数较多,有12个,这里不一一指出.本文计算了包括4个不同的Ag位点和12个不同的O位点的形成能.

表2和表3分别列出了不同VAg和不同VO的缺陷形成能.由表2可以得出Ag3空位的总能量最低,对应形成能最低,表明了Ag3空位在晶体中最容易形成,并且Ag2空位和Ag3空位的形成能相差较小,原因是Ag2和Ag3周围的环境类似,而Ag4空位形成能最高,说明Ag4空位最难形成.文献[11]已得到类似的结果:在β-AgVO3晶体中Ag纳米颗粒的产生较容易由Ag2原子和Ag3原子聚集而成,Ag4原子最难在晶体中脱离.从表3中我们可以得到O1空位形成能最低,说明O1空位更容易在晶体中形成.另外,对比表2和表3,可以看出EAg,f比EO,f更低,表明在β-AgVO3晶体中VAg比VO更容易形成,晶体中应存在有较多的VAg.

图2 (网刊彩色)(a)β-AgVO3的球棍模型;(b)β-AgVO3的多面体模型;绿色小球为Ag原子,灰色小球为V原子,红色小球为O原子Fig.2. (color online)(a)Ball-and-stick model of β-AgVO3;(b)polyhedral model of β-AgVO3.The Green,grey and red balls represent Ag,V and O atoms,respectively.

表2 不同VAg位点的β-AgVO3的总能和形成能Table 2.Total energies and formation energies of β-AgVO3with different Ag vacancies.

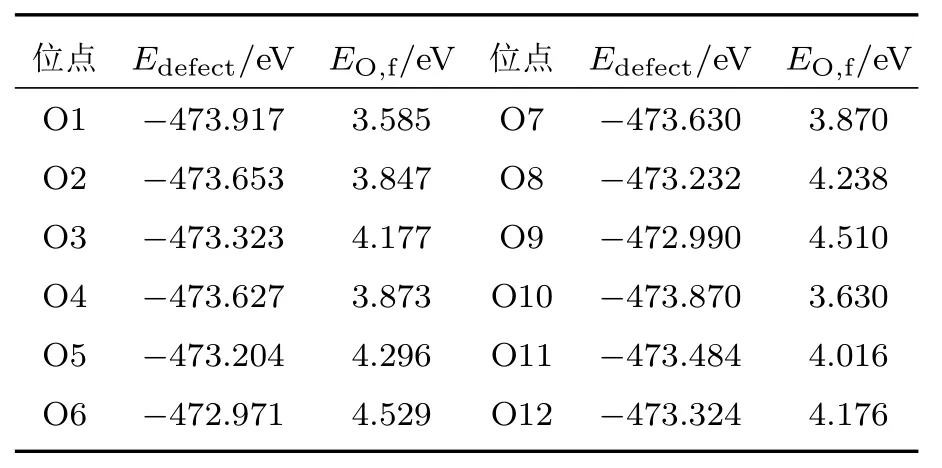
表3 不同VO位点的β-AgVO3的总能和形成能Table 3.Total energies and formation energies of β-AgVO3with different O vacancies.

3.3 电子结构分析

我们接下来对含有Ag3空位、O1空位和Ag3-O1双空位的β-AgVO3的超晶胞模型做了进一步的计算,以探究空位缺陷对晶体的电子结构影响.图3是Ag3空位、O1空位和Ag3-O1双空位的β-AgVO3超晶胞模型.

图3 (网刊彩色)含有空位缺陷的β-AgVO3超晶胞模型(a)Ag3空位;(b)O1空位;(c)Ag3-O1双空位Fig.3. (color online)The supercell models of β-AgVO3with vacancy defect:(a)Ag3 vacancy;(b)O1 vacancy;(c)Ag3-O1 bivacancy defect.

基于前面对空位形成难易程度的讨论,我们分析了Ag3空位、O1空位与Ag3-O1双空位对β-AgVO3电子结构性质的影响.图4(a),(c),(e)和(g)分别为完整的、含有一个Ag3空位、含有一个O1空位及含有Ag3-O1双空位的β-AgVO3晶体能带结构,图中红色虚线表示费米能级,并且调整为0 eV;图4(b),(d),(f)和(h)为对应的态密度图.我们计算得到完整的β-AgVO3晶体带隙为2.11 eV(如图4(a)),与文献[8]结果符合得比较好.从图4(c)可以看出,引入Ag3空位后,费米能级下移穿过Ag-4d和O-2p轨道,β-AgVO3呈现p-型半导体性质;由于价带顶处能级的分裂以及空位杂质能级的出现,价带顶能级相比于完整β-AgVO3晶体有一定的上升,导致带隙稍微减小(2.00 eV).同样,从图4(e)我们得到引入O1空位后,费米能级上移穿过V-3d轨道,β-AgVO3呈现n-型半导体性质;由于O1空位缺陷的存在,V-3d能级出现分裂导致带隙降低(1.90 eV).当引入Ag3-O1双空位后,费米能级上移穿过V-3d轨道,β-AgVO3晶体呈现n-型半导体性质,带隙减小为1.70 eV.通过前文的分析我们已经知道,Ag空位的形成能比O空位低,说明在β-AgVO3中更容易出现Ag空位,所以β-AgVO3一般表现为p-型半导体性质,这与实验证明β-AgVO3是p-型半导体[10]相符.比较图4(b),(d),(f)和(h)所示态密度图可以看出,空位的引入对价带顶和导带底态密度影响不大,价带顶都是由Ag-4d和O-2p杂化形成,导带底主要由V-3d轨道提供.

3.4 Bader电荷分析

空位体系费米能级的移动意味着空位缺陷的存在使得β-AgVO3晶体中发生了电荷转移,我们可以通过Bader电荷来进行分析,图5(a)—(c)分别给出了含有VAg,VO和VAg-O缺陷的β-AgVO3晶体的差分电荷密度图,可以看到主要是空位周围的原子发生了电荷重新分布.为了定量地分析电荷转移量,分别对VAg,VO和VAg-O空位周围的原子进行了Bader电荷分析.当Ag3空位存在时,主要是空位周围的Ag原子和O原子的电荷分布发生了变化.与完整的β-AgVO3晶体相比,空位周围的Ag原子和O原子的电荷量都有所减少,表4列出了完整β-AgVO3晶体和Ag3空位存在时晶体中相应O原子和Ag原子外围电子层电荷量的变化情况.当O1空位存在时,空位周围的O,Ag和V原子都有不同程度的电荷转移,与完整的β-AgVO3晶体相比,O1空位周围的O,Ag和V原子的电荷量都有所增加,各原子外围电子层电荷量及与完整β-AgVO3晶体的对照情况见表5.当Ag3-O1双空位存在时,空位周围的V原子和O原子的电荷量有所增大,各原子外围电子层电荷量与完整晶体的对照情况见表6.

图4 (网刊彩色)晶体的能带结构和态密度图 (a),(b)β-AgVO3晶体;(c),(d)含有Ag3空位的 β-AgVO3晶体;(e),(f)含有O1空位的β-AgVO3晶体;(g),(h)含有Ag3-O1双空位的β-AgVO3晶体Fig.4.(color online)Calculated band structure and density of states for β-AgVO3:(a),(b)No defect;(c),(d)with Ag3 vacancy;(e),(f)with O1 vacancy;(g),(h)with Ag3-O1 bivacancy.

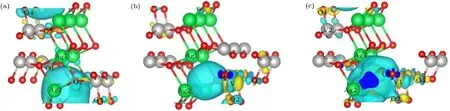
图5 (网刊彩色)(a)Ag3空位,(b)O1空位和(c)Ag3-O1双空位周围的差分电荷密度分布(图中的电荷密度等高值选取0.003 e/Å3,蓝色代表失去电子,黄色代表得到电子)Fig.5.(color online)Calculated partial charge density distributions around the(a)VAgdefect,(b)VOdefect and(c)VAg-Odefect.An isovalue of 0.003 e/Å3is used,and the blue and yellow isosurfaces represent negative and positive values of electron density in space,respectively.

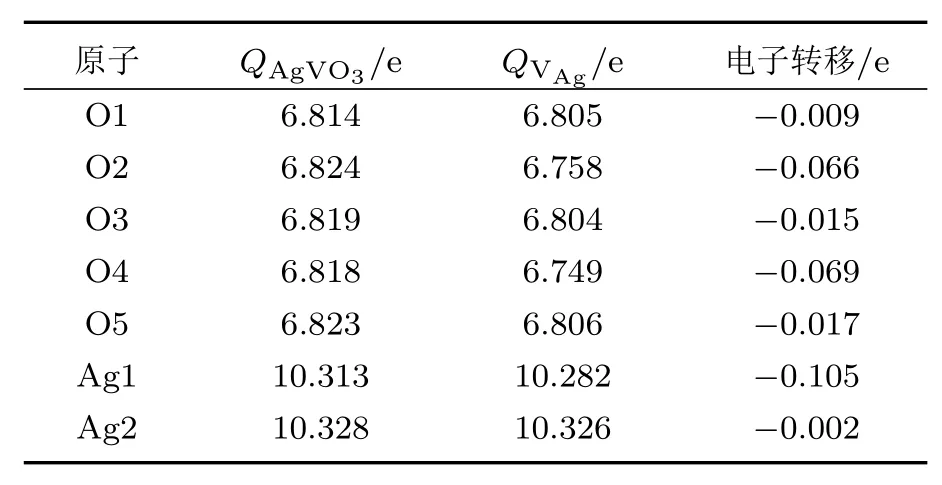
表4 Ag3空位周围原子的外层电子分布变化Table 4.Outer electron distributions in the atoms around Ag3 vacancy.

表5 O1空位周围原子的外层电子分布变化Table 5.Outer electron distributions in the atoms around O1 vacancy.

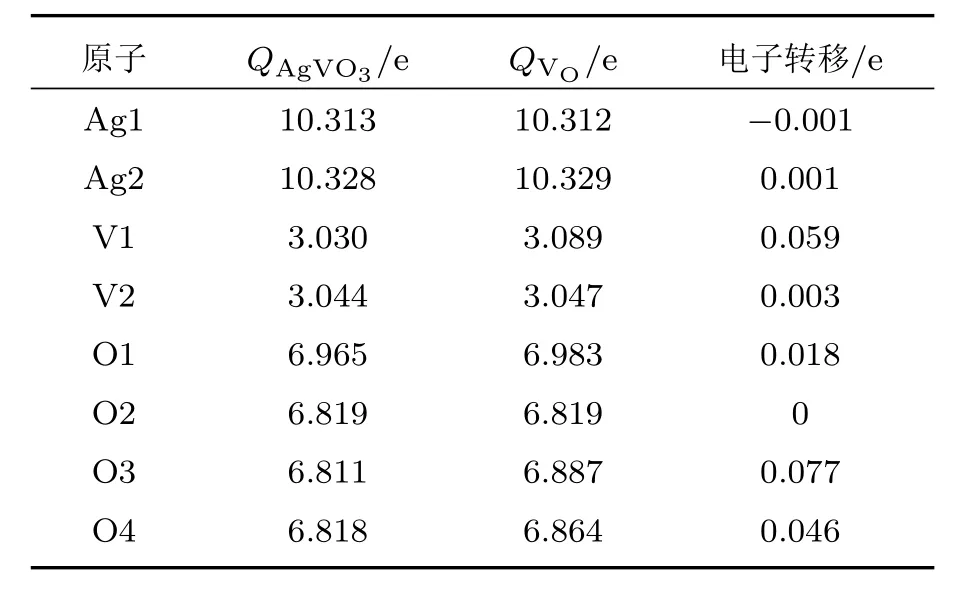
表6 Ag3-O1双空位周围原子的外层电子分布变化Table 6.Outer electron distributions in the atoms around Ag3-O1 bivacancy.

3.5 吸收光谱分析

电磁波在介质中传播,当需要考虑吸收影响时,介电函数要用复数ε(ω)=ε1(ω)+iε2(ω)来描述,可以利用计算占据态和非占据态波函数的矩阵元素得到介电函数虚部ε2(ω)[15,16]:

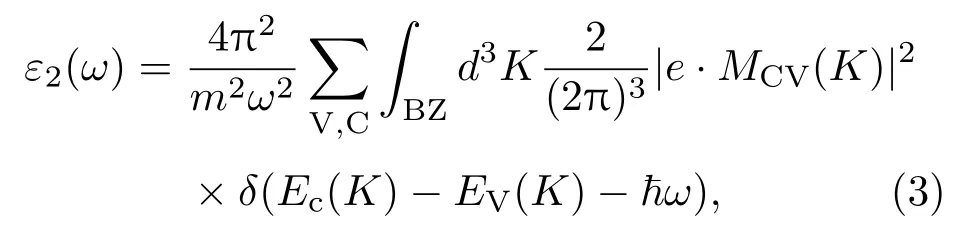
式中,下标C,V分别表示导带和价带,BZ为第一布里渊区,K为倒格矢,|MCV(K)|为动量矩阵元,ω为角频率,EC(K)和EV(K)分别为导带和价带的本征能级.而介电函数实部ε1(ω)则可以利用Kramers-Kroning色散关系求出[17].吸收系数α(ω)可以用ε1(ω)和ε2(ω)推导得出

本文分别计算了完整晶体β-AgVO3、含有Ag3空位、含有O1空位和含有Ag3-O1双空位的β-AgVO3超胞体系下的吸收光谱分布结果如图6所示,本文计算结果与β-AgVO3晶体的紫外可见吸收光谱实验结果[8]符合得很好.当光子能量大于2.11 eV后,吸收系数开始增大,根据能带结构和态密度分析可知,这是由于Ag-4d和O-2p(价带顶)到V-3d(导带底)跃迁产生.分析图6可知,含有VAg,VO和VAg-O缺陷体系与完整体系相比,在可见光范围内没有明显的改变,原因是由于Ag3空位和O1空位的存在对体系的带隙影响并不大.但需要注意的是,含有O1空位和Ag3-O1双空位体系在红外线波段内有明显的响应,这与之前的能带图符合得很好,费米能级上移进入导带,费米能级下的V-3d轨道电子只需吸收较少的能量就能发生带间跃迁.

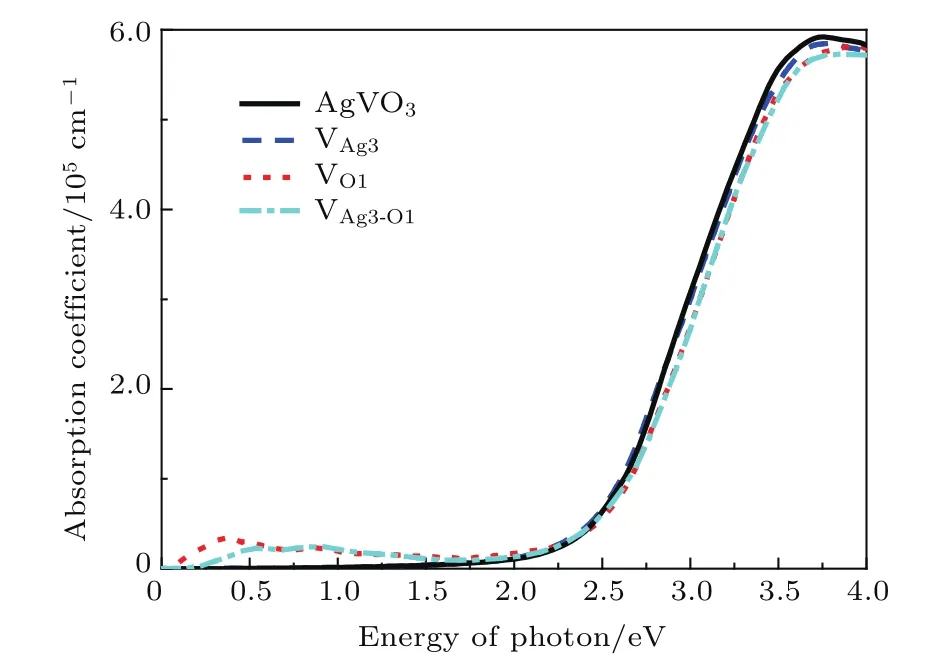
图6 (网刊彩色)β-AgVO3,VAg3,VO1和VAg3-O1的吸收光谱Fig.6.(color online)The absorption spectra for β-AgVO3,VAg3,VO1and VAg3-O1.

4 结 论

本文采用基于密度泛函理论的第一性原理平面波赝势方法研究了β-AgVO3中Ag空位、O空位和Ag-O双空位对其电子结构性质及光吸收性质的影响.在GGA+U方法中,我们确定了V的U值为2.7 eV,Ag的U值为6 eV.通过比较不同Ag空位和O空位的形成能,发现β-AgVO3中主要形成Ag3空位和O1空位,并且Ag空位较O空位更容易形成.计算得到无缺陷的完整β-AgVO3带隙为2.11 eV;当引入Ag3空位时,β-AgVO3带隙减少到2.00 eV,呈现p-型半导体性质;当引入O1空位时,β-AgVO3带隙减少到1.90 eV,呈现n-型半导体性质.通过对吸收光谱分析,我们发现Ag3空位的存在对β-AgVO3晶体在可见光范围内的光吸收影响不大,而O1空位和Ag3-O1双空位的存在会使晶体在红外波段有较明显的光响应.感谢太原理工大学科学云计算中心提供支持.

[1]Zeng H,Wang Q,Rao Y 2015RSC Adv.5 3011

[2]Liang S,Zhou J,Zhang X,Tang Y,Fang G,Chen T,Tan X 2013Cryst.Eng.Comm.15 9869

[3]Holtz R D,Lima B A,Souza Filho A G,Brocchi M,Alves O L 2012Nanomedicine8 935

[4]Mai L,Xu L,Gao Q,Han C,Hu B,Pi Y 2010Nano Lett.10 2604

[5]Zhao W,Guo Y,Wang S,He H,Sun C,Yang S 2015Appl.Catal.B165 335

[6]Zhao W,Liang F,Jin Z M,Shi X B,Yin P H,Wang X R,Sun C,Gao Z Q,Liao L S 2014Mater.Chem.A2 13226

[7]Liang S,Zhou J,Pan A,Zhang X,Tang Y,Tan X,Chen T,Wu R 2013Power Sources228 178

[8]Ju P,Fan H,Zhang B,Shang K,Liu T,Ai S,Zhang D 2013Sep.Purif.Technol.109 107

[9]Kittaka S,Matsuno K,Akashi H 1999Solid State Chem.142 360

[10]Feng M,Luo L B,Nie B,Yu S H 2013Adv.Funct.Mater.23 5116

[11]de Oliveira R C,Assis M,Teixeira M M,da Silva M D P,Li M S,Andres J,Gracia L,Longo E 2016J.Phys.Chem.C120 12254

[12]Sui P F,Dai Z H,Zhang X L,Zhao Y C 2015Chin.Phys.Lett.32 077101

[13]Solovyev I V,Dederichs P H 1994Phys.Rev.B50 16861

[14]Rozier P,Savariault J M,Galy J 1996Solid State Chem.122 303

[15]Shen X C 2002The Spectrum and Optical Property of Semiconductor(Beijing:Science Press)p77(in Chinese)[沈学础 2002半导体光谱和光学性质 (北京:科学出版社)第77页]

[16]Shen J,Wei B,Zhou J,Shen S Z,Xue G J,Liu H X,Chen W 2015Acta Phys.Sin.64 217801(in Chinese)[沈杰,魏宾,周静,Shen Shirley Zhiqi,薛广杰,刘韩星,陈文2015物理学报64 217801]

[17]Sun J,Wang H T,He J L,Tian Y J 2005Phys.Rev.B71 125132