非绝热分子动力学的量子路径模拟

李晓克 冯伟

(天津大学物理系,天津 300350)

1 引 言

由于全量子动力学模拟计算量过大,混合经典-量子分子动力学模拟方法已经被广泛应用于气体分子、势能面系统、生物分子以及超分子系统.在这类系统中,由于原子核质量大小是电子质量的103—104倍,电子速度比原子核速度大3—4个数量级,根据玻恩-奥本海默(BO)近似,可近似认为每一时刻电子运动在静止的原子核势场中,原子核几乎不受电子位置的影响.因此在求解电子的波函数时可将核运动与电子运动分离.在该近似下,利用量子化学等电子结构计算方法,可以得到系统的势能面.若分子始终处于单一势能面上,电子态之间的跃迁可以忽略,这就是所谓的绝热过程.相反,如果势能面相互靠近,在势能面的(近)交叉区可能发生电子态的跃迁,就必须处理非绝热过程.

混合经典-量子分子动力学方法的基本思想是将原子核部分的运动通过牛顿运动方程来处理,而电子部分则用量子力学处理.混合经典-量子分子动力学模拟方法主要有Ehrenfest方法[1−3]、势能面跃迁法[4−9]、二者的混合方法[10−13]、CSDM方法(coherent switching with decay of mixing method)[14]以及最近提出的量子路径方法[15]等.这些方法已被成功应用于分子动力学[16−20]以及电荷传输研究[21].除以上混合模拟方法外,含时量子波包方法[22−24]也被广泛应用于三原子分子系统的分子动力学模拟[25−28].

本文对最近提出的量子路径方案做进一步研究.量子路径方案认为,由牛顿方程描述的核的经典运动对电子的量子运动起到了量子测量的作用,应当用量子测量理论给出描述[29].除了在几个典型的模型势能面系统中获得成功外,量子路径方案还被用于模拟有机分子N2CO的光分解动力学,获得了令人满意的结果[30].本文将进一步模拟检验量子路径方案在更多的模型系统中的相关结果,包括单交叉模型、双交叉模型、拓展耦合模型、哑铃模型以及双弓模型.由于难以在严格意义上得到退相干速率,我们特别模拟比较了从不同物理考虑得到的三个退相干速率公式,包括冻结高斯波包近似(frozen Gaussian approximation,FGA)[31]、能量分辨(energy discrimination,ED)[14,32]以及力分辨(force discrimination,FD)[15].发现对于结构较简单的势能面模型,三种退相干速率都能得到较好的结果.然而对于较复杂的势能面模型,由于复杂量子干涉的原因,与其他混合经典-量子动力学方案类似,量子路径方案仍然难以得到较准确的结果.

2 量子路径模拟方案

2.1 哈密顿量和量子路径方程

在包含所有电子和原子核的总哈密顿量中除去原子核的动能部分,可以得到电子的哈密顿量:

式中,第一项描述了电子的动能,其中mj为电子质量;第二项描述所有相互作用静电势能,其取决于量子部分电子坐标r≡{rj;j=1,2,···}及经典部分原子构型R.选择一组满足正交归一性和完备性的电子基函数ϕj(r,R)展开电子波函数ψ(r,R,t)=∑jcj(t)ϕj(r,R).通常此电子波函数的基函数选取电子哈密顿量Hel(r,R)的瞬时本征态 (只考虑非简并情况),即BO绝热波函数Hel(r,R)ϕj(r,R)=εj(R)ϕj(r,R), 其中,εj(R)代表第j个绝热电子态|ϕj(R)〉对应的势能面.

电子部分的动力学性质由薛定谔方程iħ˙ψ=Helψ确定. 我们定义电子哈密顿量矩阵元Vjk(R)=〈ϕj(r,R)|Hel(r,R)|ϕk(r,R)〉, 在绝热表象下方程的形式为

根据绝热电子态的正交性可证绝热耦合矢量具有反厄米性质:djk(R)=−d∗kj(R).与djk(R)决定了各BO势能面之间的非绝热耦合强度.当两个绝热电子态的能量差很大时,djk(R)可以忽略,则可以回到绝热近似下的在单一势能面上动力学.反之,则需要求解电子与原子核互相耦合的运动.

由于电子和原子核存在着耦合,电子和原子核的运动也是互相影响的.讨论电子态的动力学时,通常认为原子核对电子部分的影响在于电子态是原子核构型R的函数.如果从量子测量的观点研究非绝热分子动力学模拟问题,经典的原子运动也会导致电子部分的量子态产生退相干[32−36].随着量子态的不断演化,原子部分也将受到与量子态对应的经典力的影响.如果将此经典力视为一种可以获得电子态信息的“测量仪器”,则该仪器对电子部分的量子态进行有效的连续测量.例如,原子在不同的势能面上会感受到不同的经典力,相当于测量过程中获得了某种“结果”,从而将引起量子跳跃或量子叠加态的逐渐塌缩.这种连续获取信息的测量过程下的动力学演化,可以由量子路径方程描述如下[29]:

式中ρ是电子态密度矩阵,其对角元描述各个BO态的占据概率,非对角元描述它们之间的相干性.

方程(4)右端的第一项描述了电子态的相干动力学演化,第二项和第三项描述了“信息获取”(量子测量)的反作用.其中的Lindblad超算符定义为

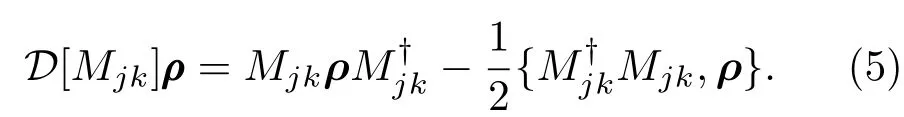
式 中, 测 量 算 符Mjk(R)=|ϕj(R)〉〈ϕj(R)|−|ϕk(R)〉〈ϕk(R)|, 是与态ϕj(R)和ϕk(R)相关的测量算符.Γjk描述了电子由于原子力和其他因素导致的测量过程中的退相干速率,γF,jk是根据原子力测量对信息的获取速率.在忽略其他环境影响下Γjk=γF,jk.描述 “信息获取”导致的反作用的另外一个超算符,定义为

2.2 退相干速率

方程(4)中的退相干速率,难以在严格意义上得到,但可以通过定性的物理分析得到有明确物理意义的一些结果.例如,利用FGA[37],Schwartz等[33,38]通过计算不同势能面上演化的冻结高斯波包之间的交叠,得到了如下的退相干速率公式:

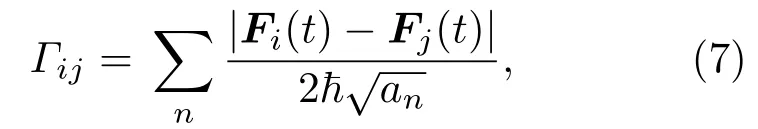
式中,an是核波函数的有效宽度,其大小为

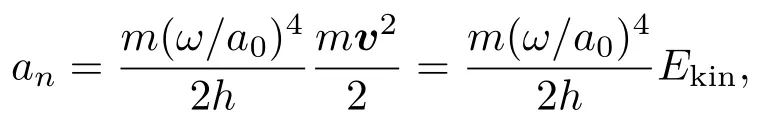
其中,ω是一个经验参数,a0是玻尔半径,Ekin是原子核的能量;Fi(j)(t)是ϕi(j)(R,r)态的Hellmann-Feynman力

进一步,Akimov等[31]对(7)式进行了简化,得到了更加简单和实用的退相干速率公式:

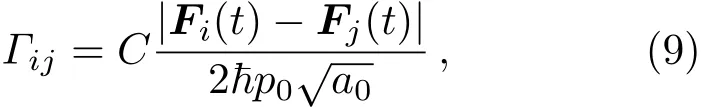
其中,p0是初始原子核动量大小,C是一个经验参数.

作为另外一种不同的方案,Truhlar等[14,32]根据“退相干时间应不小于最小的电子特征时间尺度”(基于能量-时间测不准关系的考虑),唯像地提出了一个ED退相干速率公式:

其中,Ekin是原子核的能量,C=0.1 Hartree是一个经验参数.值得注意的是,此退相干公式与原子核受力无关,在势能面平行区得到的退相干速率非零.

除了“ED”,原子在不同势能面上的经典运动,将感受到不同的“力”.基于对力的分辨,提出了力分辨(FD)退相干速率[15]:

式中,τc为核的特征运动时间,通常为电子运动特征时间的10−3倍;j(t)为原子处于势能面Vj(R)感受到的粗粒化平均力,其具体形式将在下节中详细讨论.

2.3 量子路径算法中原子核的受力形式

在混合经典-量子动力学中,原子核由牛顿运动方程确定经典运动规律.其中Erenfest平均场理论结合电子态演化的薛定谔方程,可以得到经典力:

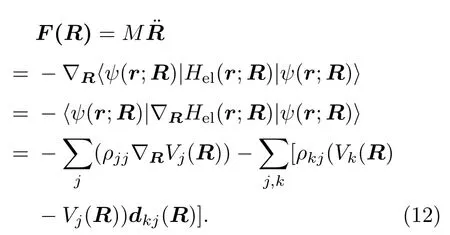
由于含时的|ψ(r;R)〉并不一定是电子哈密顿量的本征态,式中第三个等号成立并不是由Hellmann-Feynman定理直接求得的结果[39],而是与Erenfest平均场理论的演化方程(2)有关.此Erenfest力被许多势能面跳跃理论采用作为原子力.但电子演化过程中含有随机性质的势能跳跃,由于电子演化规律不遵循简单的薛定谔方程,原子受力仍采用如上的形式就不再合适.

在量子路径理论中,绝热表象下决定原子核运动的经典力为

此原子力由含有随机项的电子态演化方程(4)推导.此时原子力形式较为复杂,且其表达式中含有随机项.与我们将原子核受力作为对电子态的量子测量输出的观点十分吻合.表明在电子时间尺度观察原子,其感受到的 “瞬时力”同电子演化一样也含有随机性.(13)式中第二项Vj∇ρjj=Vj˙ρjj/˙R已经看出“原子瞬时力”包含了随机涨落成分.

由于原子运动相对电子运动比较缓慢,原子在t时刻受到特征时间τ内“粗粒化的平均力”¯Fj(t)作用,且此力不再包含随机性.此外,在量子理论中也可以将 “原子时间尺度 (τ)”内的平均势能变化率作为原子受力,其大小为

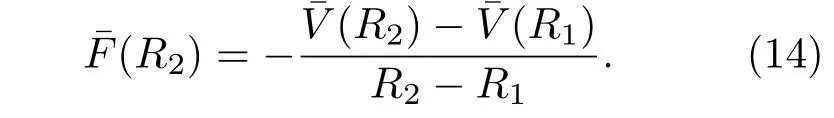
广泛被势能面跳跃方法采用的Erenfest力(12)式和平均势能变化确定的平均力(14)式,其区别不仅在于是否包含随机性.而且在转向点处可能会出现两种力的受力方向相反的矛盾(附录A).因此,在势能面跳跃方法中原子受力仍采用Erenfest受力是不适宜的.

2.4 关于能量守恒方案

在势能面跳跃理论中,由于原子核在不同势能面之间跳跃,原子核势能的变化并不连续.因此,在跳跃后调节原子核的运动速度以保证原子核的总能量守恒:

式中,dk采用有效平均场非绝热耦合矢量[33],

速度调节参数γ通过跳跃前后的动能差等于负的势能差确定.如果发生原子核跳跃至某势能面,而且此势能面能量高于原子核初始总能量的情况,则认为此次跳跃是“禁闭”的.此外,根据经典力学理论,此点是原子核的“反向点”应将原子核的动量转向,同时保持电子部分的量子态不变[40].

与势能面跳跃理论不同,量子路径理论中原子核的势能变化是连续的.在理论上,采用(13)式或在dt→0时本质上与其一致的(14)式作为原子力,可以保证能量自动守恒.但由于实际计算时采用的时间步长dt/=0,导致演化中每一步的能量计算误差均为正数,即能量 “正误差”(详见附录B).因此我们针对量子路径理论设计以下方案处理能量守恒问题.

第一,在模拟过程中,始终确保原子势能小于系统的初始时刻的总能量即V(R)=Tr[Hel(R)ρ(R)]＜E0,E0可以定义为演化初始时刻的能量,倘若原子处于某一个单势能面Vj(R),同样要求Vj(R)≤E0.

第二,对于满足V(R1)=E0的位置R1,由于其动能为0无法继续向前运动,因此需重新定置R2,但新平均势能VM(R2)=E0仍成立,方法如下:首先确保R2与R1有相同的电子波函数;再去掉最低势能面的分量;最后重新归一化波函数计算新的平均势能VM(R2).

第三,从R2处开始新的演化模拟,且保持电子部分不会发生任何改变,但原子的动能会改变为E0−V(R2),其动量的方向与原来动量方向相反(即反射).

第四,在非转折点,设定能量误差上限δ,当某时刻原子核总能量与初始总能量之间的差值大于δ时,则保持电子态不变并重新调整动量使原子核总能量满足能量守恒.

其中,在反向点处的处理方法与文献[12]处理方式以及Subotnik[41]提出的能量守恒方法有类似之处.

2.5 量子路径算法的实施步骤

量子路径方案不仅在理论概念上有清晰的物理意义,同时也是一种容易实现的分子动力学模拟算法.与Tully等[9]的势能面跳跃算法相比,该方案并不需要人为设计复杂的算法使系统“跳跃”到某个势能面上.现将量子路径方案的算法概述如下.

1)将每一条轨迹中原子核的位置、动量以及电子密度矩阵初始化.

2)计算t时刻核构型R(t)所对应的哈密顿量(1)式的本征值和本征矢,得到绝热基态.每隔一个 “原子时间尺度 (τ=1000dt)”,计算原子的受力:.在同一个原子时间尺度τ内,原子核的速度保持不变,在t+τ时刻,原子核的速度变为(t+τ)=˙(t)+(t)τ.

3)每经过“电子时间尺度”dt,选取合适的测量速率形式,计算Wiener增量ΔWjk=ξjk(t)dt.并求解相应的量子路径方程(4)式.

4)在同一个原子时间尺度τ内,原子核的速度保持不变,原子核的位置为R(t+dt)=R(t)+(t)dt.如果在t时刻,将进入下一个τ时段,则从t到t+τ时段内速度为˙(t+τ)=˙(t)+(t)τ.

5)查看系统总能量,如果不需要进行动量调整则返回第二步继续计算.如需要则按照上节的讨论进行调节.

3 对若干模型的数值模拟

本节分别使用FGA,ED和FD得到的退相干速率公式,利用量子路径方案模拟五个模型,包括三个 Tully模型[9]和Subotnikhe和Shenvi[42]提出的另外两个模型,并与严格的量子动力学结果做比较.对每一个模型,我们都将平均2000条随机量子路径.对于每条路径,粒子都从势能面的左端出发,向右演化.原子质量设为M=2000 a.u..

3.1 单交叉模型

在非绝热表象中,该模型势能面为[9]

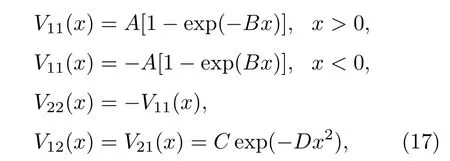
其中,A=0.01,B=1.6,C=0.005,D=1.0.该模型的绝热势能面和耦合强度如图1(a)所示,模拟结果见图1(b)—(d).可以看出,有3个特殊的动量区域值得讨论.第一,动量k＜4.5时,经典的粒子几乎全部返回到低势能面上,这主要是因为经典粒子的动能较小,无法提供其克服势垒继续向前演化的能量.第二,动量5＜k＜10时,处于低势能面的粒子会隧穿势垒继续沿原方向演化,造成隧穿低势能概率在k≈5时有较大幅度的梯度增加(图1(b)所示);动量5＜k＜8时粒子动能较小无法跃迁到高势能面上,所以反射概率为0;动量k≈8时,反射到低势能面的概率略有增加(图1(c)所示),因为在8＜k＜10时,粒子有足够的动能向高势能跃迁,但无足够的动能使其隧穿高势能面的势阱,所以会以一定概率返回到低势能面上.第三,动量k＞10时,在耦合区域低势能面的粒子以一定的概率跃迁到高势能面并沿原方向继续演化.

图1 (网刊彩色)单交叉模型 (a)绝热势能(实线)和非绝热耦合强度(虚线)随原子位置坐标x的变化;(b),(c),(d)分别为隧穿至低势能面、反射至低势能面和隧穿至高势能面的概率随初始动量k的变化;利用FD退相干速率(蓝色方块)、ED退相干速率(绿色三角形)以及FGA退相干速率(红色空心圆)通过量子路径理论进行模拟,并与全量子动力学(Exact)(黑色实心点)模拟做了对比Fig.1. (color online)Single avoided crossing model:(a)Adiabatic potential energy level(solid line)and nonadiabatic coupling strength(dashed line)as a function of position x;panels(b),(c)and(d)are,respectively,initial momentum k effects on probabilities of transmission to the lower energy surface,ref l ection to the lower energy surface,and transmission to the upper energy surface.We present the quantum trajectory results by using the FD(blue square),ED(green triangle)and FGA(open red circles)decoherence rates,and compare them with the exact result from full quantum dynamics(Exact)simulation(black solid circle).

通过对三种退相干速率模拟的结果的比较,发现它们与全量子动力学的模拟结果几乎相同.在几个特殊动量区域也都符合,尤其是使用FD退相干速率和FGA退相干速率,与全量子动力学的模拟结果完全吻合.

3.2 双交叉模型

双交叉模型将导致量子干涉,并将造成隧穿概率的Stueckelberg振荡,所以该模型更具挑战性.该模型势能面为[9]

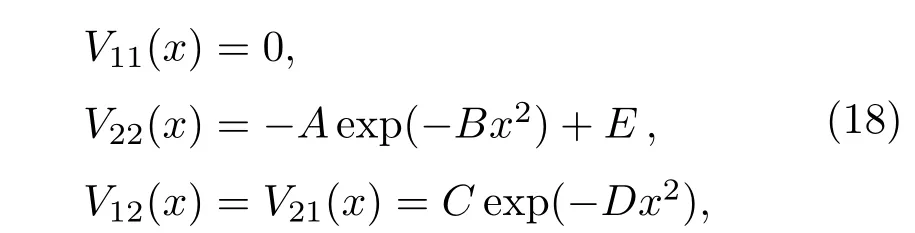
其中,A=0.10,B=0.28,C=0.015,D=0.06和E=0.05.从图2(a)可以看出,此模型由一个直线和两个反转的高斯曲线组成,并且有两个连续的强耦合区.

粒子从左端较低的势能面开始,向右演化.当进入第一强耦合区可能发生电子态的跳跃,使粒子离开第一强耦合区域时会以一定的概率继续沿低势能面向前演化,或发生量子跳跃以一定概率沿高势能面向前演化,亦或以一定概率返回高低势能面.若从波包演化的角度分析,在此演化过程中可能发生波包的分离与相遇.据图2(b)—(d)全量子动力学的模拟结果显示:当粒子初始动能较低(lnE＜−3)时,绝大多数粒子会继续沿低势能面向前演化,少数部分粒子会返回到低势能面.造成此现象的主要原因是在第一个耦合区部分粒子会向高势能面跃迁.但是,处于高势能面的粒子势能增加,由于动能较低,无法使其隧穿继续向前演化.当粒子初始动能较大(lnE＞−3),粒子会隧穿到低势能面或高势能面上继续向前演化.高低势能面波包在第二耦合区会发生相干叠加,从而造成振荡现象.随着初始动能的增加,高低势能面波包演化速率差也会较小,促使振荡振幅变大.

图2 (网刊彩色)双交叉模型 (a)绝热势能(实线)和非绝热耦合强度(虚线)随原子位置坐标x的变化;(b),(c),(d)分别为隧穿至低势能面、反射至低势能面和隧穿至高势能面的概率随初始能量E的变化;利用FD退相干速率(蓝色方块)、ED退相干速率(绿色三角形)以及FGA退相干速率(红色空心圆)通过量子路径理论进行模拟,并与全量子动力学(Exact)(黑色实心点)模拟做了对比Fig.2.(color online)Dual avoided crossing model:(a)Adiabatic potential energy(solid lines)and nonadiabatic coupling strength(dashed line)as a function of position x;panels(b),(c)and(d)are,respectively,initial energy E effects on probabilities of transmission to the lower energy surface,ref l ection to the lower energy surface,and transmission to the upper energy surface.We present the quantum trajectory results by using the FD(blue square),ED(green triangle)and FGA(open red circles)decoherence rates,and compare them with the exact result from full quantum(Exact)dynamics simulation(black solid circle).

对三种退相干速率模拟结果比较发现,利用FD和FGA退相干速率模拟的数值结果与全量子动力学模拟结果符合良好.然而利用ED退相干速率进行的模拟在高动能区域无振荡现象产生;在低初始动能区域也过高估测了返回的概率(大约高一个量级),与全量子动力学结果相差较大.

3.3 扩展耦合模型

扩展耦合模型是一个非常重要的模型,其势能面形式为[9]

其中的系数选取为A=6×10−4,B=0.1和C=0.9.相应的绝热势能面如图3(a)所示,可以发现在此模型中包含了一个很宽的耦合区.

当粒子以低动量从低势能面开始演化时,在强耦合区变为混合叠加态,但由于能量守恒,处在高势能面的波包由于动能无法提供其继续沿原方向演化的能量,可能造成高势能面的波包返回,但低势能面的波包可以继续向前演化,造成波包演化的退相干.

从图3(b)—(d)可以看出:当初始动量k＜28时,处在高势能面的波包返回,而处在低势能面的波包继续隧穿,利用FD退相干速率与FGA退相干速率模拟的演化结果与全量子动力学模拟结果几乎一致,然而利用ED退相干速率模拟的结果与全量子模拟结果差异较大,原因是过高地估计了返回到高低势能面的概率;对于初始动量k＞28,处在高势能面的粒子有足够能量使其向前演化,所以在此动量区,利用三种速率公式模拟的结果几乎与全量子结果相似.

图3 (网刊彩色)扩展耦合模型 (a)绝热势能(实线)和非绝热耦合强度(虚线)随原子位置坐标x的变化;(b),(c)和(d)分别为隧穿至低势能面、反射至低势能面和反射至高势能面的概率随初始动量k的变化;FD退相干速率(蓝色方块)、ED退相干速率(绿色三角形)以及FGA退相干速率(红色空心圆)通过量子路径理论进行模拟,并与全量子动力学(Exact)(黑色实心点)模拟做了对比Fig.3.(color online)Dual avoided crossing model:(a)Adiabatic potential energy(solid lines)and nonadiabatic coupling strength(dashed line)as a function of position x;panels(b),(c)and(d)are,respectively,initial momentum k effects on probabilities of transmission to the lower energy surface,ref l ection to the lower energy surface,and ref l ection to the upper energy surface.We present the quantum trajectory results by using the FD(blue square),ED(green triangle)and FGA(open red circles)decoherence rates,and compare them with the exact result from full quantum(Exact)dynamics simulation(black solid circle).

3.4 哑铃模型

哑铃模型是一个对称拓展耦合模型,其形状类似于哑铃.其势能面和耦合强度,在x轴大于零部分(反应结束部分)与扩展耦合模型的形状一致,在x轴小于零部分(反应开始阶段)相当于反转的扩展耦合模型.其势能面为[42]

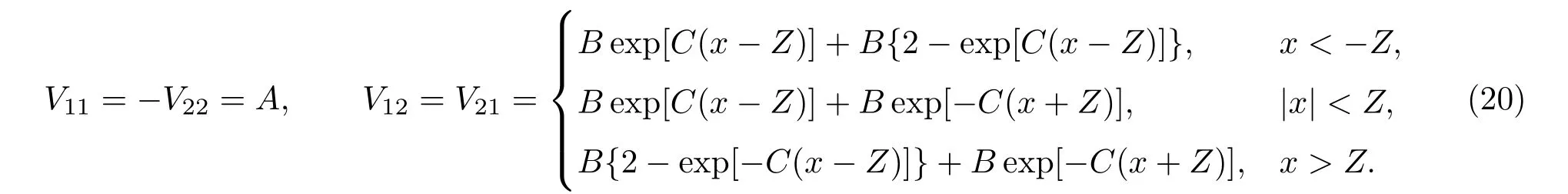
A,B和C系数选取与模型(19)一致,Z=10.从图4(a)可以看出,绝热势能面上有两个强耦合区.

在图4(b)—(d)中,从全量子动力学演化结果可以看出:首先,在初始动量k＜28时,原子无法隧穿,几乎全部反射到低势能面上;其次,当32＜k＜40时,部分原子隧穿至低势面,部分反射到低势能面,从波包演化的角度分析,当初始动量在此间隔时,原子可以隧穿障碍到达高势能面和低势能面,但隧穿到高势能面的原子在演化过程中势能会不断地增加,根据能量守恒,其无法提供继续向前演化的动能,隧穿到高势能面的原子会反射到低势能面上;最后,当k＞40时,原子完全隧穿至低势能面或高势能面上.

比较发现,利用FGA退相干速率和FD退相干速率,通过量子路径方法可以准确地模拟系统的演化,尤其利用FGA退相干速率 (常数C=1.0)可以得到与全量子动力学模拟几乎完全吻合的结果.但在初始动量32＜k＜40时,利用ED退相干速率模拟得到的结果与全量子动力学结果相差略大.

图4 (网刊彩色)哑铃模型 (a)绝热势能(实线)和非绝热耦合强度(虚线)随原子位置坐标x的变化;(b),(c),(d)为隧穿、反射的概率随初始动量k的变化(与图3类似);利用ED退相干速率 (绿色虚线)、FD退相干速率(蓝色实线)以及FGA退相干速率(红色点划线)分别通过量子路径理论进行模拟,并与精确的量子动力学(Exact)(黑色虚线)模拟做了对比Fig.4.(color online)Dumbbell potential model:(a)Adiabatic potential energy(solid lines)and nonadiabatic coupling strength(dash line)as a function of position x;panels(b),(c)and(d)stand for initial momentum k effects on transmission and ref l ection probabilities as described in Fig.3.The quantum trajectory results by using FD(blue solid lines),ED(green dashed lines)and FGA(red chain line)decoherence rates are compared with the exact one from the full quantum(Exact)dynamics simulation(black dashed lines).

图5 (网刊彩色)双弓模型 (a)绝热势能(实线)和非绝热耦合强度(虚线)随原子位置坐标x的变化;(b),(c),(d)为隧穿、反射的概率随初始动量k的变化(与图3类似);利用ED退相干速率(绿色虚线)、FD退相干速率(蓝色实线)以及FGA退相干速率(红色点划线)分别通过量子路径理论进行模拟,并与精确的量子动力学(Exact)(黑色虚线)模拟做了对比Fig.5.(color online)Double arch geometry:(a)Adiabatic potential energy(solid lines)and nonadiabatic coupling strength(dash line)as a function of position x;panels(b),(c)and(d)stand for initial momentum k effect on transmission and ref l ection probabilities as described in Fig.3.The quantum trajectory results by using FD(blue solid lines),ED(green dashed lines)and FGA(red chain line)decoherence rates are compared with the exact one from the full quantum(Exact)dynamics simulation(black dashed lines).

3.5 双弓模型

双弓模型在开始和反应结束时,两个势能面基本重合,形式为[42]

A,B,C系数选取与模型(19)一致,Z=4.从图5(a)可看出,该模型的非绝热势能面形状像两个弓.基于全量子动力学结果,此模型中有三个特殊的动能区域.第一,在低能量区域(k＜28),如图5所示,仅仅只有处于低势能面的波包进行了隧穿,而处于高势能面的波包由于动能无法提供其继续向前演化能量而被返回.造成其退相干率为100%.第二,在中能量区域(k刚大于28),波包可以隧穿到高势能面或者低势能面.然而低势能面的波包由于能量守恒具有较大的速度,造成高低势能面的波包在第二个非绝热耦合区之前发生分离,所以势能面的占据概率出现部分振荡的现象.第三,在高能量区域(k≫28),由于弓形势垒所造成的速度差相对较小,上能级和下能级的波包发生了干涉现象,在此动量区域发现有较强的振荡.

我们的模拟结果显示:在初始具有较大动量时,利用FD退相干速率与ED退相干速率进行的模拟,最终两个势能面的占据概率几乎是一致的,与全量子模拟的振荡结果差别略大.利用FGA退相干速率的模拟结果,虽然在隧穿部分也有振荡现象,但其振幅随着初始动量的增加变化缓慢,与全量子动力学模拟也不完全符合.在初始动量较低时,利用三种速率公式模拟也都无法得到满意的结果.原因是在“混合量子-经典”方法中,核的运动由牛顿方程描述,难以对有复杂量子干涉现象的系统给出较理想的结果.

4 总 结

基于近期发展的经典-量子混合模拟非绝热分子动力学的量子路径方法,本文对5个典型势能面模型进行了模拟,包括单交叉模型、双交叉模型、拓展耦合模型、哑铃模型以及双弓模型.在模拟过程中,我们对比检验了3个不同的退相干速率公式,分别为FGA,ED以及FD退相干速率.比较发现,在单交叉模型中,三种退相干速率的模拟效果几乎一致,均与全量子结果符合良好.对于双交叉模型、拓展模型以及哑铃模型,利用FGA与FD退相干速率,模拟的结果更好 (优于ED退相干速率).在双弓模型中,发现使用三种退相干速率,模拟结果与精确值差别较大,都不能很好地模拟精确的量子动力学过程.原因是“混合量子-经典”方法中,核的运动由牛顿方程描述,难以纳入复杂的量子干涉因素.如何发展更加有效的混合经典-量子模拟方案,是未来研究的重要课题.

附录A 瞬时力与Erenfest力“反向”问题

以一维势能V1=−V2的Tully模型[9]一为例.在非耦合区,定义V1为上能级势能面,若粒子从位置R1点向R2点演化,通过平均势能面梯度得到力的大小:

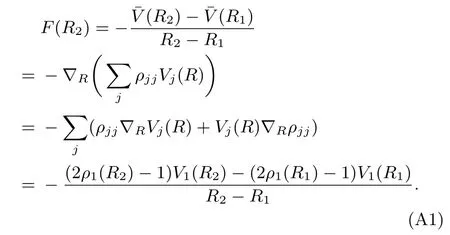
在任一R点处,其 Erenfest力大小则为(第二个等号是考虑非耦合区,dji(R)近似为零的特例)

若从R1点演化到R2,电子态的密度矩阵不发生变化,二力可以近似相同.但考虑电子态由于测量投影可以发生如下变化:∇V1始终是正值,在位置R1,R2处,粒子所处上能级概率分别为ρ1(R1),ρ1(R2),并且(2ρ1(R2)−1)V1(R2)−(2ρ1(R1)−1)V1(R1)＜0,2ρ1(R2)−1＞0.则

原子感受到的平均势能面确实下降,所以根据 “平均势能的变化率”确定的力是正方向.但是,由于基本可以认为原子处于上势能面,Erenfest力应该是负方向.其原因在于量子路径方法模拟过程中的∑jVj∇Rρjj/= ∑j,kρkj(Vk−Vj)dkj,即Erenfest力不能描述电子态占据概率变化产生的力对系统势能的改变.并且Vj∇Rρjj=Vj˙ρjj/˙R,在速度较低的情况,势能梯度产生的力−∑j(ρjj∇RVj)小于电子态变化产生的力−∑j(Vj∇Rρjj),在此情况下的Erenfest力忽略了起主导作用的电子态变化产生的力,导致了上述问题.

附录B 借瞬时力(14)式实现能量守恒的误差分析

采用新的原子受力的表达式,理论上可以自动实现能量守恒.在一维模型中,原子从t时刻,经历时间间隔Δt的过程中,速度保持不变,新的位置

t+Δt时刻的速度

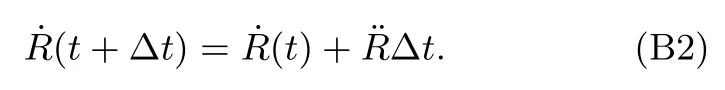
定义时间间隔Δt内的“平均加速度”

则容易推出t+Δt时刻的能量

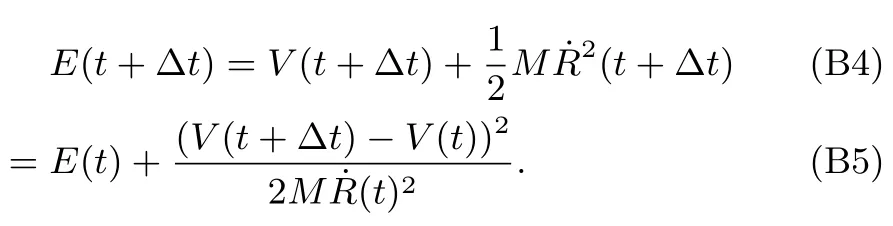
在小量可以忽略的情况下,能量自动守恒

如果原子的初始动量较小,原子在跳跃至高势能面后要转向,发生“反射”现象.此时,原子速度要减小至接近0,然后转向.在速度接近于0的过程中,(B6)式中的分母较小,因此能量中的增量仍可能具有一定的数值.并且1)即使这个增量较小,但由于是累加,因此总能量只会上升,无法减小;2)离开了耦合区后,只要投影没有完毕,此增量就一直在累加,因此,总能量在实际计算时会有一定的能量增量误差.

图B1 (网刊彩色)通过量子路径方法,分别模拟了使用能量守恒(CE)方案(绿色实线)以及未使用能量守恒(NCE)方案(蓝色虚线)两种情况总能量随时间的变化Fig.B1.(color online)Energy variations along the time.The results obtained by using(blue dashed lines)and not-using(green solid lines)the rule of energy conservation.为了更清楚地反映此现象,我们以拓展耦合模型为例,用量子路径方法模拟了单条路径总能量随演化时间的变化(图B1).设置初始动量k0=8.1578 a.u.(有反射现象产生).从图B1我们发现其模拟结果与以上理论分析完全吻合.

[1]Gerber R B,Buch V,Ratner M A 1982J.Chem.Phys.77 3022

[2]Micha D A 1983J.Chem.Phys.78 7138

[3]Li X S,Tully J C,Schlegel H B,Frisch M J 2005J.Chem.Phys.123 084106

[4]Tully J C,Preston P K 1971J.Chem.Phys.55 562

[5]Miller W H,George T F 1972J.Chem.Phys.56 5637

[6]Kuntz P J,Kendrick J,Whitton W N 1979Chem.Phys.38 147

[7]Blais N C,Truhlar D G 1983J.Chem.Phys.79 1334

[8]Ali D P,Miller W H 1983J.Chem.Phys.78 6640

[9]Tully J C 1990J.Chem.Phys.93 1061

[10]Kuntz P J 1991J.Chem.Phys.95 141

[11]Webster F,Wang E T,Rossky P J,Friesner R A 1994J.Chem.Phys.100 4835

[12]Prezhdo O V,Rossky P J 1997J.Chem.Phys.107 825

[13]Zhu C Y,Jasper A W,Truhlar D G 2004J.Chem.Phys.120 5543

[14]Zhu C Y,Nangia S,Jasper A W,Truhlar D G 2004J.Chem.Phys.121 7658

[15]Feng W,Xu L T,Li X Q,Fang W H,Yan Y J 2014AIP Adv.4 077131

[16]Li B,Han K L 2009J.Phys.Chem.A113 10189

[17]Li B,Chu T S,Han K L 2010J.Comput.Chem.31 362

[18]Yang M H,Huo C Y,Li A Y,Lei Y B,Yu L,Zhu C Y 2017Phys.Chem.Chem.Phys.19 12185

[19]Lu J F,Zhou Z N 2016J.Chem.Phys.145 124109

[20]Schubert A,Falvo C,Meier C 2016J.Chem.Phys.145 054108

[21]Wang L J,Prezhdo O V,Beljonne D 2015Phys.Chem.Chem.Phys.17 12395

[22]KosloffR 1988J.Phys.Chem.92 2087

[23]Schatz G C 1996J.Phys.Chem.100 12839

[24]Zhang J Z H,Dai J,Zhu W 1997J.Phys.Chem.A101 2746

[25]Guo H,Yarkony D R 2016Phys.Chem.Chem.Phys.18 26335

[26]Chu T S,Zhang Y,Han K L 2006Int.Rev.Phys.Chem.25 201

[27]Chu T S,Han K L 2008Phys.Chem.Chem.Phys.10 2431

[28]Zhang S B,Wu Y,Wang J G 2016J.Chem.Phys.145 224306

[29]Jacobs K,Steck D A 2006Contemp.Phys.47 279

[30]Xie B B,Liu L H,Cui G L,Fang W H,Cao J,Feng W,Li X Q 2015J.Chem.Phys.143 194107

[31]Akimov A V,Long R,Prezhdo O V 2014J.Chem.Phys.140 194107

[32]Zhu C Y,Jasper A W,Truhlar D G 2005J.Chem.Theory Comput.1 527

[33]Bedard-Hearn M J,Larsen R E,Schwartz B J 2005J.Chem.Phys.123 234106

[34]Prezhdo O V 1999J.Chem.Phys.111 8366

[35]Granucci G,Persico M 2007J.Chem.Phys.126 134114

[36]Thachuk M,Ivanov M Y,Wardlaw D M 1998J.Chem.Phys.109 5747

[37]Heller E J 1981J.Chem.Phys.75 2923

[38]Schwartz B J,Bittner E R,Prezhdo O V,Rossky P J 1996J.Chem.Phys.104 5942

[39]Lan Z G,Shao J S 2012Prog.Chem.24 1105(in Chinese)[兰峥岗,邵久书2012化学进展 24 1105]

[40]Hammes-Schiffer S,Tully J C 1994J.Chem.Phys.101 4657

[41]Subotnik J E 2010J.Chem.Phys.132 134112

[42]Subotnik J E,Shenvi N 2011J.Chem.Phys.134 024105