基于模拟退火算法的日照约束条件下高层建筑优化设计

党向盈，姜代红，黄小林

(徐州工程学院 江苏省智慧工业控制技术重点建设实验室，江苏 徐州 221000)



基于模拟退火算法的日照约束条件下高层建筑优化设计

党向盈，姜代红，黄小林

(徐州工程学院 江苏省智慧工业控制技术重点建设实验室，江苏 徐州 221000)

提出一种基于模拟退火算法的高层建筑高度优化求解的方法.首先，将拟建建筑用地均匀分为若干小格，将这些小格向上拉伸为小柱，基于小柱与被遮挡窗口的位置关系，确定窗口累计日照时间；然后，基于窗口最小日照时间的约束，构建拟建建筑高度最大值的数学模型；最后，基于该数学模型，采用模拟退火算法求解拟建建筑最优高度.实验结果表明，本文方法的数学模型合理，能够准确获得被遮挡窗口的日照累计时间，并在该日照约束条件下，通过退火方式的多次扰动，快速求解拟建建筑高度的最优值.因此所提方法为建筑结构优化设计提供一种有效途径.

日照约束;模拟退火算法;容积率；优化设计

随着中国城市建设的快速发展，高层建筑楼群密度不断提高，对原有房屋日照的遮挡也越来越严重，从而造成了高层建筑与日照环境质量之间的矛盾日益尖锐[1-2].对拟建建筑的建设规划时，对建筑的设计，传统方法主要依据《城市规划设计规范》等要求，但是，如果对日照要求严格的地区，进行精确分析和规划设计，只根据一般的日照标准，传统方法就显得过于粗略和简单.鉴于此，很多学者对建筑优化设计提出很多解决方法[3-4],尤其采用进化算法对建筑组合优化设计[5-12]的研究比较广泛.

容积率是指一个小区的总建筑面积与用地面积的比率，该指标直接反映土地利用率.由于城市资源严重短缺，容积率受到周边建筑环境、日照、通风等因素的限制.如何有效地提高土地的利用率，是迫切解决的问题.成三彬[11]采用遗传算法与日照相结合，求解拟建建筑的最大容积率，取代了传统凭借经验的方式计算最大容积率的方法，在实践中取得了良好的效果.因此，本文解决的主要问题是采用合适的方法求解拟建建筑最大容积率，考虑到拟建建筑的规划用地面积是已知的，因此，本文研究最大容积率的求解，实质等价于拟建建筑最优高度的求解.

模拟退火(simulatedannealingalgorithm,SA)[13]是根据熔融金属中粒子的统计力学提出来的，其与组合最优化问题的求解过程非常相似，因此，本文考虑采用模拟退火算法求解拟建建筑高度最优值.而且，本文建立的数学模型和求解方法，与以往文献也不完全相同.所提方法，首先，基于被遮挡窗口日照分析，确定窗口累计日照时间；然后，基于窗口日照约束，构建拟建建筑高度最大值的数学模型；最后，基于该数学模型，采用模拟退火算法进行求解.

1 基于被遮挡窗口与拟建建筑位置关系的窗口日照分析

1.1 确定日照参数

对拟建建筑优化设计时，拟建建筑基地面积、经纬度以及周边情况是已知的.为了进行日照分析，需要记录一些参数，计算地点的经度J，纬度χ，观测时间为Year、Month、Data、Hour、Minute，由此确定太阳位置.太阳的相关参数可以查找《地年气象观测规范》，进行计算.

1.2 确定被遮挡窗口

一般情况，位于拟建建筑南面建筑物，会对拟建建筑形成遮挡.以任意一个被遮挡窗口，作为一个拟观测顶点，把太阳的运动轨迹当作底面，这样就形成了一个日照圆锥.当拟建建筑物突出圆锥面的时候，就对观测点形成了遮挡，此时建筑物和圆锥面形成相贯线；同时作相贯线的切线，该切线对应一个太阳方位角[11].下面阐述基于太阳相关参数求解被遮挡窗口的过程.

已知拟建建筑区域的基底，将拟建建筑基底分成若干宽度为w的小格，将这些小格向上拉伸为若干小柱.被遮挡建筑的遮挡情况受拟建建筑东西方向的长度L，以及拟建区域最北侧的一排小柱影响，记这些小柱为h0,h1,…,hi,…hn-1，其中n=L/w为小柱的个数.

如图1所示为正南朝向被遮挡面的矩形与日照圆锥切面相交的一般情况，图中X1和X2之前的距离为遮挡区域.图2为小柱与被遮挡窗口距离关系,设第tsu时刻所形成的太阳时角为фsu，此时根据第h0个柱体位置，计算被遮挡区域的起始位置为X1=btgфsu；设第tss时刻所形成的太阳时角为фss，此时根据第hn-1个柱体，计算被遮挡区域的终止位置X2=L-btgфss；设窗口宽度为Wa，窗口间距为Wb，因此被遮挡建筑的控制窗口个数

(1)

1.3 确定被遮挡窗口日照累计时间

为了确定窗口日照累计时间，首先，以窗口中点为测试参照点，基于计算日期的有效日照时段，按照指定间隔分割时间切片；然后，根据不同时间切片内太阳位置，得到小柱的棒影长度矩阵；最后，考察小柱到窗口的距离向量与棒影长度矩阵的关系，获得窗口累计日照时间.

1)时间切片的确定

设一天的日出到日落的时间段为有效日照时间[tsu～tss]，被遮挡窗口获得最小连续日照时间为tm，以分钟为计算单位.分割的时间为St=(tss-tsu/tm)个，分别记为t0,…,tj,…,tst-1.

2)生成小柱棒影长度矩阵

图1 遮挡面与日照圆锥切面相交情况Fig.1 Intersection situation between covered surface and sunlight conic section

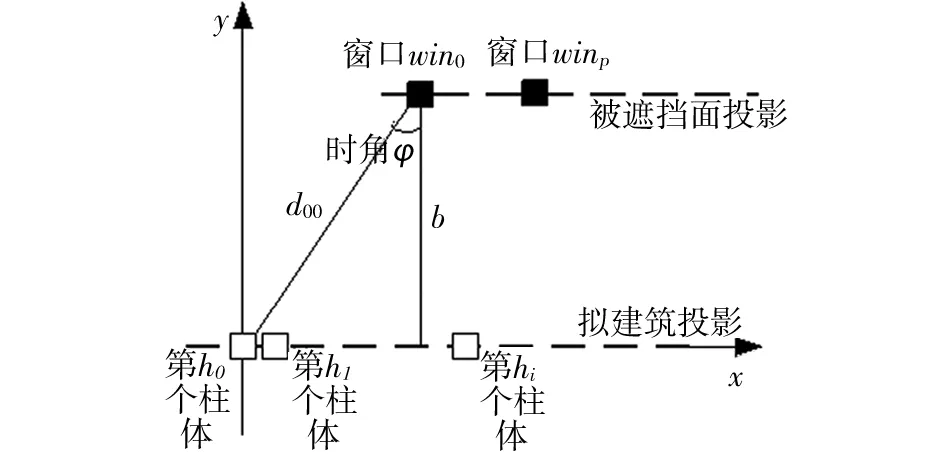
图2 小柱与被遮挡窗口距离关系示意Fig.2 Diagram of distance between column and covered window

采用传统棒影法[11]，计算小柱棒影长度.设直棒高度为H，此时太阳高度角α，则棒影长度l为

l=Hcotα.

(2)

为了构建小柱棒影长度矩阵，首先计算第hi个小柱tj时刻太阳的高度角，然后基于该高度角，由式(2)计算小柱hi在tj时棒影的长度lij.同理，可以得到n个小柱在时间t0,…,tj,…,tst-1的棒影长度，并构建小柱棒影长度矩阵为

3)生成小柱到窗口距离矩阵

已知拟建建筑与被遮挡建筑之间的间距为b，如图2所示，基于太阳时角φ，可以计算第h0个柱体与窗口win0之间的距离为d00

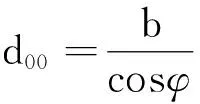
(3)

继续计算柱体与窗口之间的距离.因为小柱之间的距离相差ω，则第h1小柱体与窗口win0之间的距离为

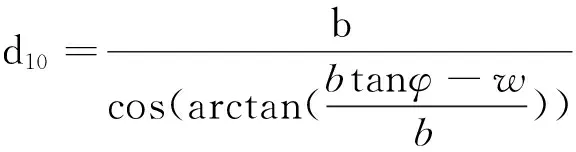
(4)

以此类推，可以计算第hi个柱体与窗口winp之间的距离dip；构建n个小柱分别到m个窗体的距离的矩阵为

4)确定窗口日照累积时间

基于矩阵Λ和矩阵L，考察小柱棒影长度lij与Dp的关系.如果满足Dp>lij，时间tj时，窗口winp可以获得最小连续日照时间tm，反之窗口winp获得最小连续日照时间为0.因此，记窗口winp在时间tj时获得的日照时间为Tpj，可以表示为

(5)

此外，需要考虑小柱宽度对Tpj的影响.由于窗体宽度Wa与小柱宽度w的之间存在比例关系R=Wa/w；根据日照平行光原理，单个小柱对于窗口的光照时间可以表示为tm×R；然而，满足向量Dp>lij条件的元素可能会存在多个，记为M(≥0)个.又因为存在tm时间长度的约束，所以，对于窗口winp最大日照时间不能超过tm，因此式(5)可以改进为

(6)

最后，考察在所有时间t0,…,tj,…,tst-1时，winp获得连续累计日照时间为

(7)

2 日照约束条件下拟建建筑高度的数学模型

已知《城市规划设计规范》要求的窗口日照时间不得少于Twin.很明显，当小柱高度H越高，窗口获得的日照时间就越短，反之，窗口获得的日照时间就越长，这显然是个组合优化问题.当所有窗口都满足规范的要求时间Twin时，此时的小柱高度H为最优值.

设窗口winp日照时间为Tsump，当Tsump≥Twin时，此时拟建建筑的高度H满足的函数，记为

fp(H)=Tsump.

(8)

类似的，窗口win0,…,winp,…,winm-1满足日照要求时，对应的目标函数分别记为f0(H),…,fp(H),…,fm-1(H).

很明显，当小柱高度H越高，窗口获得的日照时间就越短，当所有窗口都满足规范的要求时间Twin时，此时的小柱高度H为最大值，这显然是个组合优化问题，所以，可以将求解m个窗口获得规范的日照约束问题，转化为多目标求解最小值问题.

为此，建立的数学模型如下：

(9)

由式(9)可以看出，如果存在H，使得f0(H),…,fp(H),…,fm-1(H)同时满足最小值，则H为最优解.

3 基于模拟退火算法拟建建筑最佳高度的求解

针对式(9)数学模型，采用模拟退火算法进行优化求解.如图3所示为本文模拟退火算法求解流程，具体求解步骤如下.

Step1：参数的设置，在取值范围内，随机产生小柱的初始高度H，并采用实数编码；在区间[1,5]随机产生模拟退火算法的初始温度h，h即为模拟退火算法给定初始温度；

Step2：计算目标函数值f0(H+h),…,fp(H+h),…,fm-1(H+h)；

Step3：判断是否f0(H+h)>Twin,…,fp(H+h)>Twin,…,fm-1(H+h)>Twin；如果m个函数的值都不满足条件，将H+h赋值H，即H=H+h；然后转Step2；如果存在m′(

(10)

Step4：对于m′个函数，此时h过大，需要采取退火降温方式，设此时迭代次数为t，小柱的递增高度为h(t),

(11)

由式(11)曲线可知，温度h(t)的值随着迭代次数，缓慢减少.

Step5：判断是否h(t)-h(t-1)≤Δh，如果不满足条件，则将h(t)赋值h，即h=h(t)；转Step2；如果满足条件，停止进化，拟建筑高度达到最优值，输出结果.

需要说明的是，在Step3中，删除m-m′个不满足条件的函数，目的是为了减少目标函数的个数，降低了数学模型的求解难度.Δh取值一般很小，如0.1.

图3 本文模拟退火算法求解流程Fig.3 Flow chart of simulated annealing algorithm

4 实验结果与分析

测试地点：徐州市，经度J=117°11，纬度χ=34°15，计算时间2015年12月22日，有效日照时段为(08:00～16:00).设最小连续日照时间tm为10 min，则划分的时间为48个.由48个时间计算的太阳时角、高度角、赤纬角、方位角,结果如表1第3～6列所列.

设被遮挡建筑的窗口宽度Wa为1.5 m，窗口间距Wb为1.5 m，与被遮挡建筑之间的间距b为40 m；设拟建建筑东西方向长度L为60 m，小柱宽度w为1 m，由1.2小节可知，拉伸的小柱个数n为60个.根据规范要求，设窗口日照时间Twin为120 min.

表1 日照参数及棒影长度

表2 累计日照时间

采用模拟退火算法求解式(10)数学模型，得到拟建建筑高度最优值为27.14m，此时，所有窗体累计日照时间如表2所列，从表中可以看出，12个窗口获得累计日照时间均满足少于最小日照120min的《城市规划设计规范》要求，其中窗口1到8日照累计时间最小为130min，窗口11到12日照累计时间最多为190min.

进一步分析，当得到最佳小柱高度时，48个采样时间切片内小柱棒影长度的变化情况，如图4所示，其中x轴为时刻，y轴为棒影长度，具体小柱棒影长度值如表1第7和14列所示，从表中可以看出，在8:00时，棒影长度最大，为139.41 m；在12：00时，棒影长度最小，为37.69 m.

为了验证图4数值的合理性，拟建建筑最优值27.14时，以5号窗口为例，考察窗口到拟拟建建筑的距离和48个时间切片的棒影长度变化的关系，如图5所示，x轴为时间，y轴为棒影长度或窗口到拟建建筑的距离；灰色柱形序列为小柱的棒影长度；灰色线条为5号窗口与拟建建筑距离；图中标记“时间切片”表示在该时间棒影的长度，标记“5号窗口”表示5号窗口到拟建建筑的距离.从图5中可以看出，在第19个时间，“时间切片”为40.39， “5号窗口”为40.41，即此时棒影的长度小于窗口到拟建建筑的距离，由式(5)可知，5号窗口在第19个时间切片获得时间tm=10 min.以此类推，从第20个到第31个时间切片，其他12个时间切片，棒影长度均小于窗口到拟建建筑距离，则每个时间切片均获得时间tm=10 min.又因为R为1，由式(6)可知，5号窗口可获得累计日照时间为13×tm×Rmin.

图4 棒影长度变化Fig.4 Graph of stick shadow length

图5 关系透视Fig.5 Relational perspective

5 结束语

本文研究将模拟退火算法应用于建筑优化设计问题，期望满足现有建筑日照约束要求条件下，自动计算在指定用地范围内拟建建筑最优高度.采用组合优化的思路及程序设计方法，应用于规划设计领域，实现合理的用地设计，与传统手工方式相比，软件分析快速，准确，高效，为节地设计提供了一种有效手段.

[1] 方勇.高层民用建筑设计在绿色建筑设计中的应用[J].土木建筑与环境工程,2016,38(7):72-74.DOI:10.11835/j.issn.1674-4764.2016.S1.015. FANG Y.The application of green building design in high rise building[J].Journal of Civil,Architectural & Environmental Engineering,2016,38(7):72-74.DOI:10.11835/j.issn.1674-4764.2016.S1.015.

[2] 王学宛,张时聪,徐伟,等.超低能耗建筑设计方法与典型案例研究[J].建筑科学,2016,32(4):44-53.DOI:10.13614 /j.cnki.11-1962 /tu.2016.04.10. WANG X W,ZHANG S C,XU W,et al.Research on design method of ultra-low-energy building and best practice[J].Building Science,2016,32(4):44-53.DOI:10.13614 /j.cnki.11-1962 /tu.2016.04.10.

[3] ECCIk L,LEPSIK P,PETRU M,et al.Modern methods of construction design[J].Lecture Notes in Mechanical Engineering,2014:209-233.DOI:10.1007/978-3-319-05203-8.

[4] ATTIA S,HAMDY M,O’BRIEN W,et al.Assessing gaps and needs for integrating building performance optimization tools in net zero energy buildings design[J].Energy & Buildings,2013,60(4):110-124.DOI:10.1016/j.enbuild.2013.01.016.

[5] MURRAY S N,WALSH B P,KELLIHER D,et al.Multi-variable optimization of thermal energy efficiency retrofitting of buildings using static modelling and genetic algorithms-A case study[J].Building & Environment,2014,75(3):98-107.DOI:/10.1016/j.buildenv.2014.01.011.

[6] FESANGHAR Y,ASADI M S,GEEM Z W.Design of low-emission and energy-efficient residential buildings using a multi-objective optimization algorithm[J].Buildings and Environment,2012,49245-49250.DOI:10.1016/j.buildenv.2011.09.030.

[7] 姜代红,刘一凡.基于分布估计算法的建筑结构设计优化[J].河北大学学报(自然科学版),2015,35(1):83-88.DOI:10.3969/j.issn.1000-1565.2015.01.015. JIANG D H,LIU Y F.Sructural design optimization based on estimation of distribution algorithms[J].Journal of Hebei University(Natural Science Edition),2015,35(1):83-88.DOI:10.3969/j.issn.1000-1565.2015.01.015

[8] FAGHIHI V,REINSHMID K F,KANG J H.Construction scheduling using genetic algorithm based on building information model[J].Expert Systems with Applications,2014,41(16):7565-7578.DOI:10.1016/j.eswa.2014.05.047.

[9] ASADI E,SILVA M G D,ANTUNES C H,et al.Multi-objective optimization for building retrofit:A model using genetic algorithm and artificial neural network and an application[J].Energy & Buildings,2014,81:444-456.DOI:/10.1016/j.enbuild.2014.06.009.

[10] TONG Z.A genetic algorithm approach to optimizing the distribution of buildings in urban green space[J].Automation in Construction,2016,72:46-51.DOI:/10.1016/j.autcon.2016.10.001.

[11] 成三彬.建筑日照分析及日照约束下最大容积率的计算[D].合肥：安徽理工大学,2011. CHANG S B.Architectural sunshine analysis and sunshine analysis and sunshine constraint under the maximum volume rate computation[D].Hefei:Anhui University of Science & Technology,2011.

[12] JUNGHANS L,DARDE N.Hybrid single objective genetic algorithm coupled with the simulated annealing optimization method for building optimization[J].Energy&Buildings,2015,86:651-662.DOI:10.1016/j.enbuild.2014.10.039.

[13] 康立山.非数值并行并法(第一册)：模拟退火并法[M].北京：科学出版社，1994.

(责任编辑：孟素兰)

High-rise buildings design optimization base on simulated annealing algorithm under the sunshine constraints

DANG Xiangying,JIANG Daihong， HUANG Xiaoling

(Jiangsu Key Laboratory of Smart Industrial Control Technology,Xuzhou Institute of Technology,Xuzhou 221000,China)

An optimization design approach to calculate building height based on simulated annealing method was proposed.Firstly,the building lands was divided evenly into several small grids，they were upwards stretched into small columns,and the total sunshine time was calculated according to the position relationship between the columns and window obscured.Then,the mathematical model of maximum building height based on minimum window sunshine time constraint was built.Finally,the building height was calculated based on the simulated annealing algorithm.Our experimental results demonstrate that the proposed method can accurately provide sunshine cumulative time under the constraints sunshine,and the maximum height was quickly obtained base on multiple disturbance of annealing mode.So the proposed method can provide an effective way for structure optimization design.

sunshine constraint;simulated annealing algorithm；volume rate；design optimization

10.3969/j.issn.1000-1565.2017.02.016

2016-04-01

江苏省建设系统科技计划项目(2014JH18);徐州市科技项目(KC15SH049);住房和城乡建设部科学技术项目(2014-K5-027)

党向盈(1978-),女,江苏徐州人，中国矿业大学在读博士，徐州工程学院副教授,主要从事建筑结构优化设计、进化算法研究.E-mail：dangpaper@163.com

TU972;TP

A

1000-1565(2017)02-0208-08