“变态”的压轴题

2017-04-26叶林

新教育时代·教师版 2017年9期

叶林

摘要：中考压轴题具有综合性强、信息点多、文字量大和逻辑性强等特点，使许多原本“实力”很强的学生望而却步！因此，此文精选了两道“压轴题”，通过抽丝剥茧般的分析，引导学生学会审题、运用数学的思维方法解题，感悟学习数学时夯实基础、总结提高的重要性；在提升学生分析问题、解决问题的能力的同时，帮助学生树立信心、消除对压轴题的畏惧之心。

关键词：心态数学思想以问题为中心悟和信心

一到初三下学期，每周进行一次模拟考，这不，小伍跑来：“叶老，这两道压轴题好变态”。

“别动不动说别人变态，也许是你见识不够广呢！”。

之前，我在班上跟学生讲过家庭教育方面的一个例子：当孩子摔倒，有些家长为安抚孩子，故作打将孩子拌倒的物体，可能是一块石头、也可能是一张凳子…..边打还边埋怨。看似有效，孩子不哭了嘛！可是，这样培养出来的孩子，今后只要出现失误或挫折时，他会习惯地从外部找原因，怨这怨那。看不到自己的问题，自然不会再有多少长进。

一次试卷讲评，很多孩子在一道最短距离问题上丢分，讲评时，小豪立马露出厌恶之情，见此情景，我问小豪：“轴对称、两点之间线段最短、含30°的直角三角形的三边关系，你熟悉吗？”

“熟悉啊！”

“你说说看”。

“……”。（此处省略60字）

接下来，我一步一步引导，用这几个小豪熟悉的知识点搞掂了这道题，小豪面露愧色，我又问：“这道题还变态吗？”

“不了，只怪我自己没想到”。

“学习中遇到难题，遇到挫折，其实很正常，关键是要摆正心态，强大自己。”

好了，下面，我们来看看这两道小伍口中“变态”压轴题所涉及的知识点和方法：

[题一]如图，在△ABC中，∠A=90°，AB=4，AC=3，M是AB上的动点（不与A，B重合），过点M作MN∥BC交AC于点N，以MN为直径作⊙O，并在⊙O内作内接矩形AMPN. 令AM=x.

（1）填空：当x=__________时，矩形AMPN的面积等于△ABC的面积？

（2）当x为何值时，⊙O与直线BC相切？

（3）在动点M的运动过程中，记△MNP与四边形BCNM重叠的面积为S，试求S关于x的函数表达式.

解：（1）易证：△ABC∽△AMN

∴

由

得

解得

（点评：此问是一基础题，涉及的知识是相似和图形的面积公式.）

（2）过点O作OH⊥BC，过点M作MH⊥BC

（点评：此处是个易错点，有同学误将点P当作切点。别怪出题人，好好看题，别人压根没说点P是切点.）

∵MN∥BC

∴OH=MH

易证：△BMH∽△BCA

可得MH=

由⊙O与直线BC相切，可得

OH=

∴

解得

（3）当时，

当时，

（点评：此题涉及分类讨论的数学思想，注意①把握x=2这个“界”，②体会图形从量变到质变的变化过程，也即重叠部分的图形从三角形变成梯形。在具体计算中，注意计算梯形MEFN的面积有多种方法。解完题之后，不妨小结一下，图中出现了哪些图形？如：矩形AMPN；□MBFN；□MECN；还有众多三边之比为3：4：5的相似三角形（包括全等三角形）…….）

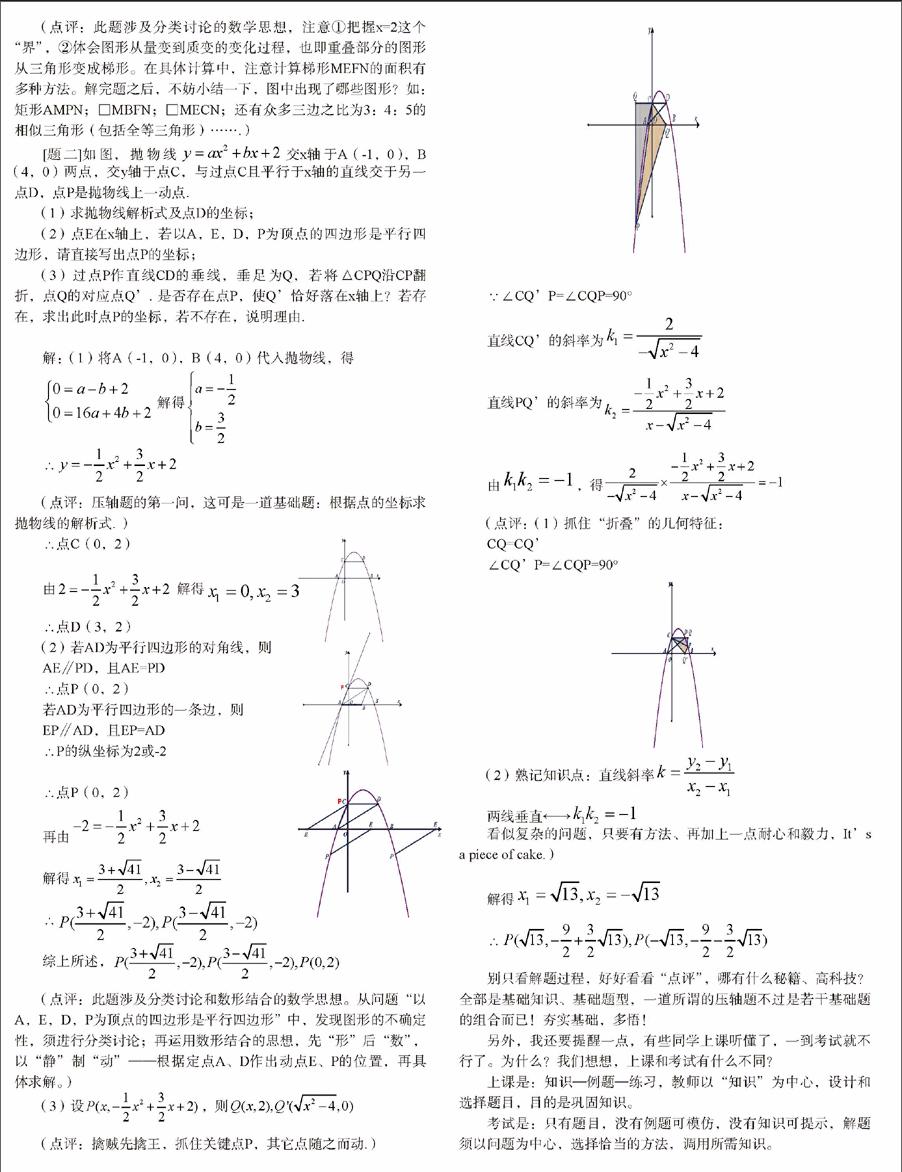
[题二]如图，抛物线交x轴于A（-1，0），B（4，0）兩点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点.

（1）求抛物线解析式及点D的坐标；

（2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，请直接写出点P的坐标；

（3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点Q. 是否存在点P，使Q恰好落在x轴上？若存在，求出此时点P的坐标，若不存在，说明理由.

解：（1）将A（-1，0），B（4，0）代入抛物线，得

解得

∴

（点评：压轴题的第一问，这可是一道基础题：根据点的坐标求抛物线的解析式. ）

∴点C（0，2）

由解得

∴点D（3，2）

（2）若AD为平行四边形的对角线，则