铯原子频标伺服优化技术的研究
2017-04-26王晓露高连山
王晓露,黄 凯,高连山
(北京无线电计量测试研究所,北京 100024)
铯原子频标伺服优化技术的研究
王晓露,黄 凯,高连山
(北京无线电计量测试研究所,北京 100024)
介绍了铯原子频标整机伺服优化的总体思路,详细分析了影响铯原子频标指标的各个参数,并提出了整机伺服优化的5个环路及其实现方案。通过试验验证所提出的伺服优化方案可行、有效。
铯原子频标;伺服环路优化;参数
0 引言
铯原子钟以其优良的长期稳定性和高可靠性的优势,成为世界一级频率标准和高精度基准钟,无论在地面守时系统还是在星载应用领域都发挥着巨大的作用。经过几十年的努力,我国铯原子钟的研制取得了一些成绩。目前国外商品化铯钟产品的一个共同特点是具备整钟伺服优化技术,通过对其内部状态的监测,由电路对影响其指标的各项参数进行实时监控,此功能决定了整机技术指标和使用寿命等关键因素。铯钟的整机伺服优化设计,减小了铯钟信号的漂移,延长了整机的寿命,提高了铯钟的频率稳定度和频率准确度指标,使其技术指标受温度、磁场和湿度的影响可以忽略不计。北京无线电计量测试研究所研制的铯原子钟具有整机伺服优化技术,其技术指标超越了5071A标准管的水平,接近5071A优选管的水平。本文将对铯原子钟的伺服优化技术的原理和实现加以介绍。
1 铯原子钟整机伺服优化的总体思路
当微波馈入信号以频率f扫描钟频时,铯束管输出的误差信号如图1所示。大共振信号(称为Rabi共振或Pedestal)的顶端为干涉条纹(Ramsey模式),条纹的中心线为馈入信号的参考频率,从而锁定晶振频率。此外,还有其他6条谐振线对称分布于中心谱线两侧(Zeeman线),间距均匀(其中的一条线如图1所示)。

图1 铯束管输出信号Fig.1 Output signal of cesium-beam tube
铯原子钟伺服优化的工作过程:
1)对铯原子钟输出的误差信号进行分析和判断,将埋于噪声中的有用信号提取出来,判断信号偏离方向;对晶体振荡器进行纠偏,当晶体振荡器处于正确的频率点时,停止控制直到发现新的偏离信号后再继续工作;
2)通过对多项铯束管参数进行测控,使处于跃迁环境中的铯原子保持稳定的状态。
2 铯束管参数及环境变化对铯原子钟的影响
(1)C场电流变化对频率准确度的影响
设置C场电流为12.0000mA、12.50000mA和13.0000mA,测量在每一个C场电流下铯原子钟的频率准确度,数据如表1所示。

表1 C场电流与频率准确度关系
从表1可以看出,不同的C场电流,铯原子钟的频率准确度不同。
(2)微波功率变化对频率准确度的影响
我们设置微波功率为-6.5dBm、-7.0dBm(最佳微波功率)和-7.5dBm,测量在每一个微波功率下铯原子钟的频率准确度,数据如表2所示。

表2 微波功率与频率准确度关系
从表2可以看出,不同的微波功率,铯原子钟的频率准确度不同。
(3)外界环境温度对频率准确度的影响
改变外界环境温度,测量频率准确度的改变(对铯钟不进行伺服优化),数据如表3所示。
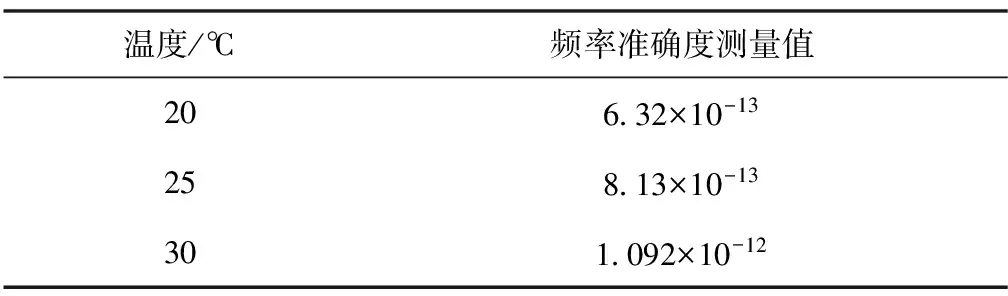
表3 外界环境温度对频率准确度的影响
从表3可以看出,随着外界环境温度变化,铯原子钟的频率准确度也发生了变化。
C场电流和微波功率都是由电路产生的,电路本身存在小范围的漂移现象。因此,不可避免地造成C场电流和微波功率的变化,而且外界环境也会发生改变。因此,要保证铯原子钟的长期稳定特性,铯原子钟的伺服优化是很有必要的。
3 铯原子钟伺服优化的实现
铯原子钟的整机伺服优化需要5个独立的稳定调节环路,分别是主控制环路、铯炉稳定环路、C场自动调节环路、微波功率自动调节环路和电子倍增器自动调节环路。
(1)主控制环路
10MHz晶体振荡器的锁定是铯原子钟的主控制环路,也是最基本的自动控制环。锁定的基本原理如图2所示。

图2 10MHz晶体振荡器伺服原理示意图Fig.2 Principle of 10MHz crystal oscillator servo loop
铯原子钟在进行频率锁定时,需要在微波频率上加一个调制信号。在这里使用方波调制,可以改善互调效应给被动式频标引入噪声,从而提高了频标的稳定度,如图2所示。
在中心频率9192631770Hz上下等距离的位置(中心峰的3dB带宽)分别将产生的方波调制微波信号馈入到铯束管中,当不同的激励信号进入微波腔与铯原子作用后,将产生不同幅度的强度信号,通过对误差信号的采集可以获取中心频率与跃迁频率偏差,这一信息可以指导主控制环路对10MHz晶振进行纠偏,当达到锁定状态时,误差信号将为0。伺服系统还具有判断误差信号是否为频率偏差的判断能力,当受外界干扰时,伺服系统能够对干扰进行排除,同时,当达到锁定状态时,停止对10MHz纠偏,消除伺服系统的固有误差。
(2)铯炉稳定环路
根据铯束管研制方提供的热敏电阻值与铯炉温度的关系,将炉温控制在合适的工作温度上,并保证炉温的变化不会影响铯原子钟性能。
铯炉温度的精确控制采用电桥平衡方法。调整炉温控制放大器的输入电压,控制加热元件,通过反馈电压实现铯炉的自动控制。试验表明,在达到设定的炉温后,热敏电阻值变化<1Ω,对应的温度与电阻值对应曲线为1℃/80Ω,因此控温精度为<0.0125℃。图3所示为铯炉的炉温控制过程,可以看出,在控制的初始阶段会产生一些震荡,之后逐渐平稳,铯炉温度可以稳定在<0.0125℃。

图3 铯炉电阻控制过程Fig.3 Control process of cesium stove resistance
(3)C场自动调节环路
C场的作用是:
1)使mF=0的态从其他超精细磁能态中分离出来;
2)使A磁铁中建立的原子磁能态不致因通过零磁场而混杂;
3)提供空间取向以选出σ跃迁。
C场值的变化将直接导致铯原子钟频率准确度的变化。因此,必须对C场电流,也就是对铯束管中的辐射场相互作用区和漂移区的恒定磁场,进行稳定控制。根据原子跃迁频率与磁场强度的关系

(1)来确定C场电流值。式中,ν0为9192631770Hz,ν(0-0)为使原子发生跃迁的微波激励信号频率,H0是磁场强度,单位为高斯。同时对C场进行稳定控制,控制精度为波动<0.01%。
但是,实际情况是即便达到了上述的C场电流稳定度要求,由于环境温度等外界因素发生变化,C场结构也会发生变化;C场结构材料剩余磁场随环境变化而变化;外界磁场的变化等因素都能够引起场强发生变化。要解决由于C场场强变化带来的问题,必须对C场实现闭环控制,随外界变化而改变C场电流,保证C场场强强度一致,从而获得较高指标的长期频率稳定度。
对于ΔF=±1,ΔmF=0的跃迁,跃迁频率为
ν(4,mF↔3,mF)=ν0+7.0083×105mFH0+
(2)
对于mF=±1的2个跃迁频率差为
Δν=ν(4,+1↔3,+1)-ν(4,-1↔3,-1)=2×7.0083×105H0
(3)
从式(2)和式(3)可知,C场场强与mF=±1的2个跃迁频率差呈正比,可以通过调整C场电流值来保证mF=±1的2个跃迁频率差不变,从而保证C场场强的一致性。因此,C场伺服优化的重点在于如何准确地测量mF=±1的2个跃迁频率。
图4所示为扫描铯束管mF=+1峰的曲线图。从图4中可以看出,mF=+1峰是不对称的,这一点与中央峰不同,这个不对称性是由铯束管的工艺决定的。
C场电流闭环控制的方法有两种。
方法1:根据式(1),设定中心频率后,C场电流随之确定。在mF=+1或者mF=-1峰的微波频率附近,施加调变频率将检测到误差信号,这个误差信号在实际磁场强度与设定值一致时,将达到最小值,以此来判断C场电流是否为最佳C场电流。这个方法与主控制环路的方法相似,但是由于铯束管的制作工艺问题,mF=±1峰很难做到像中央峰一样的对称,如图4所示。因此,采用方法1进行C场伺服优化时会存在一个固定偏差。

图4 铯束管mF=+1峰曲线图Fig.4 The curve of cesium-beam tube mF=+1 apices
方法2:当整钟锁定后,微波馈入信号扫描9192666770~9192681770Hz频率确定mF=+1峰的频率值,扫描9192581770~9192596770Hz频率确定mF=-1峰的频率值。采用曲线拟合的方法来确定mF=±1峰的频率值。经过分析采用256个点的曲线拟合,最小值即为mF=±1峰的频率值,如图5所示。

图5 256个点曲线拟合Fig.5 Curve fitting of 256 dots
(4)微波功率自动调节环路
微波激励信号功率的漂移是影响铯束频标长期稳定工作的主要因素之一。微波功率的变化是通过Rabi牵引影响频标准确度的,Ramsey腔的微波泄漏不仅会给铯束频标引入频移,也能够增大频标对微波功率变化的敏感度。多份资料指出,微波功率频移对铯束频标性能影响显著,需要控制微波功率,应使微波功率变化小于0.05dB。与C场电流一样,多种外界因素譬如环境温度的变化等将使微波腔产生一定的形变,使铯原子感受到微波功率发生了变化。也就是说,即使微波功率保持不变,但外界因素仍能使实际发生作用的微波功率发生变化。我们通过对微波功率的伺服控制,达到使原子感受到稳定的微波功率,最终提高了频率长期稳定度。
微波功率的伺服优化分为两部分:开机最佳微波功率的自动调整和伺服过程中微波功率的自动调整。
在铯原子钟开机,铯束管、晶体振荡器达到工作温度后,电路系统启动最佳微波功率调整,自动搜索得到最佳微波功率,并以此功率进行闭环锁定。在主环路闭环锁定过程中,实时监测微波功率与输出误差信号的变化关系趋势,进而来调整微波功率,使微波功率始终保持稳定。
通过在不同微波功率下,对铯束管进行Ramsey扫描可以发现,相同的微波激励频率信号在携带不同的能量进入微波腔内与铯原子作用时,引起的铯原子跃迁数量不同,也就是说同样微波频率不同微波功率的激励信号,将导致铯束管输出的荧光信号大小不同。
在不同微波功率条件下,对铯束管Ramsey线形进行测量,测量结果如表4所示。

表4 微波功率与峰值关系
从表4可以看出,存在一个最佳的微波功率值,在这个微波功率作用下,Ramsey线形的峰值和峰峰值均最大,对微波功率的伺服就是利用这样一个特点进行的。在最佳微波功率时,荧光信号最强,比最佳微波功率大一点或者小一点所获得的荧光信号都较小。图6所示为中心频率峰值随微波功率的变化趋势图。其中中心频率峰值最大处对应的微波功率就是铯钟的最佳微波功率。

图6 中央峰值随微波功率变化曲线图Fig.6 The curve of peak value changed with microwave power
从图6可以看出,中心频率峰值随微波功率的变化具有明显的不对称性。这里我们采用256个点曲线拟合的方法来确定最佳微波功率。
(5)电子倍增器自动调节环路
从我们所掌握的针对国外和国内铯束管试验结果和理论分析得到:电子倍增器放大量将随着工作时间的增长而变小。当中央峰的峰峰值达到一定门限后,铯原子钟就能够稳定工作,小于这个门限就无法正常工作,因此,必须也只能通过增大电子倍增器的供电电压,也就是增大电子倍增器的级间电压来弥补放大量的变小趋势。电子倍增器还具有这样的一个特性:工作电压越高,性能下降越快。因此,在满足门限的前提下,电子倍增器电压有一个从小到大逐渐变化的控制过程。
电子倍增器的自动调整的关键是判断是否达到铯原子钟稳定可靠工作的门限。通过测量判断合理地选择电子倍增器电压能够保证频标高指标输出。
4 铯原子钟测试
(1)伺服优化系统配合5071A铯束管测试结果,如图7所示。

图7 伺服优化系统配合5071A铯束管测试结果Fig.7 The results of 5071A cesium-beam tube with servo loop system
(2)伺服优化系统配合国产磁选态铯束管测试结果,如图8所示。

图8 伺服优化系统配合国产磁选态铯束管测试结果Fig.8 The results of domestic magnetic state-selecting cesium-beam tube test with servo loop system
(3)伺服优化系统配合国产光抽运铯束管测试结果,如图9所示。

图9 伺服优化系统配合国产光抽运铯束管测试结果Fig.9 The results of domestic optical pumping cesium-beam tube test with servo loop system
5 结束语
铯原子钟伺服优化在整钟的工作过程中起到了重要作用,它是整钟得以稳定、可靠工作的核心。伺服优化通过5个环路使处于跃迁环境中的铯原子保持稳定的状态,保证了铯原子钟的频率准确特性和长期稳定特性。
[1] 王义遒,王庆吉,傅济时,等. 量子频标原理[M]. 北京:科学出版社,1986.
[2] Percival R,Green C.On an improved method of resolving the frequency difference between two very accurate and stable frequency signals[C]//31stAnnual Precise Time and Time Interval(PTTI)Meeting, 1999: 637-648.
[3] Audoin C, Hamouda F, Chassagne L, et al. Controlling the microwave amplitude in optically pumped cesium beam frequency standards[J]. IEEE Transactions on Ultrasonics,Ferroelectrics, and Frequency Control, 1999, 46(2): 407-413.
[4] Kang H S. Comparison of the Rabi and Ramsey pulling in an optically pumped cesium-beam standard[J]. Metrologia,2003,40(5):224.
[5] 刘春侠,王改霞,漆溢. HP5071A铯原子钟内部工作参数的监视与分析[J]. 时间频率学报,2004,27(1):54-63.
[6] Lacey R F. Phase Shift in Microwave Ramsey Structure[C]//Proceedings of the 22thAnnual Symposium Frequency Control,1968: 545-558.
[7] Audoin C, Lesahe P, Mungall A G. Second-order doppler and cavity phase dependent frequency shifts in atomic beam frequency standard[J]. IEEE Transactions on Instrumentation Measurement, 1974,23(4): 501-508.
[8] Hellwig H,Jarris S,Glaze D J,et al. Time domain velocity selection modulation as a tool to evaluate cesium beam tubes[C]//Proceedings of the 27thAnnual Symposium Frequency Control,1973:357-366.
[9] 肖顺禄,陈海军,梁友焕. 磁选态铯束管铯原子速度分布计算[C]//全国时间频率标准学术会议,2007: 123-125.
[10] 郭媛,黄秉英. 用于铯原子钟性能研究的单片机数字伺服[J]. 宇航计测技术,1998,18(1):56-61.
Research on the Servo Loop Optimization of Cesium Frequency Standard
WANG Xiao-lu, HUANG Kai, GAO Lian-shan
(Beijing Institute of Radio Metrology & Measurements, Beijing 100024, China)
The general idea of Servo Loop in Cesium Frequency Standard is introduced. The parameters of affecting Cesium Frequency Standard performance are analysed. And the five optimized loops and their solutions of Cesium Frequency Standard Servo Loop are proposed. Experiment result shows the method discussed here is useful.
Cesium frequency standard; Servo loop optimization; Parameters
2016-11-15;
2016-12-07
王晓露(1980-),女,硕士,高级工程师,主要从事原子钟电路设计方面的研究。E-mail:xiaoluws@163.com
10.19306/j.cnki.2095-8110.2017.02.011
U666.12
A
2095-8110(2017)02-0058-06
