输电线路电场计算的非连续网格有限元法

林育艺　林燕鸿



输电线路电场计算的非连续网格有限元法

林育艺1林燕鸿2

（1. 深圳供电局有限公司，广东深圳 518010；2. 国网龙岩供电公司，福建龙岩 364000）

本文利用有限元方法计算了输电线路沿线的电场，同时利用分界面自由度耦合的非连续网格法进行网格剖分，提高了计算效率。经500kV交流输电线路模型计算分析得出，在距离地面1.5m处电场强度未超过国家标准限值。论证了分界面自由度耦合的非连续网格有限元法适用于“大尺寸区域小尺寸元件”模型的网格剖分，适用于输电线路电场的计算。

输电线路；电场；有限元法；非连续网格

随着我国特高压技术的迅速发展，输电线路所产生的电场问题越来越受到人们的关注。准确地计算输电线路的电场，将有助于对输电线路沿线居民受其影响状况进行初步评估，并且在线路设计中起着非常关键的作用。

目前，输电线路周围电场数值计算方法主要有两种：①模拟电荷法[1-2]；②有限元法[3-5]。采用模拟电荷法时应先确定模拟电荷的大小和位置，其计算精度由模拟电荷的精确程度确定，同时匹配点的选取对计算精度也有一定的影响。此外，当考虑杆塔、房屋、地面不平等复杂边界条件和求解区域中存在介质块等问题时，采用模拟电荷法将会出现模拟电荷个数和位置较难确定的问题。而有限元方法在不规则场域的计算上相比于模拟电荷法具有优越性，并且有通用的计算程序，使用方便。但是，为了得到较为精确的计算结果，需要对导线的周围细分，由于导线的尺寸是mm数量级的，而空间求解区域是m数量级的，两者的尺寸相差较大，这使得剖分单元数大增，计算效率低，因此，网格的剖分方式是模型计算精度和效率的关键。

针对有限元网格剖分的优化已有一定的研究成果。文献[3]推导了两种无限长直导线三维空间电场强度计算公式，在确定求解区域和求解边界后，先利用公式计算三维截面上各点的场强值，然后将计算结果作为边界条件代入软件仿真。这种方法减小了求解区域，提高了计算效率。但是，边界条件的计算是用了近似计算，可能会降低计算精度。文献[4]利用分域思想将结构复杂的绝缘子及其表面空间作为细剖分区域，杆塔、导线及外部空间部分作为辅助计算区域，对细剖分区域和辅助计算区域进行迭代计算得到最终的电场分布。这种方法克服了大型有限元模型剖分难度大以及计算时间长的缺点，但是引入了迭代算法，使问题变得更加复杂。因此，本文提出了分界面自由度耦合的非连续网格有限元法，不仅不必缩小求解区域，也不必迭代计算，还能有较高的计算精度和计算效率。

1 非连续网格有限元法有效性验证

1.1 分界面自由度耦合法

传统的有限元方法要求在求解区域的分界面两侧网格的数量必需一致，分界面上的节点必须被两侧网格共用（如图1（a）所示）。由于输电线的尺寸很小，而求解区域尺寸相对较大，因此，在导线附近的网格单元尺寸必须很小，这将导致由小尺寸网格到匹配大的求解区域的大尺寸网格过渡过程中的过渡网格数量相对庞大，进而降低计算效率。

分界面自由度耦合法能够较好地解决这一问题。此方法不必要求分界面两侧的网格的连续性（如图1（b）所示）。这样就能够有效地减少网格数量，提高计算效率。并且，ANSYS软件提供了分界面自由度耦合法，利用此方法可以较好地解决本类模型的网格剖分问题。

（a）传统有限元法

（b）分界面自由度耦合法

图1 传统有限元法与分界面自由度耦合法的网格剖分对比图

该方法使用的基本思路如下：首先，在建立几何模型时，两个求解区域不进行布尔运算，具有独立的分界面；然后，独立对两个求解区域进行网格剖分；网格剖分完成后，选取利用小网格剖分的区域分界面上的所有节点，定义为节点组件，再选取大网格剖分的区域中包含分界面上节点的所有单元，定义为单元组件；最后，将节点和单元进行自由度耦合。

1.2 方法正确性验证

图2为文献[5]给出了直流模拟试验线路的空间结构图。空间尺寸和施加的电压如图2所示，两条正、负极导线型号均为LGJ-95，导线半径为6.935mm。

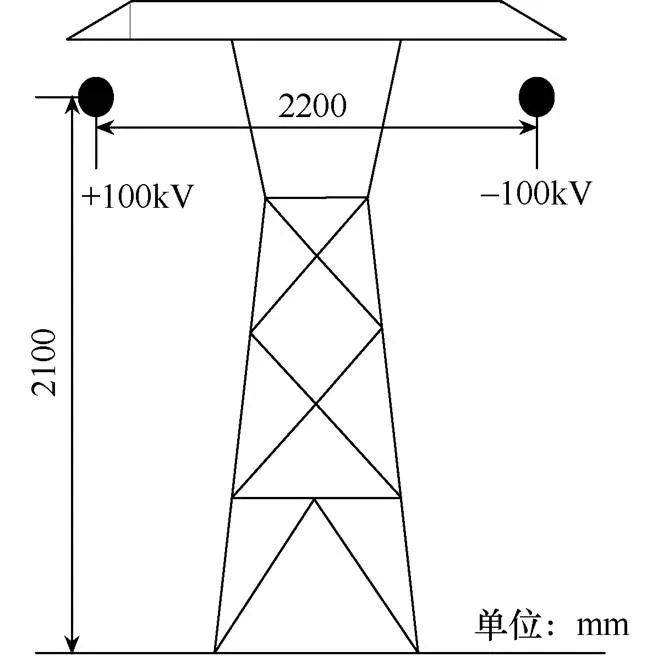
图2 直流模拟试验线路的空间结构图

当不考虑线路弧垂、忽略杆塔等对电场的影响、假设线路足够长时，可用二维平面模型来近似计算直流线路的标称电场。模型建立时，导线外先建立一层求解区域，其半径为0.3m。整体求解区域外建立远场区域，用远场单元来模拟无穷远电位为零。

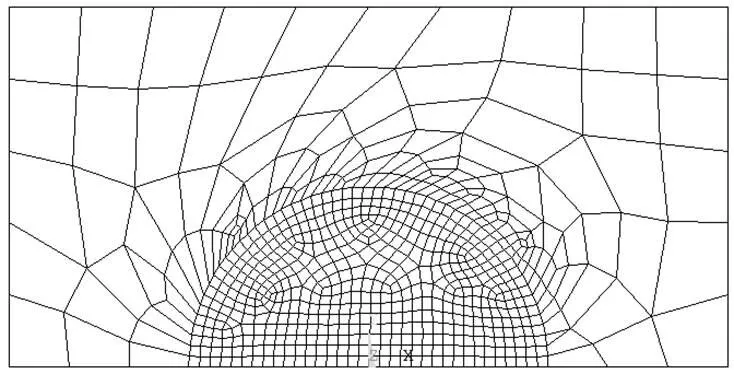
网格剖分时，导线外的小求解区域和整体的求解区域是独立剖分网格，然后再将自由度耦合。图3为导线部分网格剖分示意图，由图中可以看出分界面两侧的网格尺寸相差较大。经计算发现，在同等剖分精度下，采用自由度耦合法所需的单元个数为9217个，而采用传统的有限元剖分方法所需的单元个数为23043个，并且计算的电位相对误差不超过1.5%。由此可见，在自由度耦合法在误差允许范围内，节省了大量的单元，在计算效率上相比于传统有限元剖分法具有明显的优越性。

图3 导线部分网格剖分示意图

通过模型计算直流线路的标称电场，得到整个求解区域的电位等位线分布，如图4所示。图5为模型计算得到的近地面（距离地面0.1m处）的标称电场场强沿水平方向的分布图，其与文献[5]给出的标称电场的计算结果完全吻合。

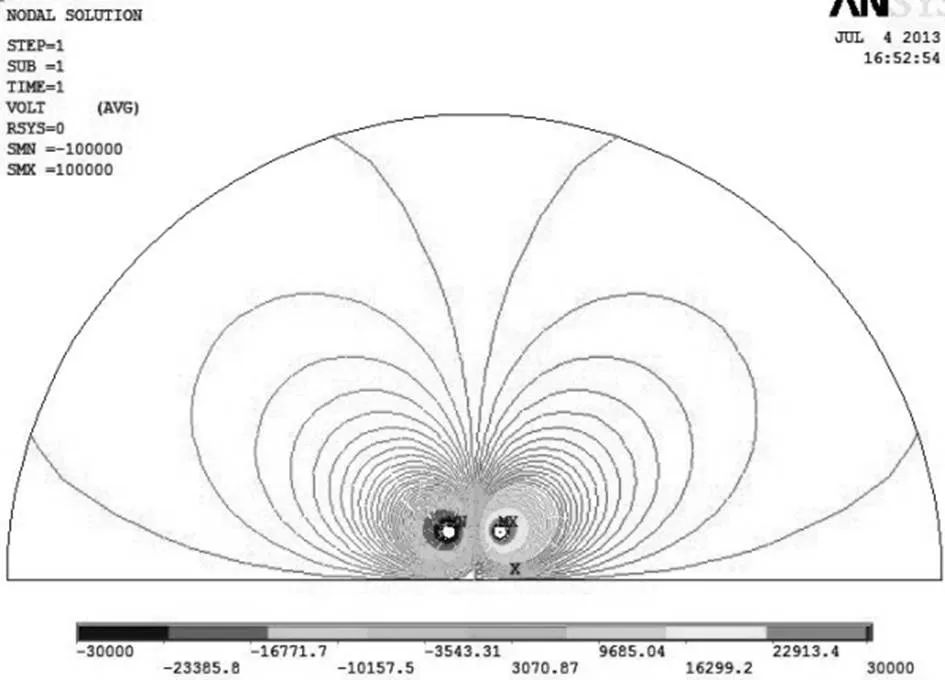
图4 求解区域电位等位线分布图

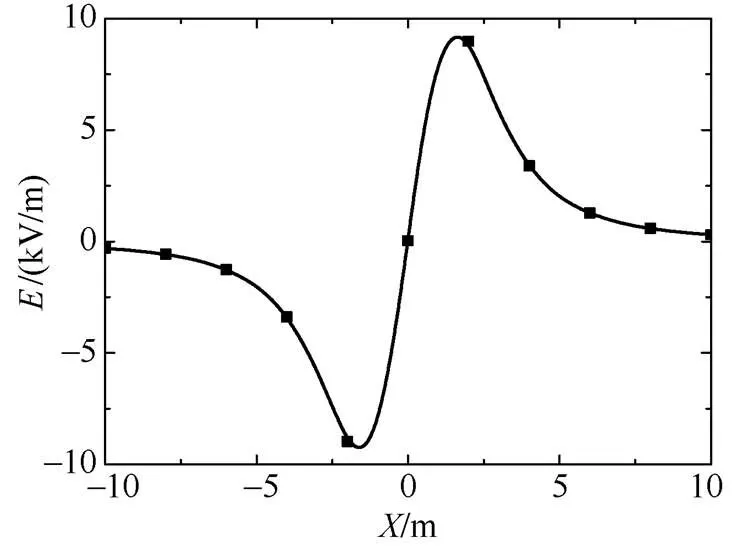
图5 求解区域电场强度分布图

针对此问题，假设导线无限长，导线足够细，则可以利用镜像法进行求解。为了比较镜像法和非连续网格有限元法的计算结果，选取距离地面高度分别为2m、1.5m、1m、0.5m的水平参考线的电位值进行比较，得到如表1所示的参考线上相对误差最大值。由表1可以看出，相对误差不超过1%，计算精度符合工程要求。虽然在此问题中，镜像法算法简单且精确，但是，当考虑杆塔、房屋、地面不平等复杂边界条件和求解区域中存在介质块等问题时，采用镜像法将会出现模拟电荷个数和位置很难确定的问题。而有限元方法在不规则场域的计算上具有优越性，并且有通用的计算程序，使用方便。综上，分界面自由度耦合的非连续网格的有限元法在计算电场问题中，不仅单元数目大大减少，而且提高了计算效率和很高的计算精度，是计算电场问题的有效方法。

表1 离地不同高度与镜像法相比最大相对误差

2 500kV交流输电线路的工频电场计算

本文将以500kV交流输电线路建立计算模型，通过算例分析，分析输电线路的工频电场情况，以期说明仿真计算对工程设计具有参考意义。

2.1 模型设置

图6为500kV交流输电线路的整体模型示意图，参数设置如图所示。输电线路导线型号为4×LGJ-400/35，子导线半径为13.41mm，导线分裂间距为450mm，四根子导线呈正方形布置[6]。由于导线尺寸较小，因此，先在每一子导线外建立半径为150mm的求解区域，再在每一相导线外建立半径为2m的求解区域。图7为导线附件网格剖分示意图，由图中可以看出，不连续网格剖分使得在各分界面两侧的网格尺寸相差很大，减少了大量的过渡网格，因此，有限元计算效率将大大提高。

图6 500kV交流线路整体模型示意图

图7 导线附近网格剖分示意图

2.2 计算结果分析

经模型计算得到A相相位分别为0°和90°的空间电位分布图如图8所示。

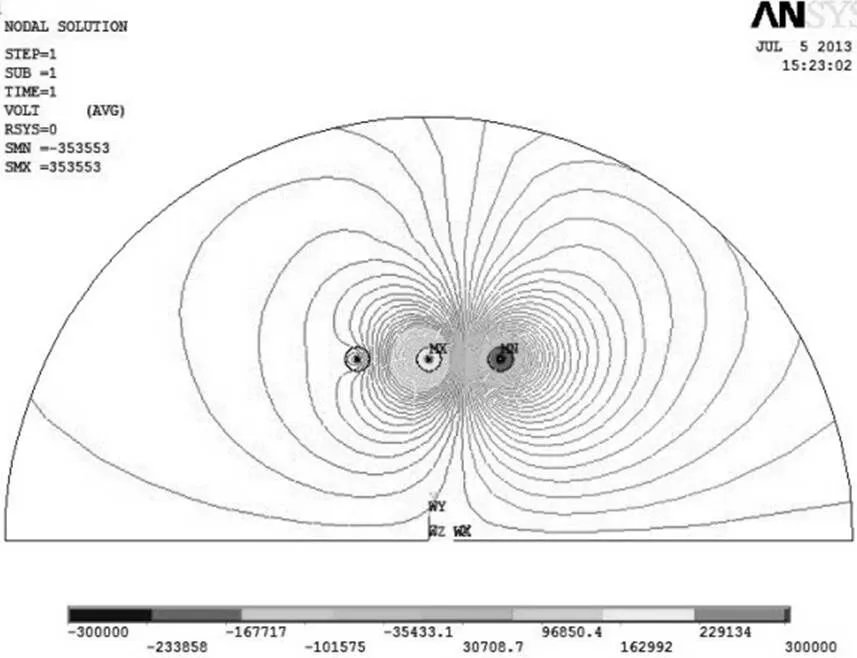
（a）A相相位为0°

（b）A相相位为90°

图8 求解区域电位等位线分布图

我国环境指标规定，推荐暂以离地1.5m处，4kV/m作为居民区工频电场评价标准[7]。因此，利用模型计算得到A相相位分别为0°，45°，90°，135°情况下距离地面1.5m处的不同水平距离下的电场强度如图9所示。由图中可以看出，不同相位下，电场强度最大值的幅值和产生的位置都发生了变化。将不同相位下，距离地面1.5m处的电场强度最大值整理得到如图10所示的分布图。由图10可得，在距离地面1.5m处的电场强度不超过2.5kV/m，未超过国家标准限值。

图9 A相不同相位情况下距离地面1.5m处的空间电场强度分布图

3 结论

本文研究了输电线路沿线电场的有限元计算方法，提出了一种计算效率高的网格剖分方法。

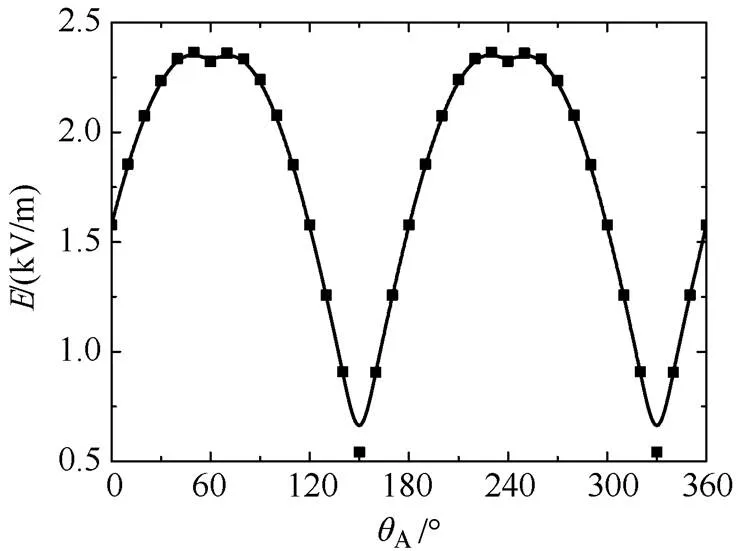
图10 A相不同相位情况下距离地面1.5m处的电场强度最大值分布图

1）分界面自由度耦合的非连续网格有限元法计算效率和精度都比较高，适用于“大尺寸区域小尺寸元件”模型的网格剖分，是计算输电线路电场问题的有效方法。

2）本文所计算的500kV交流输电线路，在距离地面1.5m处的电场强度未超过国家标准限值。

3）本文仅以二维平面模型为例，论证了非连续网格有限元法的适用性和高效性，针对三维模型，此方法也是适用的，而且相比于二维模型，三维模型的计算效率提高得更加明显。

[1] 俞集辉, 周超. 复杂地势上超高压输电线路的工频电场[J]. 高电压技术, 2006, 32(1): 18-20.

[2] 邹澎. 高压输电线下有建筑物时工频电场的数学模型[J]. 中国电力, 1997, 30(3): 13-15.

[3] 王晓燕, 赵建国, 邬雄, 等. 交流输电线路交叉跨越区域空间电场计算方法[J]. 高电压技术, 2011, 37(2): 411-416.

[4] 武坤, 司马文霞, 杨庆, 等. 分域迭代法计算特高压线路绝缘子电场分布[J]. 高电压技术, 2009, 35(6): 1279-1283.

[5] 甄永赞, 崔翔, 罗兆楠, 等. 直流输电线路三维合成电场计算的有限元方法[J]. 电工技术学报, 2011, 26(4): 153-160.

[6] 李永明, 范与舟, 徐禄文. 超高压输电线路铁塔附近地面工频电场仿真分析[J]. 电网技术, 2013, 37(3): 782-787.

[7] 1998 H J T. 500kV超高压送变电工程电磁辐射环境影响评价技术规范[S].

Calculation of Electric Field of Transmission Lines by the Finite Element Method with Discontinuous Mesh

Lin Yuyi1Lin Yanhong2

(1. Shenzhen Power Supply Bureau Co., Ltd, Shenzhen, Guangdong518010;2. State Grid Longyan Power Supply Company, Longyan, Fujian364000)

In this paper, the electric field is calculated by the finite element method. By calculation and analysis of the 500kV AC transmission lines model, this paper draws a conclusion that the electric field intensity is less than the national standard limit at 1.5m above the ground. In the calculation, the mesh generation with the freedom coupling method on interfaces is adopted to model the thin transmission lines and the large surrounding air region, and is appropriate for calculating electric field of transmission lines. This method is able to reduce the demand of element numbers and increase the calculation accuracy heavily.

transmission lines; electric field; finite element method; discontinuous mesh

林育艺（1990-），男，广东省深圳市人，硕士，主要从事电网规划相关工作。