基于EEMD的HHT在电能质量多扰动分类识别中的应用
2017-04-25曹玲芝刘俊飞郑晓婉
曹玲芝 刘俊飞 郑晓婉
基于EEMD的HHT在电能质量多扰动分类识别中的应用
曹玲芝 刘俊飞 郑晓婉
(郑州轻工业学院,郑州 450002)
现有的电能质量扰动分类识别方法对电能质量多扰动的分类准确性和识别能力较低,本文提出了将基于聚类经验模态分解(EEMD)的希尔伯特—黄变换(HHT)应用于电能质量多扰动的分类识别方法。它依据电能质量多扰动信号就是在电能基波上叠加不同频率和不同幅值波形的特性,首先利用EEMD对含扰动信号分解得到信号的固有模态函数(IMF),滤除残余噪声后,将得到的IMF分量作为特征值对扰动进行分类,再对IMF进行Hilbert变换得到其瞬时频率和瞬时幅值,瞬时频率的突变点反映电能质量扰动的起止时刻,瞬时幅值反映电能质量扰动的幅度,根据对突变点的观测实现对各个扰动的准确识别。Matlab仿真分析结果表明,该方法能够准确的对电能质量多扰动的扰动类型进行分类,并确定电能质量各个扰动信号的时间、幅值和频率。
电能质量多扰动;希尔伯特-黄变换;聚类经验模态分解
电能质量扰动的分类识别一直是电能质量问题研究的核心课题,近年来研究电能质量扰动识别的方法越来越多,大部分学者主要使用小波变换法[1-4]、短时傅里叶变换[5-6]、S变换[7-9]、数学形态学等数学理论及其他方法[10-15]对扰动信号进行分析,取得了大量的研究成果,能够对电能质量的单一扰动进行准确的分类识别,只有少部分学者针对两种同类扰动进行叠加研究[16],研究对象与实际电能质量扰动信号差距太大,研究成果实用性不强。因此,研究一种能够同时对电能质量中叠加的多种扰动进行分类识别的方法,对电能质量问题的研究具有重要的意义。
针对此问题,本文利用HHT的自适能力和精确识别能力,同时为了解决HHT过程中经验模态分解(EMD)造成的模态混叠和过零点失效现象,提出了用基于EEMD的HHT方法对电能质量多扰动进行分类识别的方法。由于EEMD方法是按照频率由高到底的顺序将信号分解成不同的IMF,所以对IMF去噪后,每一个IMF就是一种频率的扰动特征成分(由于频率相同,电压中断、暂降、暂升仍存在与基波中),根据IMF的波形以及对IMF进行Hilbert变换后得到的瞬时频率和瞬时幅值波形,可以对扰动信号进行准确分类识别。仿真结果表明,该方法可以对复合扰动进行准确识别分类,并根据对IMF分量的Hilbert变换,在时间和幅值上准确地对各种扰动进行定位定量的描述。
1 电能质量扰动的分类和特征
目前电能质量扰动分类识别研究中主要的研究对象为谐波、电压中断、暂态脉冲、暂态震荡、电压暂升和电压暂降。本文按照扰动时参数突变的不同性质对这些扰动进行了划分,确定了两种扰动类型,分别为加性扰动和幅值扰动,见表1。其中加性扰动由于其频率与基波频率不同,按照EEMD按频率由高到低分解原则,可以将加性扰动的特征分量分解到不同的IMF中;而幅值扰动由于其频率与基波频率相同,在进行EEMD分解时,不能将其分解为单独的IMF分量,其扰动特征仍包含于基波IMF分量中,通过Hilbert变换得到基波IMF分量的瞬时频率和瞬时幅值进行分类识别。

表1 电能质量扰动类型的分类
2 基于EEMD的HHT方法原理
HHT方法的关键是EMD,它能使复杂信号分解为有限个IMF,所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征信号。但是EMD在分解的过程中存在严重的模态混叠问题,在同一个IMF中包含有不同时间特征尺度的特征分量,无法对扰动进行有效地分类识别。
针对EMD的模态混叠问题,Zhaohua Wu和N. E. Huang等人提出了EEMD方法。EEMD的分解过程如下[17]:
1)添加高斯白噪声到目标信号。
2)用EMD法将添加后的信号分解为IMF。
3)重复步骤1和2,但每次添加的白噪声是随机的。
4)将每次分解的IMF做均值后,作为最后的分解结果。
为了更好的提取信号的扰动特征,引入瞬时频率和瞬时幅值对扰动进行分析。首先对得到的IMF分量进行Hilbert变换:

对变换后的信号进行反变换,即
(2)

(4)
瞬时频率为
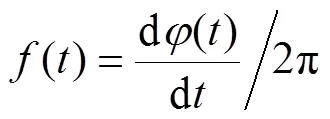
本文将基于EEMD的HHT方法应用于多扰动信号的识别问题,首先对待检测信号做EEMD分解处理,对得到的若干个IMF分量给出适当的阈值进行筛选并进行信号的重构,即得到单一成分的信号,此时对该单一信号进行希尔伯特变换,再根据变换后得到的信号的瞬时幅值、瞬时频率描绘的图谱对其扰动类型进行分析。
3 电能质量多扰动分类识别仿真分析
利用Matlab软件对表1中的几种电能质量扰动进行叠加,并通过本文提出的方法进行分类识别的仿真。为了验证本文方法对多扰动的有效性和准确性,分别对2个、3个和5个扰动信号进行仿真。
3.1 暂态震荡和暂态脉冲复合扰动
Matlab编程产生暂态脉冲和暂态震荡信号,设置基波信号频率为=50Hz,暂态震荡发生的时间区间为0.16~0.17s,震荡频率z=500Hz,震荡幅度为0.8V;暂态脉冲发生的区间为0.19~0.191s,脉冲幅度为1.5V,采样频率为s=8kHz。仿真波形如图1所示。
由图1(a)可以看出,IMF1为原始信号中含有暂态震荡和暂态脉冲扰动部分,图1(b)中暂态震荡和暂态脉冲的检测参数见表2。

(a)原始信号和EEMD分解图
(b)IMF1信号的Hilbert变换
图1 震荡和脉冲信号HHT仿真分析
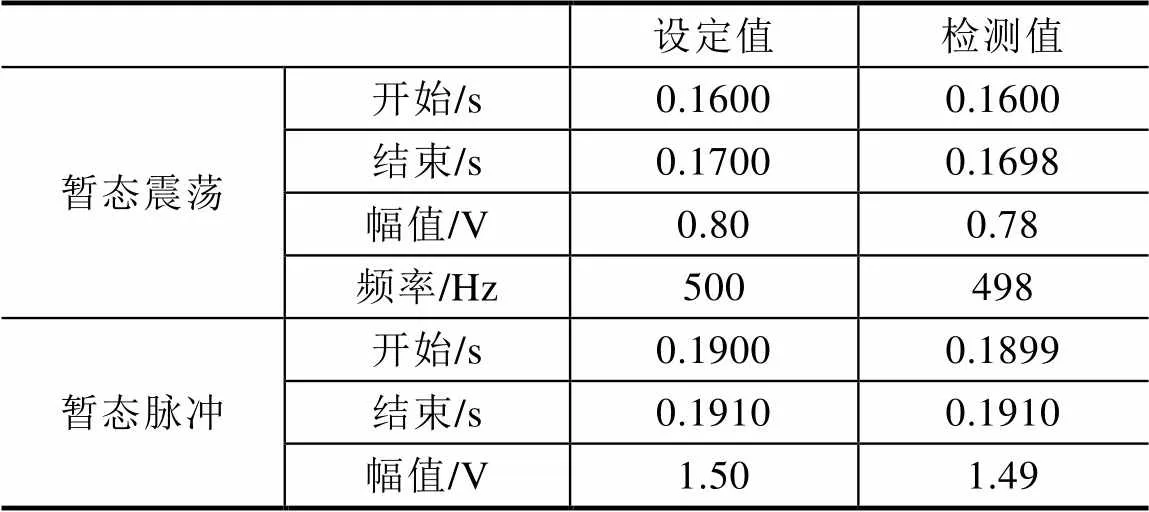
表2 暂态振荡和脉冲信号参数检测结果
3.2 电压暂降、电压中断、暂态震荡复合扰动
设定基波信号频率=50Hz,电压中断时间为0.08~0.12s,暂降时间为0.16~0.24s,暂降幅度为0.5p.u.,暂态震荡时间为0.16~0.17s,震荡频率z=500Hz,震荡幅值为0.8V,采样频率为8kHz。仿真波形如图2所示。

(a)原始信号和EEMD分解图
(b)IMF信号的Hilbert变换
图2 暂降、中断和震荡信号HHT仿真分析
在图2(a)中,IMF1为原始信号中的高频震荡信号,IMF2为原始信号中的低频部分。对IMF1 和IMF2进行Hilbert变化,由图2(b)的瞬时频率和瞬时幅值确定各扰动的参数见表3。

表3 电压暂降、暂态振荡和脉冲信号参数检测结果
3.3 谐波、电压暂降、暂态震荡和暂态脉冲复合扰动
仿真参数设置如下:在信号中加入3次和5次谐波,谐波幅值为0.2V,电压暂降开始时间为0.16s,结束时间为0.24s,暂降幅度为0.5p.u.,震荡开始时间为0.16s,结束时间为0.17s,震荡频率500Hz,幅值为0.8V,脉冲开始时间为0.25s,结束时间为0.251s幅值为1.5V,采样频率为8000Hz。HHT仿真波形如图3所示。
图3(a)中,IMF1为原始信号高频的暂态震荡和暂态脉冲分量,IMF2为叠加的5次谐波分量,IMF3为3次谐波分量,IMF4为基波的暂降分量,图3(b)、(c)为图3(a)中各个分量进行Hilbert变换得到的瞬时幅值和瞬时频率图。

(a)原始信号EEMD分解图
(b)IMF信号的Hilbert变换
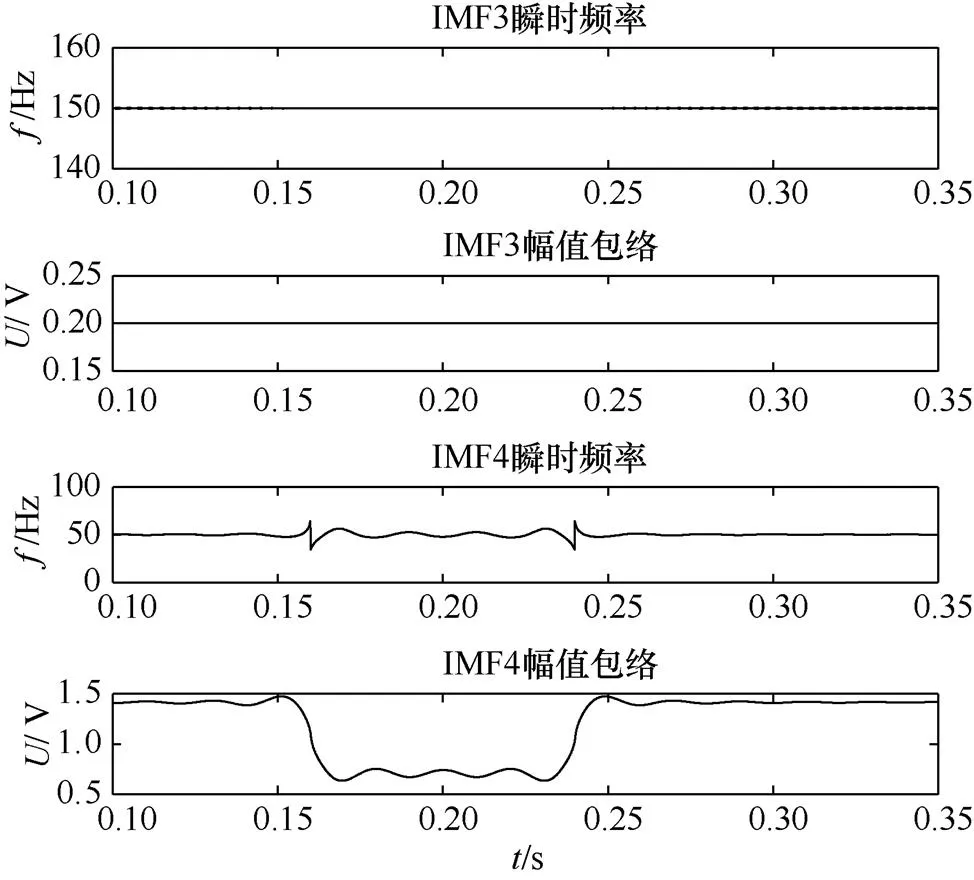
(c)IMF信号的Hilbert变换
从图3中可以确定各个扰动发生的时间,见表4。
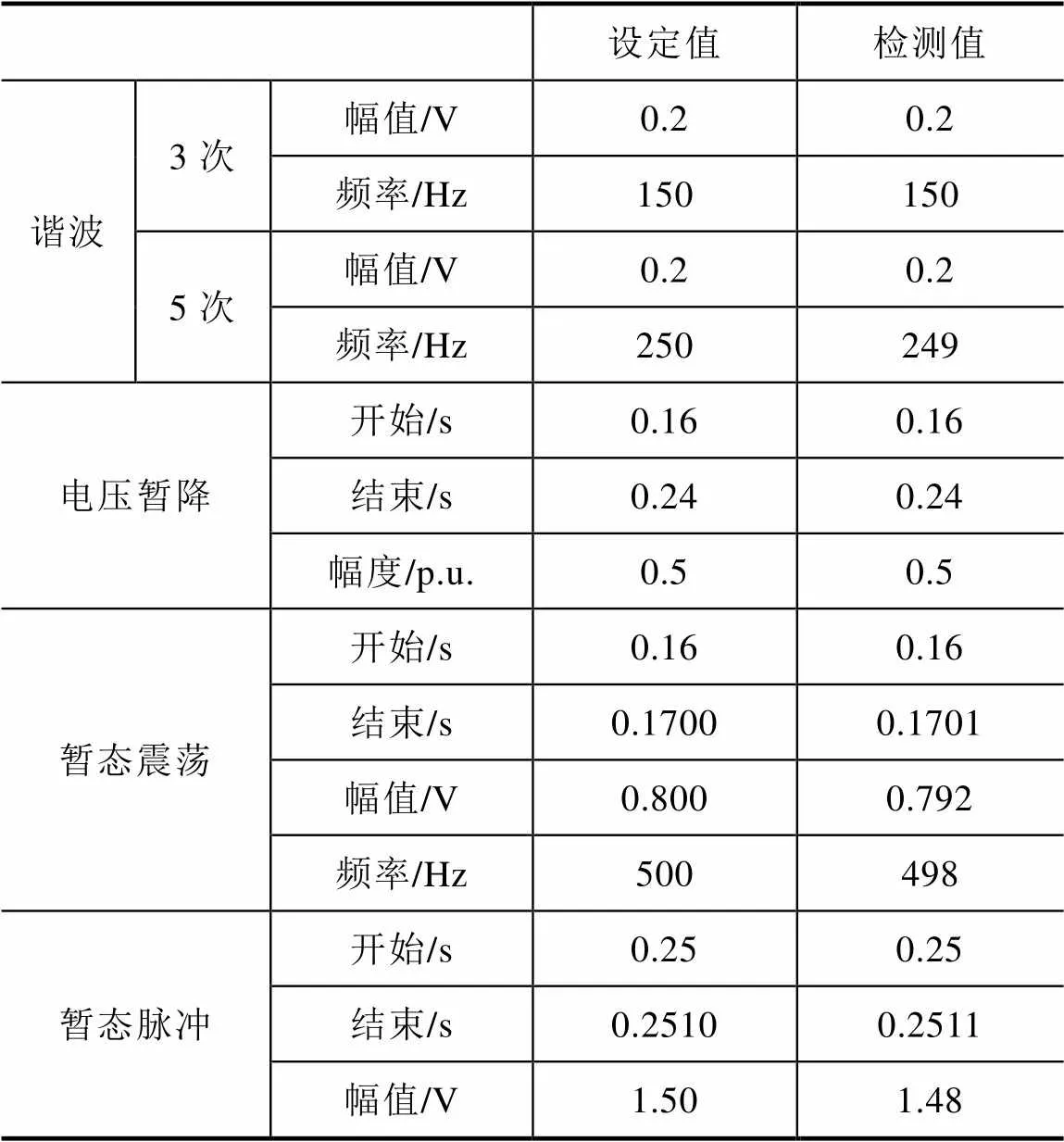
表4 谐波、暂降、暂态振荡和脉冲信号参数检测结果
分析图1、图2、图3可知,EEMD具有较好的模态分析能力,能够把每一个符合扰动特征的扰动量分离出来,实现对多扰动的有效分类。对比表2、表3、表4,本方法对电压暂降(暂升)、电压中断和谐波的检测定位误差很小,误差值刚好为一个采样间隔。而噪声的影响对暂态震荡和暂态脉冲的检测误差相对较大,但也保持在2个采样间隔内。
4 结论
本文依据电能质量多扰动信号是由基波信号与各个扰动信号叠加而成的特性,提出了用EEMD方法对多扰动信号按照特征时间尺度进行分解,并将分解得到的IMF进行Hilbert变换引入瞬时频率和瞬时幅值对扰动特征进行分析。该方法具有以下特点:
1)该方法是对传统HHT方法的改进,用于电能质量的多扰动分析中,能够有效的避免各个扰动之间的模态混叠问题。
2)通过本文对目前电网中几种最常见扰动进行叠加的仿真分析,该方法可以有效的对多扰动中包含的谐波、电压暂降(暂升)、电压中断、暂态震荡、暂态脉冲等扰动的叠加电能质量信号进行特征提取,并准确分类识别。
对电能质量多扰动的分类识别准确性并不受叠加扰动的个数影响。
[1] 王林泓, 陈学昌. 基于双密度双树小波变换的电能质量扰动识别方法[J]. 电测与仪表, 2012, 49(8): 18-21, 26.
[2] 关维国, 姚清志, 高阳, 等. 基于db4小波的配电网暂态电能质量扰动的检测与定位[J]. 电力系统保护与控制, 2015, 43(8): 102-106.
[3] 党克, 张超. 基于小波分析的谐波电流检测[J]. 电气开关, 2015, 53(6): 39-41, 45.
[4] 雷汝海, 郝震. 基于小波变换Mallat算法的电网谐波检测方法[J]. 工矿自动化, 2014, 40(12): 65-69.
[5] 徐健, 张语勍, 李彦斌, 等. 短时傅里叶变换和S变换用于检测电压暂降的对比研究[J]. 电力系统保护与控制, 2014, 42(24): 44-48.
[6] 徐永海, 赵燕. 基于短时傅里叶变换的电能质量扰动识别与采用奇异值分解的扰动时间定位[J]. 电网技术, 2011, 35(8): 174-180.
[7] 徐方维, 杨洪耕, 叶茂清, 等. 基于改进S变换的电能质量扰动分类[J]. 中国电机工程学报, 2012, 32(4): 77-84.
[8] 张志禹, 满蔚仕, 郗垒, 等. 快速S变换在电能质量分析中的应用[J]. 电网技术, 2013, 37(5): 1285-1290.
[9] 尹柏强, 何怡刚, 朱彦卿. 一种广义S变换及模糊SOM网络的电能质量多扰动检测和识别方法[J]. 中国电机工程学报, 2015, 35(4): 866-872.
[10] 李天云, 陈昌雷, 周博, 等. 奇异值分解和最小二乘支持向量机在电能质量扰动识别中的应用[J]. 中国电机工程学报, 2008, 28(34): 124-128.
[11] 杨耿煌, 温渤婴. 基于量子行为粒子群优化-人工神经网络的电能质量扰动识别[J]. 中国电机工程学报, 2008, 28(10): 123-129.
[12] 朱玲, 刘志刚, 胡巧琳, 等. 基于CWD谱峭度的暂态电能质量扰动识别[J]. 电力自动化设备, 2014, 34(2): 125-131.
[13] 陈春玲, 许童羽, 郑伟, 等. 多类分类SVM在电能质量扰动识别中的应用[J]. 电力系统保护与控制, 2010, 38(13): 74-78.
[14] 栾佳雨, 王海瑞, 毕贵红, 等. 非负矩阵分解方法识别电能质量扰动信号[J]. 计算机工程与应用, 2013, 49(4): 240-244, 253.
[15] 刘志刚, 王英, 范福强. 基于内禀模态奇异值伪熵特征提取的电能质量扰动识别[J]. 电力科学与技术学报, 2013, 28(2): 3-9.
[16] 沈跃, 张瀚文, 刘国海, 等. 基于判别字典学习的电能质量扰动识别方法[J]. 仪器仪表学报, 2015, 36(10): 2167-2173.
[17] Wu Z, Huang N E. Ensemble empirical mode decomposition-anoise-assisted data analysis method[R]. Calverton, USA: Centerfor Ocean-Land-Atmosphere Studies, 2005.
Classification and Recognition of Power Quality Multi-disturbance based on EEMD-HHT
Cao Lingzhi Liu Junfei Zheng Xiaowan
(Zhengzhou University of Light Industry, Zhengzhou 450002)
For the reason that existing classification and recognition methods of power quality multi-disturbance have lower classification accuracy and recognition ability, the EEMD-HHT method is introduced to classifying the power quality multi-disturbance, which is based on the characteristics of power quality multi-disturbance. Firstly, the signal was decomposed into Intrinsic Mode Function (IMF) by the EEMD. Then the noise in the components is suppressed through thresholding and reconstructing each IMF with adaptive thresholds. Finally, the instantaneous attributes and start-stop time of the power quality multi-disturbance signals can be extracted with Hilbert transform. Simulation results in matlab show that the proposed method can effectively detect, locate and analyze power quality multi- disturbance.
power quality multi-disturbances; hilbert huang transform; ensemble empirical mode decomposition
曹玲芝(1965-),女,教授,硕士生导师,从事网络化测试技术、非线性控制理论应用方面的研究开发工作。
