基于特征值分析法的电力系统次同步振荡研究

于云霞 李 娟



基于特征值分析法的电力系统次同步振荡研究

于云霞 李 娟

（北京信息科技大学自动化学院，北京 100192）

本文以基准模型为研究对象，利用特征值分析法对电力系统次同步振荡问题进行了深入的分析，计算得到了次同步振荡的频率和阻尼参数等，进一步用特征值分析法计算了系统的参数的改变对于次同步振荡阻尼的影响，通过仿真验证了特征值分析算法的正确性。

次同步振荡；特征值分析法；电气参数；状态空间方程

次同步振荡一般发生在具有串联电容补偿的电力系统，高压交直流输电系统、电力系统稳定器或者静止无功补偿装置的控制设备等也可能引起这种振荡。这是由于在特定条件下，大型汽轮发电机组的转子轴系具有弹性，又因为机械和电气的相互作用引发振荡，从而使整个电力系统运行不稳定[1]。现在特征值分析法已被广泛用于线性系统的分析，文献[2]中通过计算特征值分析了串补电容对次同步振荡产生的影响。文献[3]分析了基于特征值法的次同步阻尼守恒特性。文献[4]介绍了20阶和27阶系统的特征值分析结果与以前文献分析结果的误差。文献[5]通过求取最小特征值的灵敏度来分析对静态电压稳定的影响。上述文献都有效的利用了特征值的特性分析了对系统稳定性的影响，但是对于计算特征值的状态方程的推导结果方面介绍甚少，以及改变电气参数分析对次同步振荡的影响，此方面的文献鲜见。故文章对这两方面做了详细的研究，用PSCAD仿真验证了算法的有效性。

1 次同步振荡的产生机理

当有串补电容的电力系统在某一稳态运行情况下，发电机轴系有一个小的扰动，该扰动会在发电机的定子中产生次同步频率为（1-m）与超同步频率为（1+m）的电压分量。定子回路中电感与电容的谐振频率都是（1-m）时，定子回路中频率为（1-m）的电流分量与频率为（1+m）的电压分量同相位，三相次同步电流将会于空间中形成一个转速大小是（1-m）的旋转磁场，该磁场产生的电磁转矩将会对轴系频率为m的振荡分量呈负阻尼作用，当电气谐振频率同发电机轴系自然频率互补时，串补电路产生最大的负阻尼，进而引发次同步振荡。与之相关的内容包括以下几方面。

1）感应发电机效应的实质是由于同步发电机的转子对于低于系统同步频率的次同步频率电流表现为视在负电阻特性[6]。由计算可知流入电枢端部的次同步频率的电流所遇到的等效发电机电阻与转子电阻值和转差率有关，并且是一个负值，当转差率减小时，电阻的绝对值增大。当这个电阻的绝对值比该频率下电枢绕组和网络的电阻之和大的时候，电枢绕组中的次同步频率电流持续存在，甚至增大，形成感应发电机效应。

2）扭转相互作用是指电力系统中串联电容补偿电网与汽轮发电机的机械系统之间的相互作用[7]，这种作用与电气系统和机械系统的动态特性都有联系。电气系统与机械系统之间的相互激励作用就叫扭转相互作用。

3）暂态力矩放大作用是指系统有干扰时，电磁转矩施加于发电机转子上，使发电机轴段承受转矩压力。简而言之，暂态转矩方法效应是由于电气和机械自然频率之间的振荡引起的。

2 特征值分析法的状态空间方程推导

2.1 特征值分析法的原理

特征值分析法是在小扰动情况下，获得系统元件的线性化模型，利用求解的特征值来判断系统稳定性的一种方法[8]。

2.2 研究模型

以IEEE第一基准模型为例建立状态空间方程，研究模型如图1所示。系统额定工频电气角速度为b=2pN（N=60Hz）文中出现的各量均为标幺值，单位为p.u.。下标为0的代表稳态值，基准值的选取见文献[1]。详细参数见文献[9]。系统的初始运行状态：发电机端电压为1.05p.u.，发出的有功功率为0.9p.u.，功率因数为0.9。

图1 IEEE第一基准模型系统接线图

文献[9]详细推导了特征值分析法的状态方程，尤其是对电磁回路模型的推导较缜密，给出了状态方程的由来。由20个状态量组成的全系统的状态向量为

（1）

2.3 发电机组轴系模型

典型的大型汽轮发电机轴系一般采用六质量块-弹簧模型，即高压缸（HP），中压缸（IP），低压缸（LPA和LPB），发电机（GEN）和励磁机（EXC）。由线性化方程[2]推导出的系数矩阵如式（2）所示。

式中，为转子轴系各质量块的惯性时间常数；和分别为弹性系数和阻尼系数。

2.4 发电机电磁回路模型

发电机电磁回路使用完整的6绕组模型，其磁链和电压平衡方程如式（3）至式（6）所示[10]。

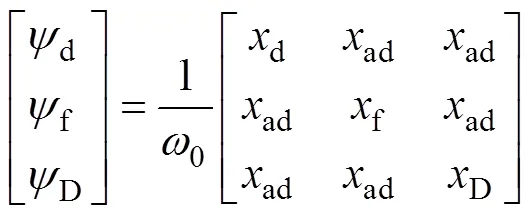
（4）

（5）

在式（3）和式（4）中，0=1。

由式（5）和式（6）的磁链方程和电压平衡方程得到发电机的6个绕组线性化微分方程，如式（7）所示。

则由式（7）推导出系数矩阵计算如式（8）至式（10）所示。

（9）

（10）

同时由式（7）可得出发电机轴系对于电磁回路的系数矩阵，如式（11）所示。

2.5 串补电路模型

串补电路由线性化方程[2]推导出的系数矩阵如式（12）至式（14）所示。

（13）

（14）

同时可以得出：电磁回路对于串补电路的系数矩阵如式（15）所示。

式中，为工频下变压器电抗T与线路电抗L之和。

3 特征值分析结果

3.1 特征值计算结果

在串补度不同的条件下，分析特征值分析法的计算结果。当串补电容为47.09mF时，则串补度，结果为0.3。当串补电容值为30.75mF时，串补度则为0.5。系统的特征值有20个，选取代表低频和次同步振荡频率的部分特征值计算结果见表1。

表1 特征值计算结果

由表1可以看出，在系统的6个机械系统振荡模式中，5个振荡模式对应于轴系质量块之间的扭振。表中串补度为0.3时的特征值实部为1.21，表明主要振荡频率是32.25Hz，且串补度为0.5时的特征值实部为0.28，表明主要的振荡频率为25.5Hz。依次与扭振模式Mode4与Mode3对应。下文通过仿真分析验证了特征值计算结果的正确性。

3.2 仿真结果

仿真模型为PSCAD中的ieee_ssr_bench模型，仿真时间为20s。然后在仿真结果给出的数据基础上，利用Matlab编程分析得到仿真结果。当串补度分别为0.3和0.5时，仿真结果如图2和图3所示。

由图2和图3可以看出，在1.5s发生短路故障以后，发电机转速差不是保持为零，出现了幅值振荡，并且幅值不断增大，这说明，在发生故障以后，系统已经不再稳定，发生了次同步振荡，与特征值分析法的结果一致。

图2 发电机转速差时域波形图

图3 发电机转速差时域波形图

然后在PSCAD仿真结果的基础上，以转速差为输出信号，用Matlab分析串补度不同时的频谱如图4和图5所示。

由图4和图5可以看出，串补度为0.3时，振荡频率为15.75Hz、20.25Hz、25.5Hz、32.25Hz，其中频率为32.25Hz的频谱幅值较大。串补度为0.5时，振荡频率为15.75Hz、20.25Hz、25.5Hz、32.25Hz，其中频率为25.5Hz的频谱幅值较大。这与特征值分析法的结果一致。

图4 串补度为0.3的发电机转速差频谱分布

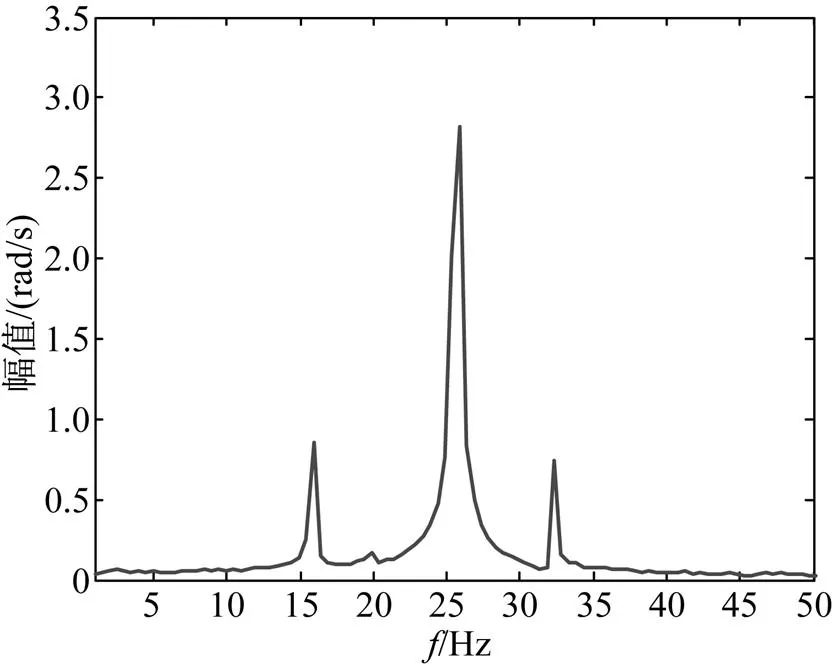
图5 串补度为0.5的发电机转速差频谱分布

扭振模态阻尼是轴系在扭振频率下扭振时，其扭振衰减速率的量化表示。去掉滤波失真之后的幅值包络线的最小二乘拟合直线如图6和图7所示。

图6 模式3转速差幅值包络拟合直线

图7 模式4转速差幅值包络拟合直线

由图6和图7可以计算出，模式3的衰减因子是0.29，模式4的衰减因子是1.22。与特征值分析法的结果一致。

4 电气参数变化对次同步振荡的影响

理论上，对于一个具体的串联电容补偿输电系统，其内部的参数影响着次同步频率范围内的能量交换，进而影响次同步振荡特性，因此，在特征值分析法的基础上研究这些参数对次同步振荡的影响效果具有非常重要的意义。将励磁绕组漏电抗f和定子a相绕组的电阻a分别从降低50%到提高50%分析对系统次同步振荡的影响，特征值分析结果如图8和图9所示。

图8 xf变化对应扭振模式的阻尼

图9 ra变化对应扭振模式的阻尼

由图8可以看出：模式3的特征值实部下降了3.2%，表明对应阻尼增加，负阻尼减小；模式4的特征值实部下降了3.6%，表明对应阻尼增加，负阻尼减小。

由图9可以看出：模式3和模式4的特征值实部几乎没有变化，说明a的变化对次同步振荡的影响很小，可以忽略。这是由于其值远远小于线路阻抗，对振荡模式的影响很小。

5 结论

本文详细列出了状态方程的推导结果，对今后的研究有基础性的意义。利用PSCAD仿真和Matlab编程验证了算法的正确性。在此基础上，根据特征值的计算结果改变参数后进行仿真研究，发现f对次同步振荡影响相对要明显一些，而电阻a对次同步振荡的影响相对较弱。这是由于机组电阻在系统总体电阻中的占比很小的缘故。在今后的工作中可以利用特征值分析法研究不同的机组电抗对次同步振荡的影响程度，便于在实际工程中通过预先的设计调整参数，为降低次同步振荡的风险提供条件。

[1] 肖湘宁, 郭春林, 高本峰, 等. 电力系统次同步振荡及其抑制方法[M]. 北京: 机械工业出版社, 2014.

[2] 孙丽平. 基于特征值分析法的具有固定串联补偿的电力系统次同步谐振分析[D]. 武汉: 武汉大学, 2003.

[3] 肖湘宁, 杨琳, 张丹, 等. 基于特征值法的次同步阻尼守恒特性分析[J]. 电网技术, 2011, 35(11): 80-84.

[4] 李道霖, 张双平. 基于特征值分析法的电力系统稳定性研究[J]. 沈阳工程学院学报(自然科学版), 2010, 6(4): 326-329.

[5] 王均衡. 采用最小特征值灵敏度法改善静态电压稳定性[D]. 郑州: 郑州大学, 2014.

[6] 栗然, 卢云, 刘会兰, 等. 双馈风电场经串补并网引起次同步振荡机理分析[J]. 电网技术, 2013, 37(11): 3073-3079.

[7] 孔永乐. 大规模风电外送次同步振荡机理研究[D]. 北京: 华北电力大学:北京华北电力大学, 2013.

[8] Uchida N, Nagao T. A new eigen-analysis method of steady-state stability studies for large power systems:A matrix method[J]. IEEE Transactions on Power Systems, 1988, 3(2): 706-714.

[9] IEEE Subsynchorous Resonance Woking Group. First benchmark model for computer simulation of subsynchronous resonance[J]. IEEE Transactions on Power Apparatus and Systems, 1977, PAS-96(5): 1565-1572.

[10] 陈萌. 复杂电力系统次同步振荡问题特征值分析的建模与算法研究[D]. 武汉: 华中科技大学, 2013.

The Power System Subsynchronous Oscillations were Studies based on Eigenvalue Analysis

Yu Yunxia Li Juan

(School of Automation, Beijing Information Science and Technology University, Beijing 100192)

This paper taked the benchmark model as the research object, and used eigenvalue analysis method to analyze the subsynchronous oscillation of power system deeply. The frequency and damping parameters of subsynchronous oscillation were calculated. Furthermore, the eigenvalue analysis method was used to calculate the change of the parameters of the system for the influence of subsynchronous oscillation damping. The correctness of the eigenvalue analysis algorithm was verified by simulation.

subsynchronous oscillation; eigenvalue analysis method;electrical parameters; the state space equation

国家自然科学基金项目（51477010）

于云霞（1990-），女，硕士研究生，研究方向为电力系统次同步振荡分析及抑制。