基于核磁共振T2谱集中度的低孔隙度低渗透率储层饱和度参数研究
2017-04-25丁娱娇柴细元邵维志李俊国韩艳李庆合
丁娱娇, 柴细元, 邵维志, 李俊国, 韩艳, 李庆合
(1.中国石油渤海钻探工程有限公司测井分公司, 天津 300280; 2.大港油田分公司勘探开发研究院, 天津 300280; 3.大港油田分公司第二采油厂, 天津 300280)
0 引 言
利用测井技术定量评价低孔隙度低渗透率储集层含油饱和度,前人在实践中针对不同的储集层条件研究和发展了一系列的变形阿尔奇公式,以解决实际中存在的难题。Givens、Crane、曾文冲等都给出了考虑微孔隙水导电的解释模型,李宁模型不仅考虑了储层复杂孔隙结构对饱和度模型的影响,而且考虑了油层与气层的差异[1-2]。但是,模型中都存在很难确定的参数,应用推广比较困难,在现场生产解释中使用最多的还是阿尔奇公式。针对歧口凹陷中深层低孔隙度低渗透率储层,迟秀荣等[3]对阿尔奇公式在该地区的适应性作出了详细的分析,认为该地区地层因素与孔隙度关系以及电阻率增大率与饱和度关系仍然遵从阿尔奇公式的基本关系式。由于沉积环境和成岩作用的复杂性,导致孔隙结构复杂、储层非均质性强,常规实验室得到的不同岩样的胶结指数m、饱和度指数n值均存在明显差异,其中m变化范围为1.0~2.5,n变化范围为1~6;对于低孔隙度低渗透率储层,饱和度参数m、n的变化对饱和度计算结果影响非常大[4],区域平均m、n值已经满足不了低孔隙度低渗透率储层饱和度评价。获得准确的m、n参数成为低孔隙度低渗透率储层饱和度定量评价的关键。
本文在总结前人m、n参数主控因素分析基础上,通过综合分析300余块次岩样的岩电参数发现,岩样m、n值受孔隙度、地层水电阻率、孔隙结构特征形态等因素共同制约。在主控因素分析基础上,提出了核磁共振T2谱集中度概念反映微观孔隙结构分布形态,分不同地层水电阻率范围,建立利用核磁共振T2谱集中度计算饱和度关键参数m、n的解释模型,获得连续的、反映储层物性变化的m、n值,有效提高了m、n参数计算准确性。
1 饱和度参数m、n主控因素分析
贾自力等[5]从沉积和成岩作用过程分析了阿尔奇公式中m、n参数的影响因素,认为不同成岩阶段,m、n参数值不同;李梅等[6]认为m值主要受储集空间类型和泥质分布形式影响;毛志强等[7]认为水膜厚度、孔隙联通性、喉道大小、孔隙半径均值等均影响n值的变化;张明禄等[8]认为储集空间类型是影响m、n参数的主要因素;李秋实等[9]文饱和度指数n值主要受储层孔喉比的影响。总之,m、n参数与岩性、物性、孔隙结构及成岩作用等有关,是地下地质体的综合响应。本文以歧口凹陷中深层低孔隙度低渗透率岩心为基础,综合分析地层水电阻率、物性、岩性等对m、n参数的制约作用。
1.1 地层水电阻率对m、n参数的影响
为认识地层水电阻率是否影响m、n参数,选取不同孔隙度岩样开展变地层水电阻率环境下m、n参数测量,每块岩样在饱和地层水矿化度分别为8 000、12 000、16 000、20 000、30 000 mg/L,室温20 ℃条件下地层水电阻率分别为0.68、0.47、0.38、0.29、0.2 Ω·m等5种环境下测量其地层因素—孔隙度、电阻率增大率—饱和度,得到每块岩样不同地层电阻率下m、n值。地层水电阻率对m、n值有明显影响,随着地层水电阻率增加,m、n呈降低的趋势,但并不是简单的线性变化,地层水电阻率大于0.29 Ω·m,地层水电阻率对m、n值影响明显;当地层水电阻率小于0.29 Ω·m,地层水电阻率对m、n影响变缓。不同孔隙度条件下,地层水电阻率对m、n影响程度不同,地层水电阻率对m值的影响随着物性变好而增大,对n值的影响随着物性变好而降低。因此,建立m、n参数计算模型必须考虑地层水电阻率的影响。
1.2 物性对m、n参数的影响
物性对m、n参数的影响主要考虑储层孔隙度和微观孔隙结构特征2个方面。描述储层微观孔隙结构特征的方法有2种,分别为毛细管压力测量法和核磁共振测量法[10]。考虑到后续方法建立的实用性,本文选择核磁共振标准T2谱作为微观孔隙结构表征方法。图1展示了6块粉砂质细砂岩岩样的核磁共振标准T2谱分布,该6块岩样在进行饱和水核磁共振测量和m、n测量时饱和的地层水电阻率均为0.38 Ω·m。图1(a)的3块岩样T2谱位置和形态基本一致,代表3块岩样微观孔隙结构很相似,3块岩样T2谱孔隙度分量幅度和包络面积不同,说明3块岩样孔隙度不同。在岩性、地层水电阻率、微观孔隙结构均基本一致的情况下由于孔隙度的差异,使得3块岩样的m、n值存在明显差异,说明孔隙度的变化影响m、n值的变化。图1(b)的3块岩样T2谱位置和形态存在差异,但是包络面积相同,说明3块岩样孔隙度相同,但微观孔隙结构存在差异。在岩性、地层水电阻率、孔隙度均基本一致的情况下由于微观孔隙结构的差异,使得3块岩样的m、n值存在明显差异,说明微观孔隙结构的变化影响m、n值的变化。

图2 不同骨架颗粒岩样m、n值以及核磁共振标准T2谱
通常应用核磁共振T2谱的几何平均值描述储层微观孔隙结构的变化[8],T2几何平均值越大说明储层以大孔径为主,T2几何平均值越小说明储层以小孔径为主。m值随着孔隙度、T2几何平均值增加而增加;n值随着孔隙度、T2几何平均值增加而降低,说明物性越差m值越小,n值越大。
1.3 岩性对m、n的影响
歧口凹陷低孔隙度低渗透率储层岩性主要为砂泥岩储层,分析岩性对m、n的影响,主要是分析骨架颗粒大小对m、n的影响。图2展示了不同骨架颗粒岩样的m、n值和核磁共振标准T2谱分布情况。从图2(a)可见,骨架颗粒的大小在一定程度上影响m值的变化,在相同孔隙度条件下,含砾不等粒砂岩的m值要大于细砂岩和粉砂岩;图2(b)展示了不同骨架颗粒n值,可见n值与骨架颗粒变化规律不是很明显,难以明确地描述骨架颗粒对n值的影响;图2(c)展示了不同骨架颗粒岩样的核磁共振标准T2谱分布,可见不同骨架颗粒岩样其核磁共振标准T2谱分布位置明显不同,骨架颗粒越细,T2谱分布越靠左,骨架颗粒越粗,T2谱分布越靠右,骨架颗粒粒径越复杂,T2谱展布位置越宽,说明骨架颗粒不同,微观孔隙结构不同。故岩性对m、n值的影响,可以归结到微观孔隙结构对m、n值的影响。
1.4 阳离子交换容量QV对m、n的影响
通过实验室阳离子交换量测试发现,歧口凹陷中深层低孔隙度低渗透率储层阳离子交换容量QV值均在2 meq/mL之内,绝大部分数值在0.8 meq/mL之内。当QV<0.8 meq/mL,QV的变化对m影响不明显;当QV>0.8 meq/mL,随着QV的增加,m值降低。QV对n影响明显,随着QV增加n值降低。随着泥质含量增加QV增加,可以用泥质含量表征储层QV含量。在测井计算中,除了利用常规岩性测井曲线描述储层泥质含量以外,核磁共振测井T2谱位置是一种非常有效的泥质含量指示方法,黏土束缚流体部分T2谱幅度越高代表泥质含量越高,黏土束缚流体部分T2谱幅度越低代表泥质含量越低。黏土束缚流体部分T2谱分布形态不同代表储层微观孔隙结构存在差异,故阳离子交换容量QV对m、n的影响同样可以归结到微观孔隙结构对m、n值的影响。
通过岩石润湿性实验测量分析可知,歧口凹陷储层岩石润湿性整体表现为亲水性,可以不考虑润湿性变化对m、n值的影响。歧口凹陷中深层低孔隙度低渗透率储层影响m、n值的主要因素有地层水电阻率、孔隙度、微观孔隙结构。

图3 不同T2谱集中度岩样核磁共振标准T2谱
2 基于T2谱集中度的饱和度关键参数计算
2.1 T2谱集中度概念的提出
利用核磁共振描述储层孔隙结构最常用的方法是利用T2几何平均值表征,但是针对歧口凹陷中深层低孔隙度低渗透率储层,低孔隙度低渗透率储层其沉积环境和成岩作用的复杂性,造成其孔隙结构与常规储集层存在很大的差异,基于T2几何平均值表征孔隙结构描述微观孔隙结构对m、n值的影响已经满足不了m、n参数评价的需求。图3(a)为2块岩样的核磁共振T2谱分布,2块岩样孔隙度、T2几何平均值均一致,但是其测量得到的m、n值差别却很大,特别是n值,从1.14变化到1.87,说明简单的T2几何平均值表征孔隙结构的方法已经满足不了m、n值评价的需求,亟需能够充分考虑孔径分布形态和不同孔径尺寸搭配关系的孔隙结构表征参数的方法描述微观孔隙结构的变化。
根据分析,为提高复杂孔隙结构低孔隙度低渗透率储层饱和度关键参数m、n值的计算准确性,需要提出一个能够充分考虑T2分布形态、着重研究不同大小的孔隙搭配关系的微观孔隙结构特征表征参数。为此,引入气象学研究中评价空间气旋或者风暴、云分布所常用的集中程度函数[11],它可以用来定量指示物理场或函数在空间分布的集中程度,称为分布模型,其数学表达式为
ψ=
(1)
式中,ψ为核磁共振T2谱集中度,ψ值无量纲、归一化,数值范围0~1。ψ值大小反应T2谱分布形态,ψ值越小,反映T2谱的集中程度越小,T2谱分布越发散,代表各种尺寸孔径均有,孔隙结构越复杂;ψ值越大,说明T2值越集中,T2谱形态越规则且以单一的孔径尺寸为主,储层孔隙结构越规则。N为核磁共振T2谱时间刻度区间的个数;i为第i个区间φ为核磁共振孔隙度;T2g为核磁共振T2谱的几何平均值;φ2g为T2几何平均值分布区间相对应的孔隙度分量;T2i为第i个区间的T2谱对应时间刻度;φ2i为T2i区间相对应的孔隙度分量。
有了T2谱集中度参数就很好回答图3(a)中2块岩样m、n参数为什么会出现如此大差异的原因,虽然2块岩样的孔隙度、T2几何平均值均一样,但是2块岩样的T2谱集中度ψ值却存在明显差异,说明微观孔尺寸分布特征存在一定程度差异,随着ψ值降低,m值降低,n值增大。图3(b)为2块孔隙度、孔隙结构基本一致岩样核磁共振T2谱分布,可见两块岩样的微观孔隙结构特征非常接近,其孔隙度、T2几何平均值、T2谱集中度基本一致,最终测量得到的m、n值也基本一致,说明将T2谱集中度与T2几何平均值相结合可以更好地描述微观孔隙结构分布特征对m、n值的影响。
2.2 饱和度关键参数计算模型的建立
歧口凹陷中深层低孔隙度低渗透率储层饱和度关键参数m、n受地层水电阻率、孔隙度、微观孔隙结构特征共同制约,储层微观孔隙结构特征可以由核磁共振T2几何平均值和T2谱集中度共同描述,其中T2几何平均值表征孔径尺寸大小,T2谱集中度表征孔径尺寸分布形态。因此,可以建立地层水电阻率、孔隙度、T2几何平均值、T2谱集中度加权组合的m、n计算模型。
首先对孔隙度、T2几何平均值、T2谱集中度加权组合,定义为储层微尺度特征参数,计算公式为
(2)
微尺度特征参数主要用于描述储层微观孔隙结构特征,微尺度特征参数越大,说明储层物性越好,微观孔隙结构分布越均匀;微尺度特征参数越小,说明储层物性越差,微观孔隙结构分布非均质性越强。在获得储层微尺度特征参数基础上,分地层水电阻率建立不同地层水电阻率范围的m、n与微尺度特征参数之间关系(见图4),得到m、n计算公式为
当Rw≤0.3 Ω·m时
m=0.6052·χ+1.2894R2=0.93
(3)
n=4.56·χ2-10·χ+7.34
R2=0.89
(4)
当0.3 Ω·m m=0.5065·χ+1.2106R2=0.90 (5) n=3.71·χ2-7.88·χ+5.723 R2=0.91 (6) 当Rw≥0.5 Ω·m时 m=0.4234·χ+1.14R2=0.88 (7) n=2.3483·χ2-4.4758·χ+3.58 R2=0.83 (8) 图5为不同方法计算m、n值与岩心分析m、n值的对比图。图5中蓝色圆点为综合考虑地层水矿度、孔隙度、T2几何平均值建立的计算模型得到的m、n值与岩心分析对比,黄色菱形点子为本文提出的微尺度特征参数计算得到的m、n值与岩心分析对比。由图5可见,在增加考虑T2谱集中度因素之后的m、n计算结果与岩心分析结果的一致性要远好于未考虑T2谱集中度因素的计算模型。其中,m值平均相对误差降低到2.1%,n值平均相对误差降低到7.23%,有效提高了m、n参数计算精度。 图4 不同地层水电阻率环境下微尺度特征参数与m、n关系图 图5 计算m、n与岩心分析m、n对比图 图6为歧北斜坡区某井主力油层滨Ⅳ油组应用实例。图6中第5道为核磁共振测井标准T2谱和T2几何平均值,第6道为T2谱集中度,第7道为基于储层微尺度特征参数计算得到的m值与岩心分析的m值对比,第8道为计算n与岩心分析n值对比,第9道为总含水饱和度与束缚水饱和度。由图6可见,本文所述方法计算得到的m、n与岩心分析m、n的一致性非常好,说明该方法应用效果很好。由该方法计算得到的总含水饱和度与核磁共振测井提供的束缚水饱和度在有些井段差异较大,说明该段储层含油不饱满,物性相对较好的层段含油丰度高,物性较差的层段含油丰度低,有产水的可能。对图6中井段试油,压后日产油15 m3,水11 m3,试油结论为油水同层,验证了解释结论的正确性。 图6 歧口凹陷某低孔隙度低渗透率储层饱和度计算应用实例 图7 沧东凹陷某低孔隙度低渗透率储层饱和度计算应用实例 (1) 低孔隙度低渗透率储层饱和度关键参数m、n值受孔隙度、地层水电阻率、孔隙结构特征形态等因素共同制约,计算m、n值必须综合考虑以上因素影响。 (2) 提出了利用核磁共振T2几何平均值和T2谱集中度共同描述储层微观孔隙结构特征的方法,其中T2几何平均值表征孔径尺寸大小,T2谱集中度表征孔径尺寸分布形态。 (3) 在此基础上,分地层水电阻率建立了孔隙度、T2几何平均值、T2谱集中度加权组合的m、n计算模型,利用模型建立的m、n值进行含油饱和度计算,在实际应用中取得良好应用效果。 参考文献: [1] 曾文冲. 油气藏储集层测井评价技术 [M]. 北京: 石油工业出版社, 1991. [2] 孙建孟, 王克文, 李伟. 测井饱和度解释模型发展及分析 [J]. 石油勘探与开发, 2008, 35(1): 101-107. [3] 迟秀荣, 邵维志, 丁娱娇, 等. 歧口凹陷复杂砂岩储层饱和度计算方法探讨 [J]. 测井技术, 2011, 35(3): 6-31. [4] 张振城, 孙建孟, 马建海, 等. 阿尔奇公式中a、m对饱和度计算结果的影响 [J]. 石油大学学报(自然科学版), 2004, 18(6): 27-34. [5] 贾自力, 陈文武, 房育金, 等. 低孔隙度低渗透率泥质砂岩储层中胶结指数m和饱和度指数n的计算和应用 [J]. 测井技术, 2010, 34(2): 108-114. [6] 李梅, 陈红兵, 黄小平, 等. 用岩石导电效率理论来说明低孔隙度低渗透率储层孔隙结构对m指数的影响 [J]. 内蒙古石油化工, 2007, 1: 112-114. [7] 毛志强, 高楚桥. 孔隙结构与含油岩石电阻率性质理论模拟研究 [J]. 石油勘探与开发, 2000, 27(2): 87-90. [8] 张明禄, 石玉江. 复杂孔隙结构砂岩储层岩电参数研究 [J]. 石油物探, 2005, 44(1): 21-28. [9] 李秋实, 周荣安, 张金功, 等. 阿尔奇公式与储层孔隙结构的关系 [J]. 石油与天然气地质, 2002, 23(4): 364-367. [10] 李天降, 李子丰, 赵彦超, 等. 核磁共振与压汞法的孔隙结构一致性研究 [J]. 天然气工业, 2006, 26(10): 57-59. [11] 李潮流, 徐秋贞, 张振波. 用核磁共振测井评价特低渗透砂岩储层渗透性新方法 [J]. 测井技术, 2009, 33(5): 436-439.

3 应用实例分析

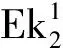

4 结 论
