低孔隙度低渗透率储层弯曲波影响因素分析及渗透率反演

2017-04-25许孝凯范宜仁翟勇王胜利刘美杰

测井技术 2017年4期

许孝凯, 范宜仁, 翟勇, 王胜利, 刘美杰

(1.中石化胜利石油工程有限公司测井公司, 山东东营 257096; 2.中国石油大学(华东), 山东青岛 266580;3.中国石油吉林油田分公司勘探开发研究院, 吉林松原 138000)

0 引言

现今有多种手段获取储层的渗透率,其中包括岩心分析渗透率、核磁共振测井解释渗透率、常规测井方法解释渗透率以及斯通利波渗透率。利用弯曲波衰减曲线反演渗透率的思想也较早被提出[1],并且利用弯曲波反演渗透率的可行性以及反演方法也有文献进行了系统的论述[2]和误差分析[3]。利用弯曲波衰减反演渗透率方法处理实际数据和通过横向各向同性地层模型反演的地层水平方向和垂直方向渗透率分析渗透率各向异性[4-5]的工作也已经开展。利用弯曲波频移进行渗透率反演也取得了一定成果[6-7]。本文在此基础上,综合分析了弯曲波影响因素,并给出了一种新的利用弯曲波频移进行渗透率反演的方法,通过对实际资料进行处理,取得了较好的应用效果。

1 理论基础

1.1 均匀孔隙地层的测井声波传播理论

研究的体系为径向半无限的Biot双相介质包围的流体井孔,井内流体密度为ρf,声速为vf,井孔半径为a,井外双相介质的骨架是由各向同性的密度为ρs、体变模量为Ks的固体颗粒固结构成,骨架孔隙度为φ,平均弹性常数为λb和μb(或Kb),渗透率为K,孔隙内流体的密度和声速分别为ρf和vf(体变模量Kf),动力黏滞系数为η。

以井轴为z轴建立柱坐标系(r,θ,z),n级多极源置于z轴原点且处于xy平面内,得到井孔内流体的位移势函数

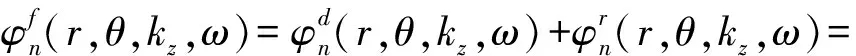
(1)

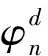
根据Biot理论,井孔外孔隙介质中的声场可以用骨架的位移u和渗流位移w表示,n极声源产生的2个位移场可以用位移位表示为

un=φn+×

(2)

ωn=×

(3)

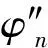
利用实轴积分方法,可以得到井孔中时域(广义)声压波形

(4)

式中,V0(ω)是声源的频谱。

(5)

1.2 影响因素分析

为更好地利用弯曲波得到地层渗透率信息,对影响弯曲波相速度和衰减的多种因素进行了灵敏度分析。响应模型对参数p的灵敏度定义表达式为

(6)

式中,vphase(ω)是模式波相速度;Q为衰减因子。

(1) 硬地层。图1为硬地层条件下弯曲波相速度和衰减对井孔流体声速、井眼大小、地层横波速度和渗透率的灵敏度。其中地层渗透率为1 mD*非法定计量单位,1 mD=9.87×10-4 μm2,下同。由图1可知,弯曲波相速度和衰减对渗透率的灵敏度较其他因素较小,且相速度对渗透率的灵敏度要小于衰减对渗透率的灵敏度,这种现象同样更明显地存在于软地层中(见图3)。这也说明了利用弯曲波衰减提取地层渗透率的可靠性。图2为不同渗透率地层中,弯曲波相速度和衰减对渗透率的灵敏度。由图2可知,地层渗透率不同时,灵敏度大小也不同;渗透率越大,弯曲波对渗透率的灵敏度越大,这也从理论上说明了渗透性越好,反演效果也会越好。

(2) 软地层。图3为软地层中弯曲波相速度和衰减对井孔流体声速、井眼大小、地层横波速度和渗透率的灵敏度。对应地层渗透率为1 mD。灵敏度随频率的变化趋势和硬地层下趋势是一致的。

综上所述,弯曲波速度和衰减受地层渗透率、弹性性质、井眼大小以及井孔流体性质等多因素影响,利用弯曲波处理求取地层渗透率时,需要将渗透率外的其他影响因素排除。与硬地层相比,软地层中井眼和仪器半径以及井孔流体声速对弯曲波灵敏度降低。所以,从这方面考虑,对软地层利用弯曲波反演渗透率更有优势。

1.3 孔渗条件对弯曲波中心频率影响

数值计算时选取的地层和井孔参数见表1。

波的中心频率由式(7)计算

(7)

式中,f为频率;W(f)为波的波谱。

从图5、图6中可以看出,在偶极情况下,弯曲波中心频率均随着渗透率和孔隙度的增加而降低。图5中,在偶极3 kHz时,弯曲波中心频率由渗透率为0.1 mD、孔隙度为5%时的5.35 kHz,下降到渗透率为100 mD、孔隙度为20%时的4.7 kHz,降幅为0.65 kHz。图6中,在偶极5 kHz时,弯曲波中心频率由渗透率为0.1 mD、孔隙度为5%时的6.38 kHz,下降到渗透率为100 mD、孔隙度为20%时的5.8 kHz,降幅为0.58 kHz,且随着渗透率的增大,中心频率单调减小。对弯曲波,其中心频率随渗透率的增加均有一定程度的减小,由弯曲波全波波形可知,弯曲波波形成分较纯净。因此,利用弯曲波的频移反演渗透率也是可行的。

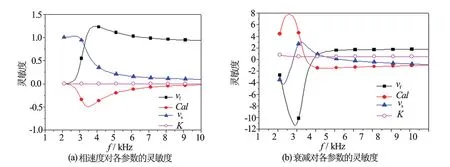
图1 弯曲波速度与衰减对硬地层不同参数的灵敏度(渗透率为1 mD)

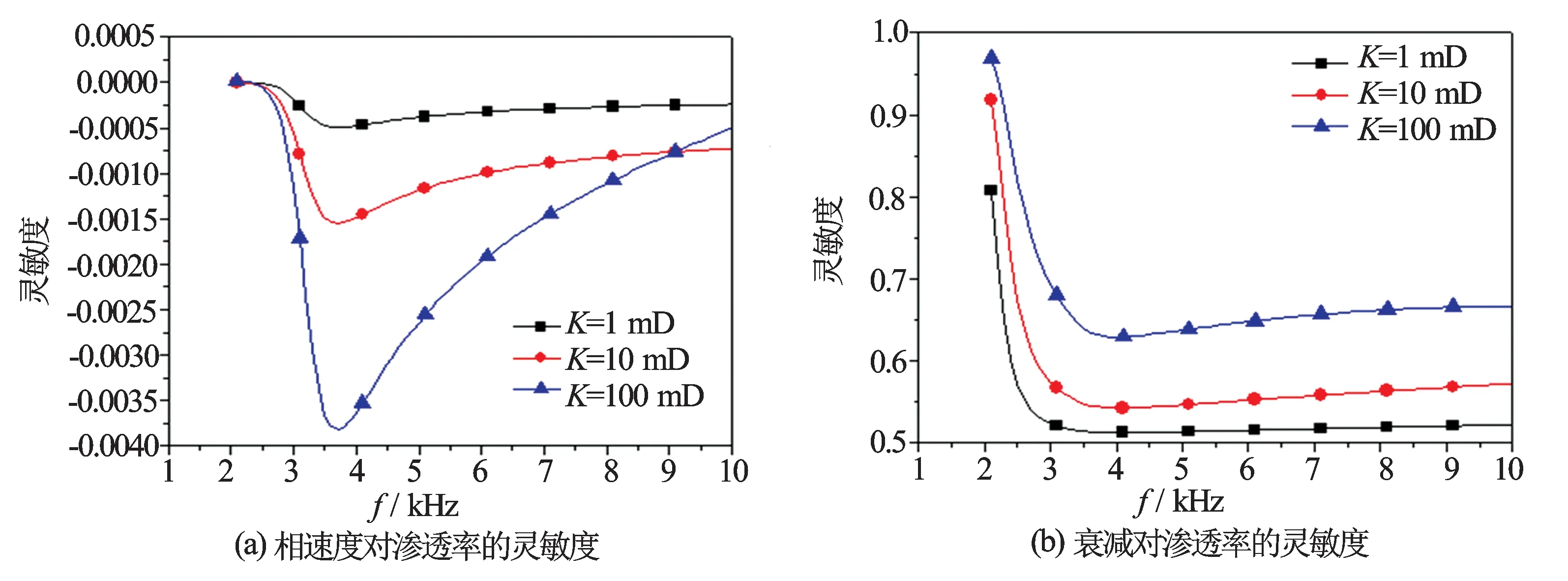
图2 弯曲波的相速度和衰减对不同渗透率基值的灵敏度

图3 弯曲波相速度与衰减对软地层不同参数的灵敏度(渗透率为1 mD)

图4 弯曲波的相速度和衰减对不同渗透率基值的灵敏度

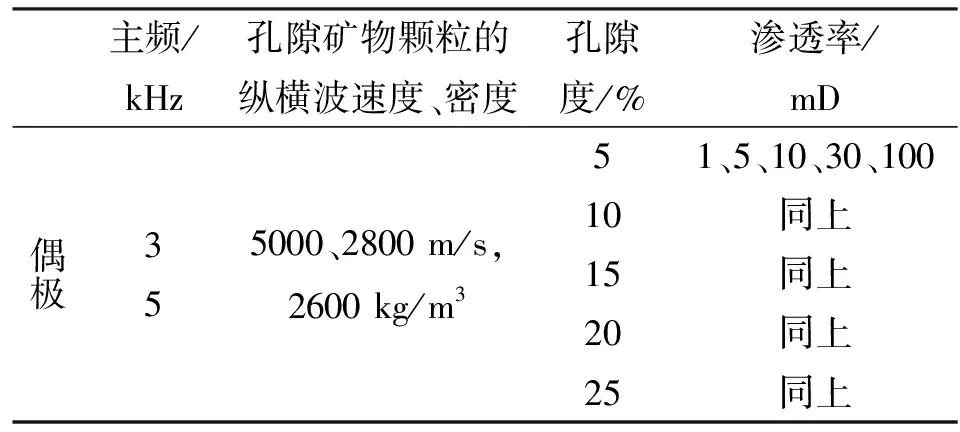
主频/kHz孔隙矿物颗粒的纵横波速度、密度孔隙度/%渗透率/mD偶极355000、2800m/s，2600kg/m351、5、10、30、10010同上15同上20同上25同上

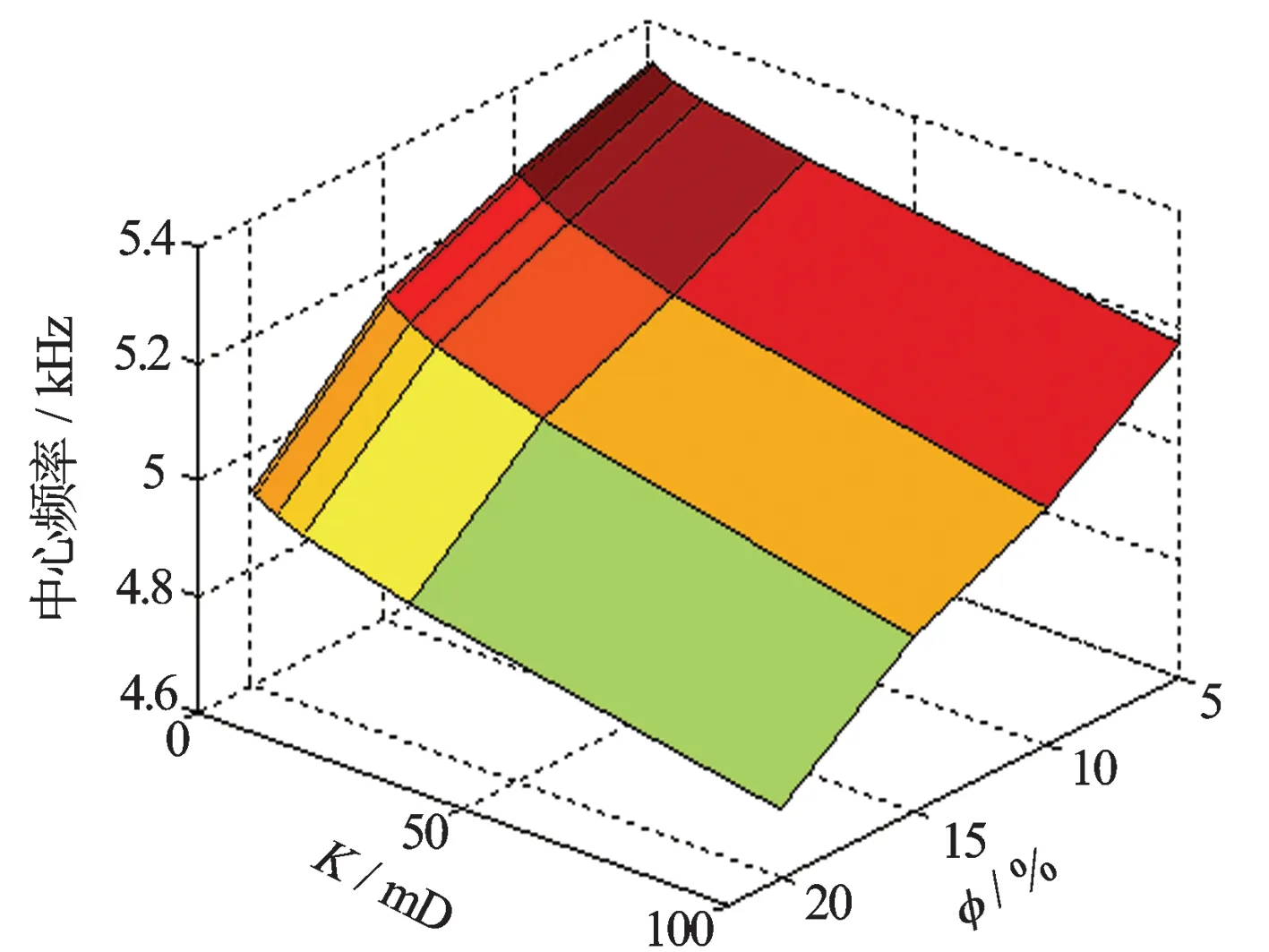
图5 弯曲波中心频率随孔隙度及渗透率变化(声源3 kHz)

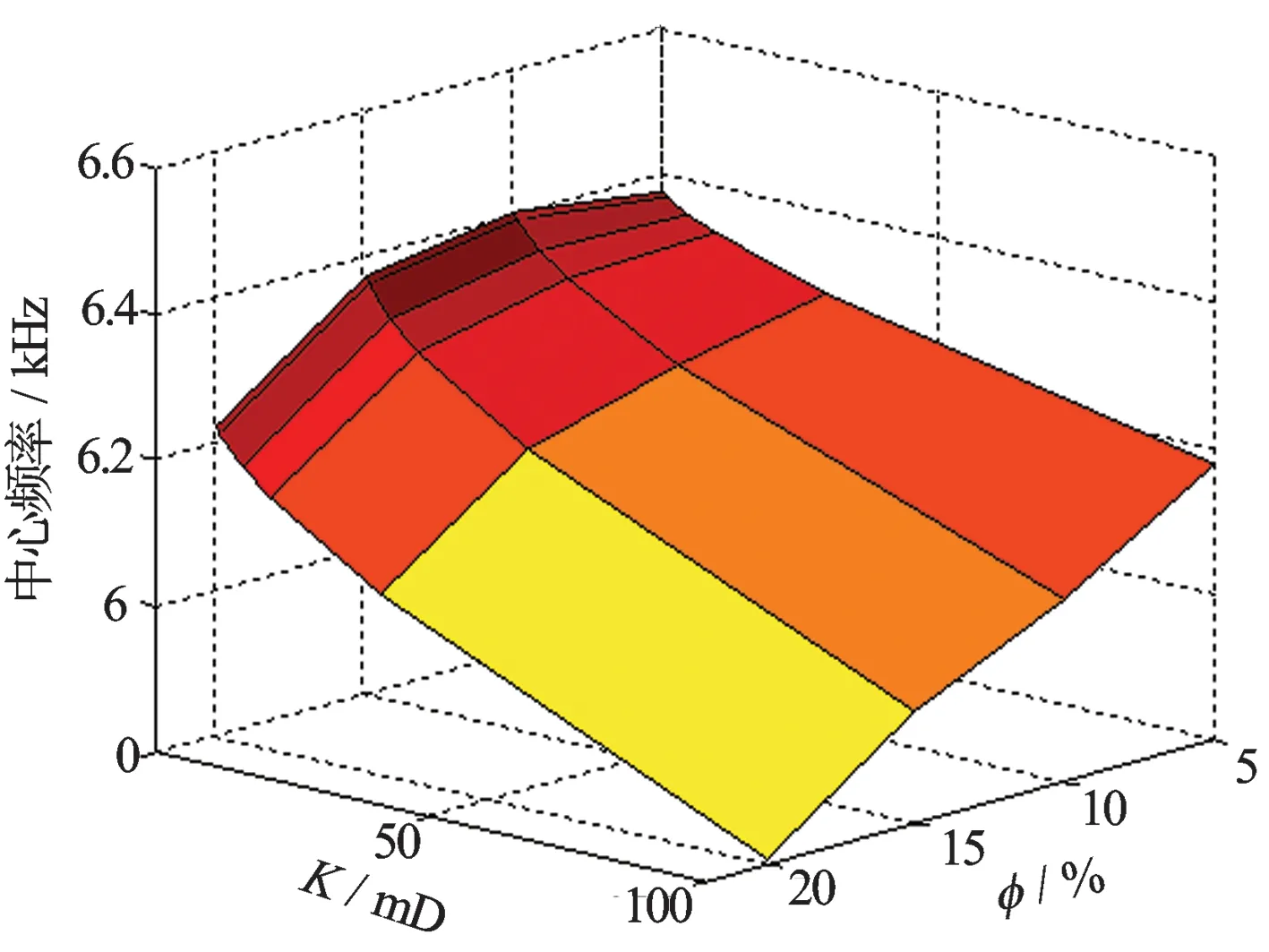
图6 弯曲波中心频率随孔隙度及渗透率变化(声源5 kHz)

2 应用分析

2.1 反演方法

当数值模拟弯曲波的传播时,通常所考虑的主要是地层弹性参数以及井径等与渗透率并无关系的一些参数。而当实际测井时,所测得到的声波不仅包括地层弹性参数与井径等因素的影响,还包括地层渗透率的影响。因此,理论模拟波形与实际所测波形之间的差别主要是由于渗透率的影响造成的。

在弯曲波的理论模拟中,需要给定声源频谱函数,该频谱函数可以利用某完全弹性地层所测弯曲波的波形计算(假定在完全弹性地层渗透率为0)。

实际测量的弯曲波与数值模拟的弯曲波之间的中心频率偏移可以表示为

(8)

选取非渗透层,利用公式(7)求出实测弯曲波波形的中心频率,与数值模拟弯曲波中心频率,构造目标函数,使其差为零,即

Δfc=0

(9)

这就可以运用常用的牛顿迭代法,给定一个初始的声源函数,设置相应的精度,求取声源的频谱函数。

当求得声源频谱函数之后,就可以作为已知参数来模拟弯曲波波形。在渗透性地层中,实测弯曲波波形中心频率与完全弹性地层中模拟弯曲波波形的中心频率会有一定的差异

(10)

在渗透性地层,通过模拟给定渗透率条件下弯曲波波形,并计算其中心频率与完全弹性地层下弯曲波中心频率差异,从而得到频移大小

(11)

(12)

使Δf=0,反演求得地层渗透率真值。

2.2 应用实例

图7是×1井3 520～3 620 m井段砂泥岩地层中利用弯曲波频移计算所得渗透率与岩心渗透率和核磁渗共振透率对比图。从第6道各种渗透率对比中,弯曲波渗透率与核磁共振渗透率、岩心渗透率以及解释渗透率总体上是一致的,在一定程度上能够划分储层。1～3号层,利用频移所得渗透率与其他方法所得渗透率吻合性比较好,在4、5号层位置,核磁共振数据计算结果基本上没有渗透率值,而弯曲波频散反演渗透率结果反映了一定的渗透率,这是因为该段地层有裂隙发育所致(见图8)。