双通道抗模糊测距方法研究
2017-04-25邸成良殷娣娣
邸成良,殷娣娣
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081; 2.国网河北省电力公司信息通信分公司,河北 石家庄 050021)
双通道抗模糊测距方法研究
邸成良1,殷娣娣2
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081; 2.国网河北省电力公司信息通信分公司,河北 石家庄 050021)
航空航天测控系统中,相干测距和非相干测距均存在距离模糊问题,限制了其有效测距范围。针对这一问题提出了在双通道抗模糊测距方案,利用2个通道的测距差值解测距模糊,对测距范围、测距精度和测距周期等指标之间的耦合关系进行了分析。分析结果表明,双通道测距方法有效地解决了测距模糊问题,在很大程度上扩大了测控系统的测距范围。
双通道;距离模糊;相干测距;非相干测距
0 引言
在航空航天测控系统中,通常需要对飞行器进行通信、跟踪测距测角[1],用于实时监控飞行器的运行状态以及空间位置[2]。对于测控系统的测距功能,一般用上下行无线电信号传播时延来确定[3],包含相干测距与非相干测距2种方式[4],相干测距中上下行信号相同或相似[5],非相干测距上下行信号可以相互独立[6]。然而,无论是哪种测距方式,在单一测距体制下,其最大不模糊的测量距离都是有限的,可将这一距离称为整数周期距离。当飞行器与地面站之间距离超过这一距离后,其测距值将产生模糊[7],即无法判断实际间距包含多少个整数周期距离。为了扩大测控系统的测距范围,通常采用多个测距单元协作,确定测距整数周期数量,从而达到解测距模糊的目的。据此,解模糊策略也成为测控系统测距的关键问题之一[8]。
由于测距系统中都存在测距误差,当前对于解算距离模糊一般都是基于优化算法的[9],如余数定理法、模糊函数法[10]和最小二乘法[11]等。其中,余数定理法比较简单,对于理想模型较为实用,但对于参数的轻微误差敏感,容差性能差。模糊函数法则是基于逐点搜索计算、最优点判断的搜索算法,其搜索时间较长。最小二乘法具有运算量小、求解速度快的特点[12],但需要多个测距单元协同工作。基于以上考虑,探索研究一种简单、快速且可靠的解模糊算法就显得尤为重要。为此,开展了双通道抗模糊测距的方法研究。双通道测距中模糊距离的确定通过2个通道测距余量的差值进行判别,然后利用查表法确定最终的测距值。此外,还对查表法进行了拟合优化,大幅减小了查表工作量。双通道测距方法可以同时满足工程应用中测距过程对大范围测量与小计算量的需求。
1 双通道测距原理
相干测距与非相干测距通常以无线信道帧帧头作为测距脉冲,上下行信号的测距脉冲周期与帧频率直接相关[13],而固定的脉冲周期决定了最大无模糊延时为脉冲周期的1/2,进而可以确定最大无模糊测距距离(可称为测距整数周期距离)。当测控站与飞行器之间的距离超过一个整数周期距离后,单一通道测距只能得到一个相对测量值,称为测距余量值。
假设在双通道测距系统中地面站与飞行器之间的间距为X,A通道的最大无模糊测距距离为PA,在测距时间T时刻,A通道测距余量值为ΔxA;相应的,B通道的最大无模糊测距距离为PB,测距余量值为ΔxB,则间距X可表示为:
X=PA·n1+ΔxA,
(1)
X=PB·n2+ΔxB。
(2)
式中,n1和n2为非负整数,对应A通道和B通道测距的整数周期距离数量。
在设计双通道测距系统中,PA和PB的值可以通过配置上下行帧频来改变,假设PA 图1 PA和PB分割间距X示意 在数轴上某个子区间内(如数轴上黑色点位)将对应唯一的一组n1,n2和X值,在整个数轴上所有子区间内,这3个参数与ΔxA-ΔxB的对应关系如表1所示。通过式(1)和式(2)可得: ΔxA-ΔxB=PB·n2-PA·n1。 (3) 对比图1和表1可知,0~(N1·PA),每个子区间内都对应唯一的(n1,n2)值。在该范围内,通过式(3)又可以确定唯一的ΔxA-ΔxB值。因此,在实际测距过程中,通过2步计算间距X:① 分别得到2个通道的测距余量值ΔxA和ΔxB,计算二者的差值,一般测距航空航天测距精度优于几十米量级[14],因此ΔxA-ΔxB的精度也为几十米量级;② 通过查询表1确定n1,n2的值[15],再通过式(1)和式(2)确定实际间距X。总之,就是得到ΔxA-ΔxB的值后,即可在0~(N1·PA)确定实际间距X的值。 表1 测距过程多参数关系 由以上分析可以得出:双通道测距范围比A通道扩大了N1倍,比B通道扩大了N2倍,通过合理配置参数PA和PB可以使双通道测距过程无模糊距离大幅度扩大。而且,在后续仿真过程中,还将对查表法进行优化,缩小查表法的计算量。 此外,在计算间距X过程中,最关键的步骤就是确定n1和n2的数值,除这2个参数外,还需要注意的是PA和PB的最大公约数(GreatestCommonDivisor,GCD)。将表1中的ΔxA-ΔxB的值按照从小到大的顺序排列后可以形成等差数列[16],这个等差数列的增量等于PA与PB的最大公约数。如果最大公约数的值比ΔxA-ΔxB的检测精度还要低,那查表后将无法确定n1和n2的值,换言之,PA和PB的最大公约数要远大于单通道的测距精度,一个合理的取值应该是ΔxA或ΔxB的检测精度的10倍,即百米量级。 综合以上分析,可以得出:理想情况下,PA和PB的最小公倍数决定了最大无模糊测距范围,而PA和PB的最大公约数则关乎能否成功通过ΔxA-ΔxB的值查表得到n1和n2的值。在实际应用中,LCM和GCD的值最终决定于上下行无线信号的帧频,LCM和GCD之间呈反比,不可能同时增大。因此应根据实际情况合理设计信号帧频。 设计双通道抗模糊测距方法的首要问题是确定A通道和B通道的无模糊距离PA和PB。假设PA和PB分别为2 800km和3 000km。二者的最小公倍数为42 000km,最大公约数为200km(为了作图效果,最大公约数远远大于测距精度)。ΔxA和ΔxB的值等于实际间距X对PA和PB求余数。在整个数轴上,ΔxA和ΔxB的数值变化情况如图2所示。 图2 ΔxA和ΔxB在数轴上分布示意 图3 ΔxA-ΔxB在数轴上分布示意 (4) 确定n1,n2值后,将2个通道的测距余量值ΔxA和ΔxB代入式(1)和式(2),可以得到A通道和B通道的无模糊距离XA和XB。最终系统的测距值取二者的均值, X=1/2·XA+1/2·XB。 (5) 由误差理论可知,若XA和XB为独立同分布,则式(5)中X的期望与XA和XB相同,而方差可以减小一半,一定程度上提升了系统精度。 仿真分析表明,通过合理地设置单通道的测距无模糊测距PA和PB的值,可以有效扩大测量范围。本文所用数值为PA=2 800km,PB=3 000km,最大测量范围可以提升至42 000km,满足卫星的测距要求。在深空通信测距中距离探测需求会大大提升,这种情况下只需要将PA和PB设计的更加接近,则可以大大提升测距范围[17]。如取PA=2 990km,PB=3 000km,则二者最小公倍数即测距距离可以达到897 000km,超过了地月之间的探测距离。 单通道测距中,最大无模糊距离小,限制了其测距范围。本文所述的双通道抗模糊测距的方法可以有效扩大航空航天系统中的测距范围。理论推导表明,扩大测量范围的双通道测距方法中有A通道和B通道的测距余量PA和PB这2个重要参数。二者的LCM决定了间距X的测量范围,二者的GCD共同决定了测距系统的精度容差。测距范围和精度容差不能同时提高,应根据实际需求对PA和PB参数进行配置。此外,仿真分析还表明,所述的双通道测距解模糊方法具有解算简单、计算量小的优点,这将有利于测距系统的工程实现。 [1] 于志坚.我国航天测控系统的现状与发展[J].中国工程科学,2006,8(10):42-46. [2]WARNICKKF,MAASKANTR,IVASHINAMV,etal.High-sensitivityPhasedArrayReceiversforRadioAstronomy[C]∥ProceedingsoftheIEEE,2016,104(3):607-622. [3] 楼德侃,李志强,南海涛.DS/FH信号的测速测距性能分析[J].无线电通信技术,2013,39(3):64-66. [4]OLSENKE,CHRISTIANSENJM.RangeandDopplerWalkinDVB-TBasedPassiveBistaticRadar[C]∥Proc.ofIEEERadarConference,2010,29(16):620-626. [5] 吴 军,洪光烈,何志平,等.一种大测距动态范围高重频相干测距测速激光雷达(I):体制及性能[J].红外与毫米波学报,2014,33(6):680-690. [6] 周 侃,张 娜,高红涛.非相干测距技术在无人机测控中的应用[J].无线电工程,2006,36(8):28-29. [7]KRICHELNJ,MCCARTHYA,BULLERGS.ResolvingRangeAmbiguityinaPhotonCountingDepthImagerOperatingatKilometerDistances[J].Opticsexpress,2010,18(9):9 192-9 206. [8] 乐 意,许贤泽,李忠兵,等.基于超定方程组的相位激光测距解模糊算法[J].仪器仪表学报,2012,33(4):930-935. [9] 彭王奇,马 宏,王元钦.双频伪码测距快速求解模糊度方法的仿真研究[J].装备指挥技术学院学报,2006,17(4):87-91. [10] 薛 飞,孙洪忠.雷达导引头解距离模糊算法分析与仿真[J].现代电子技术,2010,21(4):57-60. [11] 邹见效,王厚军,舒 军,等.一种基于最小二乘法的FPN与规则权值优化新方法[J].电子测量与仪器学报,2010,24(7):667-672. [12] 魏绍亮,陈一民.基于最小二乘法的超声波传感器拟合与测距实现研究[J].信号与系统,2004,7(4):30-33. [13] 于起峰,李 强,雷志辉,等.基于序列图像的无人机自测速方法与试验[J].航空学报,2009,30(8):1 503-1 507. [14] 王世练,路 军,张尔扬.基于星间无线电测距的卫星自主定轨与导航[J].宇航学报,2002,23(1):69-72. [15] 周 闰,高梅国,韩月秋.余差查表法解多目标距离模糊算法[J].北京理工大学学报,2002,22(2):221-223. [16]DIC,YANW,HUS,etal.Moiré-basedAbsoluteInterferometrywithLargeMeasurementRangeinWafer-maskAlignment[J].IEEEPhotonicsTechnologyLetters,2015,27(4):435-438. [17] 李 勇,师民祥.12m深空组阵天线设计与工程实现[J].无线电通信技术,2015,41(5):60-63. 邸成良 男,(1988—),博士,工程师。主要研究方向:无人机测控。 殷娣娣 女,(1987—),硕士,助理工程师。主要研究方向:智能电网通信。 Research on Dual-channel Anti-ambiguity Ranging Method DI Cheng-liang1,YIN Di-di2 (1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China; 2.StateGridHebeiInformationandTelecommunicationBranch,ShijiazhuangHebei050021,China) In aerospace TT&C system,both coherent and incoherent ranging methods undergo the range ambiguity problem,which limits their effective ranging scope.To solve this ambiguity problem,a dual-channel anti-ambiguity method is proposed.In this method,the difference value between two channels is used to solve the ranging ambiguity.Further on,the coupling relationships within ranging scope,ranging resolution and ranging period are analyzed in detail.Analysis results show that the ambiguity problem could be solved by dual-channel ranging method,and at the same time,the ranging scope would be expanded in a great level. dual-channel;range ambiguity;coherent ranging;incoherent ranging 10.3969/j.issn.1003-3106.2017.05.14 邸成良,殷娣娣.双通道抗模糊测距方法研究[J].无线电工程,2017,47(5):58-61.[DI Chengliang,YIN Didi.Research on Dual-channel Anti-ambiguity Ranging Method[J].Radio Engineering,2017,47(5):58-61.] 2017-02-08 河北省自然科学基金资助项目(F2014210123)。 TN911.7 A 1003-3106(2017)05-0058-04

2 双通道测距仿真分析


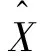

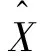
3 结束语
