基于ANSG的雷达信号DOA估计算法
2017-04-25曾小东
曾小东
(中国西南电子技术研究所,四川 成都 610036)
基于ANSG的雷达信号DOA估计算法
曾小东
(中国西南电子技术研究所,四川 成都 610036)
针对阵列信号处理中雷达信号的波达方向(DOA)估计,提出自适应噪声子空间生成(ANSG)算法。通过数值方法,得到阵列接收信号的协方差矩阵,以迭代方式处理约束最小化问题,实现ANSG。根据噪声子空间的表达式获得DOA估计,并且先验信息可以很好地融入算法的流程中,能够有效地解决复杂环境下的多信号源DOA估计问题。仿真结果表明,该算法适用于单频、线性频率调制以及二进制相移键控雷达信号,DOA估计精度和运算速度优于MUSIC。
噪声子空间;超分辨;波达方向估计
0 引言
波达方向(Direction of Arrival,DOA)估计是现代信号处理的重要研究内容之一[1]。针对不同的信号环境,提出了一系列的解决方法[2]。文献[3-4]研究了DOA估计中的相干处理方法。文献[5]针对强信号背景下弱信号DOA估计问题,提出了一种基于噪声子空间扩展的弱信号DOA估计算法。文献[6]在所有信号的幅度均值相等且不为零的前提下,推导出噪声子空间的解析形式,实现了信号DOA的快速估计。文献[7-8]针对非等功率信号DOA估计问题,提出一种基于噪声子空间特征值重构(Eigenvalue Reconstruction of Noise Subspace,ERNS)的超分辨算法。本文在前人研究的基础上,考虑雷达信号侦察的非协作应用环境,对于典型的单频信号、线性频率调制(LFM)信号以及二进制相移键控(BPSK)信号,研究了一种基于自适应噪声子空间生成(ANSG)的DOA估计算法,利用噪声子空间的表达式,迭代实现多信号DOA估计。由于本方法的计算方式为迭代运算,不需要矩阵分解等复杂过程,因此计算效率高于传统算法。
1 信号模型
阵列接收信号为:
x(n)=r(n)+g(n)=As(n)+g(n)。
(1)
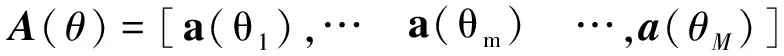
定义阵列接收信号x(n)的协方差矩阵为:
R=E[x(n)xH(n)]=
E[A(θ)s(n)sH(n)AH(θ)]+
E[r(n)gH(n)]+E[g(n)rH(n)]+
E[g(n)gH(n)] 。
(2)
假设接收信号r(n)和噪声g(n)不相关,
E[r(n)gH(n)]=0,E[g(n)rH(n)]=0,
R=A(θ)E[s(n)sH(n)]AH(θ)+E[g(n)gH(n)]=A(θ)RsAH(θ)+Rg。
(3)

2 自适应噪声子空间生成
自适应滤波的典型流程如图1所示。

图1 自适应滤波
将阵列接收信号x(n)通过图1的空域滤波器wL∈CL×1,得到

(4)
定义估计误差为:
e(n)=d(n)-y(n)。
(5)
式中,d(n)为期望信号,对于ANSG而言,d(n)=g(n)。
为寻找使估计误差e(n)在最小二乘意义下取得极小值的wL,首先定义代价函数C为估计误差的平均功率,即
(6)
式中,q=E{x(n)g(n)H}。
式(6)求梯度得
。
(7)
RwL0=q=0。
(8)
因为信号和噪声不相关,故q=0。所得到的滤波器系数wL0生成噪声子空间,为相位差φ1,φ2…φM的表达式。在自适应处理中,假设φ1,φ2…φM-1已知,代价函数C(wL(φM))取得极小值,有
RwL(φM)=0。
(9)
式中,



(10)
代入式(10)得[9]:

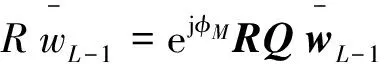

(11)

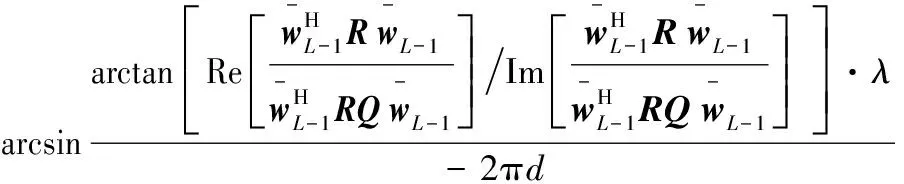
(12)
式中,d为基线长度;λ为信号波长。
3 DOA估计

自适应噪声子空间生成下的DOA估计算法,主要流程为:
步骤1:估计信号源个数M[10]。
步骤2:划分子阵并计算协方差矩阵。将均匀线阵划分为若干子阵,每个子阵的阵元数为M+1,设划分步进为K,K≥1,则子阵数为:

(13)
式中,⎣·」代表向下取整。协方差矩阵R取H个子阵的协方差矩阵平均值。
设定迭代次数初值μ=1,收敛条件0<χ<1[11]。
按照
(14)

步骤5:迭代更新代价函数。
当[(C0-C1)/C0]>χ且μ≤M时,μ=μ+1,C0=C1返回步骤4,否则进入步骤6。
(15)
4 仿真分析
为了验证本文算法的有效性,做了如下仿真。仿真中采样频率为100 MHz,脉冲宽度2 μs。2个信号的波达方向为π/3和π/5。2个单频信号的载频为10MHz和30MHz。2个LFM信号的起始频率为10MHz和30MHz,带宽10MHz。2个BPSK信号的载频为10MHz和30MHz,码速率2MHz。信噪比(SNR)取值范围-5~30dB。每种情况下的MonteCarlo仿真次数为1 000次。波达方向估计的归一化均方根误差(NRMSE)如下所示。
仿真条件1:阵元间隔λ/4,阵元数L=M+1,迭代初始值[0 0],迭代次数N=M+1,不同信号类型的DOA估计如图2所示。

图2 不同信号类型DOA估计的NRMSE
图2中,min表示π/5估计,max表示π/3估计(图3和图4中min和max的含义与图2相同)。由图2可知,本文算法适应于多种窄带和宽带雷达信号的波达方向估计,BPSK信号估计性能和单频信号相当,LFM信号估计性能优于BPSK信号和单频信号。
仿真条件2:阵元间隔λ/4,阵元数L=M+1,迭代初始值[0 0],迭代次数N=M以及阵元间隔λ/4,阵元数L=M+1,迭代初始值[π/2 π/2],迭代次数N=M,单频信号的DOA估计如图3所示。

图3 不同初始值DOA估计的NRMSE
对比图3(a)和图3(b)可知,初始值的选取对估计精度有影响,在无先验知识的前提下,一般选初始值为[0 0]。迭代次数越多,空域滤波的估计误差越小,DOA估计精度越高。
仿真条件3:阵元间隔λ/4,阵元数L=M+2,迭代初始值[0 0],迭代次数N=M+1,不同信号类型的DOA估计如图4所示。
由图4可知,随着阵元数的增加,DOA估计的精度提高,但子阵求协方差矩阵均值的方式对DOA估计精度的改善有限。
仿真条件4:阵元间隔λ/4,阵元数L=M+1,波达方向π/3,信噪比5dB,仿真次数1 000次。不同方法对单频信号DOA估计精度以及运行时间如表1所示。
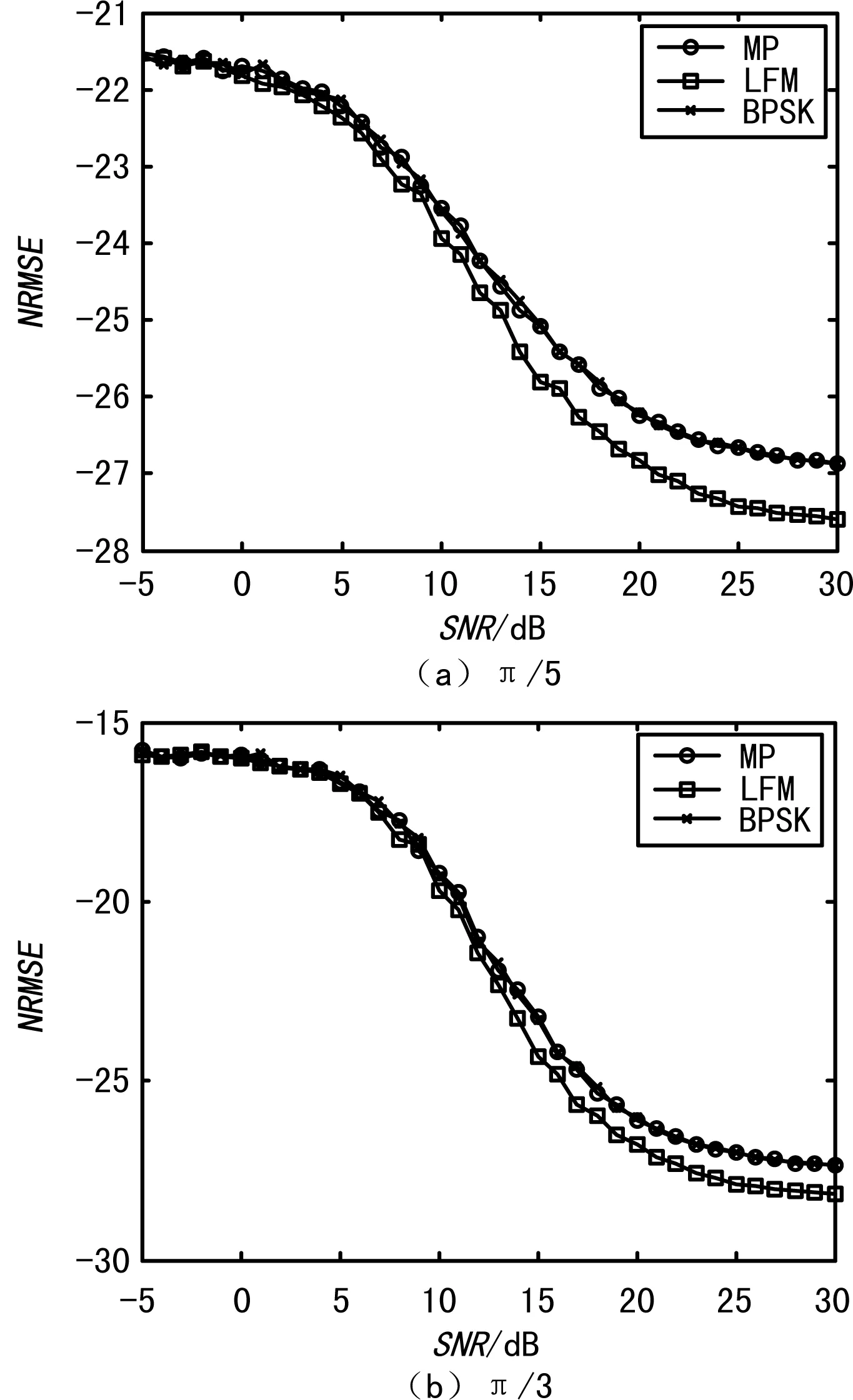
图4 不同阵元数DOA估计的NRMSE

DOA估计算法NRMSE运行时间/ms干涉仪-5.76188MUSIC-13.01925本文算法-16.59673
对比3种算法,干涉仪[12]的运算速度最快,但精度最差。本文算法估计精度与MUSIC[13]算法相当,同时运算速度降低,是一种易于工程实现的DOA估计算法。
5 结束语
针对典型的单频、LFM和BPSK雷达信号,基于自适应噪声子空间生成,研究了一种快速、高精度的DOA估计算法。本文利用空间自适应滤波,研究了阵列信号处理中的噪声子空间生成,并在此基础上,对于均匀线阵的接收信号,进行迭代滤波处理,不依赖被测信号的先验知识,在阵元数大于信号个数时,可以估计同时到达多信号的来波方向,尤其是本方法中运用的迭代方式,避免了矩阵求逆等复杂运算,因而计算量小,实时性高,具有一定的工程应用前景。
[1] WANG G,XIN J,WANG J,et al.Subspace-based Two-dimensional Direction Estimation and Tracking of Multiple Targets[J].IEEE Transactions on Aerospace and Electronic Systems,2015,51(2):1 386-1 402.
[2] 杨荣山,张 宁,张 玉.基于L型阵的ESPRIT算法在DOA估计中的应用[J].无线电通信技术,2013,39(4):85-88.
[3] 刁 鸣,安春莲.独立信号和相干信号DOA估计新方法[J].系统工程与电子技术,2011,33(12):2 582-2 586
[4] 邓超升,朱立东.基于奇异值分解和相干积累的DOA估计方法[J].无线电通信技术,2016,42(2):27-31.
[5] 张 静,廖桂生,张 洁.强信号背景下基于噪声子空间扩充的弱信号DOA估计方法[J].系统工程与电子技术,2009,31(6):1 279-1 283.
[6] 艾名舜,马红光,刘 刚.基于噪声子空间解析形式的快速DOA估计算法[J].电子与信息学报,2010,32(5):1 071-1 076.
[7] FANG Q Y,CAO B X,JIN M,et al.Reconstruction of Eigenvalues in Noise Subspace for Unequal Power Sources DOA Estimation[C]∥IEEE Radar Conference,Cincinnati,OH,USA,2014:591-596.
[8] 方庆园,韩 勇,金 铭,等.基于噪声子空间特征值重构的DOA估计算法[J].电子与信息学报,2014,36(12):2 876-2 881.
[9] ENRIQUE A S,MOHAMMAD S.Noise Subspace-Based Iterative Technique for Direction Finding[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(4):2 281-2 295.
[10] 何子述,夏 威.现代数字信号处理及其应用[M].北京:清华大学出版社,2009.
[11] JIN H C,CHANG D Y.Underdetermined High-Resolution DOA Estimation:A2ρth-OrderSource-Signal/NoiseSubspaceConstrainedOptimization[J].IEEETransactionsonSignalProcessing,2015,63(7):1 858-1 873.
[12] 魏合文,王 军,叶尚福.一种基于余弦函数的相位干涉仪阵列DOA估计算法[J].电子与信息学报,2007,29(11):2 665-2 668.
[13] 周小军,谭 薇,冯大政,等.基于解相干的改进MUSIC算法DOA估计[J].无线电工程,2014,44(12):18-21.
曾小东 男,(1985—),工程师。主要研究方向:信号处理和航空电子学。
Radar Signal DOA Estimation Algorithm Based on Adaptive Noise Subspace Generation
ZENG Xiao-dong
(SouthwestChinaInstituteofElectronicTechnology,ChengduSichuan610036,China)
This paper proposes an Adaptive Noise Subspace Generation (ANSG) algorithm for the Direction of Arrival (DOA) estimation of radar signal in the area of array signal processing.The covariance matrix of the received signal is obtained by numerical methods.Then,the constrained minimization problem is solved iteratively for the ANSG.With the expression of the noise subspace,the DOA estimation is gained.Furthermore,the algorithm can readily incorporate prior knowledge into the DOA estimation process and efficiently estimate DOAs of multiple sources under complex environment.The simulation results show that it is applicable for monopulse,LFM and BPSK radar signals.This algorithm is better than MUSIC in terms of the accuracy and speed of DOA estimation.
noise subspace;super resolution;direction-of-arrival estimation
10.3969/j.issn.1003-3106.2017.05.08
曾小东.基于ANSG的雷达信号DOA估计算法[J].无线电工程,2017,47(5):32-36.[ZENG Xiaodong.Radar Signal DOA Estimation Algorithm Based on Adaptive Noise Subspace Generation[J].Radio Engineering,2017,47(5):32-36.]
2017-01-23
国家部委基金资助项目。
TN 911.7
A
1003-3106(2017)05-0032-05
