基于小波变换的调制识别算法

王东旭+陈殿仁+李兴广+陈磊

摘要：小波变换作为一种特征提取工具[1]，它能够在时域和频域这两个域中体现信号的部分特征。ASK、PSK和FSK通信信号的连续符号之间，由于幅度参数、相位参数或者频率参数变化，会导致突然急剧的变化[2]。本文利用小波变换，探究以上通信调制信号在小波变换下时域和频域特性。最后仿真说明算法性能。

关键词：小波变换；特征提取；时频域

中图分类号：TN911.23 文献标识码：A 文章编号：1007-9416（2017）01-0120-01

目前，小波变换的体系已经很完备，受到了广泛的关注，它作为应用数学的重要组成部分，在工程中的应用越来越广。根据小波变换理论，它用小波的基函数来构成信号。小波用尺度和位移来表征，而基函数就是用母小波通过伸缩和平移得到的。这样看来，所有信号都能够用小波的尺度及位移来体现其特点。通过小波变换可以同时观察信号的时间分辨率和频率分辨率，在这方面，傅里叶变换是不能实现的。小波变换的应用范围很广，例如信号处理和建模，信号编码，多分辨力分析[3]，视频压缩等[4]，它尤其适合对突变情况下信号的分析和處理。近些年来，将其用在制式识别方面也是一个重点方向。

小波在制式识别中主要用来从信号中提取能够表征信号制式特点的特征量，获得它们的轮廓和细节等信息，之后根据这些信息选取适当的分类准则，实现对信号制式的分类识别[5]。不同的数字调制信号，当一个码元从前一个码元持续时间过渡到另一个码元持续时间的时候，调制信号的幅度、相位或者频率可能会发生变化。而制式分类特征就在上面的变化中。所以应用小波变换检测以上突变，能够达到制式分类的目的。

用小波变换进行制式分类的特征明显，它的实现有很多快速算法，而且处理速度快，能够保证工程应用的实时性，由于以上优点，本文应用它作为制式识别的方法，关于它的理论及相关制式分类方法，下面将会详尽地说明。

1 信号模型的建立

接收的中频信号是，它的复数形式是：

（1）

式中是已调制复信号，是高斯白噪声的复数形式，其功率，为信号经过下变频处理后的中频角频率，是相应的中频频率，是载波的初始相位。

对PSK信号来说，

（2）

对于FSK信号，

（3）

对于ASK信号，

（4）

在（2）式、（3）式和（4）式中，是信号功率，是观测符号数目，是FSK第个符号相应的角频率，是符号周期，是单位矩形函数，范围。

2 调制分类和仿真

上面提到了信号的小波变换幅值通过中值滤波能够将幅值的尖锐部分去除掉，下面通过仿真对其进行说明。

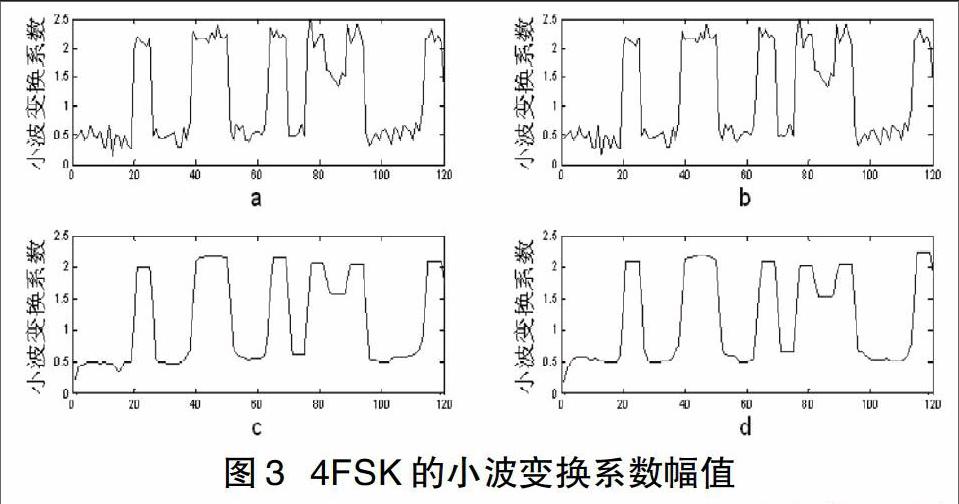
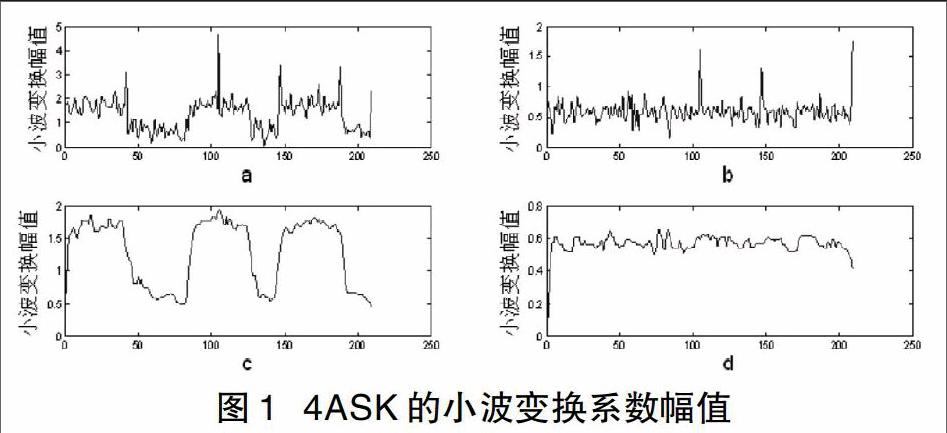
图1是对4ASK信号进行小波变换后，信号的小波变换系数幅值，图1中a是幅值未归一化的4ASK信号的小波变换幅值。a中的小波变换幅值经过中值滤波处理，得到c。b是经过幅值归一化处理的4ASK信号的小波变换幅值，b中的数据经过中值滤波，得到d。图2是对4PSK信号进行小波变换后，信号的小波变换系数幅值，图2中a是幅值未归一化的4PSK信号的小波变换幅值。a中的小波变换幅值经过中值滤波处理，得到c。b是经过幅值归一化处理的4PSK信号的小波变换幅值，b中的数据经过中值滤波，得到d。图3是对4FSK信号进行小波变换后，信号的小波变换系数幅值，图3中a是幅值未归一化的4FSK信号的小波变换幅值。a中的小波变换幅值经过中值滤波处理，得到c。b是经过幅值归一化处理的4FSK信号的小波变换幅值，b中的数据经过中值滤波，得到d。

3 结语

本文采用小波变换的算法机理对信号制式识别进行了研究。假定噪声为加性高斯白噪声，选取了最优的尺度因子和适当的阈值，使用MATLAB进行了仿真实验，说明了信号在小波变换下的特征参量的有效性，验证了算法的性能。

参考文献

[1]周敏.数字通信信号制式自动识别与参数估计算法研究与实现[D].西南交通大学，2013.

[2]汤卫东.基于小波变换的数字通信信号调制识别研究[D].西安电子科技大学，2010.

[3]孙晓丽.基于小波矩特征的小波神经网络目标识别研究[D].东南大学，2006.

[4]矫媛.小波变换在图像降噪中的应用研究[D].青岛大学，2008.

[5]王晓侠，窦红真，王芳. 基于小波分析的调制识别技术研究[J].数字技术与应用，2013（10）：113-115.