电力图形系统应用中SVG文件压缩算法
2017-04-25卢军雄钟俊
卢军雄+钟俊


摘要:针对可缩放矢量图形(SVG)作为矢量图形格式优势明显,但存储时占用内存较大和SVG文件数据大量冗余的特点,提出分别使用Huffman算法和LZSS算法对电力系统图形数据载体SVG文件进行压缩,在满足压缩时间的前提下,LZSS算法相对于Huffman算法压缩率更高。LZSS算法性能能满足电力系统应用SVG文件压缩要求。
关键词:电力图形系统;SVG文件;Huffman;LZSS
中图分类号:TN919.8 文献标识码:A 文章编号:1007-9416(2017)01-0115-04
随着电力系统规模的扩大和系统结构越发复杂,利用计算机技术开发出界面友好图形化软件对于提高电力系统自动化具有重要的意义。SVG作为W3C推出的一种基于XML文本性矢量描述语言,被IEC61970推荐为图形文件的基本格式,逐步成为行业标准[1]。SVG文件的优点为。
(1)表达能力强,删除和添加方便;
(2)支持图形无失真缩放;
(3)支持动画和互动。
SVG文件是纯粹的XML,拥有XML的所有特性,SVG作为电力图形系统数据载体已逐步成为一种趋势[2]。SVG文件以树的形式管理SVG元素,SVG元素都是基本图元与其属性构成的文本,基本图元有直线、圆、椭圆、文本、圆弧等,每一种图元都有相应的属性,如颜色、线宽、填充等。例如一个圆的SVG元素定义为
信息论之父Claude Shannon认为信息都存在冗余,SVG文件存在很多相同的属性文本,信息冗余量很大,有必要对SVG文件进行压缩。本文分别从统计编码Huffman编码和字典编码LZSS两种编码方案对SVG文件进行压缩,实验表明LZSS压缩算法的压缩比更高。
1 Huffman编码和LZSS编码原理
1.1 Huffman编码
Huffman编码是一种基于统计的变长编码,在编码前统计各模式的频率,根据不同模式的频率采用不同长度码字对其编码(对于出现频率高的模式,其编码的长度最短)。Huffman采用前缀码的方法表示每一个字符,前缀码有时也称前缀树[3],其特点是任何一个字符的编码都不能作为另外一个字符编码的前缀,这样可以大大简化解码过程,解码器只需要识别一个完整的前缀码就能解码当前字符,而不需要进一步读取后面的编码。Huffman编码的平均长度,在类似的编码方案中,Huffman编码获得的编码效果最好[4]。
Huffman编码过程是通过Huffman树的构建过程完成的。首先将字符的统计结果按照字符出现频率的降序排列,记待编码的数据为个数为n的字符集,集合;字符出现频率为,,集合为Huffman编码的二进制输出,为字符对应的二进制编码。编码带权路径长度,为编码输出的二进制长度。构造一个Huffman树的简单过程如图1。
表1展示了8个字符A∶K出现频率和经过Huffman编码后对应的二进制输出。
编码输出的带权路径长度为=2.58,而采用二进制编码需要的带权路径长度为3。根据表中字符出现的频率选择出现频率最小的两个字符A,B构造树,其左孩子为A,出现频率为0.01,右孩子为B,出现频率0.05,根节点为左右孩子出现频率之和0.06;并将字符A,B从字符集中删除。同时将作为新的字符加入字符集中,此时频率最小的两个节点是和字符F,同样按照构造树方式构造出整个Huffman树如图1。
1.2 LZSS编码原理
LZSS编码原理不同于基于统计方式的Huffman编码,它是基于字典压缩算法LZ77算法的改进,不再需要统计字符出现频率[5]。LZ77使用已出现的字符串的相关信息来表示当前需要被编码的字符串,在此过程中使用滑动窗口完成字符流的输入和字符串的匹配。在编码过程中,字符缓冲区的大小设定为N,已压缩好字符串的长度为M(M 压缩开始前,缓冲区设为空,字符串以字符流的方式从右至左进入超前查看缓冲区,找出超前查看缓冲区和正文窗口的匹配的最长字符串,假设找到最长匹配字符串,其起始位置为s,长度为L(长度可以为0),出现第一个不匹配的字符位置为e,这样从当前编码位置开始到第一个不匹配的字符可以编码为,且满足。如果编码信息占用空间比个字节小,便实现了字符串的压缩。具体算法流程如图3。 LZ77压缩算法存在时间和空间的性能约束: 在压缩时间上存在性能瓶颈:超前查看缓冲区字符与正文字典匹配采用的是线性的匹配方式,超前查看窗口的大小为,正文窗口大小为M,表2给出了常用字符串匹配算法的平均时间复杂度[7]。 表2给出的算法时间复杂度最好的情况还是线性的,LZ77算法正文窗口一般设置为几千,超前查看缓冲区设置位十几,在进行字符串匹配时严重影响算法的时间性能[8]。而且都是相关窗口大小成正比。算法在压缩空间也存在缺陷:当未找到匹配字符串时,输出三元组占用的空间比需要进行编码的字符串占用的空间更大,出现负压缩的情况。 LZSS算法针对LZ77算法的这两点缺点作出了改进。LZSS采用二叉查找树技术替换了滑动窗口的线性查找,超前查看缓冲区字符串进入正文窗口时需要按照二叉查找树的特征加入到二叉树中,采用二叉查找树技术字符串的匹配时间极大优化,在压缩时间上极大地提高了压缩性能[5];LZSS在编码输出采用位标志方式區别输出,输出时编码输出与设定最小字符串长度的大小,只有在编码输出字节数较小采用编码输出,反之输出真正的字符。
2 Huffman编码与LZSS算法实现
2.1 Huffman编码的实现
SVG文件字符采用单字节编码,统计每个字符出现次数使用huffman_node *huffmanArray[0xff]数组便可以将SVG文本字符统计完整。Huffman树节点的数据结构为:
typedef struct huffman_node
{
unsigned char value;
unsigned int count;
bool isDealt;
struct huffman_node *left, *right, *parent;
} huffman_node;
Huffman_node中value表示该节点代表的字符,isDealt表示该字符是否已被处理,在查找字符出现频率最小的两个中经常使用此标记。根据huffmanArray统计结果查找出现频率最小的两个字符,分别作为新建二叉树的左右孩子,二叉树父节点统计频率为左右孩子出现频率之和,并将已加入二叉树的字符标记为已处理。二叉树仍然可以按照单个字符处理,直到所有的字符都被加入Huffman树中。在给编码数组编码时首先访问Huffman树最左边的叶子节点,设定其编码为‘0,然后通过parent指针访问右节点设定编码为‘1,再次通过parent回到父节点,避免使用递归方式遍历树结构带来的时间开销。通过已经编码过的编码数组为SVG文件每一个字符编码,直到文件结束。Huffman编码模块划分如图4。
由于SVG文件所使用的字符都是8位编码字符,编码数组的长度为0xff。编码数组的数据结构为
typedef struct code_list
{
byte_t codeLen;
unsigned int *code;
} code_list;
2.2 LZSS编码的实现
根据前述的LZ77算法,改进后的LZSS算法在编码输出和字符串匹配上实现了优化。其算法的如流程图5。
实现算法的相关数据结构:
超前查看缓冲区和正文缓冲区,根据文件内容上下文依赖关系正文缓冲区大小不尽相同,定义宏WINDOW_SIZE大小为4K,用12bits来表示,所以需要4bits来表示字符串的长度。超前查看缓冲区一般设置为18bits。定义最长不可编码长度为MAX_UNCODED,当匹配字符串与MAX_UNCODED比較时,可以使用ENCODE与UNCODE来标识输出。最大可编码长度为超前查看缓冲区大小设置为MAX_CODE,由匹配字符串长度和最长不可编码长度决定。
字符串编码使用封装长度和位置的数据结构:
typedef struct encoded_string
{
unsigned int offset;
unsigned int length;
} encoded_string;
offset和length可以分别得到字符串编码信息:位置和长度。
二分查找树是二叉树的一种变形,二分查找树根节点存储的关键字总是大于其左子树的关键字,小于右子树的关键字。在建立二分查找树时要按照二叉树关键字的性质建立,对于N个节点的二分查找树查找关键字时,最好的情况下时间复杂度为,大大加速了查找时间。该算法使用的二叉树结构为:
typedef struct tree_node
{
unsigned int left;
unsigned int right;
unsigned int parent;
} tree_node;
该结构体中的left,right,parent都是指向正文缓冲区字符的索引;使用tree_node tree[WINDOW_SIZE]对应每一个正文缓冲区的字符。
在算法进入主循环前需要对正文缓冲区,超前查看缓冲区和二分查找树初始化,InitializeSearchTree()完成树的初始化工作,二分查找树根节点ROOT_INDEX为依照正文缓冲区建立字符串的最后一个窗口为WINDOW_SIZE - MAX_CODED-1,为方便查找和插入操作空节点NULL_INDEX为ROOT_INDEX+1。初始化树根节点的父节点为ROOT_INDEX;剩余所有节点左右孩子和父节点全部清空。
只有超前查看缓冲区不为空,压缩算法将持续进行,主要是对位于超前查看缓冲区的字符串进行编码,二分查找树的字符串删除和添加;MatchString()算法利用二分查找树返回匹配字符串位置和长度,从根节点开始查找匹配字符,如匹配即利用左右节点关键字关系进行下一个字符匹配,直到搜索到叶子节点。将以编码过的字符串加入二叉查找树由AddString()完成,在向二分查找树添加字符串的同时需要将树中旧的字符串删除DeleteString()。
3 压缩算法性能与实验
衡量压缩算法的性能主要有压缩率和压缩耗时,但是这两个指标之间存在矛盾,只能在合适的应用场景折中选择。定义压缩率=压缩文件大小/源文件大小*100%,压缩率越小表明压缩效果越好;压缩耗时是指压缩完文件所需时间。
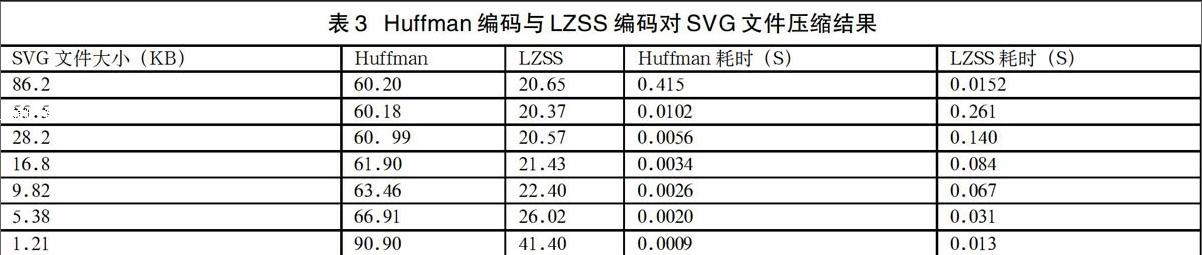
实验设备采用采用Ubuntu 15.10操作系统,CPU型号为Intel(R) Core(TM) i5@2.53GHz,内存大小为4G,Huffman算法和LZSS算法运行环境相同。压缩数据源为电力系统图形界面SVG文件。实验结果如表3。
从表3可以看出对Huffman压缩算法在压缩时间上比LZSS算法好,但LZSS压缩算法在压缩比性能上比Huffman压缩效果好,在存储空间较小的应用场合有一定的应用场景。对于特定的压缩算法,文件在较大时其压缩效果比小文件更好,在电力图形化系统中SVG文件越大,其信息冗余越多,可以压缩的空间越大,压缩率也相对高一些。
参考文献
[1]纪陵,蒋衍君,施广德.基于SVG的电力系统图形互操作研究[J].电力自动化设备,2011,31(7):105-114.
[2]李为,潘秀霞,等.基于SVG标准的电力系统图形编辑器的设计与实现[J].中国电力教育,2008年研究综述与技术论坛专刊.
[3]Utpal Nandi, Jyotsna Kumar Mandal. Windowed Huffman coding with limited distinct symbols[J]. Procedia Technology, 2012, 4:589-594.
[4]Yi Zhang, Zhili Pei, Jinhui Yang, Yanchun Liang. Canonical Huffman code based full-text index[J]. Progress in Natural Science, 2008, 18(3):325-330.
[5]王平著.LZSS文本压缩算法实现与研究[J].计算机工程.2001年8月.第27卷(第 8期).
[6]闾松林.基于字典编解码算法的应用与研究[D].湖南长沙,中南大学,2011:9-11.
[7]王坚.基于后缀数组的滑动窗口匹配压缩改进算法研究[D].湖北武汉,华中科技大学,2012:7-10.
[8]蔡成攀.无损数据压缩技术在嵌入式系统中的应用[D].陕西西安,西安电子科技大学,2007,14-18.
