基于计算机视觉的三维重建技术综述

徐超+李乔

摘要：单目视觉三维重建技术是计算机视觉三维重建技术的重要组成部分，其中从运动恢复结构法的研究工作已开展了多年并取得了不俗的成果。目前已有的计算机视觉三维重建技术种类繁多且发展迅速，本文对几种典型的三维重建技术进行了分析与比较，着重对从运动恢复结构法的应用范围和前景进行了概述并分析其未来的研究方向。

关键词：计算机视觉；三维重建；单目视觉；从运动恢复结构法

中图分类号：TP391 文献标识码：A 文章编号：1007-9416（2017）01-0054-03

计算机视觉三维重建技术是通过对采集的图像或视频进行处理以获得相应场景的三维信息，并对物体进行重建。该技术简单方便、重建速度较快、可以不受物体形状限制而实现全自动或半自动建模。目前计算机视觉三维重建技术广泛应用于包括医学系统、自主导航、航空及遥感测量、工业自动化等在内的多个领域。

本文根据近年来的国内外研究现状对计算机视觉三维重建技术中的常用方法进行了分类，并对其中实际应用较多的几种方法进行了介绍、分析和比较，指出今后面临的主要挑战和未来的发展方向。本文将重点阐述单目视觉三维重建技术中的从运动恢复结构法。

1 基于计算机视觉的三维重建技术

通常三维重建技术首先需要获取外界信息，再通过一系列的处理得到物体的三维信息。数据获取方式可以分为接触式和非接触式两种。接触式方法是利用某些仪器直接测量场景的三维数据。虽然这种方法能够得出比较准确的三维数据，但是它的应用范围有很大程度上的限制。目前的接触式方法主要有CMMs、Robotics Arms等。非接触式方法是在测量时不接触被测量的物体，通过光、声音、磁场等媒介来获取目标数据。这种方法的实际应用范围要比接触式方法广，但是在精度上却没有它高。非接触式方法又可以分为主动和被动两类。

1.1 基于主动视觉的三维重建技术

基于主动视觉的三维重建技术是直接利用光学原理对场景或对象进行光学扫描，然后通过分析扫描得到的数据点云从而实现三维重建。主动视觉法可以获得物体表面大量的细节信息，重建出精确的物体表面模型；不足的是成本高昂，操作不便，同时由于环境的限制不可能对大规模复杂场景进行扫描，其应用领域也有限，而且其后期处理过程也较为复杂。目前比较成熟的主动方法有激光扫描法、结构光法、阴影法等。

1.2 基于被动视觉的三维重建技术

基于被动视觉的三维重建技术就是通过分析图像序列中的各种信息，对物体的建模进行逆向工程，从而得到场景或场景中物体的三维模型。这种方法并不直接控制光源、对光照要求不高、成本低廉、操作简单、易于实现，适用于各种复杂场景的三维重建；不足的是对物体的细节特征重建还不够精确。根据相机数目的不同，被动视觉法又可以分为单目视觉法和立体视觉法。

1.2.1 基于单目视觉的三维重建技术

基于单目视觉的三维重建技术是仅使用一台相机来进行三维重建的方法，这种方法简单方便、灵活可靠、使用范围广，可以在多种条件下进行非接触、自动、在线的测量和检测。该技术主要包括X恢复形状法、从运动恢复结构法和特征统计学习法。

（1）X恢复形状法。若输入的是单视点的单幅或多幅图像，则主要通过图像的二维特征（用X表示）来推导出场景或物体的深度信息，这些二维特征包括明暗度、纹理、焦点、轮廓等，因此这种方法也被统称为X恢复形状法。这种方法设备简单，使用单幅或少数几张图像就可以重建出物体的三维模型；不足的是通常要求的条件比较理想化，与实际应用情况不符，重建效果也一般。

（2）从运动恢复结构法。若输入的是多视点的多幅图像，则通过匹配不同图像中的相同特征点，利用这些匹配约束求取空间三维点的坐标信息，从而实现三维重建，这种方法被称为从运动恢复结构法，即SfM（Structure from Motion）。这种方法可以满足大规模场景三维重建的需求，且在图像资源丰富的情况下重建效果较好；不足的是运算量较大，重建时间较长。

目前，常用的SfM方法主要有因子分解法和多视几何法两种。1）因子分解法。Tomasi和Kanade[1]最早提出了因子分解法。这种方法将相机模型近似为正射投影模型，根据秩约束对二维数据点构成的观测矩阵进行奇异值分解，从而得到目标的结构矩阵和相机相对于目标的运动矩阵。该方法简便灵活，对场景无特殊要求，不依赖具体模型，具有较强的抗噪能力；不足的是恢复精度并不高。2）多视几何法。通常，多视几何法包括以下四个步骤：①特征提取与匹配。特征提取是首先用局部不变特征进行特征点检测，再用描述算子来提取特征点。Moravec[2]提出了用灰度方差来检测特征角点的方法。Harris[3]在Moravec算法的基础上，提出了利用信号的基本特性来提取图像角点的Harris算法。Smith等人[4]提出了最小核值相似區，即SUSAN算法。Lowe[5]提出了一种具有尺度和旋转不变性的局部特征描述算子，即尺度不变特征变换算子，这是目前应用最为广泛的局部特征描述算子。Bay[6]提出了一种更快的加速鲁棒性算子。特征匹配是在两个输入视图之间寻找若干组最相似的特征点来形成匹配。传统的特征匹配方法通常是基于邻域灰度的均方误差和零均值正规化互相关这两种方法。Grauman等人[7]提出了一种基于核方法的快速匹配算法，即金字塔匹配算法。Photo Tourism系统在两两视图间的局部匹配时采用了基于近似最近邻搜索[8]的快速算法。②多视图几何约束关系计算。多视图几何约束关系计算就是通过对极几何将几何约束关系转换为基础矩阵的模型参数估计的过程。Longuet-Higgins[9]最早提出多视图间的几何约束关系可以用本质矩阵在欧氏几何中表示。Luong[10]提出了解决两幅图像之间几何关系的基础矩阵。与此同时，为了避免由光照和遮挡等因素造成的误匹配，学者们在鲁棒性模型参数估计方面做了大量的研究工作，在目前已有的相关方法中，最大似然估计法、最小中值算法、随机抽样一致性算法三种算法使用最为普遍。③优化估计结果。当得到了初始的射影重建结果之后，为了均匀化误差和获得更精确的结果，通常需要对初始结果进行非线性优化。在SfM中对误差应用最精确的非线性优化方法就是光束法平差。光束法平差是在一定假设下认为检测到的图像特征中具有噪音，并对结构和可视参数分别进行最优化的一种方法。近年来，众多的光束法平差算法被提出，这些算法主要是解决光束法平差有效性和计算速度两个方面的问题。Ni[11]针对大规模场景重建，运用图像分割来优化光束法平差算法。Engels[12]针对不确定的噪声模型，提出局部光束法平差算法。Lourakis[13]提出了可以应用于超大规模三维重建的稀疏光束法平差算法。④得到场景的稠密描述。经过上述步骤后会生成一个稀疏的三维结构模型，但这种稀疏的三维结构模型不具有可视化效果，因此要对其进行表面稠密估计，恢复稠密的三维点云结构模型。近年来，学者们提出了各种稠密匹配的算法。Lhuillier等人[14]提出了能保持高计算效率的准稠密方法。Furukawa[15]提出的基于面片的多视图立体视觉算法是目前提出的准稠密匹配算法里效果最好的算法。

綜上所述，SfM方法对图像的要求非常低，鲁棒性和实用价值非常高，可以对自然地形及城市景观等大规模场景进行三维重建；不足的是运算量比较大，对特征点较少的弱纹理场景的重建效果比较一般。

（3）特征统计学习法。特征统计学习法是通过学习的方法对数据库中的每个目标进行特征提取，然后对目标的特征建立概率函数，最后将目标与数据库中相似目标的相似程度表示为概率的大小，再结合纹理映射或插值的方法进行三维重建。该方法的优势在于只要数据库足够完备，任何和数据库目标一致的对象都能进行三维重建，而且重建质量和效率都很高；不足的是和数据库目标不一致的重建对象就很难得到理想的重建结果。

1.2.2 基于立体视觉的三维重建技术

立体视觉三维重建是采用两台相机模拟人类双眼处理景物的方式，从两个视点观察同一场景，获得不同视角下的一对图像，然后通过左右图像间的匹配点恢复出场景中目标物体的三维信息。立体视觉方法不需要人为设置相关辐射源，可以进行非接触、自动、在线的检测，简单方便，可靠灵活，适应性强，使用范围广；不足的是运算量偏大，而且在基线距离较大的情况下重建效果明显降低。

2 分析与比较

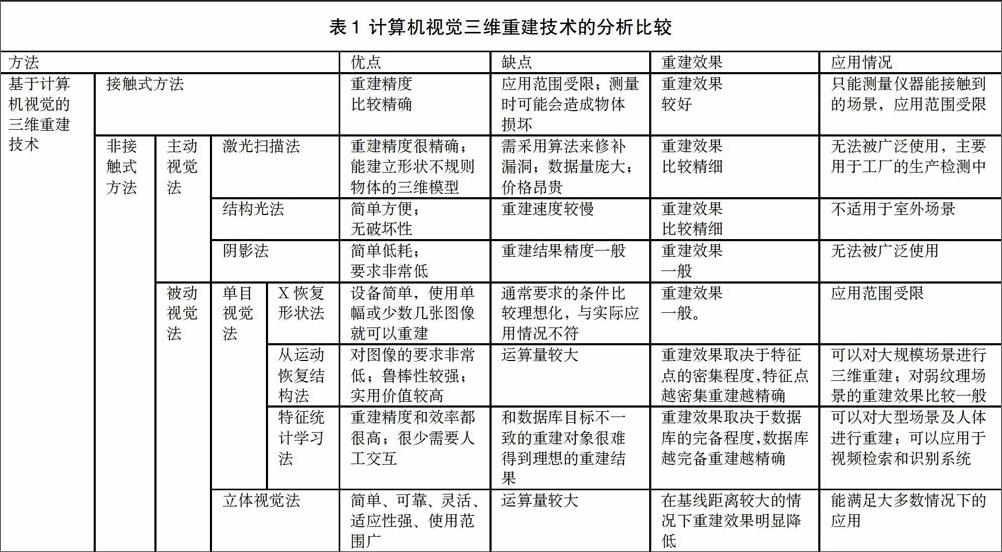
随着上述各个研究方向所取得的积极进展，研究人员开始关注自动化、稳定、高效的三维重建技术的研究。表1是各种计算机视觉三维重建技术的分析与比较。

3 面临的问题和挑战

SfM方法目前存在的主要问题和挑战是：

（1）鲁棒性问题：SfM方法鲁棒性较差，易受到光线、噪声、模糊等问题的影响，而且在匹配过程中，如果出现了误匹配问题，可能会导致结果精度下降。

（2）完整性问题：SfM方法在重建过程中可能由于丢失信息或不精确的信息而难以校准图像，从而不能完整地重建场景结构。

（3）运算量问题：SfM方法目前存在的主要问题就是运算量太大，导致三维重建的时间较长，效率较低。

（4）精确性问题：目前SfM方法中的每一个步骤，如相机标定、图像特征提取与匹配等一直都无法得到最优化的解决，导致了该方法易用性和精确度等指标无法得到更大提高。

针对以上这些问题，在未来一段时间内，SfM方法的相关研究可以从以下几个方面展开：

（1）改进算法：结合应用场景，改进图像预处理和匹配技术，减少光线、噪声、模糊等问题的影响，提高匹配准确度，增强算法鲁棒性。

（2）信息融合：充分利用图像中包含的各种信息，使用不同类型传感器进行信息融合，丰富信息，提高完整度和通用性，完善建模效果。

（3）使用分布式计算：针对运算量过大的问题，采用计算机集群计算、网络云计算以及GPU计算等方式来提高运行速度，缩短重建时间，提高重建效率。

（4）分步优化：对SfM方法中的每一个步骤进行优化，提高方法的易用性和精确度，使三维重建的整体效果得到提升。

4 结语

计算机视觉三维重建技术在近年来的研究中取得了长足的发展，其应用领域涉及工业、军事、医疗、航空航天等诸多行业。但是这些方法想要应用到实际中都还要更进一步的研究和考察。计算机视觉三维重建技术还需要在提高鲁棒性、减少运算复杂度、减小运行设备要求等方面加以改进。因此，在未来很长的一段时间内，仍需要在该领域做出更加深入细致的研究。

参考文献

[1]Tomasi C， Kanade T. Shape and motion from image streams： a factorization method - full report on the orthographic case[J]. International Journal of Computer Vision， 1992， 90（21）： 9795-9802.

[2]Morevec H P. Towards automatic visual obstacle avoidance[C].// Proc of the 5th International Joint Conference on Artificial Intelligence， 1977： 584.

[3]Harris C. A combined corner and edge detector[C].// Proc of Alvey Vision Conference， 1988： 147-151.

[4]Smith S M， Brady J M. SUSAN： a new approach to low level image processing[J]. International Journal of Computer Vision， 1997， 23（1）： 45-78.

[5]Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision，2004，60（60）：91-110.

[6]Bay H， Ess A， Tuytelaars T， et al. Speeded-up robust features （SURF）[J]. Computer Vision and Image Understanding，2008，110（3）：346-359.

[7]Grauman K， Darrell T. Pyramid match hashing： Sub-linear time indexing over partial correspondences[C].// Proc of IEEE Conference on Computer Vision and Pattern Recognition， 2007： 1-8.

[8]Mount D M， Arya S. ANN： A library for approximate nearest neighbor searching[C].// Proc of The 14th Annual ACM-SIAM Symposium on Discret Algorithms， 2010.

[9]Longuet-Higgins H C. A computer algorithm for reconstructing a scene from two projections[J]. Nature， 1981， 293（5828）： 133-135.

[10]Luong Q T. Matrice fondamentale et autocalibration en vision par ordinateur[J]. Paris， 1992.

[11]Ni K， Steedly D， Dellaert F. Out-of-Core bundle adjustment for large-scale 3D reconstruction[C].// Proc of IEEE International Conference on Computer Vision， 2007： 1-8.

[12]Engels C， Stewénius H， Nistér D. Bundle adjustment rules[C].// Proc of Symposium on Photogrammetric Computer Vision， 2006： 266-271.

[13]Lourakis M I A， Argyros A A. SBA： a software package for generic sparse bundle adjustment[J]. Acm Transactions on Mathematical Software， 2009， 36（1）： 26-30.

[14]Lhuillier M， Quan L. A quasi-dense approach to surface reconstruction from uncalibrated images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2005， 27（3）： 418-433.

[15]Furukawa Y， Ponce J. Accurate， dense， and robust multiview stereopsis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2010， 32（8）： 1362-1376.