改进布谷鸟算法在成败型产品可靠性抽样检验方案设计中的应用研究
2017-04-25郭志明李长福姬广振刘勤钱云鹏胡冰甦
郭志明, 李长福, 姬广振, 刘勤, 钱云鹏, 胡冰甦
(中国兵器科学研究院, 北京 100089)
改进布谷鸟算法在成败型产品可靠性抽样检验方案设计中的应用研究
郭志明, 李长福, 姬广振, 刘勤, 钱云鹏, 胡冰甦
(中国兵器科学研究院, 北京 100089)
成败型产品可靠性抽样检验方案设计一直是可靠性试验领域亟待解决的问题之一,使用元启发式算法进行求解是一种新思路。布谷鸟算法是近年来提出的一种新颖的元启发式算法,以其简单高效而获得了广泛应用。提出了以风险距离为目标的成败型产品可靠性抽样检验方案设计模型,之后对标准布谷鸟算法的机理进行了阐述,并针对算法局部寻优能力差的问题,提出了一种两阶段发现概率方法来协调算法的全局搜索能力和局部搜索能力,最后结合具体的算例验证了该方法的可行性和有效性。
兵器科学与技术; 改进布谷鸟算法; 可靠性抽样检验方案; 成败型产品; 风险距离; 整数优化
0 引言
抽样检验是一种特殊的假设检验,它是按生产方和使用方所协商的要求,用统计方法制定试验方案对一批产品进行抽样检验,根据检验结果对这批产品做出接收和拒收的判断[1]。在抽样检验中,每次使用都相互独立,且对于试验结果只有成功、失败两种情况的产品称为成败型产品,火炸药、导弹和运载火箭等都属于成败型产品。目前,成败型产品抽样方案的设计是从国家标准GB5080.5—85《设备可靠性试验成功率的验证试验方案》中查取与生产方和使用方要求最接近的方案,但国家标准GB5080.5—85中只给出了双方风险α=β=5%,α=β=10%,α=β=20%,α=β=30%这4种情况的最优方案[2],而实际中风险还可能取其他值,如6%、15%、18%等,甚至α和β并不相等,这使得该标准在应用过程中具有一定的局限性。
成败型产品抽样检验方案是由n、Ac两个数决定(产品批量较大时),其中n是抽取的样本量,Ac是合格判定数。可靠性抽样检验方案设计在本质上是带约束的整数优化问题,目前仍无普遍的解析方法可以进行精确求解,若采用遍历法对n和Ac进行遍历,则需要遍历n×Ac次,效率非常低,如果n取5 000,Ac取40,则需要遍历2×105次。文献[3]在考虑双方风险的成败型定数截尾抽样模型的基础上,运用证据理论方法,研究了基于研制信息的测试性验证试验方案,并在测试性验证中取得了良好效果。文献[4]提出对抽样方案方程组进行等价变形,并设计相关算法进行求解,但其算法过程相对繁琐。文献[5]构建了风险选择的准则方程,但需结合实际对准则方差进行分类讨论,过程较复杂。这些研究方法过程复杂繁琐,仍不能有效简化方案设计的求解过程。因此,建立一种通用的成败型产品可靠性抽样检验方案设计模型,并设计出能够高效求解模型的算法,从而使方案设计过程变得简单快捷已经迫在眉睫。
布谷鸟算法是一种新的无约束优化方法,具有简单、参数少、易于实现等优点,而且其性能接近于标准的粒子群优化算法和差分演化算法[6],成为继遗传算法和粒子群算法之后启发式算法的新亮点[7]。与遗传算法、粒子群算法、蚁群算法等算法相比,布谷鸟算法在参数设置、全局搜索能力、通用性和鲁棒性方面具有综合性优势,布谷鸟算法作为后起之秀,它的优越性使其广泛应用于各个研究领域[8-11]。作为一种高效新颖的优化算法,布谷鸟算法在大型复杂可靠性优化体系、结构可靠性设计分析、冗余分配、可靠性增长等可靠研究领域都有学者做过相关研究,但布谷鸟算法还尚未被引入到可靠性抽样检验方案设计中,事实上,凡是可以归结为优化的可靠性工程问题都可以尝试采用布谷鸟算法进行求解。本文首先建立了抽样检验方案设计模型,之后对标准布谷鸟算法的机理进行了阐述,并针对算法局部寻优能力差的问题,提出了一种两阶段发现概率方法来协调算法的全局搜索能力和局部搜索能力,并将改进的算法应用到了抽样方案设计中。
1 成败型产品抽样检验方案设计模型
1.1 问题的提出
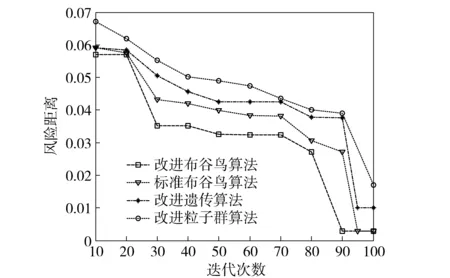
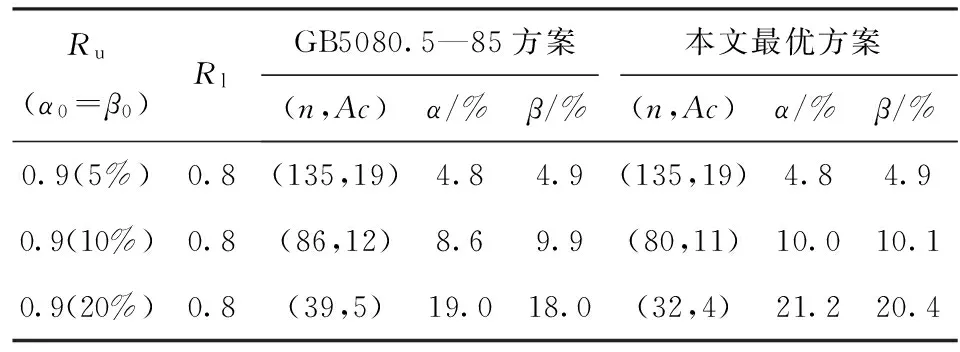
成败型产品抽样检验方案的设计过程:从批量为N的一批产品中随机抽取n件产品进行检验,假设检验出不合格品数为d,那么当d小于等于Ac时,接收该批产品,否则拒收,通常把这样一个检验方案记为(N,n,Ac),其中N为已知量,只要确定出n与Ac,也就确定了抽样检验的方案。当N相对于n来讲比较大时,批量N的影响就不大,所以在这种条件下可以将抽样检验方案记为(n,Ac),显然有Ac 图1 成败型产品抽样检验流程图Fig.1 Flow chart of sampling inspection program for success or failure products 抽样检验方案中存在两类风险:生产方风险α和使用方风险β. 生产方风险是把产品合格批判定为不合格批的概率,使用方风险是把不合格批判定为合格批的概率。α和β计算方法[12]为 (1) 式中:Ru是可靠度检验上限;Rl是可靠度检验下限。 在方案设计的过程中,双方都希望自己的风险尽量低,但理论研究表明,要使α小必导致β大,要使β小必导致α大,设计一个能够平衡双方风险的方案对双方都很重要。在实际中,生产方和使用方首先根据检验上限和检验下限协定一个双方都能接受的额定风险α0(生产方额定风险)和β0(使用方额定风险),之后通过比较权衡得出方案。 1.2 目标函数 在抽样方案设计过程中生产方希望α越低且与α0越接近越好;而使用方希望β越低且与β0越接近越好,双方都希望自己的风险尽可能接近额定风险,因此,抽样方案设计过程也就是双方风险平衡博弈的过程,目标函数不能只考虑某一方风险与额定风险距离最小,应既要考虑α与α0接近,又要保证β与β0越接近,本文以双方各自的风险与额定风险(最优解)的风险距离最小为目标函数,定义为 (2) 风险距离采用的是欧式距离,欧式距离反映的是真实距离,这样可以使方案设计比较客观,使双方都能接受。 从(2)式中可以看出,α与β对目标函数的贡献率是一样的,这表明生产方和使用方风险同等重要。 1.3 约束条件 以n=500,Ac=40为例,做出样本量、合格判定数对风险距离的响应面以及样本量- 合格判定数剖面视图,如图2所示。 图2 样本量、合格判定数和风险响应面图Fig.2 Response surface of sample size, acceptance number and risk distance 通过观察图2(a)可以发现,优质可行解就集中在一个很窄的区域内。理论上做出如下分析:若边界点估计值(1-Ac/n)小于下限值,则使用方风险β会变大,则方案(n,Ac)落在图2(b)左上方红色区域中,风险差比较大,显然使用方不能满意;若边界点估计值大于上限值,则生产方风险α过大,此时方案(n,Ac)落在右下方红色区域中,显然生产方不能满意。而当边界点估计值处于检验上限和检验下限之间,即落在图2(b)中三角形蓝色区域时,双方风险差才变小,才可能使风险距离得到平衡。根据以上分析,将Ac取值范围确定为 n(1-Ru)≤Ac≤n(1-Rl). (3) 1.4 优化模型 综合前述分析,以风险距离为目标的成败型产品可靠性抽样检验方案设计模型为 (4) 式中:nmax为最大抽样样本容量。该模型是一个整数优化模型,利用传统方法难以求解且耗时较长,近年来随着群元启发式算法的发展,许多学者运用遗传算法、蚁群算法、粒子群算法等方法进行求解,本文尝试采用布谷鸟算法来求解该模型。 2009年,剑桥大学的Yang和拉曼工程大学的Deb模拟布谷鸟的寻窝产卵行为,提出一种新的智能优化算法——布谷鸟搜索算法[13]。布谷鸟算法属于元启发式算法,具有元启发式框架的智能算法,启发式算法的求解都有如(5)式的迭代方程 Xi+1←Xi+sδx, (5) 式中:δx代表步长;s代表比例系数;Xi代表上一代可行解;Xi+1代表更新后的可行解。 2.1 标准布谷鸟算法 布谷鸟是典型的巢寄生鸟类,即把自己的蛋产到其他鸟类的鸟巢中,让鸟巢的主人孵化养育布谷鸟。为了降低自己的鸟蛋被寄居的鸟巢主人发现的概率,布谷鸟会把它们自己的蛋产于相似的鸟类窝中,但仍可能被鸟巢的主人发现,当鸟巢的主人发现有布谷鸟蛋在自己的鸟巢时,就把布谷鸟蛋毁坏或者丢弃自己的鸟巢,然后重新建巢。把布谷鸟巢寄生繁殖机理形成理论,可以设计出布谷鸟算法,简单说来可以使用以下3个理想化的规则: 1)每只布谷鸟一次产一个卵,并随机选择寄生巢来孵化它; 2)在随机选择的一组寄生巢中,最好的寄生巢将会被保留到下一代; 3)可利用的寄生巢数量是固定的,一个寄生巢的主人能发现一个外来鸟蛋的概率为pa. 布谷鸟算法新解的更新采用莱维飞行策略,莱维飞行二维坐标示意图如图3所示。从中不难看出,莱维飞行的特点是在飞行中可以意外地90°转弯,这样飞行可以使动物更有效地搜索到食物。莱维飞行不仅适用于动物界和昆虫界,在人类社会的某些活动(如市场价格波动、打猎等)也符合莱维飞行的特性。采用莱维飞行策略的解的迭代方程[14]为 pj+1=pj+randn[D]stepsizej, (6) 式中:pj代表上一代可行解;pj+1代表更新后的可行解;randn[D]为比例系数,值为区间[1,D]上的一个均匀分布的随机数,D默认取约束变量的个数;stepsizej为步长,由(7)式[14]确定: (7) 式中:ω为常数,用于控制步长大小,默认取0.01;υ=randn[D] ;u=δrandn[D],δ由(8)式确定[14];pbest为当前最优解。 (8) 式中:q为常数,默认取3/2. 图3 莱维飞行示意图Fig.3 Path of Lévy flight 如果布谷鸟蛋被外来鸟发现,则布谷鸟迁徙策略[14]为 pj+1=pj+rand(pj,r1-pj,r2), (9) 式中:rand为(0,1)区间内服从均匀分布的随机数;pj,r1和pj,r2为第j代的两个随机解。每次迭代产生新的鸟巢位置后,将鸟巢主人发现布谷鸟蛋的概率pa与随机产生的一个随机数r~U(0,1)进行比对,若r>pa,则按(9)式进行位置更新,否则解保持不变。 2.2 算法的改进 布谷鸟算法是一种无约束的搜索技术,因此它缺乏明确的约束处理机制,这使得它在处理有约束优化问题时比较困难,此外,布谷鸟算法虽然具有较好的全局性能,但却在收敛速度和局部搜索能力上有所欠缺。目前国内外学者对布谷鸟算法的改进主要涉及以下三方面:发现概率、步长以及和其他算法的混合[15-19]。本文主要从以下两方面对标准布谷鸟算法进行改进:1)增加约束处理机制及离散化处理方法;2)两阶段动态发现概率法取代原固定发现概率,第一阶段注重全局搜索,第二阶段注重局部搜索,使算法的全局搜索与局部搜索能力得到更好的平衡。 2.2.1 约束条件处理机制 约束优化问题处理方法可分为直接法和间接法两类,直接法通常是基于梯度的搜索方法,如投影梯度法、简约梯度法、可行方向法等,但求解需要设置很好的初值点且需要函数的梯度信息,对于不可导、可行域不连通等问题无能为力[20]。间接法主要有惩罚函数法、消元法和拉格朗日乘子法。罚函数法因其简单易实现成为一种被广泛运用的约束处理技术,其基本思想是通过增加惩罚项将约束问题转化为无约束问题。考虑到罚函数法具有简单、实用和高效的特点,本文采用罚函数法来处理模型(4)式,形式如(10)式所示: (10) 式中:F(n,Ac)为新的目标函数;f(n,Ac)为风险距离;d1和d2为惩罚系数;sv表示所有违反约束值的总和,nv表示违反约束的数目。 抽样方案中有两个变量n和Ac,模型中对这两个量的约束为必须是正整数。由(3)式可知n和Ac具有伴随关系,即Ac的取值范围是由n决定的,因此可首先对n进行约束处理,再由n生成Ac. 对n的约束处理是确保n为区间[1,nmax]的整数,分两步实现:先用均匀分布生成连续的n,再对n进行取整,如(11)式所示: n=round(Lb+(Ub-Lb)×rand), (11) 式中:round()为取整运算;Lb为n的取值下限;Ub为n的取值上限;rand为[0,1]区间内服从均匀分布的随机数。 通过(11)式确保n满足约束条件后,再对Ac进行处理,确保Ac为区间[(1-Ru)×n, (1-Rl)×n]的整数。设[(1-Ru)×n, (1-Rl)×n]区间内的整数点为m个,则Ac按等概率在m个点中进行选择,即 P{Ac|Ac∈[(1-Ru)×n,(1-Rl)×n]的整数}= (12) 所有Ac按(12)式随机生成就能保证其满足约束条件,需要注意的是在求解过程中并不是对所有自变量都执行莱维飞行,而是只需对n进行处理即可,原因是莱维飞行具有较强的随机性,若同时对n和Ac进行莱维飞行,则很容易产生Ac不满足约束条件的情况。 2.2.2 全局搜索能力和局部搜索能力的平衡 由于莱维飞行具有较强的随机性,这使得布谷鸟算法具有很好的全局性能,但也使布谷鸟算法在收敛速度和局部搜索能力上有所欠缺。布谷鸟算法中,pa是非常重要的参数,可以理解为父代个体被保留的概率,良好的pa值可以平衡算法的全局和局部搜索能力。为此,将算法求解过程分为两个阶段:第一阶段重全局轻局部,让布谷鸟很容易被发现,从而迫使布谷鸟去寻求新的巢穴;第二阶段轻全局重局部,使布谷鸟不容易被发现,使得布谷鸟在当前巢穴位置附近寻找更优的巢穴。实现方法:在算法前Nmax/2(Nmax为最大迭代次数)次迭代中pa逐渐减小,让布谷鸟飞出去开辟新的巢穴,pa采用负正弦自适应递减策略;而在后Nmax/2次迭代中让布谷鸟在当前区域修养生息,pa采用负余弦自适应递增策略。以上计算策略如(13)式所示: (13) 式中:pa,min和pa,max分别表示发现概率的最小和最大值;Ni为当前迭代次数( 1≤Ni≤Nmax)。 综上所述,改进后的布谷鸟算法流程如图4所示。 图4 改进的布谷鸟算法流程图Fig.4 Flow chart of improved cuckoo search algorithm 某车载智能弹药需要进行批次检验,其中批量N= 10 000,抽样的最大样本量nmax不超过500(批量较大),合同中规定的可靠度指标要求为Ru=0.9,Rl=0.8,经协商确定生产方和使用方风险分别为α0=10%和β0=15%,则可靠性抽样检验方案模型为 (14) 采用本文提出的改进布谷鸟算法对模型进行求解,并将改进遗传算法[21]、改进粒子群算法[22]和标准布谷鸟算法作为对比,为了使对比结果如实反映算法的搜索能力,4个算法的种群规模均设置为25,最大迭代次数设置为100.由于这些算法都属于随机搜索方法,结果不确定,因此以程序独立运行10次目标函数的平均值作为对比参数。首先通过遍历法找到最优方案为n=64,Ac=9,生产方风险α=10.3%,使用方风险β=15.0%,目标函数值为0.002 81,作为参照。然后将各个算法运行10次,并求出目标函数的平均值和标准差,列于表1中。 从表1中可以看出,改进布谷鸟算法能够找到全局最优解,目标函数均值比改进遗传算法和改进粒子群算法相比较优,标准差与二者相比也相对较低,表明解的质量和稳定性都有提高。标准布谷鸟算法在100次寻优过程中未找到最优解,说明对pa的改进设置有效,虽然改进粒子群算法找到了全局最优解,但标准差要比改进布谷鸟算法大。总体而言,与上述3种算法相比,改进布谷鸟算法优化结果较好且相对稳定,算法性能仿真如图5所示。 从图5中可以看出,在相同迭代次数下,采用了两阶段动态发现概率法的改进布谷鸟算法能找到最优解,且收敛速度较快。粒子群算法也找到最优解,但是收敛速度相对较低,标准布谷鸟算法虽然收敛了,但不是全局最优,表明标准布谷鸟算法陷入了局部最优,而遗传算法由于迭代次数偏低未收敛。此外对比几种算法的复杂度可知,改进布谷鸟算法未增加算法复杂度。相对于另3种算法,改进布谷鸟算法的搜索能力得到了提升,证明本文的改进策略有效。 表1 不同优化算法结果对比 注:T0、Tg分别表示个体极值和全局极值需要扰动的停滞步数阈值。 图5 算法性能比较图Fig.5 Comparison of algorithm performances 此外,为了验证本文提出模型的合理性,取3组双方风险相同的情况:α0=β0=5%,α0=β0=10%,α0=β0=20%,然后将采用本文方法设计的最优抽样检验方案与国家标准GB5080.5—85中的方案进行对比,结果列于表2中。 从表2可以看出:当额定风险为5%时,本文的方案与GB5080.5—85方案相同;当额定风险为10%时,本文方案的α为10%,等于额定风险,β为10.1%,与额定风险相差1%,GB5080.5—85方案中α为8.6%,与额定风险相差14%,β为9.9%,与额定风险差1%;额定风险为20%时,本文方案的α和β分别与额定风险相差6%、2%,GB5080.5—85方案的α和β与额定风险分别相差5%、10%;本文方案比GB5080.5—85方案更接近额定风险,且试验样本量均不高于GB5080.5—85,从而降低了试验成本,说明了本文模型的先进性。 表2 本文最优方案与GB5080.5—85方案对比 成败型产品可靠性抽样检验方案设计的关键是如何平衡生产方和使用方的风险,本文提出的以风险距离为目标的可靠性抽样检验方案优化模型能够准确地量化描述该问题,使方案设计的过程可量化,避免了以往只能采用尝试法的问题。提出了改进的布谷鸟算法,使其全局搜索能力和局部搜索能力得到平衡。算例的结果表明:改进的布谷鸟算法能够解决本文的整数优化模型,相比较其他算法更容易找到最优解,且计算结果相对较稳定,为解决成败型产品可靠性抽样检验方案设计问题提供了一条新途径。 如何从算法机理上进一步提高布谷鸟算法求解成败型产品可靠性抽样检验方案设计模型的适用性和高效性是下一步的研究重点。 References) [1] 茆师松,汤银才,王玲玲. 可靠性统计[M]. 北京:高等教育出版社,2008. MAO Shi-song, TANG Yin-cai, WANG Ling-ling. Reliability statistics [M]. Beijing: Higher Education Press, 2008. (in Chinese) [2] 国家标准局. GB5080.5—85 设备可靠性试验成功率的验证试验方案[S].北京:中国标准出版社,1985. National Bureau of Standards. GB5080.5—85 Equipment reliability testing compliance test plans for success ratio [S]. Beijing: China Standards Press, 1985. (in Chinese) [3] Chang C, Yang J, Cao P. Study on the scheme of testability de-monstration test based on development information[J]. Hangkong Xuebao/Acta Aeronautica Et Astronautica Sinica, 2012, 33(11):2057-2064. [4] 李晓阳,姜同敏,肖良华. 成败型一次抽样检验方案算法的等价变形[J]. 北京航空航天大学学报,2005,31(8):904-907. LI Xiao-yang, JIANG Tong-min, XIAO Liang-hua. Development algorithm of single sampling inspection plan of pass-fail experiment [J]. Journal of Beijing University of Aeronautics and Astronautics, 2005,31(8):904-907. (in Chinese) [5] 杜旭,王卓健,马涛,等. 考虑双方风险的定数截尾抽样方案算法优化[J]. 火力与指挥控制,2015,40(8):52-55. DU Xu, WANG Zhuo-jian, MA Tao, et al. Optimization algorithm of Type-II censoring of considering both sides risk inspection plan of pass-fail experiment [J]. Fire Control & Command Control, 2015, 40(8): 52-55. (in Chinese) [6] 王李进,尹义龙,钟一文. 逐维改进的布谷鸟搜索算法[J]. 软件学报,2013,24(11):2687-2698. WANG Li-jin, YIN Yi-long, ZHONG Yi-wen. Cuckoo search algorithm with dimension by dimension Improvement [J]. Journal of Software, 2013, 24(11): 2687-2698. (in Chinese) [7] Bhargava V, Fateen S. Cuckoo search: a new nature-inspired optimization method for phase equilibrium calculations [J]. Fluid Phase Equilibria, 2013, 337: 191-200. [8] 黄继达. 布谷鸟算法的改进及其应用研究[D]. 武汉:华中科技大学,2014. HUANG Ji-da.Research on cuckoo search and its applications[D]. Wuhan: Huazhong University of Science and Technology, 2014. (in Chinese) [9] 兰少峰,刘升. 布谷鸟搜索算法研究综述[J]. 计算机工程与设计,2015,36(4):1063-1067. LAN Shao-feng, LIU Sheng. Overview of research on cuckoo search algorithm [J]. Computer Engineering and Design,2015, 36(4): 1063-1067. (in Chinese) [10] 陶涛,张俊,信昆仑,等. 基于布谷鸟算法的给水管网调压阀优化设计[J]. 同济大学学报:自然科学版,2016,44(4):600-604. TAO Tao, ZHANG Jun, XIN Kun-lun, et al. Optimal valve control in water distribution systems based on cuckoo search [J]. Journal of Tongji University: Natural Science, 2016, 44(4): 600-604. (in Chinese) [11] 薛浩然,张珂珩,李斌,等. 基于布谷鸟算法和支持向量机的变压器故障诊断[J]. 电力系统保护与控制,2015,43(8):8-13. XUE Hao-ran, ZHANG Ke-heng, LI Bin, et al. Fault diagnosis of transformer based on the cuckoo search and support vector machine [J]. Power System Protection and Control, 2015, 43(8):8-13. (in Chinese) [12] 何国伟. 可靠性试验技术[M]. 北京:国防工业出版社,1996. HE Guo-wei. Reliability test technology [M]. Beijing: National Defense Industry Press, 1996. (in Chinese) [13] Civicioglu P, Besdok E. A conceptual comparison of the cuckoo-search, particle swarm optimization, differential evolution and artificial bee colony algorithms[J]. Artificial Intelligence Review, 2013, 39(4):315-346. [14] Yang X S, Deb S. Cuckoo search via Lévy flights [C]∥Proceedings of World Congress on Nature & Biologically Inspired Computing. India: IEEE, 2009:210-214. [15] 屈迟文,傅彦铭,戴俊. 基于改进CS优化算法的灰色神经网络预测模型[J]. 西南师范大学学报: 自然科学版,2014,39(1):131-136. QU Chi-wen, FU Yan-ming, DAI Jun. On a forecasting model of grey neural network based on improved cuckoo search optimal algorithm [J]. Journal of Southwest China Normal University: Natural Science Edition, 2014, 39(1):131-136. (in Chinese) [16] 秦强,冯蕴雯,薛小锋. 改进布谷鸟算法在结构可靠性分析中的应用[J]. 系统工程与电子技术,2015, 37(4):979-984. QIN Qiang, FENG Yun-wen, XUE Xiao-feng.Improved cuckoo search algorithm for structural reliability analysis [J]. Systems Engineering and Electronics, 2015, 37(4):979-984. (in Chinese) [17] 李东生,高杨,雍爱霞. 基于改进离散布谷鸟算法的干扰资源分配研究[J]. 电子与信息学报, 2016, 38(4):899-905. LI Dong-sheng, GAO Yang, YONG Ai-xia. Jamming resource allocation via improved discrete cuckoo search algorithm[J]. Journal of Electronics & Information Technology, 2016, 38(4):899-905. (in Chinese) [18] Valian E, Mohanna S, Tavakoli S. Improved cuckoo search algorithm for feed-forward neural network training [J]. International Journal of Artificial Intelligence & Applications, 2011, 2(3): 36-43. [19] Valian E, Tavakoli S, Mohanna S, et al. Improved cuckoo search for reliability optimization problems[J]. Computers & Industrial Engineering, 2013, 64(1):459-468. [20] 王勇,蔡自兴,周育人,等. 约束优化进化算法[J]. 软件学报,2009,20(1):11-29. WANG Yong, CAI Zi-xing, ZHOU Yu-ren, et al. Constrained optimization evolutionary algorithms [J]. Journal of Software, 2009, 20(1): 11-29. (in Chinese) [21] 耿飞,龙海辉,赵健康,等. 基于改进遗传算法的传感器优化配置[J]. 计算机仿真,2014,31(5):56-59. GENG Fei, LONG Hai-hui, ZHAO Jian-kang, et al. Sensor optimization method based on improved genetic algorithm [J]. Computer Simulation, 2014, 31(5):56-59. (in Chinese) [22] 胡旺,李志蜀. 一种更简化而高效的粒子群优化算法[J]. 软件学报,2007,18(4):861-868. HU Wang, LI Zhi-shu. A simpler and more effective particle swarm optimization algorithm [J].Journal of Software, 2007, 18(4): 861-868. (in Chinese) Improved Cuckoo Search Algorithm for Reliability Sampling Inspection Program in Binomial Case GUO Zhi-ming, LI Chang-fu, JI Guang-zhen, LIU Qin, QIAN Yun-peng, HU Bing-su (Ordnance Science and Research Academy of China, Beijing 100089, China) The design of reliability sampling inspection program for the success or failure products is an issue to be solved in reliability test. Meta-heuristic algorithm provides a new idea to solve the problem. Cuckoo search algorithm is a new meta-heuristic algorithm, and has been widely used in many fields because of its simplicity but efficiency. A model for reliability sampling inspection program is developed to minimize the risk. The mechanism of the cuckoo search algorithm is expounded. For the local search efficiency of the algorithm, an adaptive detection probability is proposed to balance the global search and local search efficiencies. The result of a case study reveals that the proposed method is feasible and effective. ordnance science and technology; improved cuckoo search algorithm; reliability sampling inspection program; success or failure product; distance of risk; integer optimization 2016-08-05 武器装备预先研究项目(51319010210) 郭志明(1985—),男,工程师。E-mail:gzmnwpu@163.com TB114.37 A 1000-1093(2017)04-0758-08 10.3969/j.issn.1000-1093.2017.04.018

2 改进的布谷鸟算法

1/m.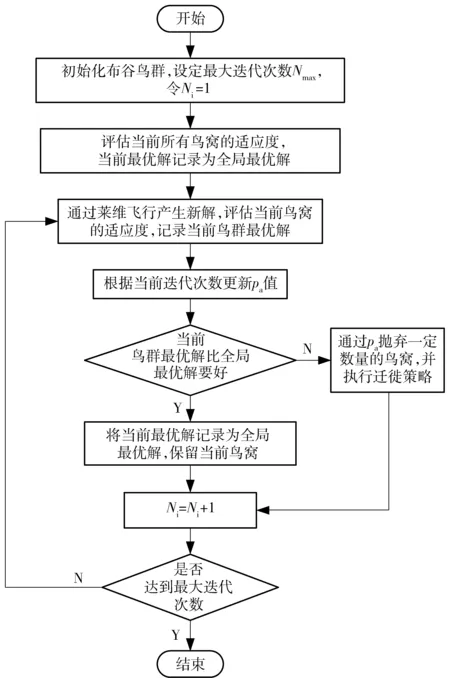
3 算例分析

4 结论
