变体飞行器故障检测与容错控制一体化设计
2017-04-25程昊宇董朝阳江未来王青隋晗
程昊宇, 董朝阳, 江未来, 王青, 隋晗
(1.北京航空航天大学 航空科学与工程学院, 北京 100083; 2.湖南大学 电气与信息工程学院, 湖南 长沙 410082;3.北京航空航天大学 自动化科学与电气工程学院, 北京 100083)
变体飞行器故障检测与容错控制一体化设计
程昊宇1, 董朝阳1, 江未来2, 王青3, 隋晗1
(1.北京航空航天大学 航空科学与工程学院, 北京 100083; 2.湖南大学 电气与信息工程学院, 湖南 长沙 410082;3.北京航空航天大学 自动化科学与电气工程学院, 北京 100083)
针对一类后掠翼可变的变体飞行器,考虑同时存在状态时滞和随机丢包的网络环境,基于切换系统理论,研究了变体飞行器闭环故障检测滤波器的设计问题。将变体飞行器建模成以高度、马赫数和后掠角为参变量的切换系统。为了保证系统能够有效检测出系统故障并且跟踪指令信号,基于一体化方法,设计基于模态依赖观测器的故障检测滤波器和基于残差估计的输出容错控制器。通过多Lyapunov-Krasovskii函数方法和平均驻留时间方法分析系统在异步切换情况下的稳定性。以线性矩阵不等式的形式给出满足给定性能指标滤波器和控制器存在的充分条件。通过仿真验证了所提方法能够有效检测出故障,输出信号能够准确跟踪指令信号,且在不确定情况下具有较好的鲁棒性。
兵器科学与技术; 变体飞行器; 故障检测; 容错控制; 异步切换
0 引言
变体飞行器[1-2]能够在飞行过程中根据飞行参数、任务模式和外部飞行环境等因素的变化主动调整外形结构,从而改善自身的气动性能和操纵性能,达到扩大飞行包线和满足多任务模式飞行要求的目的。但是,飞行器外形的改变会导致其后掠角、机翼面积和机翼展长等构型参数发生变化,从而引起气动力和气动力矩等参数的非线性变化,给飞行器的建模和控制器设计带来了很多的挑战。近年来,变体飞行器的建模、控制与仿真吸引了众多学者的兴趣。
切换系统理论是研究参数大范围变化复杂不确定系统的重要方法,在工业控制、航空航天和机器人控制等领域获得了广泛的应用[3-9]。文献[5]将切换总次数、切换时刻次序作为代价函数,利用遗传算法分析了子系统与系统总体稳定性和动态性能之间的关系。文献[6,8]则利用Lyapunov函数方法分析了切换系统的稳定性,并将结果应用于多自由度机器人和倾斜旋翼机的系统设计中,获得了良好的效果。
另一方面,由于现代飞行器各个部件之间的通信是通过网络实现的,网络的引入具有结构灵活,可扩展性好等优点,但是由于网络带宽和信道容量有限,导致产生时延[10]和数据包丢失[11-12]的现象,引起系统性能下降甚至引发故障。因此,为了保证飞行器的飞行性能,需要对其故障检测问题[13]进行研究。文献[14]针对Takagi-Sugeno模糊模型,设计了基于观测器的故障检测滤波器,将故障检测问题转化为H_/H∞滤波问题,并以线性矩阵不等式(LMI)的形式给出了滤波器存在的充分条件和求解方法。文献[15]针对存在数据包丢失的离散切换系统,设计了模态依赖滤波器,保证了系统在存在丢包的情况下依然能够有效检测出故障。上述文献均假设没有控制器或者控制器已经设计好,但是在实际系统中,故障检测性能会随着输出跟踪性能的下降而下降;控制器也需要利用故障检测的结果。二者性能之间会相互影响,滤波器和控制器分开设计的方法无法保证系统全局最优。为了获得理想的系统性能,需要重复进行设计。为了简化设计步骤,保证系统性能,闭环故障检测引起了学者的广泛关注[16-19]。文献[16]采用一体化设计思路进行滤波器和控制器的设计,避免了重复设计问题,保证了系统的稳定性,但是没有考虑控制器对信号的跟踪问题。文献[17]对大包线飞行器进行了闭环故障检测滤波器的设计,避免了反复设计,保证了滤波器和控制器的性能。
由于目前对变体飞行器的分析和设计主要集中在建模和控制器设计,对于其故障检测问题还鲜有报道。飞行器网络中存在着状态时滞和丢包现象,会引起控制器/滤波器的切换滞后于系统状态的切换,控制器/滤波器与子系统模态存在着匹配区间和不匹配区间,在不匹配区间系统能量增加,即导致异步切换现象[20]。另一方面,当飞行器系统受到外界故障干扰或者工作状态发生变化时,时滞和丢包现象会导致传感器测量到的信号不能及时反馈至控制器和执行机构,故障检测和控制系统不能准确、及时地应对故障信号和扰动,使得变体飞行器性能下降。变体飞行器在大包线飞行过程中构型可能会发生变化,因此需要保证良好的性能和控制精度,在出现故障情况时能够迅速检测出故障,并保持稳定性和给定的性能指标。因此,本文开展了对存在时滞和丢包的变体飞行器故障检测和容错控制问题的研究。设计基于观测器的故障检测滤波器和基于状态估计的输出容错控制器。采用多Lyapunov-Krasovskii函数方法和平均驻留时间方法保证系统稳定并具有给定的性能。以LMI的形式给出了滤波器和控制器的存在条件和求解方法。最后通过仿真验证了本文所提方法的有效性,保证了变体飞行器能够快速、有效检测出故障,并且在故障情况下仍然能够有效跟踪指令信号。
1 变体飞行器建模
本文选择美国NextGen公司设计的一款后掠角可变无人技术验证机“火蜂”(Fire-bee)为研究对象。“火蜂”在飞行过程中能够通过变化后掠角ξ,实现“巡航”和“高速”构型间的切换。机翼后掠角机翼后掠角可以在15 °~60 °内变化。ξ=15 °为巡航构型机翼后掠角;ξ=60 °对应高速构型机翼后掠角。平均气动弦长、机翼面积等物理量均随后掠角变化而变化,表1中的数据为变体飞行器在“巡航”和“高速”构型下的参数。

表1 变体飞行器结构参数
建立变体飞行器的纵向短周期非线性动力学模型:
(1)
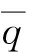
(2)
对系统(1)式在平衡点处进行线性化,可以得到在平衡点附近的线性小扰动模型:
(3)

(4)
式中:i∈Ω,i为三维包线内的工作点标号,Ω为工作点标号全集;ω(t)、f(t)分别为L2范数有界的外界扰动信号和故障信号;Ac,i、Bc,i、Cc,i、Dc,i、Fc,i表示在不同特征点处系统的适维常值实矩阵。
随着现代飞行器各个子系统,各个功能模块之间需要交换的数据成倍增加,对系统的灵活性、智能性和可维修性的要求大大增加。传统点对点的数据传输模式不再适用,因此在现代飞行器一般通过总线网络实现信息的传递与共享,网络环境下变体飞行器系统如图1所示。

图1 变体飞行器故障检测系统结构图Fig.1 Structure diagram of fault detection system for morphing aircraft
本文考虑网络传输的特点,对系统作如下合理假设:
假设1 控制器和故障检测单元位于变体飞行器飞控机内部,传感器挂接在总线网络上,与变体飞行器飞控机系统形成闭合回路,执行机构与飞控机直接连接。
假设2[15]传感器采用时间驱动,采样周期为T. 控制器和执行机构采用事件驱动。数据传输方式为单包传输,丢包存在于传感器- 控制器链路,且丢包服从丢包率为ρ的Bernoulli随机过程。定义随机变量θ(k)∈{0,1},θ(k)=1表示数据传输正常,θ(k)=0表示数据传输失败,且满足:
式中:Prob{·}表示事件的概率;E{·}为事件的期望;Var{·}为事件的方差。
具有状态时滞,变体飞行器在工作点i处的离散线性模型:
(5)

当传感器- 控制器链路发生丢包时,

(6)
本文采用(7)式所示的故障检测滤波器产生残差信号:
(7)
为了使得输出信号能够跟踪范数有界指令信号h(k),定义输出跟踪误差信号为

(8)
故输出跟踪问题应该保证(9)式成立:

(9)
定义输出跟踪误差积分项:

(10)
由(6)式和(8)式可得输出误差积分项为
υ(k+1)=v(k)+h(k)-θ(k)Cix(k).
(11)
为了提高故障检测系统和容错控制系统的性能,避免系统的重复设计。与以往分开设计故障检测系统和控制系统的方法不同,本文充分利用故障检测滤波器的信息,考虑输出跟踪精度,设计如(12)式所示的基于残差估计的输出跟踪容错控制器:
u(k)=K1i(k)+K2iυ(k),
(12)
式中:Ki=[K1iK2i]为待设计的容错控制器增益矩阵,K1i、K2i分别为待求的状态估计增益矩阵和输出跟踪增益矩阵。
基于以上分析,定义状态估计误差向量e(k)=x(k)-(k),故障估计误差向量re(k)=r(k)-f(k),系统增广状态向量xT(k)eT(k)vT(k)]T,增广干扰向量为ζ(k)=[ωT(k)fT(k)hT(k)]T,增广误差向量η(k)=[εT(k)]T,可得增广系统如(13)式所示:
(13)
式中:
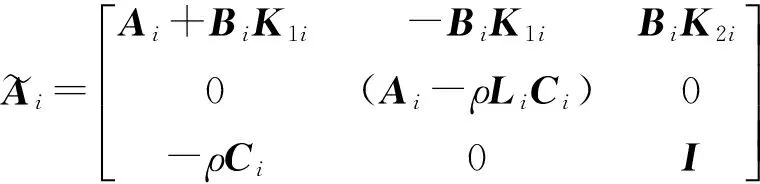

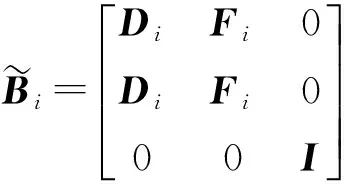

为了能够有效检测出故障,且保证系统具有一定的鲁棒性,将问题归结为寻找故障检测滤波器(7)式和输出容错控制器(12)式,使得增广系统(13)式全局一致渐近稳定且具有给定的H∞性能指标,即:
1)系统(13)式在ζ(k)=0时全局一致渐近稳定;
2)系统(13)式在零初始条件下满足:
(14)
式中:γ为鲁棒H∞性能指标。
为了实现故障检测,定义残差评估函数和阈值分别为
(15)
(16)
式中:l为故障检测时间窗口。
故障检测时间窗口l越大,则系统对外界干扰的鲁棒性越强,系统误报率越低。但是l的增大会引起系统计算量增大,导致故障检测速度下降。因此,为了获得满意的故障检测效果,应该合理设置窗口长度。
由于在飞行器内部普遍存在着时滞和丢包现象,会导致滤波器和控制器模态的切换滞后于系统模态的切换,产生异步切换现象。本文设定在切换时刻之后,系统能量函数增加,且增加率有界[15]。本文定义ki和ki+1代表子系统i激活和结束的时刻;T↑(ki,ki+1)和T↓(ki,ki+1)表示在区间[ki,ki+1)中系统Lyapunov函数增加或减小的区间。T↑(ki+1-ki)和T↓(ki+1-ki)分别表示Lyapunov函数增加和减小区间的长度。
综上所示,采用(17)式所示的逻辑进行故障检测:
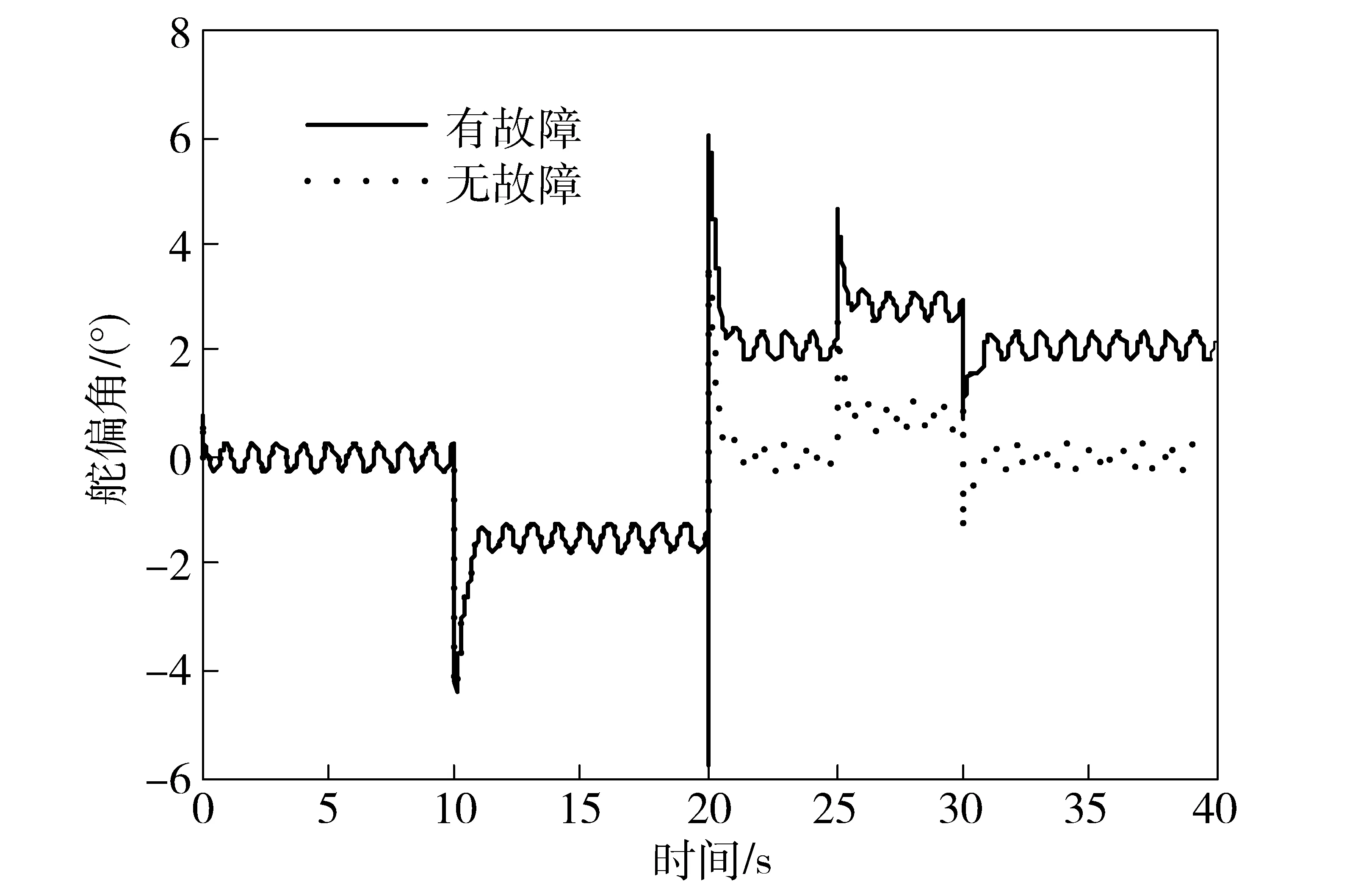
J(k)>Jth⟹故障,J(k) (17) 为了方便滤波器和控制器设计,引入以下定义和引理。 定义1[21]对于任意切换信号σ(k)和k2>k1>0,令Nσ(τ,k)表示切换信号在(k1,k2)内的切换次数,若存在N0≥0,τa>0使得 (18) 则称τa为平均驻留时间。 引理1[22]对于增广系统(13)式,如果给定常数0 κ1(‖x(k)‖)≤Vi(k)≤κ2(‖x(k)‖); (19) (20) Vi(k)≤μVj(k). (21) 如果切换信号的平均驻留时间满足: (22) 引理2[22]考虑增广系统(13)式,对于给定常数0 (23) 引理3 对于给定矩阵B∈Ru×n为列满秩矩阵,即rank(B)=n,则对B进行奇异值分解可以得到: 式中:U∈Ru×u、E∈Rn×n为两个正交矩阵,且满足U=[U1U2],U1∈Ru×n,U2∈Ru×(u-n);Σ=diag{λ1,…,λn},λ1,…,λn为矩阵B的n个非零奇异值。 若X∈Rn×n满足: X=ETΣ-1X1ΣE, (24) 式中:X1∈Rn×n>0,则存在非奇异矩阵∈Ru×u,使得B=BX,且 得证。 定理1 对于系统(13)式,给定常数0 Pi≤μPj,∀i、j∈Ω; (25) (26) (27) 证明 本文采用两步证明定理1: 1)首先证明在ζ(k)=0时,系统全局一致渐近稳定。 定义系统的能量函数: 当ζ(k)=0时,对于任意切换信号满足(22)式所示的平均驻留时间约束,有 由(26)式和Schur补定理可知 Δi(k)≤-ai(k),∀k∈T↓(ki,ki+1). 同理,由(27)式及Schur补定理可以证明: 综上所述,可以得到 因此,由引理1可知系统(13)式全局一致渐近稳定。 2)证明增广系统(13)式在零初始条件下的具有给定的H∞性能指标。 χ(k)TΞ1iχ(k)=χT(k)Γ1iχ(k). 由Schur补定理可知,(26)式等价于Γ1i<0,所以对∀k∈T↓(ki,ki+1): 由引理2可知:在零初始条件下系统(13)式全局一致渐近稳定,且具有(14)式所示的H∞性能指标,且γ=max{γi},i∈Ω. Pi<μPj,∀i、j∈Ω, (28) (29) (30) (31) (32) (33) 证明 设矩阵Bi可以进行奇异值分解为 式中:Ui、Ei为两个正交矩阵,且满足Ui=[U1iU2i];Σi=diag{λ1i,…,λmi},λ1i,…,λmi为矩阵Bi的m个非零奇异值。 可以得到: (34) (35) 式中: 由引理3可知,(34)式、(35)式等价于(29)式、(30)式,且控制器和滤波器参数可以由(31)式~(33)式求出。 故障检测滤波器的参数Wi可以直接通过解LMI(29)式、(30)式求出,此处不再赘述。 定理2 给出了故障检测器和容错控制器的求解方法,通过求解LMI,使得系统能够满足H∞性能指标,保证系统对外界干扰具有一定的鲁棒性。 本文以变体飞行器的纵向短周期运动为例进行仿真验证。考虑变体飞行器在高度H=12 000 m,Ma=0.5的状态下水平直飞,后掠翼在40 s内由15°变化到60°。选取ξ=15,20,25,…,60作为特征点进行切换子系统控制器和滤波器的设计。变体飞行器的纵向小扰动方程可以通过(1)式~(3)式进行计算,得到切换子系统模型。由于网络带宽的限制,系统中存在着丢包,本文假设丢包发生在传感器到控制器回路,丢包率ρ=0.9;由于信息传输时会引起时滞,本文考虑时滞为状态时滞,d=1. 由于篇幅限制,列出部分系统矩阵、状态时滞矩阵和输入矩阵分别为 式中:A15、Ad,15、B15、A60、Ad,60、B60分别表示机翼后掠角为15°和60°处的系统矩阵、状态时滞系统矩阵和输入矩阵。选取输出矩阵Ci=[10]. 选择干扰为风干扰[23],可以描述为 式中:s(k)的初值定义为[0.010]T。 选择故障信号为升降舵偏角的常值偏转,即 选取扰动和故障分布矩阵分别为 本文假设机翼后掠角的变化函数为 (36) 式中:ξ1=15°;ξ2=60°. 本文假设Tmax=40 s,则可得到变体飞行器机翼后掠角在[0,Tmax]内的变化曲线如图2所示。 图2 机翼后掠角变化曲线Fig.2 Changing curve of wing sweep angle K15=[-0.91010.769],K20=[-2.6835.313], 通过对飞行器进行仿真校验,可以得到结果如图3~图5所示。其中图3为残差信号和残差评估函数。通过(15)式可以得到系统故障检测的阈值Jth=0.018 2. 由(16)式可以得到系统在t=20.05 s检测出故障,即J(k)>Jth,因此系统的检测延迟为0.05 s. 因此,本文设计的故障检测滤波器在存在时延、丢包和外界干扰的情况下依然能够快速、有效检测出故障。 图3 残差信号和残差评估函数Fig.3 Residual signal and residual evaluation function 图4 攻角响应信号Fig.4 Response signals of attack angle 图5 舵偏角响应信号Fig.5 Response signals of elevator deflection 图4为攻角响应信号,从图4中可以看出:在存在风干扰等扰动因素的情况下,攻角响应信号能够较好地跟踪指令信号h(k),具有良好的动态性能,且在故障发生的情况下仍然能够保证对指令信号的跟踪。因此,本文设计的输出容错控制器具有较好的动态性能。 图5所示为舵偏角响应信号,舵偏角信号大小合适,处于物理可实现的范围内,且在存在干扰和故障情况下,变体飞行器没有发生舵面饱和现象。 为进一步验证方法的鲁棒性,考虑系统模型的气动力系数和气动力矩系数存在±15%极限偏差的情况对系统进行仿真。以正向偏差(+15%)为例,得到仿真结果如图6、图7所示,其中图6表示在极限偏差情况下系统的残差信号和残差评估函数,图7为极限偏差情况下的攻角响应信号。从图6、图7中可以看出:在极限偏差情况下系统性能会有所下降,但是故障检测器仍然能够快速、有效地检测出故障;系统的阈值为Jth=0.022 3,检测延迟为0.09 s. 在故障情况下系统仍然能够保证对攻角指令信号的有效跟踪。综上所述,本文设计的故障检测滤波器和容错控制器具有较好的鲁棒性。 图6 不确定情况下残差信号和残差评估函数Fig.6 Residual signal and residual evaluation function under the condition of uncertainty 图7 不确定情况下攻角响应信号Fig.7 Response signals of angle of attack under the condition of uncertainty 通过1 000次蒙特卡洛仿真,在随机偏差情况下验证系统的鲁棒性。可以得到:在随机偏差情况下,系统存在虚报8次,漏报5次,因此,故障检测滤波器虚报率为0.8%,漏报率为0.5%,检测正确率为98.7%. 综上所述,在存在时延、丢包和外界干扰的情况下,采用本文设计的方法,能够保证变体飞行器快速、有效检测出系统故障;在发生故障的情况下,仍能保证系统的稳定性和对指令信号的跟踪性能。在系统存在不确定性的情况下,仍具有较好的鲁棒性。 本文针对存在时延和丢包的变体飞行器故障检测与容错控制进行了研究,结论如下: 1)将变体飞行器建模为以高度、马赫数和后掠角为参变量的切换系统。 2)考虑系统中时延和丢包引起的异步切换现象,设计了故障检测滤波器和输出跟踪容错控制器。 3)通过Lyapunov-Krasovskii函数方法和平均驻留时间方法得到了保证系统全局一致渐近稳定并且具有一定H∞干扰抑制指标的充分条件。 References) [1] 何墉, 章卫国, 王敏文, 等. 基于多目标控制的变体飞行器切换线性变参数控制器[J]. 控制理论与应用, 2015, 32(11): 1519-1525. HE Yong, ZHANG Wei-guo, WANG Min-wen, et al. Switching linear-parameter-varying controller for morphing aircraft based on multi-objective[J]. Control Theory & Applications, 2015, 32(11):1519-1525. (in Chinese) [2] Jiang W L, Dong C Y, Wang Q. A systematic method of smooth switching LPV controllers design for a morphing aircraft[J]. Chinese Journal of Aeronautics, 2015, 28(6): 1640-1649. [3] Fiacchini M, Jungers M. Necessary and sufficient condition for stability of discrete-time linear switched systems: a set-theory approach[J]. Automatica, 2014, 50(1):75-83. [4] Yuan C Z, Wu F. Asynchronous switching output feedback control of discrete-switched linear systems [J]. International Journal of Control, 2015, 88(9):1766-1774. [5] 方志明, 向峥嵘. 一类切换系统切换序列的优化设计[J]. 兵工学报, 2011, 32(1):124-128. FANG Zhi-ming, XIANG Zheng-rong. Optimal switching sequence for a kind of switched systems[J]. Acta Armamentarii, 2011, 32(1):124-128. (in Chinese) [6] 陈章, 梁斌, 张涛, 等. 一种基于切换控制律的机器人双边遥操作方法[J]. 宇航学报, 2015, 36(4):410-418. CHEN Zhang, LIANG Bin, ZHANG Tao, et al. A switching control law based bilateral teleoperation approach for robot [J]. Journal of Astronautics, 2015, 36(4):410-418.(in Chinese) [7] 李杰, 齐晓慧, 夏元清, 等. 线性/非线性自抗扰切换控制方法研究[J]. 自动化学报, 2016, 42(2): 202-212. LI Jie, QI Xiao-hui, XIA Yuan-qing, et al. On linear/nonlinear active disturbance rejection switching control [J]. Acta Automatica Sinica, 2016, 42(2): 202-212. (in Chinese) [8] 王奇, 吴文海. 一种非线性自适应切换控制混合方法及其在倾转旋翼机上的应用[J]. 航空学报, 2015, 36(10): 3359-3369. WANG Qi, WU Wen-hai. A nonlinear adaptive switching control blending method and its application to tiltrotor[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3359-3369. (in Chinese) [9] 沈桂鹏, 王从庆, 王琪. 双框架飞机蒙皮检测机器人切换运动控制方法[J]. 航空学报, 2015, 36(6):2064-2073. SHEN Gui-peng, WANG Cong-qing, WANG Qi. Switching motion control of an aircraft skin detection robot with double frames[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6):2064-2073. (in Chinese) [10] de Souza C E , Coutinho D. Robust stability and control of uncertain linear discrete-time periodic systems with time delay[J]. Automatica, 2014, 50(2):431-441. [11] 詹习生, 吴杰, 关治洪, 等. 基于丢包和带宽限制网络化系统稳定性分析[J]. 控制理论与应用, 2014, 31(8): 1111-1115. ZHAN Xi-sheng, WU Jie, GUAN Zhi-hong, et al. Stability ana-lysis of networked system based on packet dropouts and bandwidth constraints[J]. Control Theory & Applications, 2014, 31(8): 1111-1115. (in Chinese) [12] 李岳炀, 钟麦英. 具有多测量数据包丢失的线性离散时变系统故障检测滤波器设计[J]. 自动化学报, 2015, 41(9): 1638-1648. LI Yue-yang, ZHONG Mai-ying. Fault detection filter design for linear discrete time-varying systems with multiple packet dropouts[J]. Acta Automatica Sinica, 2015, 41(9): 1638-1648. (in Chinese) [13] 彭建鑫, 刘海鸥, 王滨, 等. 自动变速操纵系统稳态过程故障检测和诊断技术研究[J]. 兵工学报, 2013, 34(11): 1352-1358. PENG Jian-xin, LIU Hai-ou, WANG Bin, et al. Research on fault detection and diagnosis of automatic transmission control system under steady state condition[J]. Acta Armamentrii, 2013, 34(11): 1352-1358. (in Chinese) [14] Chadli M, Abdo A, Ding S X.H_/H∞fault detection filter design for discrete-time Takagi-Sugeno fuzzy system[J]. Automatica, 2013, 49(7):1996-2005. [15] Du D S, Jiang B, Shi P. Fault detection for discrete-time switched systems with intermittent measurements[J]. International Journal of Control, 2012, 85(1): 78-87. [16] Feng J, Wang S Q, Zhao Q. Closed-loop design of fault detection for networked non-linear systems with mixed delays and packet losses[J]. IET Control Theory and Applications, 2013, 7(6): 858-868. [17] Wang Z L, Wang Q, Dong C Y, et al. Closed-loop fault detection for full-envelope flight vehicle with measurement delays[J]. Chinese Journal of Aeronautics, 2015, 28(3): 832-844. [18] Li J, Yang G H. Simultaneous fault detection and control for switched systems under asynchronous switching[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2013, 227(1): 70-84. [19] 周东华, 刘洋, 何潇. 闭环系统故障诊断技术综述[J]. 自动化学报, 2013, 39(11): 1933-1943. ZHOU Dong-hua, LIU Yang, HE Xiao. Review on fault diagnosis techniques for closed-loop systems[J]. Acta Automatica Sinica, 2013, 39(11): 1933-1943. (in Chinese) [20] Yang T T, Li A J, Niu E Z. Robust dynamic output feedback control for switched polytopic systems under asynchronous swit-ching[J]. Chinese Journal of Aeronautics, 2015, 28(4): 1226-1235. [21] Zhang L X, Shi P. Stability,l2-gain and asynchronousH∞control of discrete-time switched systems with average dwell time [J]. IEEE Transactions on Automatic Control, 2009, 54(9): 2193-2200. [22] Zhang L X, Gao H J. Asynchronously switched control of switched linear systems with average dwell time [J]. Automatica, 2010, 46(5): 953-958. [23] Guo L, Chen W H. Disturbance attenuation and rejection for systems with nonlinearity via DOBC approach[J]. International Journal of Robust and Nonlinear Control, 2005, 15(3): 109-125. Integrated Fault Detection and Fault Tolerant Control for Morphing Aircraft CHENG Hao-yu1, DONG Chao-yang1, JIANG Wei-lai2, WANG Qing3, SUI Han1 (1.School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China; 2.College of Electrical and Information Engineering, Hunan University, Changsha 410082, Hunan, China; 3.School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China) Considering the state delay and missing measurements in the network environment, the closed-loop fault detection for the morphing aircrafts with alterable sweep wings is investigated based on the switched system theory. The morphing aircraft is modeled as switched system which takes the altitude, Mach and wing sweep angle as parameters. Based on the integrated design method, the mode-dependent observer-based filter and the state estimation feedback controller are derived to ensure that the fault signal can be detected efficiently and the output can track the command signal accurately. The stability of the system is guaranteed by Lyapunov-Krasovskii functional method and average dwell time method. The sufficient existing conditions of filter and controller are given in the form of linear matrix inequalities (LMI). The simulated results show that the proposed method can detect the fault signal efficiently, the output can be used to track the command signal, and the system is robust to parameter uncertainties. ordnance science and technology; morphing aircraft; fault detection; fault tolerant control; asynchronous switching 2016-05-10 国家自然科学基金项目(61273083、61374012) 程昊宇(1990—), 男, 博士研究生。E-mail: chenghaoyu@buaa.edu.cn 董朝阳(1966—), 男, 教授, 博士生导师. E-mail: dongchaoyang@buaa.edu.cn V249.121 A 1000-1093(2017)04-0711-11 10.3969/j.issn.1000-1093.2017.04.0122 主要结论


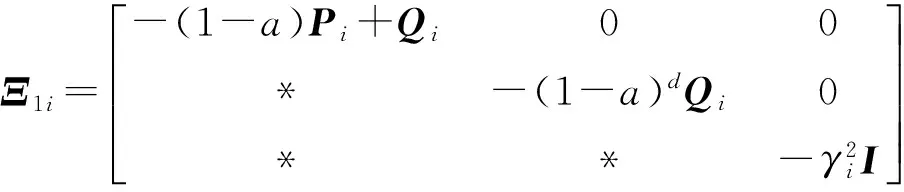







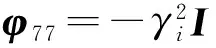



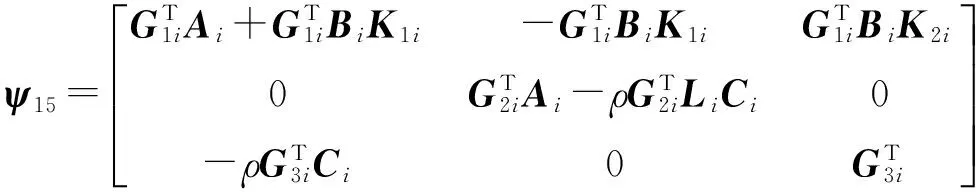

3 仿真校验



K25=[-2.8654.931],K30=[-2.9124.675],
K35=[-3.0054.423],K40=[-3.1214.328],
K45=[-3.2174.221],K50=[-3.3114.156],
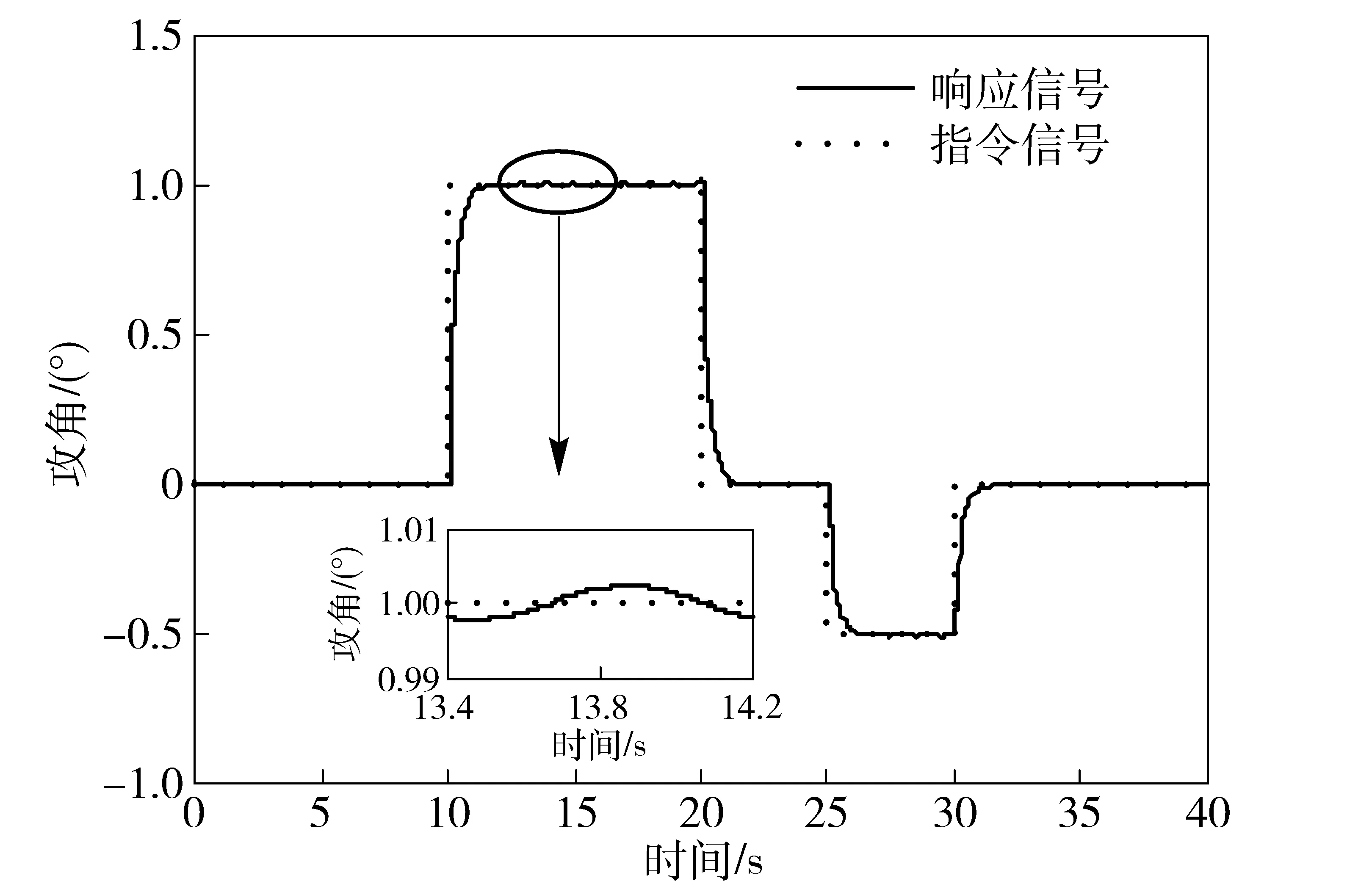


4 结论
