我国寿险资金的投资分析及其风险管理
2017-04-25陈佳豪林思亮杨德慧
陈佳豪 王 静 丁 璐 林思亮 杨德慧
(湖北经济学院,湖北 武汉 430205)
我国寿险资金的投资分析及其风险管理
陈佳豪 王 静 丁 璐 林思亮 杨德慧
(湖北经济学院,湖北 武汉 430205)
保险业作为现代服务业的重要板块,近年来在我国经济社会发展中已占有举足轻重的地位,其中寿险业作为保险业的一大分支,其经营的好坏直接影响保险业发展。随着保险市场竞争日益加剧,以及利率市场化的全面施行,如何进行寿险资金投资组合的选择和有效的风险管理,已成为我国寿险公司甚至是整个保险业发展过程中亟待解决的问题。本文从风险管理的角度来研究我国寿险资金最优投资结构,并根据结果提出建议。
风险管理;寿险资金;投资结构
一、引言
我国寿险业务规模自上世纪90年代开始进入快速扩张模式,1997年后,寿险保费规模更是以每年近40%的速度激增,直到2005年后增速才有所回落,截止2015年,我国寿险保费收入达到了1.6万亿,同比增长25%,寿险行业实际投资收益率为7.91%,五年平均收益约为5.32%。从单个公司来看,在投资收益率排行最高的是前海人寿,2015年实际收益高达21.87%,排行66的恒大人寿则为1.86%,虽整体都呈现出收益状态,但行业内部投资收益差距较大是不争的事实,且资产排行前十的人寿保险公司在投资收益率方面并不是十分靠前,以总资产24351亿元在资产榜排行首位的中国人寿的实际收益率仅为7.12%,排行38,五年平均收益率为4.91%,排行第35。之后的平安人寿、中国人保、新华人寿等资产规模靠前的公司在投资收益率方面也相对落后。我国寿险业保费增长速度过快与投资收益率之间存在一定的矛盾,说明其中必然存在一定的经营风险和偿付风险。因此,寿险公司应当更加重视寿险投资的业务风险,不断的优化寿险资金投资结构,通过提高投资收益率来应对公司经营风险。
二、寿险资金投资最优结构的构建
(一)风险度量模型的确定。
1.模型的选择。
从现代金融资产风险测量的发展情况来看,主要用到或用到过的方法有三种:一是VaR(Value-at-Risk),这种方法起源于上世纪80年代末,其核心思想在于将预期未来事件导致损失的大小和该事件发生的可能性综合计算,并在不同置信水平上求得VaR值,进而得出不同置信水平上的预期损失的大小,此方法有点在于金融机构能够应用此结果来对风险进行统一管理,缺点在于VaR值的假定条件是正常市场,没有将极端情况考虑到其中,并且对风险的度量不是一致性的;二是CVaR(Conditional Value-at-Risk),这一方法是在VaR的基础上发展而来,反映的是大于VaR的计算损失的平均值,即超额损失(VaR)的平均水平,是一个条件期望,优势在于能够将潜在风险价值较好的体现出来,数学理论性质较强,且用CVaR值代替方差与均值进行分析时,不同于用“均值—方差”模型中无法用方差表示投资组合的预期损失,“均值—CVaR”是能够将投资组合的预期损失表示出来的,且依然能够度量极端情况下的风险损失,即尾部风险损失。
基于此,本文选择以“均值—CVaR”风险度量模型为基础,来构建寿险资金的最优投资组合。
根据“均值—方差”模型(见式2-1)
式(2-1)
可以得出“均值—CVaR”风险度量模型如式(2-2)所示:
式(2-2)
2.寿险最优投资模型的假设条件。
根据“均值—CVaR”风险度量模型的适应条件以及资产组合理论、我国寿险行业及其他金融行业的实际情况和相关政策,对寿险最优投资模型的最终确定提出以下几点假设:
(1)寿险公司(即寿险资产管理者)对投资收益的期望是极大化的;
(2)寿险公司投资视野为单周期;
(3)寿险公司会综合期望收益率与风险损失率来寻求最优投资组合,即同风险前提下选择高收益组合,同收益前提下选择低风险投资组合;
(4)寿险行业乃至金融市场是有效市场;
(5)风险资产之间收益率存在一定关联;
(6)金融市场的样本数据的选择从长期角度来看应当服从正态分布;
(7)寿险资金投资不允许卖空,也就是说式(2-2)中xi≥0。
3.“均值—CVaR”风险度量模型的构建。
将寿险资金的资产组合应用到“均值—CVaR”风险度量模型中时,x=xT表示风险资产的种类,xi表示风险资产的权重,用r表示风险资产收益率,用uT表示期望收益向量,则有ui=E(ri),V=(σij)n×n则为风险资产的协方差矩阵,因此,有期望收益率为E(x)=xTu,方差则为σ2(x)=xTVx,在前一小节中,假设资产收益率服从正太分布,因此,可得投资损失计算公式为f(x,r)=-xTr~N(-E(x),σ2(x))。
再根据VaR模型定义,可以得出:VaRβ=Φ-1(β)σ(x)-E(X)
则有:
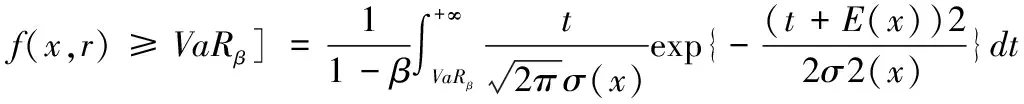
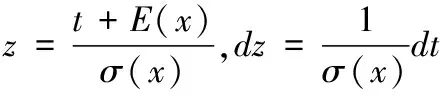
式(2-3)
而对于寿险资金的投资组合而言,其必然对稳健性和安全性有较高的要求,因此,其中必然包含一种无风险资产,此处用rf无风险资产的收益率,x0表示无风险资产的权重(即投资比例),则可得出寿险投资资产损失函数为:
f(x,r)=-xTr-x0rf
式(2-4)

式(2-5)
将以上计算结果代入式2-2后,可得寿险资金投资结构模型如式(2-6)所示:
式(2-6)
式(2-6)的目标函数为二次,线性约束。其中R0表示目标收益率,由各寿险公司根据公司的发展策略来确定,再将资产组合中各项资产的收益率、协方差等相关数据代入式(2-6)中,使用Matlab软件即可将各项资产的权重xi(即寿险资金投资资产的比例)和对应的CVaR值(平均超额损失)计算出来。
(二)寿险资金投资资产的确定。
1.资产组合的选择。
目前,我国寿险资金的投资资产组合比较多样,但主要仍以国债投资、企业债投资、基金投资、股票投资、银行存款为主,因此,本文在分析时,也以这五种金融资产的寿险投资资产组合的分析对象,其中,国债投资用中证国债指数代替,企业债投资用中证公司债指数代替,基金投资用中证基金指数代替,股票投资用沪深300指数代替,这一做法的目的在于把指数作为投资资产、工具或虚拟“股票”的市场价格来计算。
根据这五种资产的特性,本文将银行存款作为寿险投资组合中的无风险资产,其他四种资产则为风险资产。
2.资产收益率的确定。
为了保证本研究的科学性和时效性,对相关样本数据选择的期限为2011-2015年。
银行存款作为无风险投资资产,其资产收益率以银行活期存款月利率为准,查询相关数据可知银行存款收益率为0.382%。
在风险资产方面,使用国泰安数据库查询后可得,中国国债指数月收益率为0.363%,公司债指数月收益率为0.501%,中证基金指数月收益率为0.735%,沪深300指数月收益率为0.566%。而这四种指数月收益率的标准差如表2.1所示:
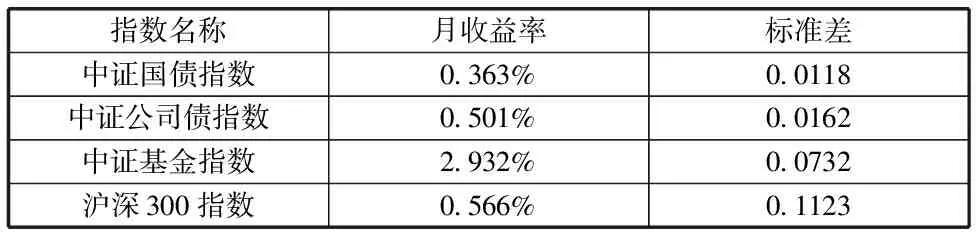
表2.1 风险资产投资收益及风险状况
从表2.1可以初步分析出,这四项资产的投资风险中,国债最低,公司债其次,基金再次,股票投资风险最高,这与我国金融市场情况基本相符。其中又以基金的月收益率最高,达到了3.245%,远高于2015年我国寿险行业平均投资收益率(平均月化收益率为0.659%)。
3.各项资产投资权重(比例)的限制。
根据我国保监会对保险行业的政策要求中可知,寿险公司各项资产投资权重(比例)的限制条件如表2.2所示:

表2.2 寿险公司投资资产权重(比例)限制条件
(三)最优投资组合模型求解
通常而言,寿险公司的超额损失CVaR要低于高风险限额,且确保CVaR高于最高风险限额的概率较低(此处取5%),因此,可以取置信水平β为95%,也就是寿险资金投资结构模型中为0.95,将以上投资收益率与相关数值代入寿险投资组合模型后,可得最终模型结果如式(2-7)所示:
式(2-7)
选取6个既定投资组合收益率R0,根据CVaR最小原则,得到个资产最优比例如表2.3所示:

表2.3 寿险资产组合最优比例(%)
从表2.3可以看出,寿险投资收益率越高,CVaR值也越大,与收益越高、风险越大的原则一致。而期望收益率的无论是在哪一种投资期望的情况下,股票的比例均为0,说明寿险资金尽可能不要持有股票资产,造成这种情况的原因在于股票与基金为限制条件互相冲突,而股票的收益率虽然较高,但风险明显要高于基金,收益与风险不呈正比,而基金的投资收益则要明显高于其他资产,但这明显与投资资产组合的稳定性和安全性相违背,说明我国股票市场还不够成熟,对寿险投资的安全性造成了一定的影响。
三、结论
通过对我国寿险资金投资资产组合最优结构的确定可知,我国整个金融市场还不够完善,特别是在股票市场方面,风险与收益存在较大的矛盾。而针对寿险资金不断累积的情况,为了进一步发挥寿险资本对社会经济的推动和保障作用,我国政府和相关机构应进一步推动金融市场规范化发展,同时,各寿险公司也应当不断提高自身投资管理水平,强化内部监管,进一步提高寿险资金的运作效率。
[1] 白雯娟,朱凯丽.我国寿险资金投资结构分析[J].海南金融,2014(12).
[2] 王波.多利率下寿险资金的最优投资计划与费率计算[J].保险职业学院学报,2015(02).
[3] 靳珂.我国保险投资组合风险管理:基于VaR的研究[J].河南社会科学,2016(02).
[4] 鲍静海,王楹,徐丽琳.我国寿险公司资金运用效率的实证分析——基于三阶段DEA模型[J].金融理论与实践,2016(02).
