AIT阵列感应测井在鄂尔多斯盆地致密油储层的侵入校正

2017-04-24夏宏泉吕斯端文晓峰

测井技术 2017年6期

夏宏泉, 吕斯端, 文晓峰

(1.油气藏地质及开发工程国家重点实验室西南石油大学, 四川成都 610500; 2.中国石油集团测井有限公司长庆事业部, 陕西西安 710200)

0 引言

鄂尔多斯盆地陇东地区延长组致密油储层泥浆侵入严重,使得测井视电阻率偏离地层真电阻率,必须对泥浆侵入的影响进行校正[1]。本文以斯伦贝谢公司AIT阵列感应测井电阻率曲线校正为例进行研究分析。阵列感应测井常规迭代反演法要达到某一精度所需的迭代次数可能很多,降低了数据处理效率[2-3]。本文提出了一种快速的阵列感应测井电阻率校正方法。首先分析泥浆侵入对阵列感应测井电阻率测井响应的影响机理,然后对阵列感应测井视电阻率进行泥浆侵入校正以求得地层真电阻率,推导校正公式模型,并利用校正后的深电阻率曲线计算地层含水饱和度,与实测含水饱和度进行对比,以检验其校正的合理性,同时计算出泥浆侵入深度,为后续射孔作业提供射孔深度依据。

1 工区测井概况及AIT响应特征分析

1.1 测井概况

鄂尔多斯盆地陇东地区延长组地层标准段为低孔隙度低渗透率致密油储层,测井装备一般需采用高精度的EILog、PEX、LOGIQ、ECLIPS-5700、MAXIS-500等系列[4]。该区致密油储层的测井评价面临3大难题。①有效储层划分困难:陇东地区延长组储层岩性和孔隙结构复杂,储层与非储层间的测井响应差异小、特征不明显,有效储层划分困难。②油水层识别困难:该区延长组油水分异不明显,油水同层现象普遍,束缚水饱和度高,并且钻井液深侵入改变了井筒附近的流体性质,造成油层与水层的测井响应特征差异小、对比度低,对油水层的识别带来困难。③储层参数计算精度低:该区延长组储层的非均质性导致测井响应复杂,非阿尔奇现象普遍,传统的均值测井响应体积模型适应性差,储层参数定量解释精度低。

1.2 AIT响应特征分析

AIT阵列感应测井具有分辨率高、探测深度大、直观显示泥浆侵入等特点[5-6],各测井曲线探测深度如表1所示。

表1 AIT电阻率测井探测深度

陇东地区钻井一般采用淡水泥浆,而地层水矿化度高,所以,油层电导率<泥浆电导率<水层电导率。根据电阻并联原理可知,油层的深阵列感应测井视电阻率AT90小于Rt,而水层的深阵列感应测井视电阻率AT90大于Rt。油层深阵列感应测井视电阻率未作泥浆侵入校正将导致计算出的含水饱和度偏大;水层深阵列感应测井视电阻率未作泥浆侵入校正将导致计算出的含水饱和度偏小。

2 阵列感应测井的泥浆侵入影响校正

2.1 泥浆径向侵入地层分带模型

阵列感应测井仪器纵向分辨率约为0.6 m,当层厚低于0.6 m时,识别薄油气层误差较大。另外,工区中大部分井段并未出现严重扩径的情况,因此,可以忽略井眼扩径对浅探测电阻率曲线的影响。

为更加直观地还原泥浆侵入过程,可将阵列感应测井径向探测地层分为井筒泥浆、冲洗带、侵入带和原状地层4个部分。

阵列感应测井测量的地层视电导率为[7]

(1)

式中,σa为地层视电导率,S/m;gr,z为阵列感应测井微分几何因子,S/m;σr,z为地层微分电导率,S/m;r为径向深度,m;z为纵向高度,m。

在各部分电导率相对稳定的情况下,那么阵列感应测井测量的地层视电导率满足式(2)

(2)

式中:σm为泥浆电导率,S/m;σxo为冲洗带地层电导率,S/m;σi为侵入带地层电导率,S/m;σt为原状地层电导率,S/m;r0为井筒半径,m;r1为冲洗带半径,m;r2为侵入带半径,m。

Gxo+Gi+Gt=1

(3)

2.2 校正方法推导

由式(2)和式(3)可以看出,不同探测深度的阵列感应测井电导率通过σxo、σi、σt加权得到,但是几何因子并不相同,可以得到冲洗带、侵入带及原状地层视电导率表达式为

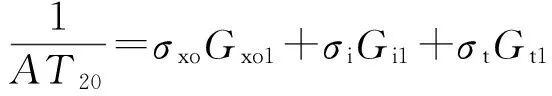
(4)

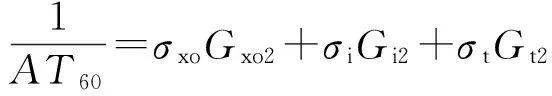
(5)

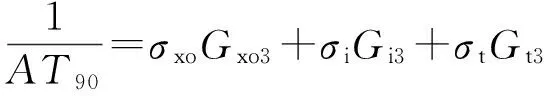
(6)

式中,AT20、AT60和AT90分别为浅、中、深阵列感应测井视电阻率。欲通过式(4)～式(6)解出σxo、σi和σt,必须要知道不同探测深度条件下的阵列感应测井几何因子,即需要求得阵列感应测井径向微分几何因子。gr与阵列感应测井仪器参数关系密切,计算方法[9-10]为

(7)

(8)

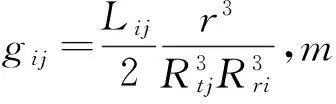
将几何因子G沿径向积分,可以得到不同探测深度条件下的地层电导率径向积分几何因子(见图1)。

图1 不同探测深度地层电导率积分几何因子

由图1可以得到,AT20、AT60和AT90相对应的地层电导率几何因子Gxo、Gi和Gt(见表2)。

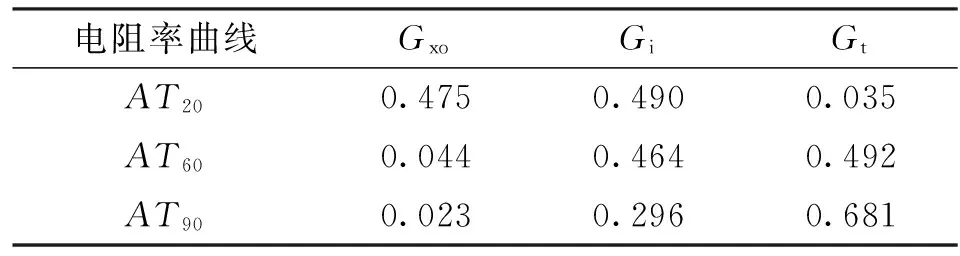
表2 不同探测深度的地层电导率几何因子

代入数据,联立式(4)、式(5)和式(6)可得

(9)

(10)

利用Rt=1/σt、Rxo=1/σxo即可求解地层真电阻率和冲洗带电阻率。

根据阵列感应测井仪器的径向几何因子理论,可以推导出计算泥浆侵入带直径Di的公式[11]为

(11)

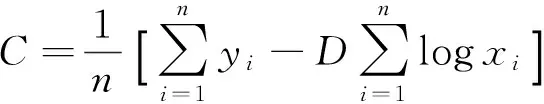
(12)

(13)

式中,σm为泥浆电导率,S/m;n为径向分辨率(探测深度)种类数,AIT阵列感应测井仪器n取5;xi为仪器径向探测深度,分别取10、20、30、60和90 in*非法定计量单位,1 ft=12 in=0.304 8 m,下同,在求系数C、D时,yi应取20、60或者90 in径向探测深度所对应的径向积分几何因子。将式(9)、式(10)、式(12)和式(13)代入式(11)即可求出泥浆侵入深度。

表3为该方法计算的Rt和Di值与斯伦贝谢公司双感应-八侧向组合测井的泥浆侵入影响校正图版读出的Rt和Di的相对误差统计。

从表3可以看出,深度为1 987.5 m和1 989.5 m时,AT20/AT90值和AT60/AT90值差距很小,用阵列感应测井几何因子法计算的泥浆侵入深度与图版读值误差很大,说明AT20、AT60、AT90差异不大时此方法计算侵入深度效果不好。因此,当AT20、AT60、AT90差异明显时,阵列感应测井几何因子法与传统校正图版法来获取地层真电阻率和侵入深度,两者的结果比较接近,能达到地质和工程应用的精度要求。

表3 Y井计算的Rt和Di与传统校正图版读出的Rt和Di的相对误差表

3 应用实例分析

鄂尔多斯盆地致密油储层泥浆侵入严重,具体表现在油层出现泥浆低侵入特征,阵列感应测井曲线AT10、AT20具有幅度差,而AT30、AT60、AT90基本上重合,表明泥浆侵入深度至少达到了20 in,图2为Z258井1 835～1 875 m井段阵列感应测井电阻率曲线泥浆侵入校正前的解释结论。水层AIT曲线特征差异较明显,出现泥浆高侵入特征,阵列感应测井曲线AT10、AT20、AT30具有幅度差,而AT60、AT90基本上重合,表明泥浆侵入深度至少达到了30 in。

基于上述方法,编制处理程序校正了工区多口井的阵列感应测井电阻率曲线,输出了校正后地层真电阻率曲线Rt、校正后的含水饱和度曲线Swc及泥浆侵入深度Di曲线。校正后的电阻率所计算的含水饱和度与密闭取心实测含水饱和度的对比见表4。

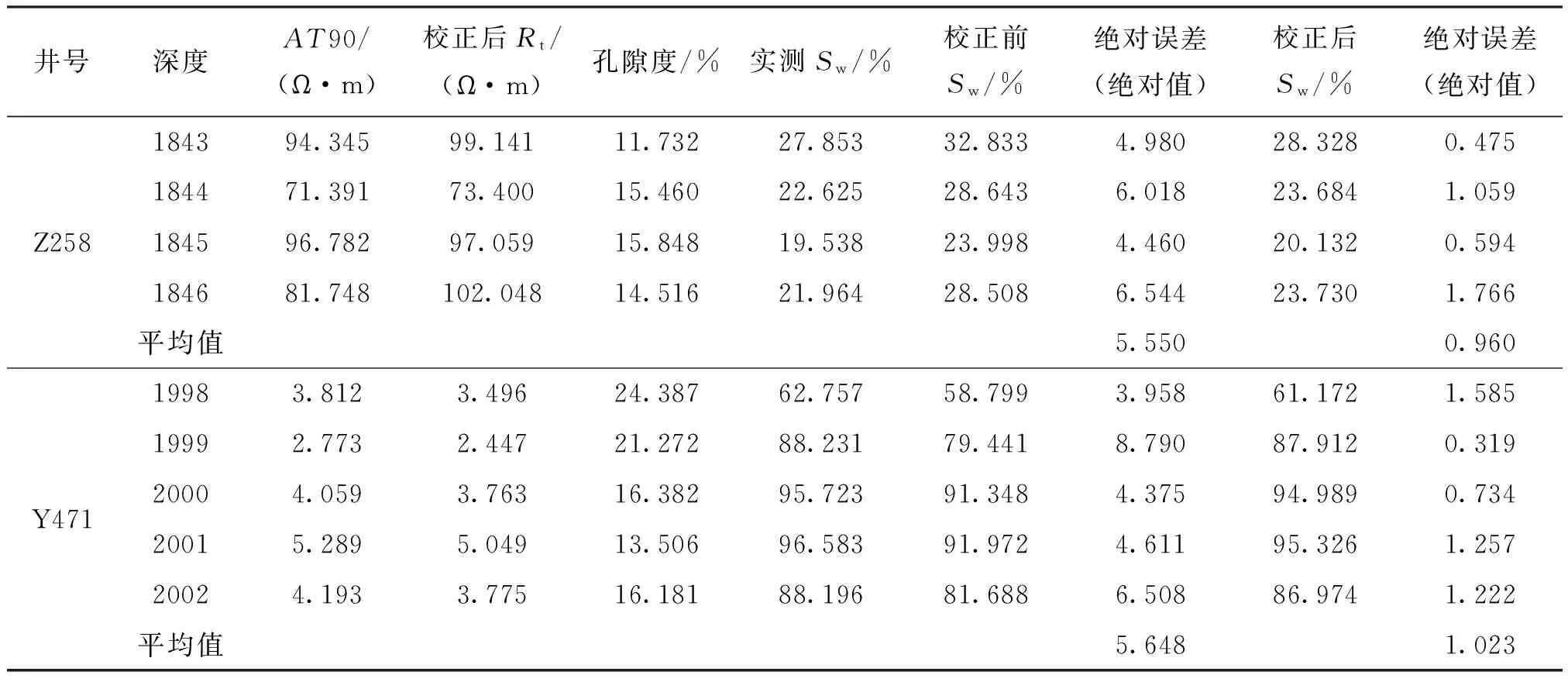
表4 2口井校正前后含水饱和度与实测含水饱和度误差

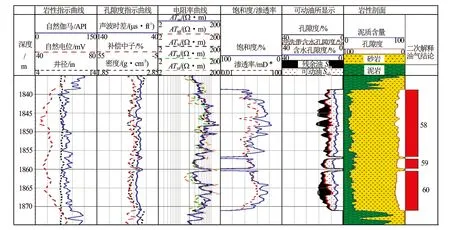
图2 Z258井1 835～1 875 m段泥浆侵入校正前解释成果图

图3 Z258井1 835～1 875 m段油层阵列感应测井电阻率曲线泥浆侵入校正后的成果图*非法定计量单位,1 mD=9.87×10-4 μm2,下同

图3为Z258井1 835～1 875 m井段阵列感应测井电阻率曲线校正成果图。其长8段1 838.8～1 856.6 m是岩性为粉-细砂岩的油层,储层物性好,泥浆低侵明显,校正后地层真电阻率相比校正前平均增大24.5%,含水饱和度相对校正前平均降低6.2%,符合油层电性特征,且计算出泥浆侵入最大深度为44 in,可以为射孔枪弹的选取提供依据。