框架剪力墙结构侧向加载模式下的Pushover分析
2017-04-21王星星廖光明施秀虎缑文平
王星星 廖光明 施秀虎 缑文平
(1.贵州省建筑设计研究院,贵州 贵阳 550002; 2.四川大学建筑与环境学院,四川 成都 610065)
框架剪力墙结构侧向加载模式下的Pushover分析
王星星1廖光明2施秀虎1缑文平1
(1.贵州省建筑设计研究院,贵州 贵阳 550002; 2.四川大学建筑与环境学院,四川 成都 610065)
介绍了Pushover分析的基本方法,阐述了几种典型的水平侧向力分布的原理特征及选取原则,并结合某超高层框架剪力墙工程实例,分析了不同加载模式下结构薄弱部位发展、层间位移角大小、性能点的出现等情况,最后提出了薄弱构件的加强措施。
Pushover分析,侧向力分布,塑性铰,层间位移角,抗震设计
近年来,震级较大的地震在我国频繁发生,如汶川地震、玉树地震、雅安地震等,使得大量的房屋建筑倒塌,给人民的生命造成严重地威胁,财产带来巨大的损失。为减少地震灾害的伤亡损失,工程设计人员应从防止结构在强震作用下的坍塌着手,逐步探明结构进入弹塑性阶段构件的内力、变形、薄弱构件的位置及塑性铰的发展情况着手,从而采取加强构造、加固薄弱构件等相应地措施实现“大震不倒”的性能目标。结构的静力弹塑性Pushover分析作为基于性能设计的一个重要分析方法,已倍受结构工程师所青睐,并广泛用于各种复杂、高大建筑结构的抗震分析中。
静力弹塑性Pushover分析方法结合了反应谱分析的特点在沿结构的高度方向施加规定形式的侧向水平力,并单调递增,直至结构构件由弹性、开裂、屈服、破坏或结构达到目标位移而停止分析[1]。侧向水平加载模式取决于实际地震中结构水平地震剪力,不同的推覆力得到的Pushover分析结果不一样。因此,侧向加载力的选取对高层建筑结构的Pushover分析结果至关重要。于是,有许多学者对Pushover分析中侧向力分布展开全面地研究;叶献国[2-4]对侧向力分布进行了改进和简化并提出循环往复加载模式;侯爽,欧进萍[5]进一步阐述了静力弹塑性分析的侧向分布及高阶振型的影响;杨红[6]研究了侧向力分布对结构抗震性能的控制。高层框架剪力墙结构的侧向力分布模式还有待进一步研究。
本文从几种侧向力分布出发,分析了一栋超高层结构在各种水平推覆力下的抗震性能,对比分析了结构塑性铰发展及薄弱构件的破坏,为工程实践提供依据。
1 Pushover分析的基本方法
Pushover分析方法克服了反应谱中不能分析结构在强震下进入弹塑性阶段的受力状况的缺点,同时又与时程分析中繁杂地计算量相比Pushover分析具有更简洁的计算工作且能够比较精确地反映强震激励下结构的承载力、内力、变形性能、能耗关系以及梁、柱、墙中塑性铰出现的顺序、位置等特征把握薄弱构件的破坏机理。
静力弹塑性分析的基本方法是:
1)根据Pushover分析建立结构的基底剪力—顶点位移关系(V—D)曲线。
2)能力谱曲线确定,将(V—D)曲线按式(1),式(2)转化为谱加速度—谱位移(Sa—Sd)曲线。

(1)
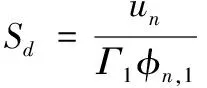
(2)
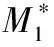
3)确定需求谱曲线,由(Sa—Sd)曲线再按式(3)进一步转化为结构的(ADRS)格式的需求谱曲线。
(3)
其中,un为结构顶底位移;φn,1为第n振型1质点的振幅。
4)性能点的确定,将上面得到的能力谱曲线和需求谱曲线绘制在同一坐标轴上两曲线的交点(如图1所示)即为结构的目标性能点。
2 水平侧力分布的介绍
结构在地震作用下由线弹性发展到弹塑性阶段,其侧向力的分布规律不仅受到来自地震动的周期、频谱、振幅和结构自振周期、振型分布函数等因素的影响,而且还受结构自身进入塑性状态内力重分布的制约,使得水平侧力加载模式变得十分复杂。已有学者对不同的侧向加载模式进行研究,并对加载模式的适用范围给出了一些建议。
2.1 水平侧力的分布形式
Pushover分析中所选取的水平侧向加载模式应能近似反映结构在地震中所受实际地震剪力产生的位移变形。常见的水平侧力的分布形式为美国规范FEMA-273[7]推荐的均匀分布加载、倒三角形分布及反应谱振型组合下的SRSS加载模式。随着研究的不断深入,又相继提出了抛物线加载模式、考虑高阶振型影响的加载、随振型变化的加载、等价基本质量的加载及自适应模式的加载方式。
2.1.1 均匀分布
该加载模式近似认为结构各楼层随地震加速度的大小相等,各层侧向力与其对应的楼层质量成正比,若各层的质量相等,则有侧向力Fi:
(4)
其中,Gi为第i层重力荷载代表值;VD为结构的基底总剪力;n为结构总层数。
2.1.2 考虑高度影响的分布
这种加载方法考虑了高度对结构侧向力分布的影响,则有Fi:
(5)
其中,Hi,Hj分别为第i,j层到基底的距离;k为楼层的高度修正指数。当主振型周期T≤0.5 s,k=1.0即为倒三角形加载模式,它是基于各楼层地震作用下的加速度一致的假定,结构的侧向力沿高度呈线性分布与我国建筑抗震规范[8]中给出的底部剪力法相似;T≥2.5 s,k=2.0;T为其他k线性内插。
2.1.3 SRSS分布模式
反应谱的振型组合加载模式根据文献[5]中振型分解得到地震力Fji,再进行平方和的平方根(SRSS)计算出各楼层的层间剪力并反算得到楼层的水平荷载,即为下一步Pushover分析的推覆荷载。

(6)

(7)
其中,αj,γj分别为第j振型的地震影响系数和参与系数;Xji,Qji分别为第i质点j振型的相对位移、楼层剪力;QVi,QVi+1分别为n个振型SRSS组合下第i,i+1层的地震剪力。
2.2 侧向力选取的注意事项
静力弹塑性Pushover分析中,当采用倒三角形分布的推覆力时应注意结构第一振型参与质量需大于总质量的75%,且需同时采用均布加载模式对比分析。若选取SRSS侧力模式,反应谱的振型参与系数应大于0.9,选取合理的地震动反应谱且第一主振型周期T≥1.0 s。
侧向力加载模式的选取还应把握结构可能出现的薄弱构件从而预测结构的破坏形式,便于准确选取接近实际地震破坏的侧向加载模式合理地对结构进行抗震性能评估。
3 框架剪力墙算例
3.1 工程概况
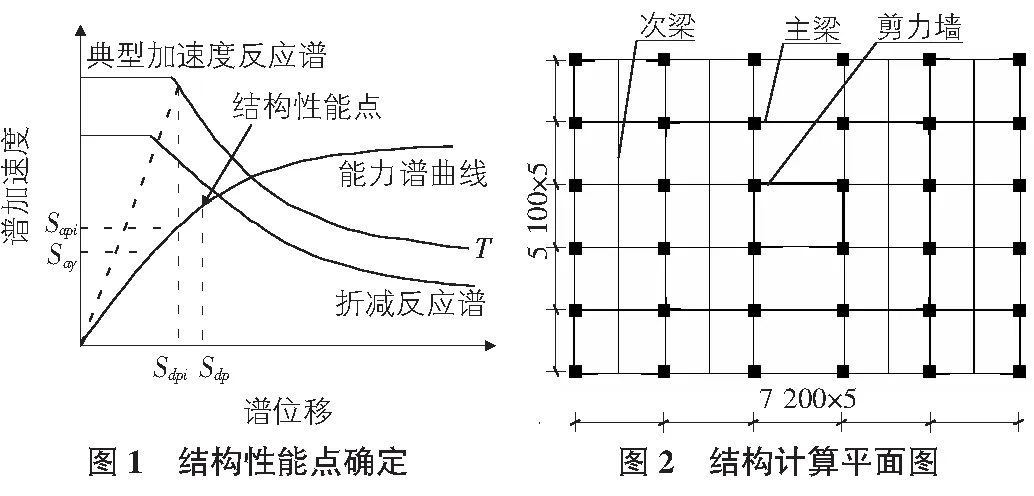
本文分析中的框架剪力墙结构为广州市某商业大厦,其平面尺寸如图2所示,地下1层层高为4.0 m,地上部分30层各层高3.6 m,结构总高度为108.4 m。抗震设防烈度为7度0.15g,场地类别为Ⅱ类第二组。梁间恒载为10.0,考虑楼板自重荷载后楼面恒载为3.0,活载为2.0,屋面恒载8.0,活载0.5。该框架剪力墙结构采用PKPM分析时满足现行抗震规范设计要求。构件的截面信息及材料强度信息见表1。

表1 构件及材料强度信息
本文采用的分析程序为Midas Gen,结构中梁配筋按1%的经济配筋率配筋,柱按2%经济配筋。墙厚300 mm的剪力墙垂直方向配筋为φ16@200,水平方向配筋φ12@200;墙厚250 mm的剪力墙其垂直方向配筋为φ14@200,水平方向配筋为φ10@200。该结构各构件截面、配筋信息均符合建筑抗震规范。Pushover分析中塑性铰定义采用FEMA273铰属性即框架梁I和J端为M3铰,柱子I和J端定义P-M-M相关铰;为保证剪力墙的延性避免发生剪切破坏,除在剪力墙的I, J端指定PM铰外还需在墙的中部定义剪力铰。
3.2 反应谱分析
对结构进行多遇地震下的弹性分析,得到X,Y方向的侧移值及层间位移角如图3,图4所示。


结构在X方向的最大侧移为89.56 mm,最大层间位移角在第19层处为1/970;Y方向的最大侧移为104.06 mm,最大层间位移角在第16层处为1/836,两个方向的层间位移角略低于规范限值的1/800,满足设计要求。X,Y方向的最大基底剪力及倾覆弯矩见表2。

表2 基底剪力和倾覆弯矩
3.3 Pushover分析
结构进行静力弹塑性Pushover分析时初始荷载为重力荷载代表值即:1.0恒载+0.5活载。X,Y方向的侧向水平加载力为常加速度(均布)加载、模态(倒三角形)加载及考虑多阶振型效应影响的SRSS组合三种侧向加载模式。
3.3.1 塑性铰的分布
图5分别给出了框架—剪力墙结构在三种加载模式下塑性铰的发展及分布情况。由图5a)可以看出三种侧向加载模式在X方向的塑性铰的分布差异较大,在均布力下结构的-1层~10层剪力墙的塑性铰颜色较深,构件发生严重地开裂直至倒塌破坏;而倒三角加载中第11层~15层的变形相对集中为薄弱层,其中部分连梁也发生失效。在SRSS分布力作用下结构的塑性变形性能较为稳定仅有少量的连梁构件发生破坏。图5b)中Y方向的三种加载模式的塑性铰发展情况近似都表现在第10层以上的部分剪力墙塑性变形较大破损严重。主要差别在均布加载模式下第-1层~5层剪力墙铰的发展与其他两种侧力模式下有所不同。薄弱构件应加强构造等措施进行加固。

3.3.2 抗震性能分析
如图6所示分别给出了Pushover分析下各加载工况结构的基底剪力—控制位移的关系曲线。可以看出均布加载得到的X,Y方向的基底剪力较大;倒三角形与SRSS工况下的基底剪力与控制位移的关系曲线比较接近。加载的前期结构在三种侧向力模式下的基底剪力与控制位移呈线性递增;结构处于弹性阶段;随着推覆力的不断加大结构体系进入弹塑性变形阶段,各侧向分布力下结构的基底剪力与控制位移开始表现出各自的差异性;其中均布加载力下差异性更为显著。
结构进行罕遇地震下的Pushover分析,得到性能点Sa,Sd值,再根据式(1),式(2)之间的关系求得结构性能点处的基底剪力V与顶点位移μn。图7分别给出了不同的加载模式下结构的顶点位移的曲线关系。结构在倒三角形和SRSS侧向力分布模式下的顶点位移比较接近约为550 mm,均布分布力作用得到的顶点位移显著低于其他两种分布形式的顶点位移。在罕遇地震下结构的弹塑性变形约为多遇地震中弹性侧移变形的5倍;强震作用下结构的延性性能比较高。
Pushover分析得到三种侧向力加载模式下结构X,Y方向的弹塑性层间位移角的关系曲线如图8所示。从图8可以看出结构各层的变形均匀,仅在第18层~21层发生较小范围的波动,结构整体变形以弯曲变形为主。不同的加载模式得到的层间位移角各具特性,其中在SRSS侧向加载模式下得到结构X,Y方向的层间位移角均为最大分别为1/152,1/135,低于规范限值的1/100,说明结构设计合理,在强震下具有较高地抗震性能。
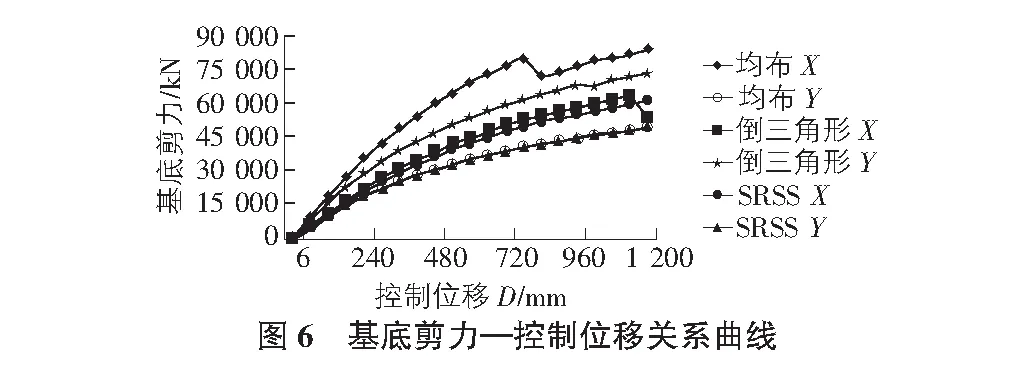
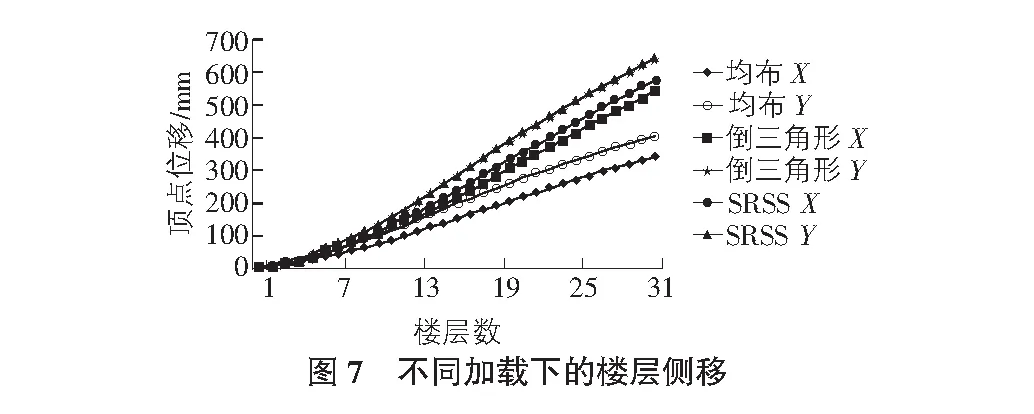

表3给出了各侧向力分布模式下结构X,Y方向的基底剪力与倾覆弯矩值。不同分析工况下结构性能点处的基底剪力近似一致,约为40 000 kN。

表3 基底剪力及倾覆弯矩
结构中的剪力墙抗侧刚度大,强震中承担了大部分的地震剪力。对比反应谱分析发现,结构进入弹塑性阶段的基底剪力、倾覆弯矩值大概是弹性阶段的3倍~4倍。因此,结构必须具有足够的刚度、强度以避免大震下的倒塌破坏。
4 结语
本文通过对一幢超高层框架剪力墙结构进行X,Y方向的均布、倒三角形及多振型下的SRSS组合的侧向加载模式下的Pushover分析并与弹性反应谱分析对比得出以下结论:
1)结构由多遇地震下的弹性变形发展到罕遇地震中的弹塑性阶段,其楼层侧移及层间位移角均满足抗震设计规范的要求,结构设计合理。
2)考虑高阶振型的影响,均布加载模式不能准确反映实际结构地震中受力状态;故可将均布加载的分析结果作为弹塑性设计的参考依据,对薄弱构件进行适当地加固处理。
3)建议根据倒三角形及SRSS两种侧向加载模式的分析结论
对结构第15层~20层的剪力墙及第15层以上的部分连梁等塑性铰发展较深的薄弱部位采取加强构造、结构加固等措施进行处理。
[1] 孙爱伏,欧进萍.高层钢结构抗震pushover分析的侧向力分布模式及其影响[J].地震工程与工程振动,2008,28(4):88-90.
[2] 叶献国.多层建筑结构抗震性能的近似评估——改进的能力谱方法[J].工程抗震,1998,12(4):10-14.
[3] 叶献国,周锡元.建筑结构地震反应简化分析方法的进一步改进[J].合肥工业大学学报,2000,23(2):149-153.
[4] 叶献国,种 迅,李康宁,等.Pushover方法与循环往复加载分析的研究[J].合肥工业大学学报,2001,24(6):1019-1024.
[5] 侯 爽,欧进萍.结构Pushover分析的侧向力分布及高阶振型影响[J].地震工程与工程振动,2004,24(3):89-97.
[6] 杨 红,骆文进,王志军,等.Pushover侧向力模式对框架地震反应的控制能力[J].浙江大学学报,2008,48(9):1526-1531.
[7] FEMA-273,NEHRP Guide-lines for the Seismic Rehabilitation of Building, FEMA, Washing-ton, D.C,1997.
[8] GB 50011—2010,建筑抗震设计规范[S].
Pushover analysis for frame shear wall structure under lateral loading modes
Wang Xingxing1Liao Guangming2Shi Xiuhu1Gou Wenping1
(1.GuizhouInstituteofArchitecturalDesign,Guiyang550002,China;2.SchoolofArchitectureandEnvironment,SichuanUniversity,Chengdu610065,China)
This paper describes the basic methods of Pushover analysis focuses on the principles of the principle characteristics of several typical horizontal lateral force distribution and selection, analysis the weak parts of the structure under different loading patterns of development, the size of inter-story drift occurs performance points and so on. Finally the weak members proposed targeted measures to strengthen.
Pushover analysis, lateral force distribution, plastic hinge, angle of displacement between layers, seismic design
1009-6825(2017)05-0055-04
2016-12-03
王星星(1986- ),男,硕士,工程师
TU398
A
