边界层自保持对建筑风压的影响研究

秦 刚 程 旭

(西南交通大学，四川 成都 610031)

边界层自保持对建筑风压的影响研究

秦 刚 程 旭

(西南交通大学，四川 成都 610031)

采用了一种大气边界层自保持的方法，并基于SST k-ω湍流模型，从压力等值线、平均风速和湍动能等方面，对建筑物表面风压进行了研究，指出大气边界层自保持方法可以应用于建筑物风压计算中。

计算风工程，SST k-ω湍流模型，表面风压，压力等值线

0 引言

随着电子计算机技术的迅速发展，数值模拟方法成为了一种越来越受到重视的风工程研究方法。数值模拟方法又称计算风工程(Computational Wind Engineering，或CWE)，计算风工程的核心内容为计算流体动力学(Computational Fluid Dynamics，或CFD)。与风洞试验和现场实测相比，CFD方法具有成本低、计算周期短、能够描述流场细节并给出计算流场的定量结果等优点。

结构风工程主要研究的对象都位于大气边界层内，边界层内的自然风有特有的统计特性。由于大气流动是不可压缩粘性流体的湍流运动，因此想要精确得预测结构风荷载，大气的湍流流动必须要做到模拟准确。大气边界层自保持相比于一般入口是在模拟大气边界层时，能够保证来流风平均剖面和湍动能剖面在建筑物上游的计算区域内保持不变。

现阶段研究中，较成熟并且应用较广的大多是基于标准k-ε湍流模型。但是已有研究表明[1]，在具有逆压梯度流动或者分离流动的数值模拟中，标准k-ε湍流模型并不能很好的适用。为了解决标准k-ε湍流模型对存在逆压梯度的流动及流动滞止区的处理不当的问题，Menter[2]提出的SST k-ω 模型被视为目前雷诺平均(RANS)方法中最适于钝体分离流模拟的两方程湍流模型，所以在数值模拟建筑风压中，一般都采用此湍流模型。

曾锴等[3]基于SST k-ω 湍流模型，研究了空数值风洞入口边界条件的保持问题。并分别给出了我国建筑工程中的 A，B，C，D 四类地表对应的入口湍流边界条件表达式，为实际工程应用提供了便利。虽然模拟的平均风剖面得到了较好保持，但是并未研究自保持的风场是否适用于有障碍物的情况。

唐煜等[4]基于SST k-ω湍流模型和平衡大气边界层假设，推导了对数型风剖面入口来流边界条件表达式，并给出了适用于较大地形尺度风场计算时湍流模型采用的常数建议值，推导了定常条件下入口边界的近似解，得到了大气边界层的较好保持。但是依然是在平坦地形和尺度非常大的山地计算域中计算。

综上所述，近些年来学者们对大气边界层自保持越来越重视，对于如何保持大气边界层的平衡也提出了各种方法。但是这些方法基本上都是在空计算域当中进行计算，并未应用到实际当中去。在建筑结构这类钝体结构绕流中，大气边界层虽然能够到达建筑结构前自保持，但是在绕结构分离之后，流场产生复杂变化。所以对大气边界层自保持方法是否能够应用到建筑结构模拟的验证，十分有必要。

1 控制方程与k-ω湍流模型

1.1 控制方程

任何运动都要符合一定的物理定律，微观的流体也不能例外。在计算风工程中，位于大气边界层内的气体流动属于低速运动，一般情况下我们并不考虑温度变化带来的影响，所以大气密度ρ一般当作常数来处理。大气边界层内的钝体绕流一般当成粘性不可压流体来计算，对应的控制方程包括质量守恒方程以及动量守恒方程。

不可压流的质量守恒一般描述为，对位于流体中的体积元，单位时间内净流出质量应等于净流入质量，该定律用连续方程可以表示为:

(1)

连续介质运动也需要满足牛顿第二定律。对于不可压缩流体中的一个体积元，体积元的加速度等于作用在其上的单位质量流体的表面力和质量力的合力之和，该动量守恒方程可以表示为:

(2)

该动量方程一般也被称作为Navier-Stokes方程(N-S方程)。

1.2 SST k-ω湍流模型

Menter[2]提出了剪切应力输送(Shear-Stress Transport)模型，简称SST k-ω湍流模型。该模型综合了在近壁区计算上k-ω模型的优点和在远场计算上k-ε模型的优点，并且将湍流剪切应力的输送过程应用到湍流粘性系数的定义中，又增加了交叉扩散项，从而使SST k-ω湍流模型有了更广的应用范围。以SST k-ω湍流模型的输送方程为：

(3)

(4)

(5)

其中，Γ，Γk，Γω分别为速度u(v或ω)、湍动能k及比耗散率ω的有效扩散系数，其各自的定义为：

(6)

其中，μt为湍流粘性系数，其定义为：

(7)

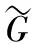
(8)

式(3)～式(8)中，ρ为空气密度；p为气体压强；μ为分子粘性系数；S为平均应变率的张量模量；F1，F2均为混合函数；σk，σω，α*，α∞，β*及βi均为湍流模型中的系数；σω,2，α1均为湍流模型常数；Si，Sk及Sω分别为各输送方程的自定义原项，各项定义详见文献[5]。

2 数值模型和边界条件的确定

2.1 数值模型

采用CFD商业计算软件Fluent对三维建筑物及计算域进行模拟。高层建筑物的尺寸为200 m×40 m×40 m。计算域根据数值风洞的计算要求，建筑物上游取4H，下游取10H，横向和纵向各取4H，其中，H为建筑物的高度，计算域的尺寸为2 800 m×800 m×800 m。

采用结构化网格对计算区域进行离散。结构化网格能够保证网格的质量，从而使结算结果更加精确。为了满足要求，建筑物表面最小的网格尺寸为0.01 m。最终模型划分的六面体网格总数为607万，计算区域划分的网格如图1所示。

为了与实验[6]进行比较，在数值风洞当中，我们根据相似理论对几何模型进行1∶400的缩尺。

2.2 边界条件

入口边界采用速度进流边界条件(velocity-inlet)，平均风速剖面和湍流风剖面采用Fluent提供的UDF(User-Defined Functions)编程与Fluent作接口实现。在两种不同的入口条件下，分别模拟大气边界层风速剖面指数分布，计算区域各边界条件的定义如表1所示。

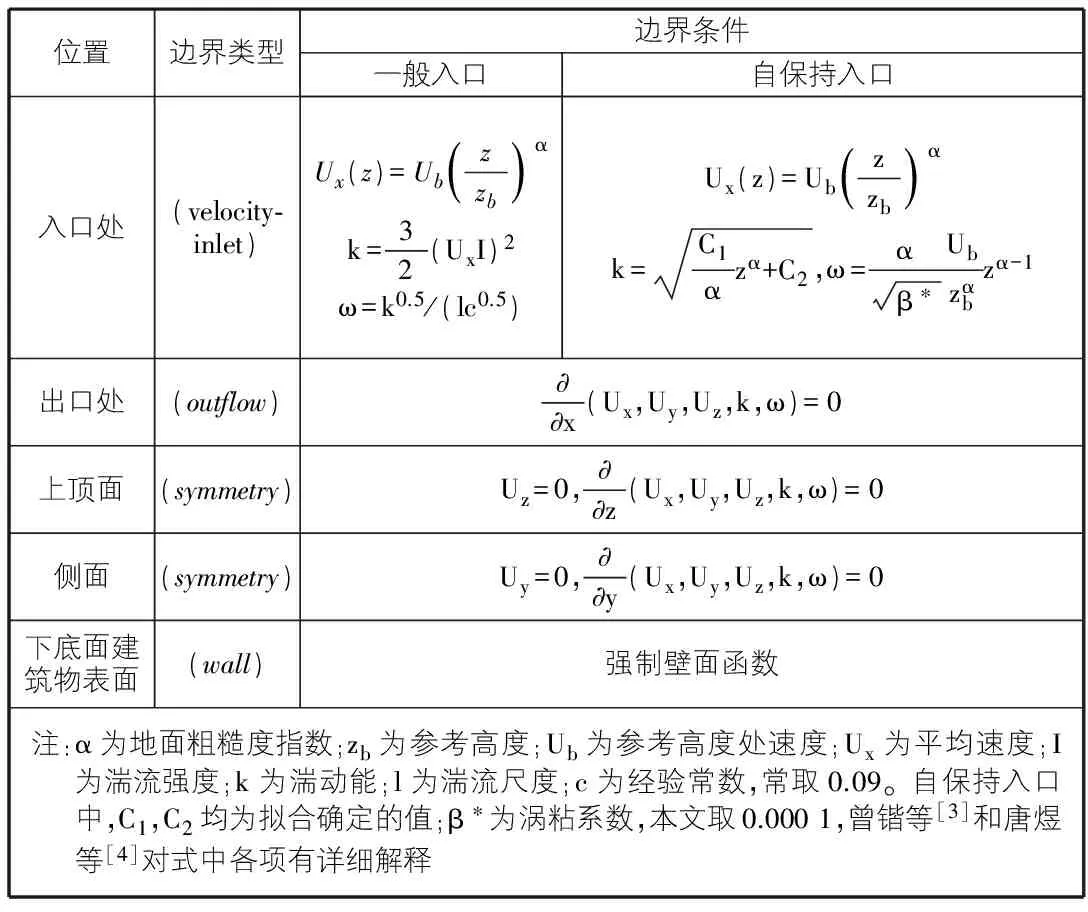
表1 边界条件

3 计算结果分析

3.1 平均风速和湍动能

图2给出了两种不同入口处平均风速和湍动能沿高度变化曲线的比较。由图2可知：1)未进行入口来流自保持时，在到达建筑表面之前，平均风剖面并没有太大的波动，在距离建筑物200 m处，平均风开始出现扰动。将入口来流进行入口自保持之后，在到达建筑表面之前平均风剖面都能够得到很好的保持。2)一般入口和自保持入口的湍动能有较大的差异。未进行来流自保持时，湍动能在200 m以上没有明显的改变，而在200 m以下，随着越来越接近建筑，湍动能越大，这表明来流耗散程度越来越大。将入口进行自保持处理之后，湍动能并没有明显的变化。

由于建筑物正是处于200 m以下的计算域内，所以湍动能的这部分改变会引起建筑物表面风压的变化。

3.2 压力等值线

量纲的压力系数Cp定义为:

(9)

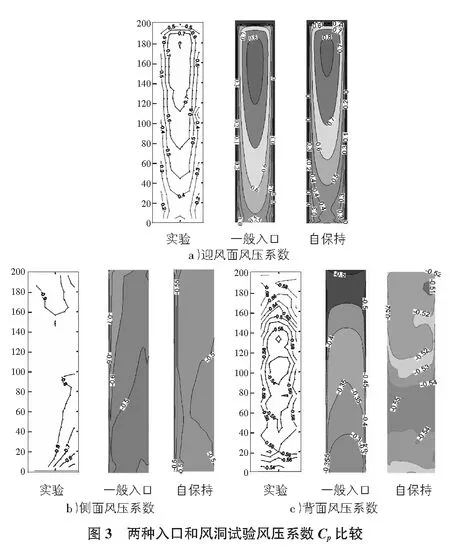
其中，p为相对压力；ρ为空气密度，取为1.225 kg/m3；u0为建筑物顶部的风速。两种入口的建筑物表面风压与风动试验的比较如图3所示。

迎风面和处于分离区的侧面的风压系数对比可以发现，两种情况迎风面的风压系数与实验值的趋势一致。但是比较而言，迎风面数值计算的结果稍微偏大，而侧面的数值计算结果偏小，这点在其他文献有所提及[7]。入口在进行自保持之后，迎风面风压系数更为接近实验值，而侧面的结果并没有改善，相反比一般入口更偏离实验值。

模型背面处于完全分离区，是难以准确模拟的部位，图3c)表明，两种入口的背面风压与实验值相比都有所差别，计算的两个结果之间相差不大。但是自保持入口得到的结果整体上与实验值相比较一般入口要稍好。

4 结语

1)基于Fluent SST k-ω湍流模型，在计算建筑物表面风压时，采用自保持入口边界条件，能够使建筑物上游平均风速和湍动能得到很好地自保持。

2)比较而言，入口采用自保持，迎风面风压能够得到较好的改善，与实验值更符合。但是在分离区的侧面和背面，两种情况相差不大。

3)大气边界层自保持方法可以应用到建筑物风压计算当中去，可以适当提高精度。但在自保持的公式拟合和系数选取上，要着重注意。

[1] Richards P J,Hoxey R P.Appropriate boundary conditions for computational wind engineering models using the k-ω turbulence model[J].Journal of wind engineering and industrial aerodynamics,1993(46):145-153.

[2] Menter F R.Zonal two-equation k-ω turbulence model for aerodynamic flows[J].AIAA Paper,1993(2906):1993.

[3] 曾 锴,汪丛军,黄本才,等.计算风工程中几个关键影响因素的分析与建议[J].空气动力学学报,2007,25(4):504-508.

[4] 唐 煜,郑史雄,赵博文，等.平衡大气边界层自保持问题的研究[J].工程力学,2014(10):129-135.

[5] FLUENT,Fluent 6.3 user’s guide[M].Labnon,New Hampshire.Fluent lnc,2006.

[6] Huang G.Probabilistic analysis of load effects on tall buildings under stationary and nonstationary extreme winds[D]. Texas Tech University,2008.

[7] Sun Eun K I M,Boysan F.Application of CFD to environment flows[J].Journal of Wind Engineering and Industrial Aerodynamics,1999(81):145-158.

The influence of the self-sustaining of atmosphere boundary layers on building wind pressure

Qin Gang Cheng Xu

(SouthwestJiaotongUniversity,Chengdu610031,China)

Using a atmospheric boundary layer self preservation method, and based on SST k-ω turbulence model, from the pressure contours, average wind speed and turbulence energy and other aspects, researched the building surface wind pressure, pointed out that the atmospheric boundary layer self preservation method could be applied to building wind pressure calculation.

computation wind engineering, SST k-ω turbulence model, surface wind pressure, pressure contour

1009-6825(2017)05-0048-03

2016-12-06

秦 刚(1989- )，男，在读硕士； 程 旭(1989- )，男，在读博士

TU311

A