灰色动态聚类法在大坝监测中的应用
2017-04-21蔡德所
蔡德所 章 聪
(1. 三峡大学 水利与环境学院, 湖北 宜昌 443002; 2. 三峡大学 土木与建筑学院, 湖北 宜昌 443002)
灰色动态聚类法在大坝监测中的应用
蔡德所1章 聪2
(1. 三峡大学 水利与环境学院, 湖北 宜昌 443002; 2. 三峡大学 土木与建筑学院, 湖北 宜昌 443002)
灰色动态聚类法采用“段”数据作为基本研究对象有别于常规聚类方法中的“点”数据,利用该方法对面板堆石坝面板挠度变形监测数据开展研究,可确定关键的面板变形段,需要重点监测和分析,同时结合matlab软件建立灰色模型GM(1,1)和多元回归模型对关键段监测数据进行预报拟合,结果表明,对于短期或者残缺的资料,利用灰色动态聚类法处理大坝监测数据具有便捷、高效的优点,模型预报结果拟合度较高.
监测; 面板变形; 灰色动态聚类; GM(1,1)模型; 多元回归模型
大坝安全监测的主要目的是掌握大坝的运行性状以及各监测量的变化趋势.随着现代监测技术的快速发展,大坝点式监测逐渐被分布式监测代替,大坝监测测点更加全面,常规的数据分析方法通常采用以点带面的方式进而得出大坝的运行状况,为了更加精确地反应大坝情况,本文在灰色理论[1]及模糊数学[2]的基础上,尝试将模糊数学与灰色理论相结合,形成灰色动态聚类分析法,对水布垭大坝面板变形监测数据进行聚类分析,然后通过最佳分类确定关键段.对关键段进行详细的分析不仅能减少工作量,还可以较以往点式分析能更好地掌握大坝的真实运行状况.
1 灰色动态聚类法的基本原理[3]
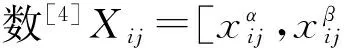
(1)
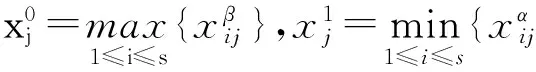
要对模糊类或者灰色信息进行科学准确的分类,我们通常用相似度或者距离法来计算指标值之间的相似程度,本文在比较了多种相似度公式的前提下,通过计算区间灰数最大最小法的相似系数从而计算出区间灰数向量间的相似度.区间灰数最大最小法的相似系数
(2)
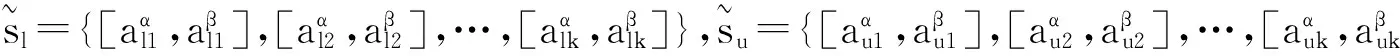
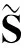
(3)
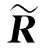
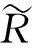
(4)
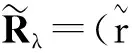
2 确定最佳分类数[6]
对于聚类分析中最佳分类的确定,本文源于数理统计中方差分析的启发,假设样品指标服从正态分布的条件,本文运用Mixed-F统计值来确定最佳分类数[6].
令
(5)
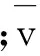
令
(6)
为混合F统计量,它同样服从自由度为(c-1,n-c)的F分布.
从上式可以看出,Mixed-F综合反映了所有变量的类内紧密程度与类间分散程度的统计量,采取倒数加权的形式,突出了较小的F(K)的影响,使分类的保证程度更高.
3 实例分析
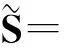
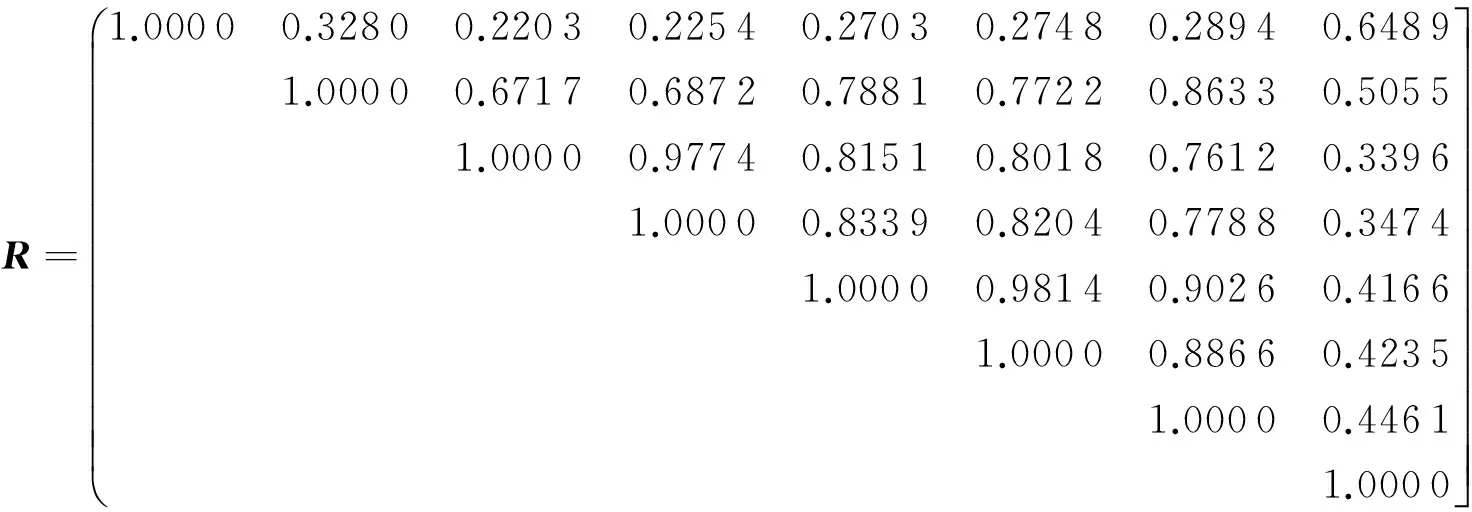
(7)
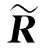
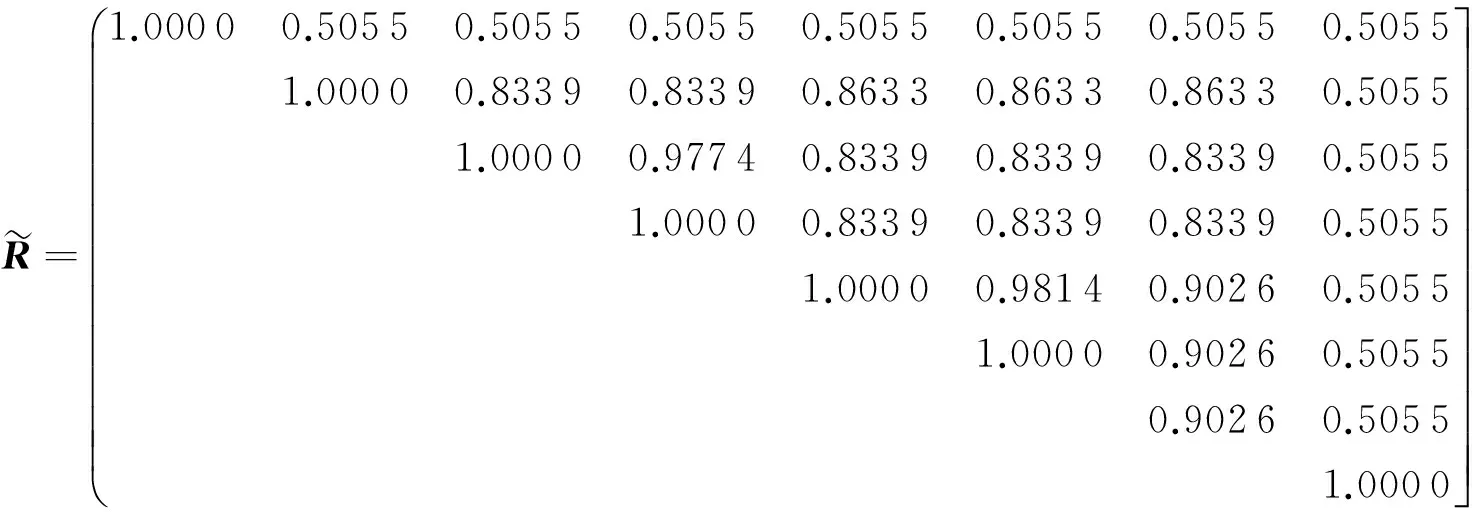
(8)
根据给定不同的阈值λ取得不同聚类结果见表1.
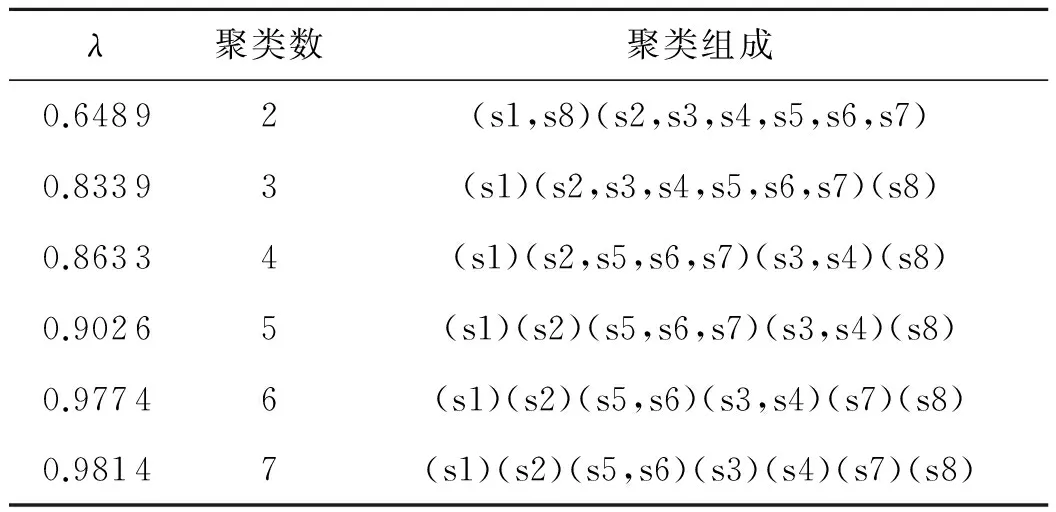
表1 不同的阈值λ取得不同聚类结果
根据公式(6)计算出不同分类数对应不同Mixed-F值见表2.

表2 不同分类数对应不同Mixed-F值
显然当样本分类数为6时,Mixed-F值最大,故取最佳分类数6为最终分类结果,见表3.

表3 最佳聚类结果
4 对关键段落进行拟合预测
现有的大坝监测资料分析方法有很多,比如多元回归分析方法、神经网络方法等.由于大坝面板的变形影响因素较为复杂,影响因子较多,面板变形与水位、温度、时效以及其它一些环境量的突变均有关系,比如突然的天气变化、降雨量等等,通常对大坝全部影响因子资料的收集较为困难,导致资料信息不够完整,对此,本文提出应用灰色理论原理,对面板监测资料进行分析,灰色模型就是通过少量的、不完全的信息,建立灰色微分预测模型,对面板变形发展规律作出模糊性的长期描述,灰色系统是既含有已知信息,比如温度、水位、时效,又含有未知信息或非确知信息的系统,本文应用灰色模型GM(1,1)和常规多元回归模型对2010年度水布垭面板坝共12期面板监测资料进行对比研究分析.
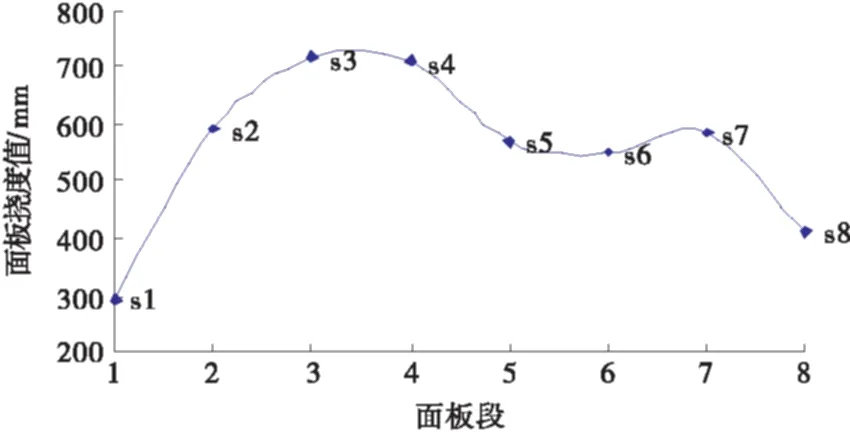
图1 2010年水布垭面板堆石坝面板平均相对挠度
如图1所示,第3类和第5类的样段(s3,s4,s7)作为挠曲线的极值点,正好位于“M”型挠曲线的两个波峰,说明了关键监测段应为第3类和第5类,同时也说明了聚类的合理性.对第3类(s3,s4)进行拟合预测,本文取s3段中的最大值作为研究对象用来反应s3、s4面板的情况,对于第5类样段s7,本文选取s7段中的最大值作为研究对象进行分析用来反映s7段面板的变形情况.
4.1 GM(1,1)预测模型基本方法[8]
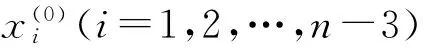
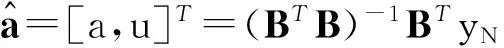
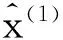
利用还原模型进行拟合预测.
利用Matlab软件建立GM(1,1)模型[9],对s3、s7面板段进行计算,求解出预测值,预测值与实测值如图2~3所示.
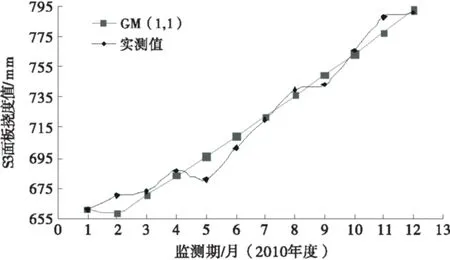
图2 面板监测段运用GM(1,1)模型的拟合曲线
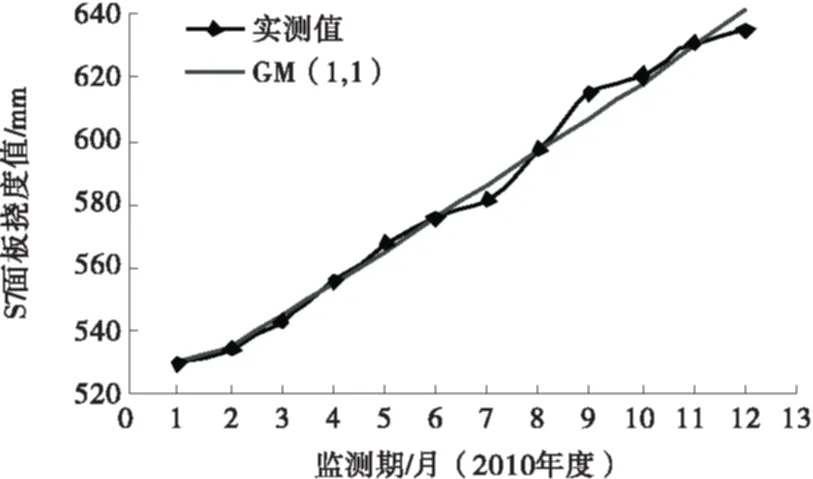
图3 面板监测段运用GM(1,1)模型的拟合曲线
4.2 多元回归分析方法[10]
多元回归分析法是研究多个自变量与因变量之间关系的方法,其实质其实为最小二乘法,需要事先建立统计模型,根据观测值求解出该统计模型的未知系数最优解,最后通过统计模型对观测值进行拟合和预报,在本文中,因变量为面板挠度值,自变量为水位、温度、时效3个因素,同时在参考过相关文献后,建立多元回归统计模型如下:
(9)
式中,H为上游水位;T为监测当天温度;q为时间(d).
利用Matlab软件建立多元回归统计模型,对s3、s7面板段数据进行拟合计算,得出的回归方程为:
Ys3=1.429×106-1.117×104×H+
(10)
Ys7=1.325×106-1.036×104×H+
(11)
同时,根据所得出的回归方程,分别代入环境因子,得出预测值如图4~5所示.
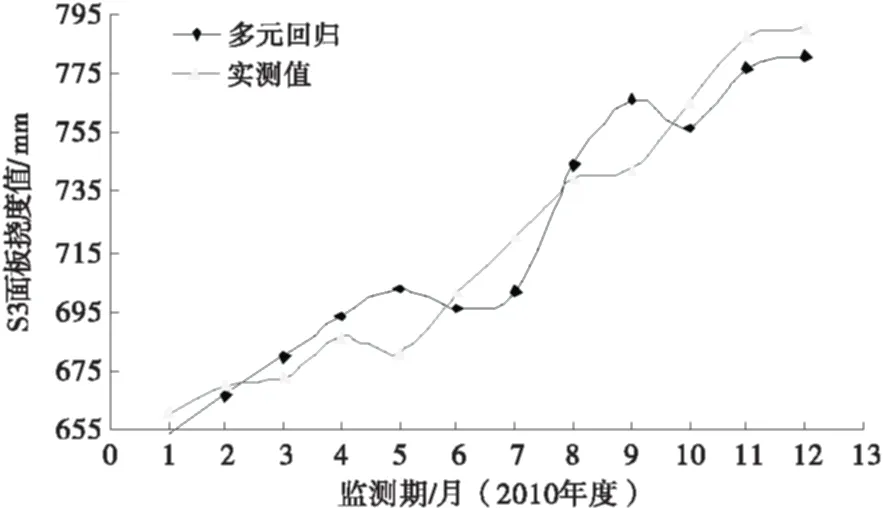
图4 面板监测段运用多元回归模型的拟合曲线
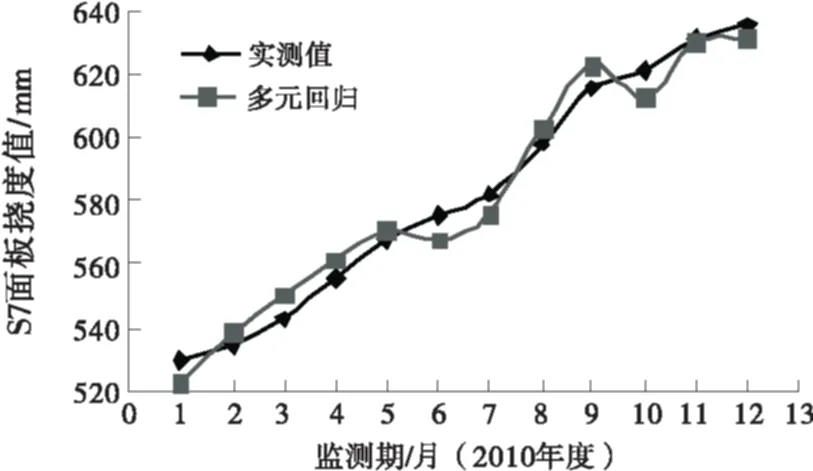
图5 面板监测段运用多元回归模型的拟合曲线
5 预测精度对比分析
为了分析所选用的两个模型的精度,本文选取均方根误差RMSE和相关系数R对GM(1,1)模型和多元回归模型进行检验,结果见下表,由表可以看出,不论是在对s7面板段还是在s3面板段的资料分析中,GM(1,1)模型的相关系数较多元回归模型的相关系数大,且GM(1,1)模型的均方根误差较多元回归模型的要小,由此可以推断,多元回归模型作为一种常规的统计预测模型,其精度可能受到所分析资料的信息数量及其完整性的影响,数据信息量越大,其拟合精度越高,同时依靠经验选择多元回归统计模型表达式,对拟合精度也会造成影响,针对大坝变形资料分析,往往收集完整的资料信息难度较大,且各个影响因子之间也存在着一定的内在关系,而灰色理论分析法正适合对于信息不够完备、各种因素之间隐含联系的资料进行分析,因此在这种条件下,运用灰色理论对大坝资料进行分析显示出其独特的优势.
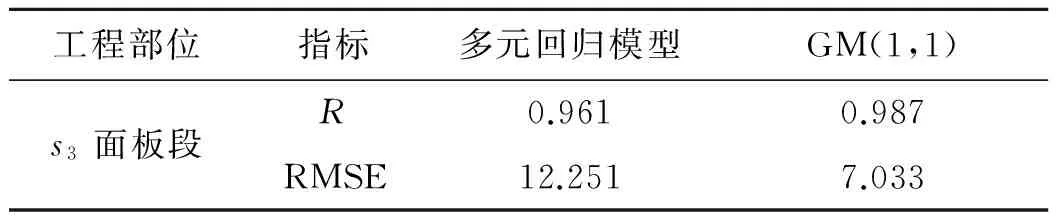
表4 两种模型在s3面板监测段的拟合精度
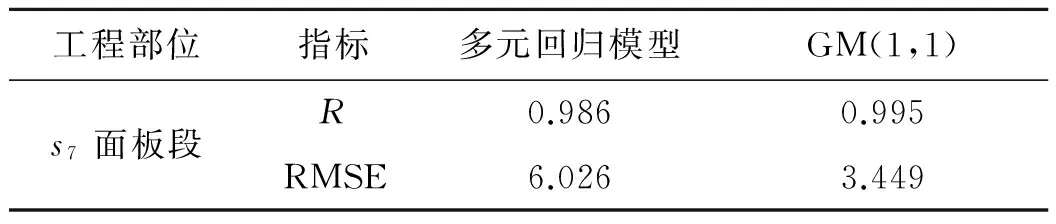
表5 两种模型在s7面板监测段的拟合精度
6 结 语
在对水布垭面板坝面板挠度变形数据分析的基础上,研究并应用了灰色动态聚类的方法,采用“段”数据作为基本研究对象较常规聚类方法中的“点”数据,更加全面地体现了大坝面板变形的情况.对比分析GM(1,1)模型和多元回归模型在对面板关键监测段的数据拟合预报,结果表明,在资料信息不够完善、内在影响因素较多的情况下,GM(1,1)模型的拟合精度更高,可以有效地预报面板挠度变形.将灰色动态聚类与GM(1,1)结合起来处理大坝变形监测的数据,能提高工作效率,随时掌握大坝运行情况.
[1] 易德生,郭 萍.灰色理论与方法[M].北京:石油工业出版社,1992.
[2] 楼世博,孙 章,陈化成.模糊数学[M].北京:科学出版社,1983.
[3] 丁 力,田林亚,范雷刚,等.基于灰色聚类法和灰色关联分析的大坝安全评价[J].测绘工程,2015,24(4):67-73.
[4] 李 星.模糊聚类与灰色聚类在我国证券投资中的应用[D].株洲:湖南工业大学,2012.
[5] 杨俊杰.灰色聚类与灰靶决策的算法研究[D].厦门:厦门大学,2009.
[6] 孙才志,王敬东,潘 俊.模糊聚类分析最佳聚类数的确定方法研究[J].模糊系统与数学,2001,15(1):89-92.
[7] 光纤传感技术在大坝工程中的应用[M].北京:中国水利水电出版社.
[8] 卢 懿.灰色预测模型的研究及其应用[D].杭州:浙江理工大学,2014.
[9] 宋叶志,贾东勇.MATLAB数值分析与应用[M].北京:机械工业出版社.
[10] 吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003.
[责任编辑 王康平]
Application of Grey Dynamic Clustering Method to Dam Monitoring
Cai Desuo1Zhang Cong2
(1. College of Hydraulic & Environmental Engineering,China Three Gorges Univ., Yichang 443002, China;2. College of Civil Engineering & Architecture,China Three Gorges Univ., Yichang 443002, China)
Grey dynamic clustering method using “section” data is different from conventional clustering methods used in the “point” data as a basic research object; the method is used to carry out the research on the deformation monitoring data of the deformation of the face slab of the face slab rockfill dam. The determination of key section of the panel deformation sections, it needs to be focused on monitoring and analysis; at the same time, the GM (1,1) model and multiple regression model are established by using MATLAB software, which is used to forecast the key segment monitoring data. The results show that the grey dynamic clustering method is used to deal with the short-term or incomplete dam monitoring data, which has the advantages of convenient, high efficiency and high precision.
monitoring; panel deformation; grey dynamic clustering; GM (1,1) model; multiple regression model
2016-06-27
国家自然科学基金重点项目(NO.51439003)
蔡德所(1952-),男,教授,主要研究方向为光纤传感技术及其在水利水电工程中的作用.E-mail:caidesuo@vip.163.com
10.13393/j.cnki.issn.1672-948X.2017.02.006
TV698.1
A
1672-948X(2017)02-0024-05
