基于奇异值分解模型的在线实时推荐的隐私保护

□路应金 杜素娟

[电子科技大学 成都 611731]

基于奇异值分解模型的在线实时推荐的隐私保护

□路应金 杜素娟

[电子科技大学 成都 611731]

利用缩减的奇异值分解更新算法和随机技术提出了一个基于奇异值分解模型的在线推荐的隐私保护方法，将新数据混合到原始数据中保护消费者在线购物的隐私数据。实验结果表明，我们提供的模型可以保证数据高效性和更低概率的隐私泄露，并且预测的精度仍然很高，对于实现消费者网上隐私保护有重要的指导意义。

奇异值分解；隐私保护；实时推荐；协同过滤

引言

伴随着电子商务的快速发展，个性化推荐系统成为电子商务企业在线推销商品的有力工具。亚马逊、京东通过向消费者推荐感兴趣的产品提升在线商品销售的选择。推荐系统是通过构建消费者的购物模式利用相关算法来预测消费者的购物偏好的系统。从上世纪90年代中期就有很多关于推荐系统的论文发表[1]，学者们将其算法和模型应用于现实生活中，大多数的推荐系统源于协同过滤算法[2～3]。协调过滤算法是推荐算法中应用得最为广泛和成功的一种算法[4～5]。协同过滤技术也是个性化推荐中应用最成功的技术[6～7]。协同过滤技术可以分为两大分支：邻近算法和潜在因子模型[8]。奇异值分解算法是基于潜在因子模型的一种算法[9]。

隐私保护的协同过滤推荐研究致力于在确保高质、高效地产生推荐的同时有效地保护参与方的隐私[10]。奇异值分解模型是协同过滤算法中重要的一种典型算法[11]，是一种基于数据扰动的方法[12]。在推荐系统中，用户并不参与原始数据的处理，他们将自己的数据发送给服务器，然后服务器进行数据的协同过滤。Polat和Du将随机扰动加入到基于协同过滤技术的奇异值分解算法中，以此来构建隐私保护系统[13～14]，把统一的或者高斯分布的扰动加入到用户的真实偏好中，然后服务器预测这些扰动数据的未知偏好。在这种结构下，数据拥有者也要注意数据的快速更新，以及随着数据更新，对隐私的保护水平还可以保持在一个相对合理的位置。Stewart研究了奇异值分解算法中的扰动理论以及其在信号处理中的应用[15]。Brand论证了一个奇异值分解算法的快速降低矩阵的秩的修正算法[16]，Tougas和Spiteri证明了局部奇异值分解更新算法时需要进行正交三角分解以及完全奇异值分解时计算并不复杂[17]。Wang等提出了一种改进的奇异值分解模型，本文改进了模型的奇异值分解更新算法，加入了随机扰动和后期的加工。

一、模型的构建

（一）基于潜在因子模型的原始奇异值分解算法

潜在因子模型[18]主要致力于用户评分矩阵的降低维度上，以此来发掘一些潜在因子，这些因子使用最少的扰动数据可以最好地诠释用户的偏好，我们可以充分利用这些因子来近似估计原始评分值。在Paterek的基于潜在因子模型的奇异值分解算法中，将用户评分矩阵因式分解成更低的评分矩阵，用户元素矩阵UF和商品元素矩阵IF。每一个用户i和商品j可以分别表示成一个f维度矢量UFi（矩阵UF的第i行）和IFi（矩阵IF的第j列）。我们通过计算向量UFi和IFi的内积来预测第i行第j列元素的评分。

首先，应用奇异值分解算法计算稀疏矩阵R，填补所有的缺失值，将缺失数值设置为零，然后得到用户向量和商品向量。

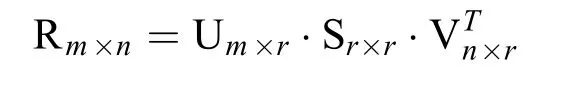
这里的U和V是标准正交矩阵，S是对角线上的元素为奇异值的对角阵，且矩阵S的秩为r。

利用Berry的大范围的稀疏奇异值算法[19]，当分解评分矩阵时，维度f（f不大于r）比较容易定义，因此用户元素矩阵和商品元素矩阵也可以表示为：

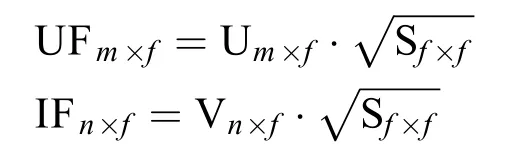
（二）问题描述

假设数据拥有者有一个用户评分矩阵，R∈Rm×n，其中有m个用户和n个商品，rij表示用户i对商品j的评分。有效的评分值取值范围在不同网络的情况是不同的，一些网络评分值从1～5，1是最低评分表示不喜欢，5是最高评分代表最受欢迎，而一些网站用-10～10来评分，其中-10表示最低分，0表示中立评分，10为最高评分。

用户的原始评分矩阵包含用户对商品的真实评分，我们可以由此确定用户的购物模式。这些模型可能泄露了某些用户的隐私，所以在毫无隐私保护措施的情况下放出用户的原始评分数据将会导致隐私的泄露。在放出用户原始评分数据之前插补矩阵然后扰乱它是一种可行的保护用户隐私的方法。因为所有的商品都随着评分做了标记，所以存在缺失数值就无法分辨哪些商品已经评分。在这个过程中，插补估算缺失的评分数据，隐藏用户对特定商品的喜好，同时这个扰动使得用户对特定商品的喜好变得模糊不清。

当有新的用户交易数据出现时，新的行向量，定义为T∈Rp×n，添加到原始矩阵R中，

类似的，当有新的商品交易数据出现时，新的列向量，定义为G∈Rm×q，添加到原始矩阵R中，

为了保护用户隐私，新的评分矩阵在放出之前必须经过加工。Tr∈Rp×n表示处理过的新的行向量，Gr∈Rm×q表示处理过的新的列向量。

（三）数据更新模型

本部分主要介绍在数据更新过程保护隐私的协同过滤算法中的数据更新模型。通过在以下三个方面用户的隐私：缺失数值的插补，随机扰动数据和缩减的SVD算法。插补值的步骤可以保护用户已评分的隐私信息。但是由于单一的传统的插补值会产生相同的值并以此填入空白项，这样的矩阵容易被攻击。因此我们增加了另外一种隐私信息，即用户对特定商品的实际评分值。在这种情况下，随机性和缩减的SVD技术可以作为解决问题的第二种扰动项。一方面，随机扰动可以一定程度上改变评分值，剩余的分布不改变。另一方面，所用的SVD技术是一种理想的数据扰动的方式，这种技术可以捕获矩阵的潜在性质并且消除无用的扰动。对于给定的已选好的缩减排列，SVD可以在数据隐私和效用之间保持很好的平衡。

正如前面部分的陈述一样，新的数据可以作为矩阵新的行向量或者列向量。把这些新数据添加到原始矩阵R，然后进一步扰乱数据来保护用户隐私。相应的，我们提出的模型也可以在行向量或者列向量单独更新的时候使用。

1.行更新

在等式（1）中，将向量T加入R中，得到的新矩阵R’是一个（m+p）×n的矩阵，假设缩减矩阵R的k阶SVD先前已经计算过，

其中，Uk∈Rm×k，Vk∈Rn×k是正交矩阵；是最大有K个奇异值的对角线矩阵。

我们上一部分提到的，用户评分矩阵在因式分解之前是一个不完全的矩阵，需要提前插入缺失值，例如，插入每个商品的平均评分值，这些平均值用来帮助更新SVD。

对于新的行向量T，在加入现存矩阵之前，先插入缺失值，用插入数值填补空白项，插入数值来自于现存矩阵和新评分数据的平均值。列的均值由下式计算：

新的列的平均值不影响原来的矩阵，因此，拥有扰动数据的第三方平台和数据拥有者只需要释放扰动的新数据，不需要改变列均值。

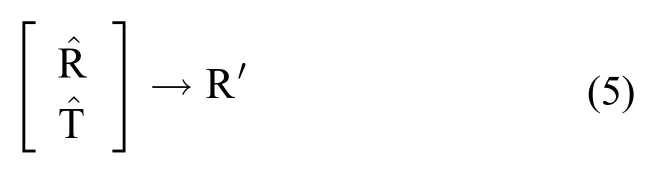
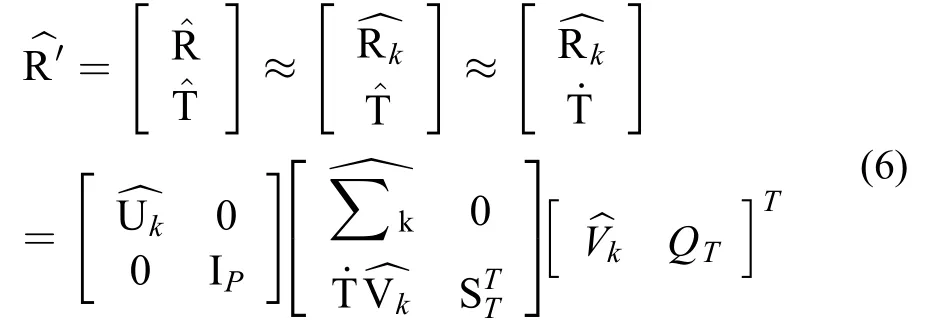
这个k阶奇异值分解矩阵在下面的矩阵中计算得到

由于(k+p)是一个很小的值，奇异值分解的计算过程很快，所以我们用矩阵缩减的奇异值分解来代替完整的分解

在协同过滤算法中，所有项的值的取值范围应该是有效的。例如，在MovielLens数据中的r的取值范围应该是0＜r≤5。所以，在得到新的新矩阵之后，接下来的一步就是应用有效取值范围，使得合理值取代所有的非有效值

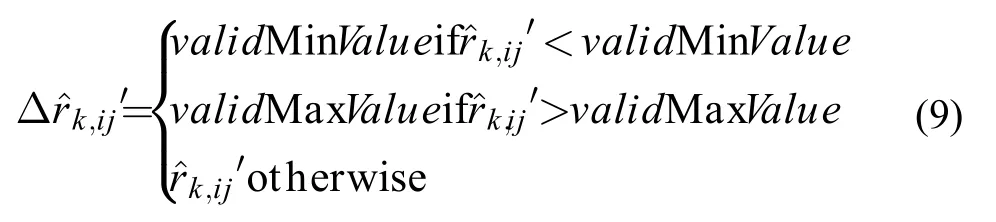
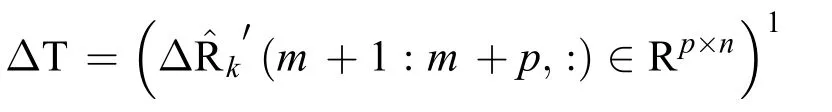
以下总结了行更新时的奇异值分解算法步骤

2.列更新

列更新类似于行更新，但是两者有一些不同。在新的用户评分矩阵中，用商品平均值来填补缺失值。在行更新中，当新用户增加时均值改变；但是列更新中，均值仅仅取决于新商品。由于这种特性，列更新时不必保持一个商品的均值矢量。

以下总结了行更新时的奇异值分解算法步骤

数据拥有者应该持有更新元素矩阵，无论是列更新还是行更新，并且插入新的数据矩阵。当用户发生更新时，这个更新商品均值也应该由数据拥有者持有。

正像在两种算法中表述的，在保护用户隐私方面，结合使用了三种插入数值技术。初始插入数值替补了所有的缺失值。在插入数据中加入随机扰动使得插入数值之间彼此不同。缩减的奇异值分解算法消除了数据的繁琐性，这个过程保护了数据的有效性同时保护了数据的隐私。三种技术结合起来在不同方面保护隐私。

图1 奇异值分解算法流程示意图

二、模型评估

（一）预测模型和误差检测

因为奇异值分解模型不能解决缺失数值问题，如果没有预处理值的话那些缺失数值就会为零。经典的填补缺失数值的方法就是使用商品的均值。

假设p’ij是通过基于协同过滤算法的奇异值分解模型得到的预测值，为了确保预测的评分值在有效范围内，我们需要做一些边界范围的检测：

当我们检测预测的准确度时，用户元素矩阵UF和商品元素矩阵IF首先来自于样本集，然后对于在每个样本集里的评分集，我们对所有的评分值计算出相应的预测值，并且检测误差值，以及绝对平均误差，误差值越小越好。计算公式如下：

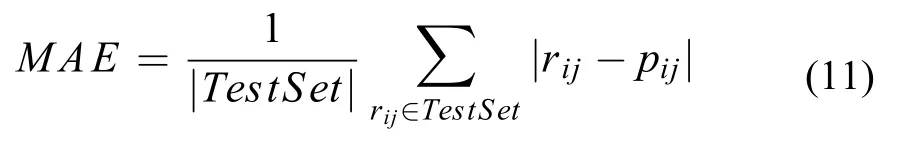
（二）隐私估计

隐私水平是一个度量，表示我们可以通过给出的随机变量X来估计随机变量Y的取值范围

隐私估计是由阿格瓦拉和阿加沃尔提出的，并且波拉提尔应用于协同过滤算法中。阿格瓦拉和阿加沃尔还提出了已知X条件下的Y的缺失值的条件隐私的估计[20]。

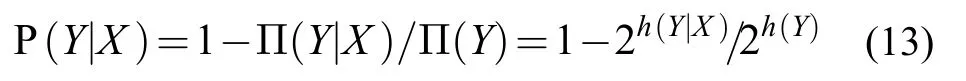
（三）评估策略

为了检测何时重新进行奇异值分解，我们把评分矩阵的数据集用一个专门的比率ρ1分解成两个子栏目。 假设第一个的ρ1已经处理过了，剩下的数据然后更新进去。然后计算矩阵中的k阶奇异值分解和商品平均值矢量。我们命名K阶矩阵的近似值为开始矩阵。我们利用这些数据结构作为公式（10）的输入。我们期望得到的结果随着分流比率不同而变化。如果结果与我们预先确定的临界值偏离太远，或者结果演变的更慢或者开始在某些点上下降，我们将会进行重新的计算。

然而，我们在样本集中保留的60%行向量不仅仅只有一次更新，因为现实当中程序通常是逐步增加的。本次实验当中，分几次向60%的行向量添加到开始矩阵，取决于另一个分流比ρ2。比如说，如果ρ2=1/10，增加十次新数据到开始矩阵。最后由开始矩阵与十次增加矩阵之和得到的矩阵就是扰动和更新矩阵。

三、数据分析

本次实验的数据取自MovieLens数据库和Jester数据库。我们选取MovieLens数据库的10万条评分集，其中有943位用户和1682件商品。这十万条评分，评分值从1～5，可分为有8万评分的样本集和2万评分的测试集，两个集合都比较稀疏。

Jester数据库来自一个笑话推荐系统的网站，我们选取其中的数据集，包括24983位用户和100条笑话以及1810455个评分，评分值从-10～+10。我们随机抽取其中的80%作为样本集，其余的作为测试集。与MovieLens数据库相比，Jester数据没有那么稀疏。

（一）奇异值分解算法中的缩减的秩（k）的选取

在实验中我们从{2,5,…,25,50,100}中选取k值，然后计算相应的绝对平均误差。MovieLens的结果如图2，这个曲线显示MAE随着k值的变化而变化，并且在k=13的时候有最小值。类似的Jester的实验结果显示k=11的时候有最小的MAE值。因此，我们在MovieLens数据集里面选择k=13，Jester数据集里面的k=11是合理的。

（二）分流比ρ2

在本次实验当中，ρ1是固定的40%，也就是样本集里的40%的数据作为起始矩阵，余下的60%的会加到矩阵里面。分别设置ρ2为1/10,1/9,1/8,…,1/2,1。

图3描述了不同的分流比ρ2对应的时间成本。行更新用Row代表，列更新用Column代表。为了消除其中的随机影响，设置μ和σ为零。

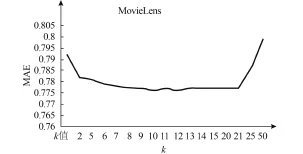
图2 不同秩k值下的MAE变化图

图3 随着分流比ρ2变化的时间成本图

MovieLens数据的曲线通常是随着分流比的增大而上升的趋势，行更新的时间比列的更新的更长一些。在Jester数据中，当ρ2=1/3时，列更新的时间最短，行更新的时间比列的更新较短，而且在每次循环中更新的数据越少，需要的时间越短。分流比不能仅仅通过时间因素来确定，实验中的预测精确度和隐私保护水平也是关键。

图3表明更新的时间取决于行和列的维度。比如说，MovieLens数据集有列比行多，Jester数据的列比行少。每一步的行和列的算法显示，当列数比行数多的时候，因为有更高的维度和，算法中的第一步和第三步需要更多时间。与插入数据的时间成本相比，进行原始样本集的奇异值分解，该方案在行和列更新上运行更快。

图4显示，不同分流比ρ2对应的绝对平均误差保持不变，说明更新数据的预测精确度受ρ2的影响不大，类似的隐私水平结果也是如此，如下图4所示。

通过以上的分流比ρ2的实验结果，我们设定在MovieLens数据中，行更新和列更新时ρ2=1/10，在Jester数据中行更新是设定ρ2=1/10，列更新时设定ρ2=1/3 。

图4 随着分流比ρ2变化的MAE图

（三）分流比ρ1

由于SVD算法固有的特性，每次运算中少不了误差。数据的拥有者应该意识到合适的时间对整个数据重新进行奇异值分解以便保证数据的质量，这个问题就是通过分流比ρ1来解决。

不同ρ1下更新数据的时间成本如图5所示，我们预期更新的行或列数据越少花费的时间越少。但是，随着分流比的不同，相应的行更新和列更新的时间成本保持不变。

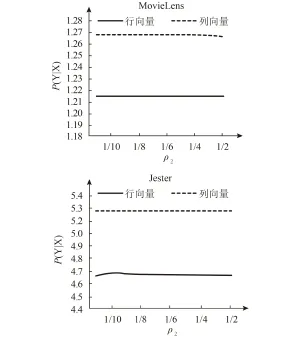
图5 随着分流比ρ2变化的隐私水平图

图6表示了绝对平均误差，MovieLens数据的曲线在航更新中有一个下降的趋势，但是在列更新中保持稳定。

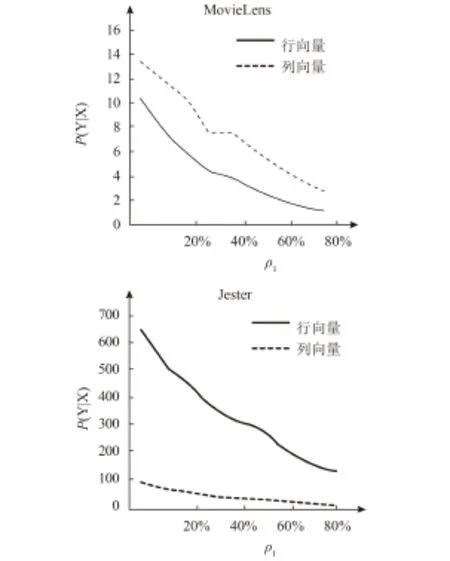
图6 随着分流比ρ1变化的时间成本图

在Jester数据中有所不同，随着分流比ρ1的增加绝对平均误差在列更新中有下降趋势，在行更新中保持稳定。这说明起始矩阵的评分值越少，预测模型刻画用户偏好的精确度越低，因此导致了更低的预测精准度。关于行和列对绝对平均误差的影响，取决于行和列的维度。因为在一个评分矩阵中的信息总量是确定的，假设每个矩阵之间的输入量是相同的，用户的数目越少，每个用户贡献的信息就越多。比如，在MovieLens数据中，行维度比列维度少，因此用户比商品扮演更重要的角色，因为用户比商品少，所以每个用户贡献的信息量比每个商品多。因此随着用户书面的增加，绝对平均误差减少了。在Jester数据中正好相反，行维度比列的多，因此列向量对于误差更为关键。如图7，与未更新的样本集的绝对平均误差MovieLens数据的0.7769和Jester数据的3.2871相比，当更新模型的ρ1为40%时，MovieLens数据的行更新为0.7951，列更新为0.7768和Jester数据的行更新为3.2870，列更新为3.3221，绝对平均误差保持在很好的水平，预测模型可用。

图8展示了随着分流比变化的隐私水平，起始矩阵中的数据越多隐私水平越低，数据越多，尤其是用户越多，对建构模型的贡献越多，泄露的隐私也就越多。在本次实验中，行更新的隐私水平都比列更新高，变化速度都比列的更新快。隐私在更新过程中至关重要。在已知扰乱的更新数据（X）时，得到的样本集数据的隐私的缺失值（Y）的结果如图9所示。

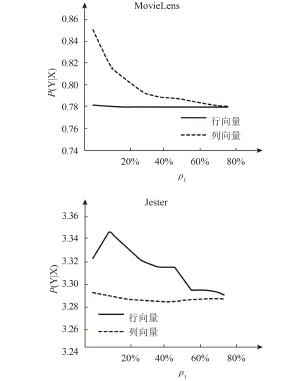
图7 随着分流比ρ1变化的绝对平均误差图

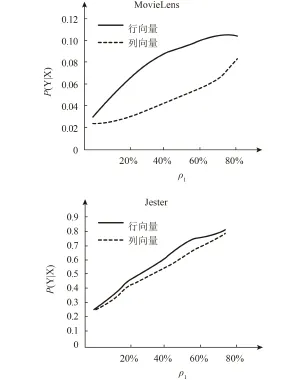
图8 随着分流比ρ1变化的隐私水平图

随着分流比的增大，隐私的缺失数值增大，隐私水平减小。两个曲线看起来是相反的。

从图6和图7可以确定整个数据重新进行奇异值分解的时间，由于当ρ1大于等于50%之后绝对平均误差下降的很慢，并且隐私保护水平曲线的斜率没有显著的变化，所以重新计算时的ρ1设定为50%。

（四）数据更新中的随机性

随机技术还未应用到我们提出的数据更新模型当中，但是随机性还是对于数据的质量和隐私的保护很重要的。一下的实验当中，ρ1是不变的值40%，ρ2是固定值1/9，我们试着设置μ在{0，1}中取值，σ在{0.1，1}当中取值。实验结果如表1所示。

图9 随着分流比ρ1变化的隐私缺失值图

表1 数据更新过程中的随机性因素

在这个表格中，随机的行更新和列更新与没有随机因素的进行比较。在数据更新前加入了随机扰动的新数据，隐私量和都有一定程度的提高。但是，数据的有效性略有下降，MAE也有所增加。因此，应该在数据的效用和数据的隐私之间权衡，选择参数。而且，结果显示期望μ比标准差σ更能影响实验结果，所以我们优先考虑μ。

在基于数据更新模型的奇异值分解算法中，我们采用随机技术作为一个辅助的步骤，以便更好地保护隐私。在奇异值算法更新前插入数据是随机的。因此，算上奇异值分解，有两次数据的扰动，可以提高隐私保护水平。同时，通过奇异值分解获取的潜在因子，我们可以保留关键的信息，确保推荐数据的质量。

四、结论

本文提出了一个基于协同过滤技术的隐私保护数据更新模型，这个模型是一个基于随机技术的增量的奇异值分解算法，可以用来更新增量的用户商品矩阵同时保护隐私。这个模型试着从三个方面保护消费者的隐私，分别是缺失数值的插入，随机地扰动和缩减的奇异值分解技术。实验结果表明，我们提出的模型可以快速地将更新的数据加入到现存的数据中，而且在保护隐私的同时推荐的精确度依然很高。

[1]ADOMAVICIUS G,TUZHILIN A.Toward the Next Generation of Recommender Systems: A Survey of the State-ofthe-Art and Possible Extensions[J].IEEE Transactions on Knowledge and Data Engineering,2005,17(6):734-749.

[2]GOLDBERG D,NICHOLS D,OKI B,TERRY D.Using Collaborative Filtering to Weave an Information Tapestry[J].Communications of the ACM,1992,35:61-70.

[3]KONSTAN J,MILLER B,MALTZ D,HERLOCKER J,et al.GroupLens: Applying Collaborative Filtering to Usenet News[J].Communications of the ACM,1997,40:77-87.

[4]黄宇.基于协同过滤的推荐系统设计与实现[D].北京: 北京交通大学,2015.

[5]刘青文.基于协同过滤的推荐算法研究[D].北京: 中国科学技术大学,2013.

[6]姚婷.基于协同过滤算法的个性化推荐研究[D].北京: 北京理工大学,2015.

[7]沈键.电子商务的个性化协同过滤推荐算法研究[D].上海: 上海交通大学,2013.

[8]KOREN Y.Factorization Meets the Neighborhood: a Multifaceted Collaborative Filtering Model[C]// The 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Las Vegas: Nevada,2008: 436-434.

[9]SARWAR B,KARYPIS G,KONSTAN J,RIEDL J.Application of Dimensionality Reduction in Recommender Systems[J].In Acm Webkdd Workshop,2000.

[10]张锋,孙雪冬,常会友,赵淦森.两方参与的隐私保护协同过滤推荐研究[J].电子学报,2009(01): 84-89.

[11]PATEREK A.Improving Regularized Singular Value Decomposition for Collaborative Filtering[J].Proceedings of KDD Cup and Workshop,2007(8):39-42.

[12]李光,王亚东.一种改进的基于奇异值分解的隐私保持分类挖掘方法[J].电子学报,2012(04): 739-744.

[13]POLAT H,DU W.Privacy-Preserving Collaborative Filtering [J].International Journal of Electronic Commerce,2005,9(4):9-35.

[14]POLAT H,DU W.SVD-based Collaborative Filtering with Privacy[J].ACM Symposium on Applied Computing,2005,1:791-795.

[15]STEWART G.Perturbation Theory for the Singular Value Decomposition [J].SVD &Signal Processing II Algorithms Analysis &Applications,1996,13(9):99-109.

[16]BRAND M.Fast Low-Rank Modifications of the Thin Singular Value Decomposition [J].Linear Algebra and its Applications,2006,415(1):20-30.

[17]TOUGAS J,SPITERI R.Updating the Partial Singular Value Decomposition in Latent Semantic Indexing [J].Computational Statistics &Data Analysis,2007,52: 174-183.

[18]KOREN Y.Factorization Meets the Neighborhood: a Multifaceted Collaborative Filtering Model[C]// the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Las Vegas: Nevada,2008:436-434.

[19]BERRY M.Large-scale Sparse Singular Value Computations [J].International Journal of High Performance computing Application,1992,6(1):13-49.

[20]ADOMAVICIUS G,TUZHILIN A.Toward the Next Generation of Recommender Systems: A Survey of the State-ofthe-Art and Possible Extensions[J].IEEE Transactions on Knowledge and Data Engineering,2005,17(6):734-749.

Privacy Preservation of Online Real-Time Recommendation Based on the SVD Scheme

LU Ying-jin DU Su-juan
( University of Electronic Science and Technology of China Chengdu 611731 China)

The most personalized recommendation method research of online shopping faces challenges about how to ensure the validity of data during the data sharing process and protect users' personal privacy.In this paper,we propose a privacy preserving scheme of online recommendation based on the SVD algorithm by the truncated SVD update algorithms and randomization techniques.It turns out that the proposed scheme can conduct data efficiently and protect data privacy effectively.It is of important guiding significance for privacy preserving of online consumers.

SVD;privacy preservation;real-time recommendation;collaborative filtering

G206.2

A

10.14071/j.1008-8105(2017)02-0074-08

编 辑 何婧

2015-11-25

国家自然科学基金（71372140）.

路应金（1964-）男，博士，电子科技大学经济与管理学院副教授；杜素娟（1993-）女，电子科技大学经济与管理学院硕士研究生.