三角网格文件的格式处理在3D打印技术中的应用
2017-04-21申作林沙晨明
申作林,沙晨明
(哈尔滨理工大学,哈尔滨 150040)
三角网格文件的格式处理在3D打印技术中的应用
申作林,沙晨明
(哈尔滨理工大学,哈尔滨 150040)
三维模型是计算机图形学重要的组成部分,用网格描述的三维模型的表示又是3D打印技术应用的先决条件,而对三角网格文件数据结构的认识将会直接影响到三维模型的分析处理。常用模型数据文件格式的提出,对扩充计算机图形学具有重要意义。在详细了解3D打印流程基础上,详细分析常用基于三角网格文件的数据结构,针对目前OFF模型文件组织结构的定义没有形成系统的规范问题,完成一种OFF文件网格模型数据结构的定义,提出模型互转思想,设计一种转换算法并进行3D打印实验验证结果。
计算机图形学; 格式转换;三维模型;3D打印;三角网格文件
三维模型是计算机图形学中的重要组成部分,目前随着3D打印技术的兴起,三维模型在计算机应用领域的研究中也扮演了更重要的角色。3D打印技术是制造业正在飞速发展的一项新兴技术,被称为“具有工业革命意义的制造技术”。美国《时代》周刊也将3D打印列为“美国十大增长最快的工业”之一。对于这一空前的技术而言,它有着必然的优势,如:工业制造上无须模具即可加工、产出品多样化、支持个性定制、降低技术门槛等。然而,在这种优势下也存在一系列问题,如:难以寻找具有优良性能的可打印耗材、打印经济代价昂贵、打印操作过于复杂、用于打印的模型冗杂且处理方式不规范导致打印效率低下等。针对3D打印模型冗杂这一问题,本文将简述3D打印的常规流程,提出“云制造+3D打印”的新型模式,论述常见三角网格模型文件的数据结构,针对OFF模型文件的组织结构设计模型转换算法,通过实验做出结论。
1 3D打印流程简述
对3D打印流程的详细分析,是实现3D打印流程细节优化的最根本前提。传统上认为,3D打印可大致分为六个部分,如图1所示。
在这六个部分中,前四项是数字几何处理部分,在这里不妨把这四部分称作“软处理”部分,而后两部分为硬件相关部分,称作“硬处理”部分。由“软”、“硬”的划分可见,三维模型的处理在3D打印应用中的重要性。
“云时代”的到来给制造业带来了一种全新的流程模式,传统的3D打印流程未能体现“云时代”的灵活性和多变性,那现在我们不妨思考一种全新的流程模式: 云制造+3D打印。在该模式下,通过基于Web的模型操作平台处理欲打印的三维模型,亦可通过平台结合格式转换器转换文件格式,上传至三维模型库或下载至本地,连接3D打印设备完成操作,如图2所示。在这种模式下,不仅实现了制造的云处理,而且利用OFF文件模型库占用空间少这一特点,实现了资源的节约。
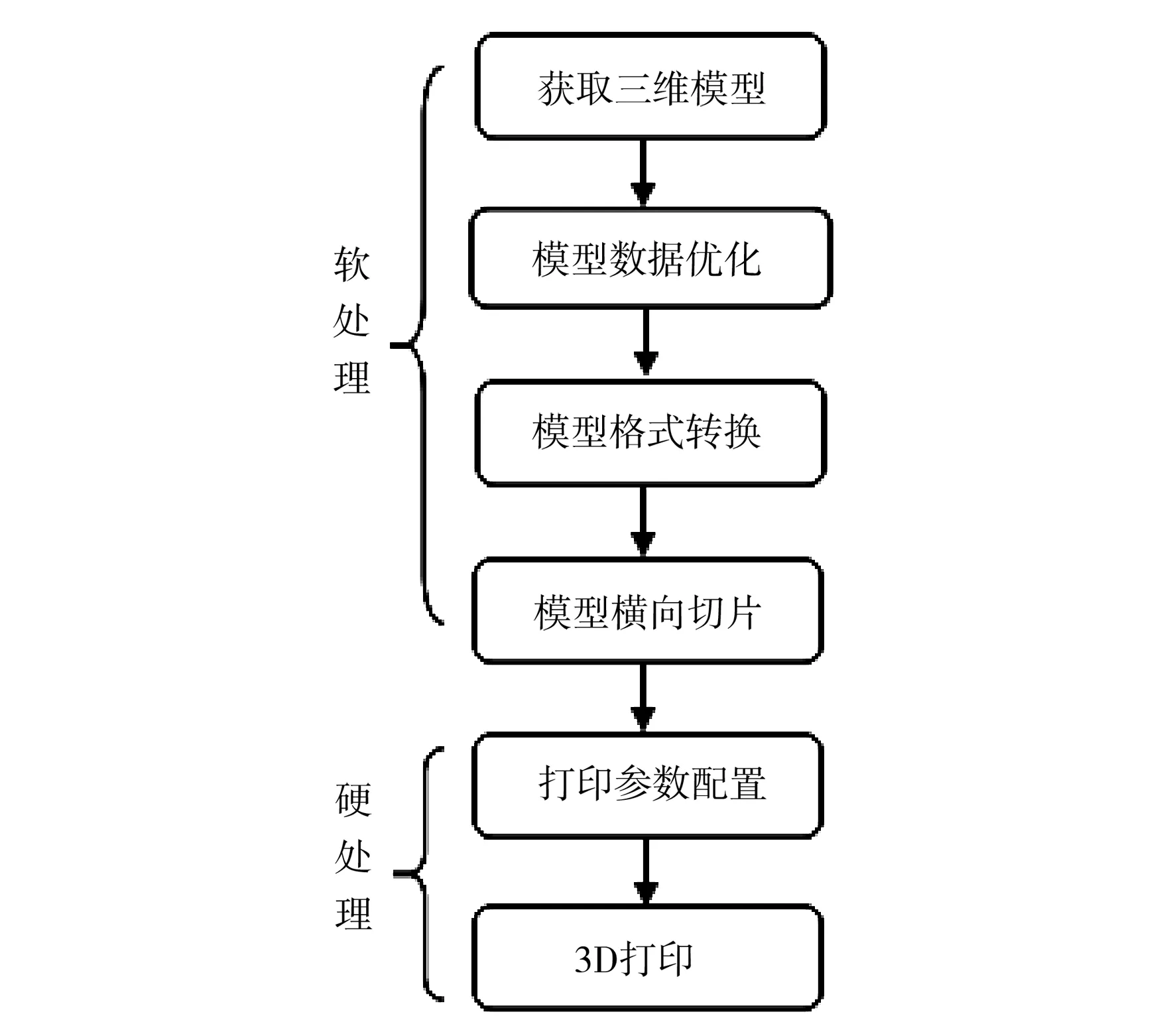
图1 3D打印流程图Fig.1 3D printing flow chart
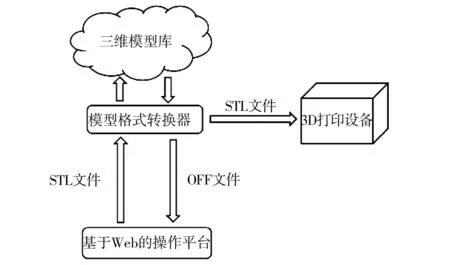
图2 云制造+3D打印Fig.2 Cloud manufacturing + 3D printing
通过以上的大致分析,已经对3D打印流程有了一定的了解,下面本文将对数字处理阶段进行解析。
2 常用模型数据文件格式
模型文件作为3D打印机的基本输入将直接影响到3D打印的效率。对常用模型数据文件格式及文件内部组织结构的分析,有利于更深入的研究模型优化算法,下面将介绍三种常用模型数据文件格式。
2.1 OBJ文件的数据结构
OBJ文件是Alias| Wavefront公司为它的一套3D建模和动画软件“Advanced Visualizer”而开发的3D模型文件格式,该格式以纯文本的形式存储了模型的顶点、面片、法线及纹理坐标等使用信息。这种文件格式由于结构简单,通常是各种模型文件格式转换的中间文件。
2.2 STL文件的数据结构
STL同样也是采用三角形面片进而离散的表示三维模型,STL已成为快速原型技术领域的接口标准。对于STL文件来说,它是由一系列无序的三角面片组成,而三角面片是直接用点来表示的,没有用来反映三角面片之间的拓扑关系,并且每个三角面片都与相邻的三角面片之间共用两个顶点。以部分STL文件片段为例进行分析,分析如下:
solid STL File
Facet normal 0.000000e+000 0.000000e+000 8.729460e+000
outer loop
Vertex 6.198058e-001 2.317201e+001 3.826742e+001
Vertex 6.198058e-001 2.273891e+001 3.826742e+001
Vertex 6.376099e-001 2.318196e+001 3.826742e+001
endloop
endfacet
...
endsolid STL File
片段中以solid关键字开头,指定了文件名,第二行用facet normal关键字指定了指向模型外部的面片法向量,随后以outer loop和endloop为一对关键字描述三角形的三个顶点,endfacet是面片定义结束,endsolid 意味着STL文件的结束。
STL文件的数据结构只能描述三维模型的几何信息,不能表示样式信息,这区别于OBJ文件,STL是计算机图形学、数字几何处理、数字几何工业应用等领域最常用的文件格式,亦是三维打印机支持的最常见文件格式。
2.3 OFF文件的数据结构
利用三角形图元可以近似逼近出几乎所有的三维立体模型,这种逼近方法也是多数三维网格数据文件所采用的方法。OFF( Object Format File )文件也采用了这种方法,它利用点和边组成许多空间三角形来逼近三维模型表面。与其他文件不同,OFF文件的数据只支持ASCII格式存储,利用ASCII格式存储的优点是可读性强,方便理解数据。下面再看一个例子,来理解OFF的数据结构。
OFF
4 4 6
0.0 0.0 2.0
1.632993 -0.942809 -0.666667
0.000000 1.885618 -0.666667
-1.632993 -0.942809 -0.666667
3 1 0 3
3 2 0 1
3 3 0 2
3 3 2 1

图3 OFF文件显示图Fig.3 OFF document display image
如图3所示为该OFF文件的显示图。由示例可知,OFF文件与OBJ文件非常相似,只不过与OFF相比OBJ文件多了一组表示信息,例子中的第二行“4 4 6”,分别代表模型顶点数,三角面片数,边数。随后是顶点坐标及三角面片,拿一个面片为例:“3 1 0 3”中第一个“3”代表随后跟着3个点的索引值,值得注意的是,索引值从0开始( 与OBJ文件不同 )。与STL相似,OFF也没有表示模型样式的相关信息,这很方便进行OFF到STL的转换。
3 一种OFF模型的规范定义
尽管在计算机图形学方面有所建树的国内外学者对三维图形有了深入的研究,但是对于OFF文件数据结构的定义却没有形成一种规范定义。在对OFF模型的数据结构有了一定的了解之后,本小节试图给出OFF描述的三维模型的定义。
3.1 顶点的定义
从集合论的角度很容易得到如下顶点的定义:
V:{p1(x1,y1,z1),…,pn(xn,yn,zn)}
使用C++语言描述的顶点部分定义如下:
Class Vector
{
unsigned int id; /*顶点标识*/
float x,y,z; /*顶点坐标*/
};
3.2 面片的定义
设面片集合:
S:{s1,s2,…,sn}
根据顶点的定义,有映射:
f:V→S
sn=f(pn,pm,pv)
其中pn,pm,pv∈V,sn∈S
得到面片集为:
S:{sn|sn=f(pn,pm,pv),p∈V}
使用C++语言描述的三角面片部分定义如下:
Class Triangle
{
unsigned int id; /*面片标识*/
int verts[3]; /*三角形的三个点的标识*/
int nverts; /*顶点索引个数*/
};
3.3 网格模型的定义
有了上述顶点和面片的定义,很容易完成网格模型的定义。
网格定义如下:
M:{(V,S)}
其中V是包含全部顶点的集合,S是包含由3个V集合上的点所组成的面片集合。
使用C++语言描述的网格模型部分定义如下:
class CMesh
{
Vertex * vertex; /*点集合*/
Triangle * triangle; /*面片集合*/
...
int nVertices,nTriangles,nEdges;
/*存储相关数目*/
public:
void Read();
void RenderScene();
...
};
3.4 网格模型的操作
根据上述模型的定义,可以结合OpenGL编程技术进行模型的读取及绘制操作,OpenGL编程技术的使用能更好的实现三维模型的立体感和真实感,在绘图方面更加有优势。图4为OpenGL显示效果图,可以利用OpenGL提供的各种API接口实现模型的显示。
下面部分代码使用了部分绘图函数:
void CMesh:: RenderScene(){
...
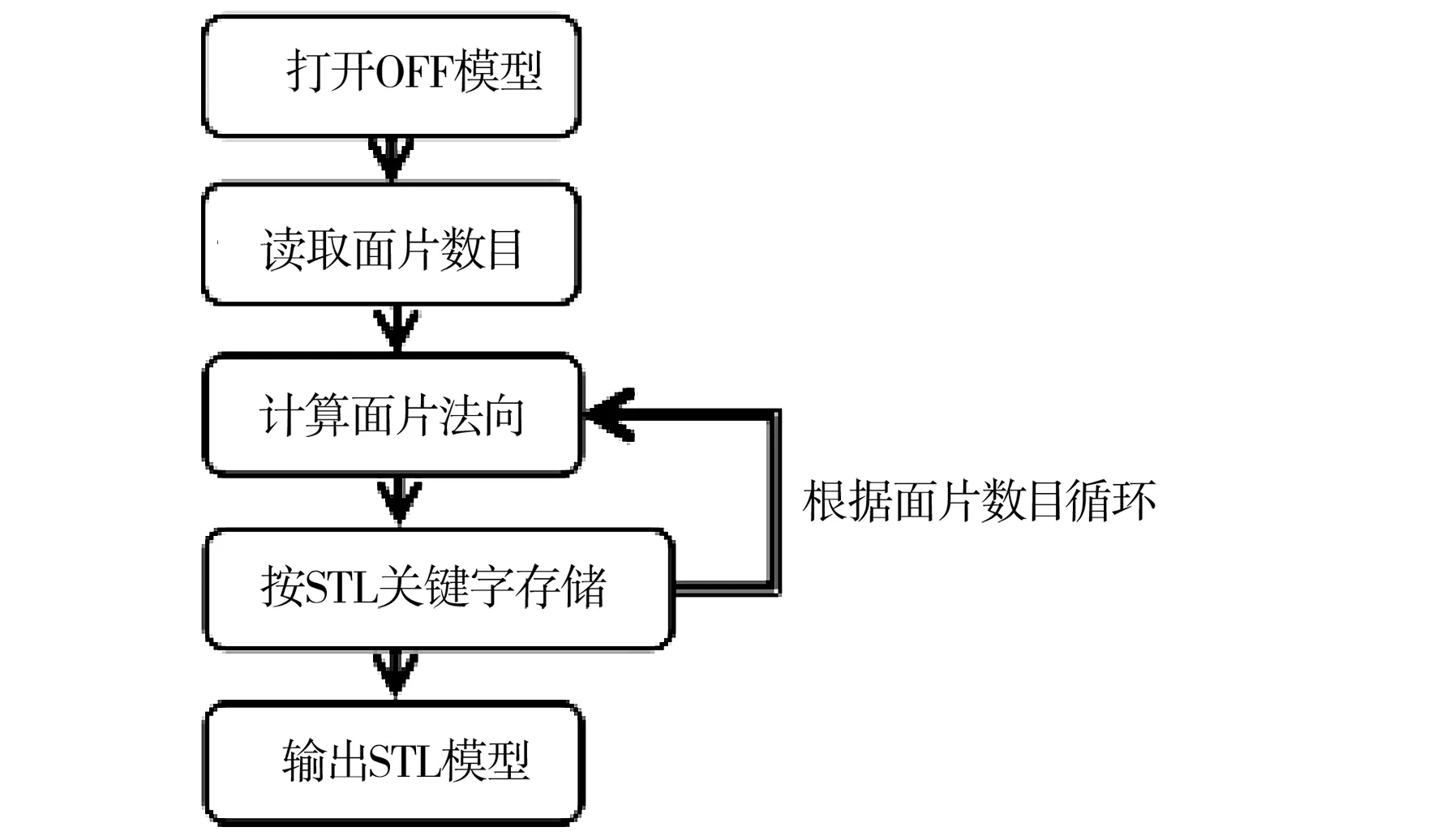
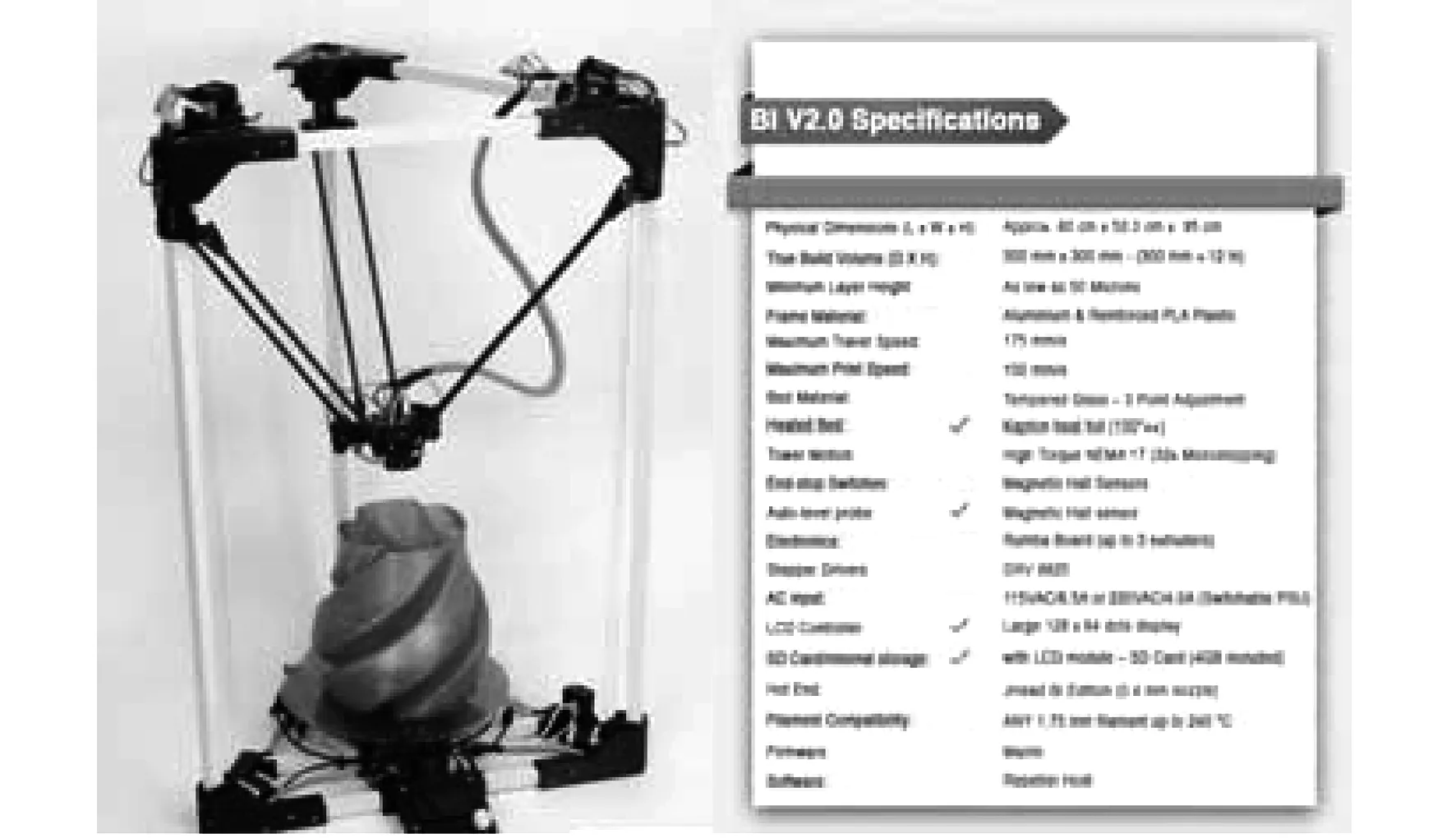
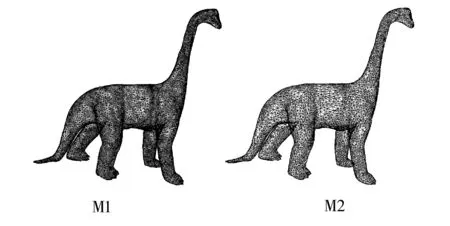
for(int i=0;i glBegin(GL_TRANGLES); glVertex3f(vertex[i].x,vertex[i].y, vertex[i].z); glVertex3f(vertex[i+1].x,vertex[i+1].y, vertex[i+1].z); glVertex3f(vertex[i+2].x,vertex[i+2].y, vertex[i+2].z); glEnd();} ... } 图4 OFF模型显示示例Fig.4 OFF model display scale 3.5 模型互转研究 研究常用三维网格数据文件格式之间的转换,无论对于扩充计算机图形学还是更好地应用3D打印技术来说,都具有非常重要意义。基于上述分析,我们已经对常用模型数据文件格式( OBJ、STL、OFF ) 的内部数据组织结构有了一定了解,下面本文将根据模型的定义分析三种文件的各自特点,提出转换思想。 前面提到的OBJ文件很适合用于模型之间的互转,所以本小节着重分别分析OBJ与STL、OFF的联系和区别。从OBJ文件中可以很容易找到与STL文件、OFF文件的一些联系和区别。 A.OBJ文件可以存储模型的样式等信息,而STL文件与OFF文件并没有相关表示信息,所以在设计转换时只需舍去样式表示信息即可。 B.OBJ文件与OFF文件用索引表示三角面片,但两者表示范围不同,OBJ文件的点索引下标从1开始, OFF文件的点索引下标从0开始。STL用outer loop和endloop关键字结合三个顶点描述三角形面片,所以在设计转换时使用适当的表示方法即可。 C.OBJ文件与STL文件均可存储面片法向量信息,而OFF文件没有相关表示信息。所以在设计转换时,需要计算面片法向量。 D.OFF文件存储了相关点、边及面片的数量信息,而OBJ文件与STL文件没有明确给出,所以在设计转换时需要计算相关信息数目。 通过以上分析可以发现,利用文件的各自特点,通过使用提供的索引信息,使用几何学中的向量法,可求出表示STL文件所用的法向量,进而得到3D打印需要的STL文件格式。 3.6 一种简单的OFF到STL的转换算法 OFF文件和STL文件同样采用二进制文本信息来描述三维模型的方式,但是OFF文件通过其特有的数据结构,较STL文件在数据存储上占有一定的优势,这种优势在建立大型三维模型库、云制造的资源空间等应用上表现得更加明显。因此,可以利用OFF文件存储空间较小这一特点,应用OFF模型文件处理平台对OFF文件进行预处理操作,再通过调用转换算法完成模型转换,来达到节约时间和空间的目的。 图5 转换算法流程Fig.5 Transition algorithm flow path 图5描述了转换算法的流程,下面将实现转换算法代码: Void Transformation algorithm ( CMesh inputMesh/*输入模型文件*/ ) { FILE*fout=fopen(“D://outputMesh.stl”,“w”); //打开输出文件 for(int i = 0; i //遍历表示模型的所有三角形 { Vector vertexA, vertexB, vertexC, tempVector1, tempVector2, normalVector; //结点的获取 vertexA.x=inputMesh.vertex[inputMesh.triangle[i].verts[0]].x; VertexA.y=inputMesh.vertex[inputMesh.triangle[i].verts[0]].y; vertexA.z=inputMesh.vertex[inputMesh.triangle[i].verts[0]].z; /*用第i个三角形的第0个点的索引值来访问第i个三角形的第0个点的坐标值*/ vertexB.x=inputMesh.vertex[inputMesh.triangle[i].verts[1]].x; vertexB.y=inputMesh.vertex[inputMesh.triangle[i].verts[1]].y; vertexB.z=inputMesh.vertex[inputMesh.triangle[i].verts[1]].z; /*用第i个三角形的第1个点的索引值来访问第i个三角形的第1个点的坐标值*/ vertexC.x=inputMesh.vertex[inputMesh.triangle[i].verts[2]].x; vertexC.y=inputMesh.vertex[inputMesh.triangle[i].verts[2]].y; vertexC.z=inputMesh.vertex[inputMesh.triangle[i].verts[2]].z; /*用第i个三角形的第2个点的索引值来访问第i个三角形的第2个点的坐标值*/ //法向量计算区域 tempVector1.x = vertexB.x-vertexA.x; tempVector1.y = vertexB.y-vertexA.y; tempVector1.z = vertexB.z-vertexA.z; tempVector2.x = vertexC.x-vertexA.x; tempVector2.y = vertexC.y-vertexA.y; tempVector2.z = vertexC.z-vertexA.z; normalVector.x=tempVector1.y*tempVector2.z-tempVector1.z*tempVector2.y; normalVector.y=tempVector1.z*tempVector2.x-tempVector1.x*tempVector2.z; normalVector.z=tempVector1.x*tempVector2.y-tempVector1.y*tempVector2.x; //单位化法向量 float mol= sqrt(normalVector.x*normalVector.x+normalVector.y*normalVector.y+normalVector.z*normalVector.z); //向量的模 normalVector.x=normalVector.x/mol; normalVector.y=normalVector.y/mol; normalVector.z=normalVector.z/mol; fwrite();//按照STL格式写入关键字 } fclose(fout);//关闭文件 } 实验步骤:本实验在VC++6.0平台上实现转换算法,并完成若干模型的转换得到3D打印需要的STL文件格式。使用型号为BI V2.0的实验型3D打印机,如图6所示。实验耗材选用ABS树脂,模型使用计算机虚拟合成的三维模型,原始模型如图7中M1所示。实验利用的简化基本操作为边折叠,采用误差测度-二次误差度量算法,并将简化测度化简为计算简单的递推表达式的方法预处理原始模型文件,得到M2所示模型。 图6 BI V2.0 3D打印机Fig.6 BI V2.0 3D printer 利用以上模型,调节切片厚度,填充密度级别并保持其他参数不变的前提下进行打印测试,欲打印模型大小为(W,D,H:100.0 mm,45.07 mm,73.12 mm)。其他主要控制参数见表1。 图7 模型简化Fig.7 Model simplification 表1 其他主要控制参数 新一代信息技术与制造业的融合,正引发影响深远的全球产业革命,更为我国制造业的转型升级、创新发展提供重大机遇,在《中国制造2025》的强国战略下,从“中国制造”到“中国智造”,全面提升产业技术水平和国际竞争力刻不容缓。对于3D打印这一具有跨时代意义的技术而言,大力推动其发展不仅可以促进制造业转型升级,更可为我国科学研究工作贡献强大的力量。 [1] 刘利刚,徐文鹏,王伟明,等.3D打印中的几何计算研究进展[J].计算机学报,2015,(06):1243-1267. [2] 严梽铭,钟艳如.基于VC++和OpenGL的STL文件读取显示[J].计算机系统应用,2009,18(03):172-175. [3] 沙晨明,申作林,申可心.三角网格文件OFF的格式分析及OFF到STL的转化[J].计算机系统应用,2016,(04):232-236. [4] 刘源.三维几何模型的重建与结构优化[D].合肥:中国科学技术大学,2015. [5] 胡瑞珍,黄惠.3D打印启发下的模型实例化优化研究综述[J].计算机辅助设计与图形学学报,2015,(06):961-967. [6] 曾龙,刘永进,张东亮.面向三维打印的特征驱动轮廓线编辑方法[J].计算机辅助设计与图形学学报,2015,(06):974-983. [7] 卫炜,周来水,张丽艳.海量STL文件的快速读取与显示[J].机械科学与技术,2006,25(08):935-938,975. [8] 牛振华,付娅琦,董迁迁. 3D打印速度的研究[J].江苏科技信息,2014,(07):61-62. [9] 王胜法,李宝军,吕掌权,等.面向三维打印的壳状结构汽车及部件模型轻量化建模[J].计算机辅助设计与图形学学报,2015,(06):968-973. [10] 李小丽,马剑雄,李萍,等.3D打印技术及应用趋势[J].自动化仪表,2014,(01):1-5. The geometry of triangular mesh file processing in the application of 3D printing SHEN Zuo-lin, SHA Chen-ming (Harbin University of Science and Technology, Harbin 150040, China) Three dimensional model plays an important part in computer graphics, and the 3D model of mesh description is the precondition of 3D printing application. Understanding of the data structure of triangular mesh file will directly affect the processing of 3D model. Commonly used model data file format is of great significance to the expansion of computer graphics. On the basis of detailed understanding of the 3D printing process, a detailed analysis of the commonly used data structure based on the triangular grid file was made. In view of the problem that the definition of the structure of the OFF model file is not standardized, this paper defines the data structure of the OFF model, presents ideas of a model for transformation, designs a transformation algorithm and designs an experiment to verify the results through 3D printing. Computer graphics; Format conversion; 3D Model; 3D printing; Triangular mesh file 2017-01-06 黑龙江省大学生创新创业训练项目(201510214027) 申作林(1995-),男,本科在读学生。 沙晨明(1981-), 女,硕士,讲师。 TP391.41 A 1674-8646(2017)02-0018-05
4 实验

5 结语
