FVCOM模型关键参数的处理及其在涌潮模拟中的应用

程文龙,潘存鸿*,吴修广

(1. 浙江省水利河口研究院，浙江 杭州 310020；2. 浙江省河口海岸重点实验室，浙江 杭州 310016)

FVCOM模型关键参数的处理及其在涌潮模拟中的应用

程文龙1,2,潘存鸿*1,2,吴修广1,2

(1. 浙江省水利河口研究院，浙江 杭州 310020；2. 浙江省河口海岸重点实验室，浙江 杭州 310016)

通过改进海床阻力系数和设置合适的垂向紊动背景系数，应用FVCOM模型成功再现了钱塘江河口强涌潮的演进过程。海床阻力系数采用Manning公式形式，取值随水深、地形在0.000 2～0.002 9之间变化；垂向紊动背景系数取1×10-4m2/s。模拟结果较好地复演了涌潮到达时刻、涌潮高度及涌潮抬升过程、涌潮水平流速以及其沿垂向分布规律，表明阻力系数及垂向紊动背景系数等关键参数的改进和处理是合理的，可应用于涌潮三维潮流运动特征模拟。

涌潮；FVCOM模型；三维数值模拟；阻力系数；垂向紊动系数

0 引言

潮波传播到大陆架以后，产生非线性畸变，进入河口后，变形更加剧烈。在一定条件下，会形成水位骤然抬升的涨潮潮波前锋线，即为涌潮[1]。涌潮是特殊的浅水间断流运动，流速大、破坏力强、水流特性复杂，对这一问题的数值模拟一直是计算水动力学的难点之一，具有很高的学术价值和实际应用价值。

近10 a来，在涌潮一维和二维大尺度数值模拟方面取得了很大的进展[2-5]，尤其是采用ZHOU et al[6]和HUI et al[7]分别提出的水面梯度法和水位底床法等“和谐”方法后，二维涌潮数值模拟已相当成熟[8]。但是目前涌潮大尺度三维模拟研究较少，SIMON et al[9]采用LES方法对水槽产生的弱涌潮传播进行了三维数值模拟，其尚未应用到实际河口模拟涌潮；王灿星 等[10]采用商用Fluent软件，通过VOF方法处理自由面，对钱塘江弯道水流特征进行了分析；谢东风 等[11]应用FVCOM模型进行了钱塘江河口实际涌潮的三维模拟，再现了涌潮到达时流速及潮位的突变过程，但水平流速的垂向差异不够明显，与实测数据存在一定的差异。本文主要通过改进FVCOM模型的阻力系数，同时选取合适的垂向紊动背景系数，明显改善了钱塘江河口涌潮三维数值模拟结果。

1 FVCOM模型简介及其涌潮模型的建立

1.1 FVCOM模型简介

FVCOM模型原始方程为雷诺平均的三维海洋控制方程组，包含水体连续性方程及动量方程,温度、盐度方程和紊流方程等[12-13]，紊流方程采用修正Mellor-Yamada 2.5阶紊流模型计算，其在σ坐标下形式如下：

(1)

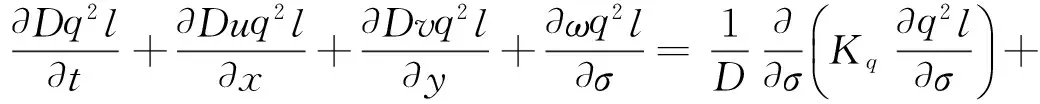
(2)

FVCOM原始方程组可选用半隐方法或者模式分裂求解，半隐方法计算时需要调用PETSC库。模式分裂法中，外模(正压)方程是二维的，基于CFL条件和重力外波波速，时间步长较短；内模(斜压)方程是三维的，基于CFL条件和内波波速，时间步长较长。另外，FVCOM水平方向采用非结构三角形网格，在垂直方向上可采用σ坐标、s坐标和混合坐标系统，同时FVCOM可以较好地处理涨潮和落潮带来的干湿边界转换问题。

1.2 涌潮观测资料

2010年10月9日至17日在钱塘江盐官河段开展了一个完整潮汛期的涌潮水文观测。共布置了3个断面5个水文测点，用ADCP观测流速和流向，另外布置6个潮位站，分别位于3个水文断面的两岸。具体为：盐官断面3个水文测点(左、中、右各1个点)、丁桥(大缺口上游2～3 km)主槽1个水文点和胡斗(老盐仓下游约3～4 km处)主槽1个水文点。水文点位布置如图1所示。流速、流向在涌潮到达后15 min内每隔1 min记录1次，15 min至30 min内每隔2 min记录1次，30 min至60 min内每隔5 min记录1次，其它时间每隔30 min记录1次。同时,涌潮到达后30 min内每隔1 min记录1次潮位，30 min至60 min内每隔5 min记录1次潮位，其余时间每隔15 min记录1次。

1.3 涌潮模型的建立

计算区域上边界取在闸口，下边界为澉浦。该区域包含涌潮形成和涌潮最强的河段(图1)，涌潮特征明显，同时该区域已有不少测量和计算成果可供验证参考。

模型水平方向采用无结构三角形网格对计算域进行剖分，共布置了25 785个单元和13 580个节点，最大步长532 m，网格最小步长56 m，对盐官北岸丁坝等水工建筑物密集区域进行了加密。垂向上采用sigma坐标，共划分20层，按水深均匀分布。压力计算采用静压模式。紊流模型采用FVCOM自带的修正Mellor-Yamada 2.5阶紊流模型。计算采用内、外模分裂模型，因涌潮的强非线性效应，对模型稳定性要求较高，外模时间步长很小，仅为0.1 s，内模时间步长1.0 s。

水下地形资料采用涌潮观测前后同期的实测水下地形，上、下游缺乏同期实测地形的区域采用2010年11月实测水下地形。

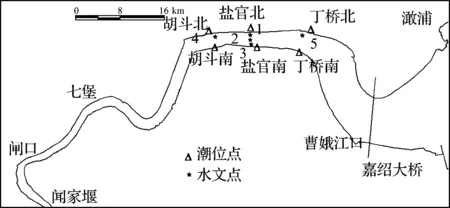
图1 钱塘江河口形势及站位分布图Fig.1 Outline of Qiantang Estuary and distribution of stations

2 FVCOM模型关键参数的改进及其三维涌潮模拟

FVCOM模型本身是一个不断发展的、非常优秀的大洋模型，当应用于钱塘江河口地区时，因该区域水动力过程与大洋相比有很多不同，如：强对流、水浅、河床往往滩槽交互等特征使得其水动力过程复杂多变，特别是涌潮到达时，数秒内，水位骤然上涨2 m左右，高者3 m以上；水流从落潮状态急速转化为涨潮状态，且垂向对流交换剧烈，实测最大垂向流速为0.73 m/s。涌潮过后的数分钟至数十分钟间，流速达到极值，一般水平流速为6～7 m/s。因此，将FVCOM模型应用到钱塘江河口涌潮模拟时，需对能显著影响水动力结果的重要参数进行敏感性分析以确定合适的取值，必要时还需要对这些参数的处理方式进行改进。

2.1 海床阻力系数

FVCOM模型中默认的海床阻力系数计算公式[12-13]为：

(3)

其中：k为卡门常数，zab为最底部水层的厚度。z0为海床粗糙高度，其值的大小主要与床面泥沙的粒径和级配有关，对于床面由均匀沙组成的情况，z0即可取泥沙粒径；对于非均匀沙组成的床面，常选一个较粗的代表粒径(如D90等)作为当量粗糙高度；还可以取更大一些的值，如2.5D90来表征床面起伏后大颗粒突出的影响。一般来说，粗糙高度z0与二维浅水动力学模型常用的Chezy系数C、Manning系数n相比，其物理意义明显，有利于直观地选择其量值[14]。但是该式主要在床面平整、无沙波形态消长、床面阻力以沙粒阻力为主的大洋区域应用较好，而钱塘江强涌潮区域则显著不同，河床滩槽交互，动床阻力主要以沙波阻力为主，而且其阻力系数普遍小于0.002 5，因此采用默认的阻力系数计算公式很难在涌潮计算中得到满意的结果。

本文采用Manning系数来处理河(海)床底部阻力[14]，即将阻力系数一般表达式中的Chezy系数改用Manning系数，采用下式计算：

(4)

式中：n为Manning系数，D为水深，g为重力加速度。

计算中分别采用恒定阻力系数0.002 5和改进后的阻力系数(式4)两种参数进行对比，计算结果显示，尽管模型上、下游边界均为给定实测潮位过程，阻力系数为0.002 5时，与实测值相比，盐官河段沿程低潮位计算值偏高、高潮位计算值偏低，潮差计算值偏小，潮流流速减小也更明显。以盐官1号站为例(图2)，式(3)计算得到的表层流速比式(4)普遍小10%～35%，式(4)结果与实测值吻合更好。另外，汪亚平 等[15]认为在小型潮汐汊道、潮沟、浅水河口、海湾、潟湖中，水深较小，潮流、波浪等动力活跃，整个水层可视为边界层，这也说明采用式(4)总水深计算阻力系数理论上是适宜的。

图2 不同阻力系数下盐官1号站表层水平流速过程对比图Fig.2 The comparison of surface horizontal velocity with different roughness coefficient at Yanguan 1 station

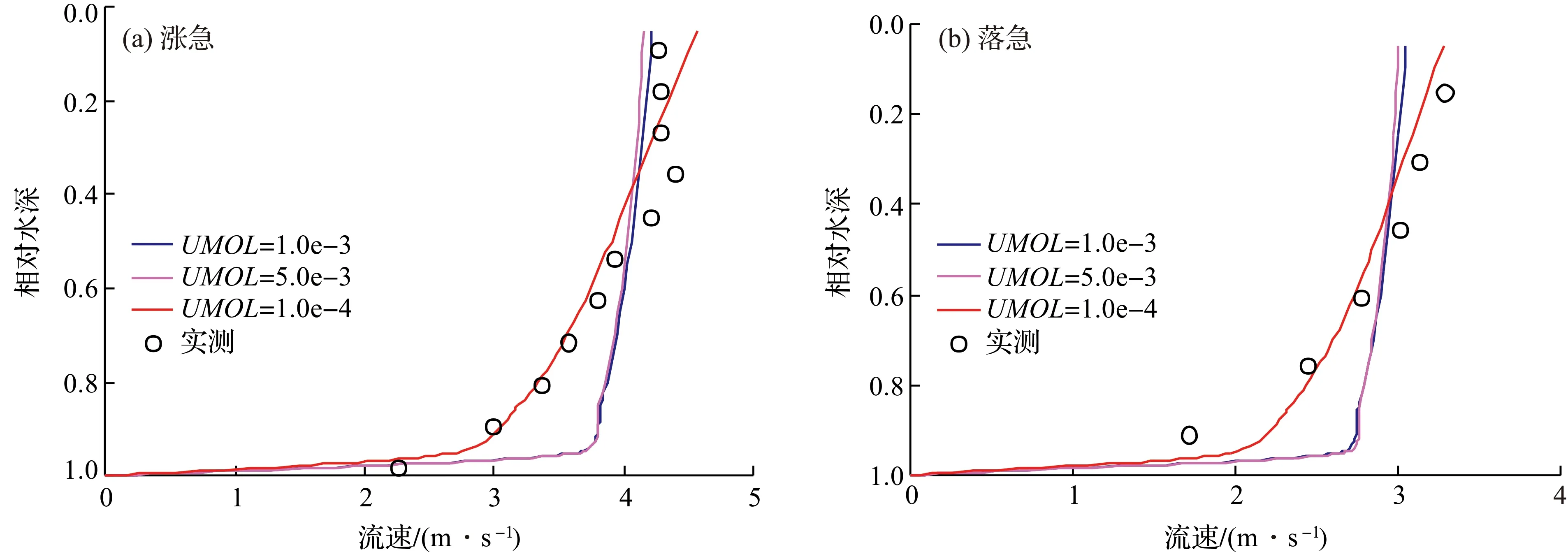
图3 不同垂向背景紊流系数下盐官1号站涨、落急水平流速垂向分布对比图Fig.3 The comparison of vertical distribution of the maximum flood and ebb velocity with different background vertical eddy viscosity at Yanguan 1 station

2.2 垂向紊动系数

垂向紊动系数为二阶项中的系数，其对水平流速的大小和垂向分布影响较大[16]，二阶项对流速的垂向分布起均匀化作用，垂向紊动系数越大，流速垂向分布越均匀，且流速越小。FVCOM湍流模型采用修正Mellor-Yamada 2.5阶紊流模型，其垂向紊流粘性系数Km通过湍流模型计算后再加上垂向背景紊流系数UMOL得到，即Km⟸Km+UMOL，在本研究河段Km值一般为10-4～10-3m2/s。经数值试验，UMOL取较小值(10-5m2/s左右)容易导致计算不稳定，取较大值(10-3m2/s左右)水平流速垂向分布会被匀化，且表层水平流速也减少5%～10%(图3)。因此，涌潮计算中UMOL一般取10-4量级，本文取1×10-4m2/s。

2.3 三维涌潮计算分析

2.3.1 大范围潮位及潮流模拟结果

FVCOM模型通过式(4)计算海床阻力系数，背景垂向紊动系数取1×10-4m2/s，对盐官河段大潮期涌潮开展验证。其中Manning系数取值随河床可动性、滩槽的不同一般为0.006～0.020，与二维浅水动力学模型取值接近[5]，较为简单方便。对应阻力系数Cd值在0.000 2～0.002 9之间变化，其上限比下限大一个数量级，接近式(3)上限，且可以通过调整每个单元的Manning系数值来综合反映河床深槽和边滩的影响。图4为大潮期盐官河段潮位验证图，可见高低潮位值、潮差和相位计算与实测均吻合较好。潮位验证也反映了该河段大潮期涨潮时潮位变化剧烈，涌潮高度自下而上逐渐增大的趋势。

将水平流速模拟结果与实测值按照平均水深、水面以下0.5 m、水面以下1.0 m等至河底以每层层宽0.5 m为间隔绘制成流速、流向过程(图5)，可见流速过程验证吻合较好，特别是结果中各站点垂向上涨急流速、落急流速均能捕捉到，流向过程验证值与实测吻合良好。在空间上，自下而上，盐官河段涨潮最大流速从丁桥至盐官达到最大，到胡斗又开始减小。

2.3.2 涌潮高度及抬升过程模拟结果

将涌潮到达前后，盐官北站潮位过程的模拟结果以每分钟1次的频率输出，与同频率的实测过程进行比较，如图6所示。当涌潮到达时，水位在1 min内抬升接近3 m，再经过几次小幅抬升后达到高潮位，继而开始衰减，潮位逐渐降低。这一潮位过程在模型中被复演，模拟结果在涌潮起涨时间、涌潮高度、小幅抬升以及衰减过程上都较好地吻合了实测值，说明FVCOM模型对流项不作梯度限制处理也能很好地捕捉到涌潮间断过程，仅在涌潮到达后初次抬升幅度(涌潮高度)模拟结果比实测值小约0.8 m，这可能与静压模式中潮头动能转化为势能不充分有关。

图4 潮位验证图Fig.4 Validation diagram of tidal level

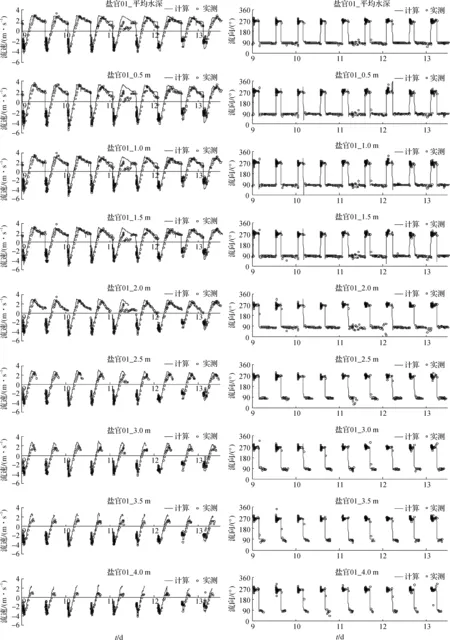
图5 盐官1号站分层流速过程验证图Fig.5 Validation diagram of current in different depth at Yanguan 1 station

图6 涌潮到达前后盐官北潮位过程Fig.6 The tidal level at Yanguanbei before and after tidal bore arrival

图7 涌潮到达前后盐官1号站表层、中层及底层流速、流向过程Fig.7 The surface, middle and bottom velocity magnitude & direction at Yanguan 1 station before and after tidal bore arrival

2.3.3 涌潮过后不同深度流速过程模拟结果

涌潮到达前后盐官1号水文站表层、中层以及底层附近水平流速过程与实测值对比如图7，当涌潮到达时，表层水平流速从落潮1.41 m/s立刻转变为涨潮2.65 m/s，很快涨潮流速回落到2.0 m/s以内，之后流速继续增大，反复一、二次后涨潮流速达到最大，此时离初涨时刻约20 min，模拟潮流结果仍可以复演该过程，且从图中可见，表、中、底层流速均与实测值趋势一致。

总体而言，FVCOM可以较好地模拟涌潮起涨、发展以及消失等整个阶段的潮位和水平方向潮流过程，本次模拟结果较好地反映了本区域涌潮传播的过程，可用于涌潮三维潮流运动特征分析。

3 小结

采用国际、国内广泛应用的FVCOM水动力模型，通过改进海床阻力系数和设置合适的垂向紊动背景系数，在静压假定下，较好地复演了钱塘江河口强涌潮的演进过程，对涌潮到达时刻、涌潮高度、涌潮抬升过程、涌潮水平流速以及其沿垂向分布规律等的模拟结果与实测吻合较好。不过静压假定忽略了水深方向的流动影响，弱化了涌潮潮头“水滚”模拟效果，因此下一步工作拟加强对非静压假定的涌潮的全过程三维数值模拟。

致谢 感谢陈长胜教授领导的SMAST/UMASSD及MEDM研究团队开发、提供FVCOM源代码。

[1] PAN Cun-hong. Numerical simulation for discontinuous shallow water flow and its application to the analysis of the tidal bore at the Qiantang Estuary [D]. Shanghai: Shanghai University,2007.

潘存鸿.浅水间断流动数值模拟及其在钱塘江河口涌潮分析中的应用[D].上海:上海大学,2007.

[2] DU Shan-shan, XUE Lei-ping. Research on one-dimension numerical simulation in tide flow computation[J]. Shanghai Water,2006，22(2):44-47,29.

杜珊珊,薛雷平.长江口北支涌潮的一维数值模拟[J].上海水务，2006，22(2):44-47,29.

[3] YU Pu-bing, PAN Cun-hong. 1D numerical simulation of tidal bore in Qiantang River[J].Chinese Journal of Hydrodynamics,2010，25(5)：669-675.

于普兵，潘存鸿.钱塘江涌潮一维数值模拟[J].水动力学研究与进展:A辑，2010，25(5)：669-675.

[4] PAN C H, LIN B Y, MAO X Z. Case study: Numerical modeling of the tidal bore on the Qiantang River, China [J]. Journal of Hydraulic Engineering,2007,133(2):130-138.

[5] PAN Cun-hong, LU Hai-yan, ZENG Jian. Characteristic and numerical simulation of tidal bore in Qiantang River[J]. Hydro-Science and Engineering,2008(2):1-9.

潘存鸿,鲁海燕,曾剑.钱塘江涌潮特性及其数值模拟[J].水利水运工程学报,2008(2):1-9.

[6] ZHOU J G, CAUSON D M, MINGHAM C G, et al. The surface gradient method for the treatment of source terms in the shallow water equations[J]. Journal of Computational Physics,2001,168(1):1-25.

[7] HUI W H, PAN C H. Water level-bottom topography formulation for the shallow-water flow with application to the tidal bores on the Qiantang river[J]. Computational Fluid Dynamics Journal,2003,12(3):549-554.

[8] PAN Cun-hong. Advances in numerical simulation of discontinuous shallow water flows[J]. Advances in Science and Technology of Water Resources,2010,30(05):77-84.

潘存鸿.浅水间断流动数值模拟研究进展[J].水利水电科技进展,2010,30(05):77-84.

[9] SIMON B, LUBIN P, GLOCKNER S, et al. Three-dimensional numerical simulation of the hydrodynamics generated by a weak breaking tidal bore[C]//Proc. 34th IAHR World Congress, Brisbane, Australia,26 June-1 July,2011:1 133-1 140.

[10] WANG Can-xing, CHEN Ju-fang, JIN Han-hui, et al. Three-dimensional numerical simulation of tidal bore of Qiantang River[J]. Chinese Journal of Hydrodynamics,2012,27(4):367-375.

王灿星，陈菊芳，金晗辉,等.涌潮对钱塘江河道流场影响的三维数值模拟研究[J].水动力学研究与进展:A辑,2012,27(4):367-375.

[11] XIE Dong-feng, PAN Cun-hong, WU Xiu-guang. Three-dimensional numerical modeling of tidal bore in Qiantang based on FVCOM[J]. The Ocean Engineering,2011，29(1)：47-52.

谢东风，潘存鸿，吴修广.基于FVCOM模式的钱塘江河口涌潮三维数值模拟研究[J].海洋工程，2011，29(1)：47-52.

[12] CHEN C S, LIU H D. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries[J]. Journal of Atmospheric and Oceanic Technology,2003,20(01):159-186.

[13] CHEN C S, BEARDSLEY R C, COWLESET G, et al. An unstructured grid, finite-volume community ocean model FVCOM user manual [M].2013.

[14] SHAO Xue-jun, WANG Xing-kui. Introduction to river mechanics[M]. Beijing: Tsinghua University Press,2005:61-62.

邵学军,王兴奎.河流动力学概论[M].北京：清华大学出版社有限公司,2005:61-62.

[15] WANG Ya-ping, GAO Shu, JIA Jian-jun. Flow structure in the marine boundary layer and Bedload Transport: A Review[J]. Marine Geology & Quaternary Geology,2000,20(3):101-106.

汪亚平,高抒，贾建军.海底边界层水流结构及底移质搬运研究进展[J].海洋地质与第四纪地质,2000,20(3):101-106.

[16] CHEN Yong-ping, LIU Jia-ju, YU Guo-hua. A Study on eddy viscosity coefficient in numerical tidal simulation[J]. Journal of Hehai University: Natural Sciences,2002,30(01):39-43.

陈永平,刘家驹,喻国华.潮流数值模拟中紊动粘性系数的研究[J].河海大学学报:自然科学版,2002,30(01):39-43.

Processing on key parameter in FVCOM and its application on tidal bore simulation

CHENG Wen-long1,2, PAN Cun-hong*1,2, WU Xiu-guang1,2

(1.ZhejiangInstituteofHydraulicsandEstuary,Hangzhou310020,China; 2.KeyLaboratoryofEstuaryandCoastofZhejiangProvince,Hangzhou310016,China)

The evolution of tidal bore in Qiantang Estuary were successfully reproduced by applying FVCOM model through improving the sea bed roughness coefficient and setting suitable background vertical eddy viscosity. Sea bed roughness coefficient，calculated using the Manning formulation, is between 0.000 2～0.002 9 with the varying depth. The background vertical eddy viscosity is 1×10-4m2/s. The simulation well reproduces the tidal bore arriving time, tidal level, setup height, horizontal velocity magnitude and vertical profile, which implies the choice of parameters such as the bed roughness coefficient and background vertical eddy viscosity are reasonable. The procedure could be extended to simulate the 3D tidal movement for tidal bores.

tidal bore; FVCOM; 3D mathematic simulation; roughness coefficient; vertical eddy viscosity

10.3969/j.issn.1001-909X.2017.01.004.

2016-02-25

2017-01-05

国家自然科学基金项目资助(51379190)；水利部公益性行业专项项目资助(201001072)；浙江省省属科研院所专项计划项目资助(2016F50018);浙江省科技厅创新团队与人才培养项目资助(2012F20031)；浙江省公益技术应用研究计划项目资助(2016C33095)

程文龙(1981-)，男，湖北公安县人，高级工程师，主要从事河口海岸动力学研究。E-mail:chengwl@zjwater.gov.cn

*通讯作者：潘存鸿(1963-)，男，教授级高级工程师，主要从事河口海岸水动力学、泥沙及水环境研究。E-mail：panch@zjwater.gov.cn

TV131.2

A

1001-909X(2017)01-0033-08

10.3969/j.issn.1001-909X.2017.01.004

程文龙，潘存鸿，吴修广.FVCOM模型关键参数的处理及其在涌潮模拟中的应用[J].海洋学研究,2017,35(1):33-40,

CHENG Wen-long, PAN Cun-hong, WU Xiu-guang. Processing on key parameter in FVCOM and its application on tidal bore simulation[J].Journal of Marine Sciences,2017,35(1):33-40, doi:10.3969/j.issn.1001-909X.2017.01.004.