基于决策树理论的泥石流危险性评价研究*
2017-04-20周仲礼张乾荣曹赛男
周仲礼,张乾荣,,曹赛男
(1.成都理工大学 管理科学学院,四川 成都,610059; 2.成都理工大学 数学地质四川省重点实验室,四川 成都,610059)
基于决策树理论的泥石流危险性评价研究*
周仲礼1,张乾荣1,2,曹赛男2
(1.成都理工大学 管理科学学院,四川 成都,610059; 2.成都理工大学 数学地质四川省重点实验室,四川 成都,610059)
泥石流作为一种破坏性极大的自然灾害,如何科学地评价其影响因子和危险程度显得尤为重要。针对绵竹市清平乡“8.13”特大泥石流灾害,在泥石流危险性评价过程中,采用模糊综合评判法并根据最大隶属度原则确定最后评价结果。然后以评价结果作为决策属性,影响因子作为条件属性,结合粗糙集和决策树理论构建泥石流危险性评价模型。结果表明:影响清平乡泥石流最主要的因素为最大冲出量和剩余固体松散物质,同时通过该模型能快速完成泥石流灾害的危险性评价,评价结果与实际情况吻合,表明将粗糙集和决策树理论用于泥石流危险性评价是切实可行的。
岩土工程;泥石流;评价模型;模糊综合评判法;决策树
我国是一个泥石流频发的国家,根据泥石流爆发程度、分布空间以及时间和类型的不同对人类社会所造成的损失也各不一样。如何确定泥石流的危险程度以及泥石流危险性的影响因素显得尤为重要[1-2]。
对此众多学者对于泥石流评价进行了深入研究,研究对象从单沟评价发展到区域泥石流评价,评价方法也由以往的定性评价方法发展到如今的定量分析评价方法。随着数学理论的快速发展与成熟,不少学者开始将数学方法应用于泥石流危险性评价过程中,比如模糊数学、灰色关联度、层次分析和支持向量机等方法。在信息化时代,计算机技术高速发展,GIS技术开始被学者们广泛地运用于泥石流危险性评价工作中,使得评价内容和结果更加精确与合理。决策树算法是一种对无次序、无规则的训练样本进行推理归纳,从而形成一种特定分类标准的方法。决策树由最经典的ID3算法又衍生出了C4.5和SLIQ等改进算法,研究领域包含了医学、地学以及灾害学等众多学科[3-5]。
笔者试图将粗糙集和决策树理论用于泥石流的危险性评价中,采用模糊综合评判法和决策树算法相结合的思想,并对绵竹市清平乡24条河沟进行实例研究,建立基于决策树理论的泥石流危险性评价模型。
1 泥石流危险性评价模型构建理论
通过查阅泥石流危险性评价相关文献,选择最大冲出量、剩余固体松散物质、流域面积和主沟长度4个影响因子作为泥石流危险性评价指标。首先采用模糊综合评判法进行泥石流危险性评价,再以评价结果作为决策属性,影响因子作为条件属性,结合粗糙集和决策树理论,利用粗糙集求取各属性的上下近似值和近似精度,选择拥有最大近似精度的属性作为决策树的根节点,在此基础之上,对结点的各个属性值进行划分,进而完成决策树模型的构建。
1.1 基于模糊综合评判法的泥石流危险性评价
利用模糊综合评判法进行泥石流危险性评价的基本思路是:确定危险因子论域和评价集,再用灰色关连法确定各危险因子的关联度、权重和隶属度,利用权重和隶属度计算泥石流危险等级模糊集,最后根据最大隶属度原则确定最终评价结果[6-10]
第1步:确定评价集V={V1,V2,V3,V4}={轻度危险,中度危险,高危险,极高危险},危险因子论域U={U1,U2,U3,U4}={最大冲出量,剩余松散固体物源量,流域面积,主沟长度}。
第2步:计算权重。先选择参考序列X0和比较序列X1,进行均值化处理。
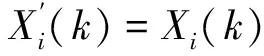
(1)
求绝对差值、最小差和最大差:
(2)
(3)
关联系数:
(4)
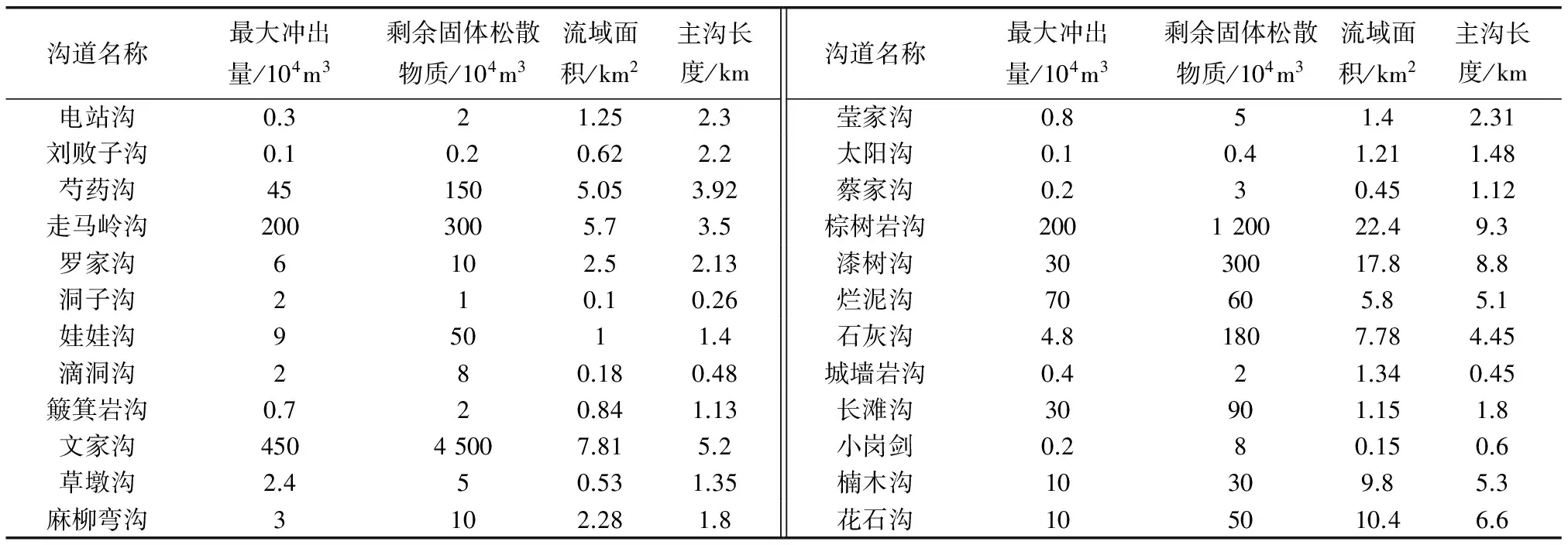
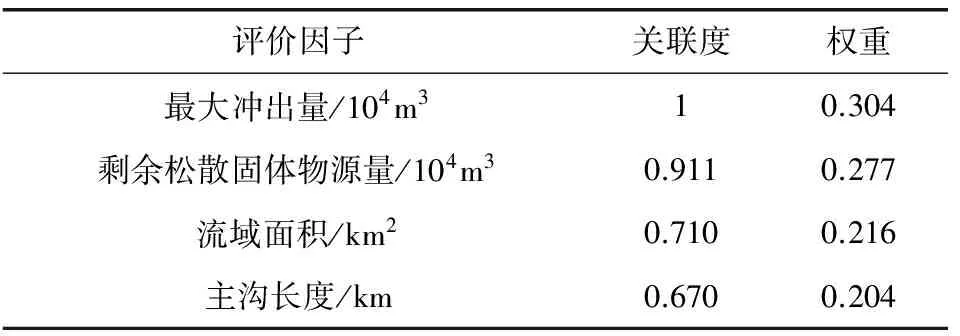
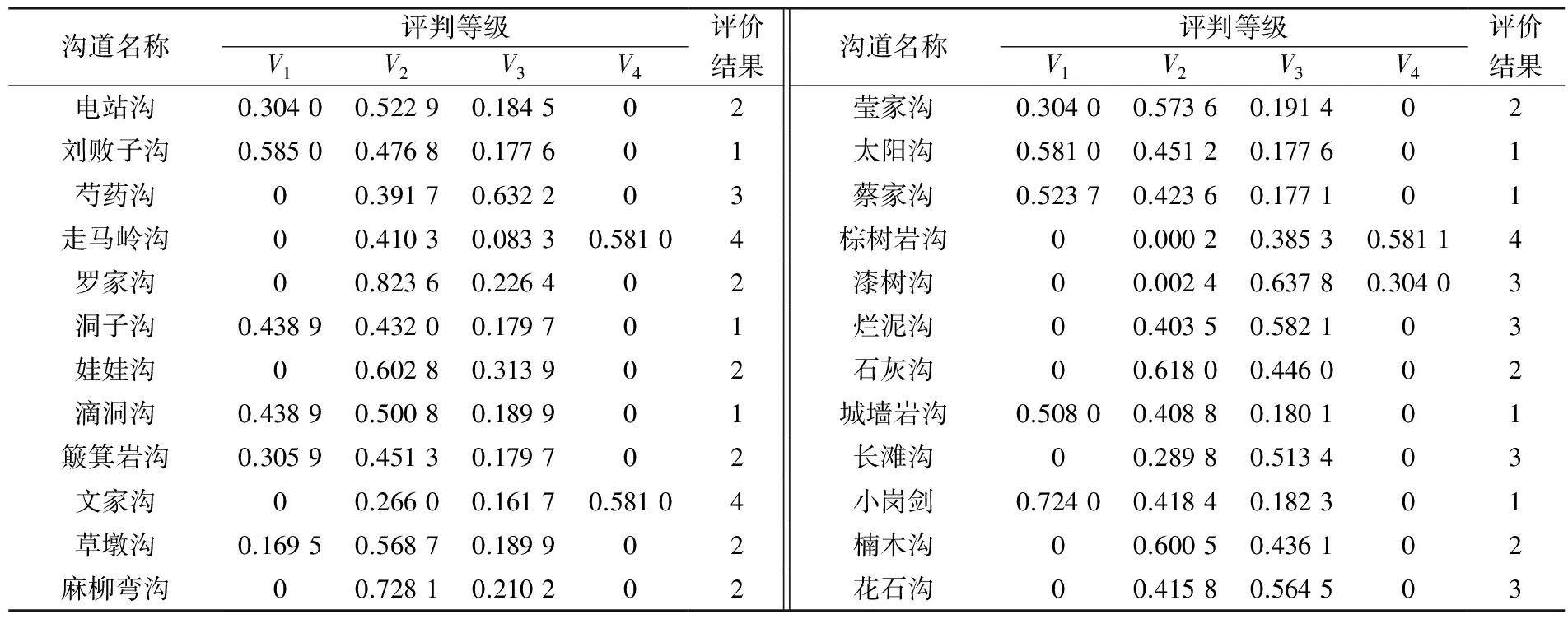
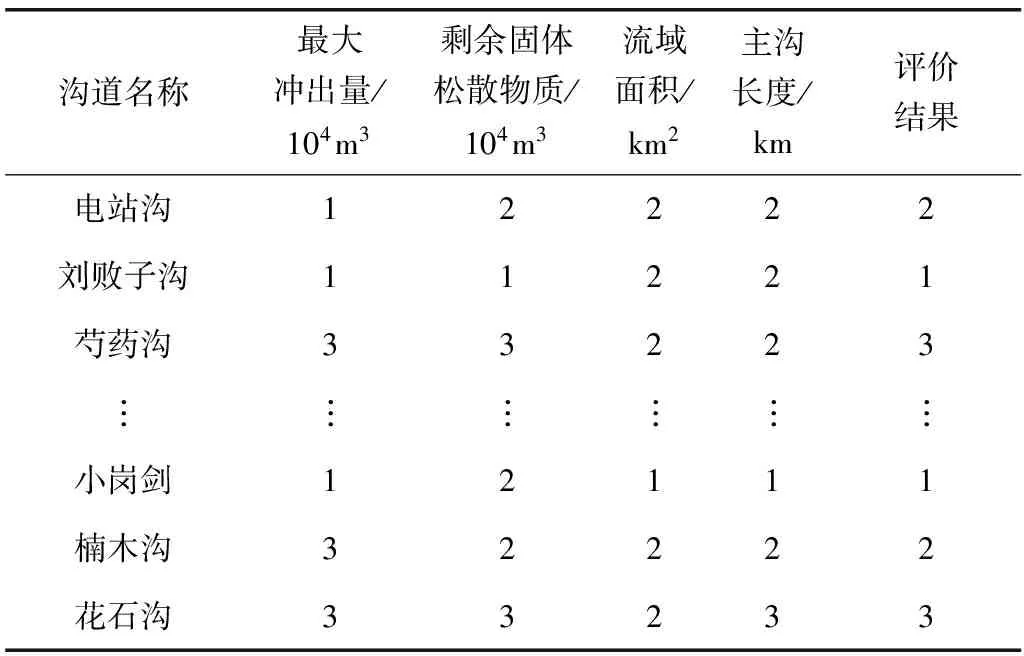
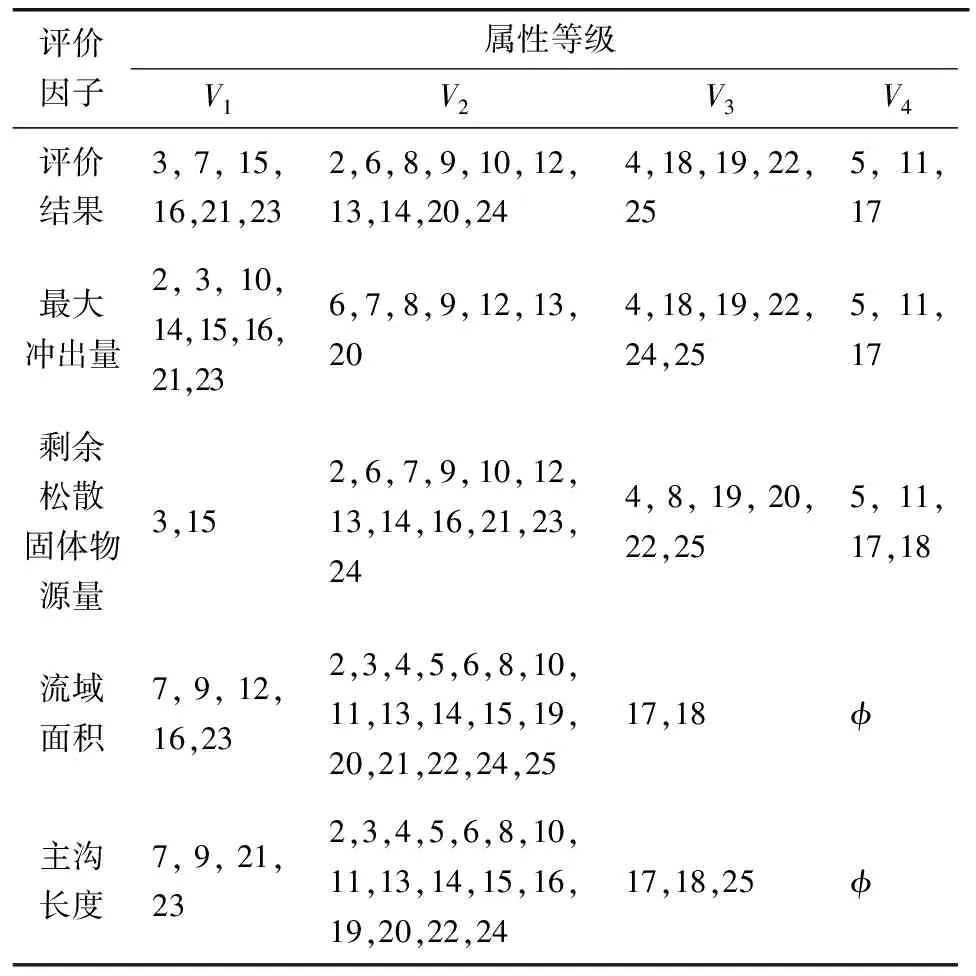
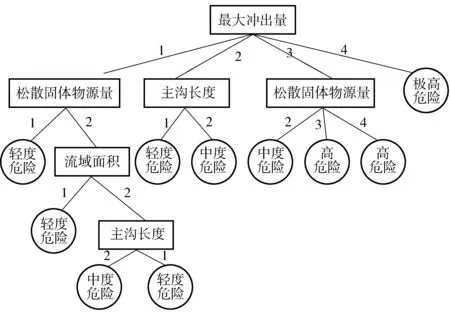
式中:k为常数,0 关联度 (5) 权重 (6) 第3步:引用文献[11]计算隶属度。 隶属度函数: (7) 式中:z为评定因子的实际值;m和c为常数。 (8) 式中:xi和xi+1分别为危险评判标准上下界限。 隶属度矩阵 (9) 第4步:根据模糊向量B和最大隶属度原则确定最终评价等级。 B=W·R (10) 1.2 基于粗糙集的决策树算法 以最终评价结果为决策属性D,危险因子作为条件属性C,建立泥石流的数据信息系统决策表S(U,C∪D)[12-14]。利用粗糙集理论计算各条件属性的上下近似集,进而求得各属性的近似精确度。将根节点选取为拥有最大近似精确度的条件属性,若条件属性的近似精确度相等且不为0,则以属性值类别最少的作为结点,将选为根节点的条件属性的所有属性值进行分支。若属性值的分类结果唯一,该属性值即完成分支。将此类别作为叶节点;若不唯一,则选则除去根节点属性之外的拥有最大近似精确度的条件属性作为下一节点继续分支,直至各个节点中的所有属性值分类唯一。完成决策树构建。其相关定义如下[15-16]: 设论域为U,R是论域上的一个等价关系,X是U的一个子集。则有: (11) (12) 近似精确度 (13) 笔者选取绵竹市清平乡作为研究区,数据来源于文献[18],选择走马岭沟、洞子沟等24条河沟为研究对象。以最大冲出量、剩余固体松散物质、流域面积和主沟长度作为危险因子。数据信息如表1。 表1 清平乡24条沟数据信息 根据绵竹市清平乡泥石流的实际情况和危险程度,将泥石流危险等级划分为轻度危险、中度危险、高危险和极高危险4级,危险性等级量化为1~4级。建立评价集V={V1,V2,V3,V4}={1, 2, 3, 4}。评价标准如表2。 表2 泥石流危险因子评价标准 2.1 泥石流危险性评价 根据泥石流数据信息,选取最大冲出量作为参考序列,其它3个危险因子作为比较序列,将原始数据进行均值化处理,根据式(1)~式(5)计算各危险因子的关联度以及权重,如表3。 表3 各危险因子的关联度和权重 由表3可知权重W={0.304,0.277,0.216,0.204},根据式(7)计算每条泥石流沟道的危险因子对各个危险等级的隶属度和隶属度矩阵。由权重和隶属度矩阵求得各沟道的模糊向量,再依据最大隶属度原则,计算得到24条沟的危险性等级,评价结果如表4。 表4 清平乡泥石流危险性评价结果 2.2 基于粗糙集的泥石流危险性决策树模型构建 以模糊综合评价结果为决策属性,各危险因子作为条件属性,结合各危险因子评价标准(表2)对数据进行离散化处理,构建泥石流离散化数据信息系统S,如表5。 表5 清平乡泥石流离散化数据信息 为求得信息系统中各属性的上下近似,须先求得条件属性和决策属性对于危险等级的分类情况(表6)。 表6 条件属性和决策属性的分类情况 根据表6和式(11)~式(13)求得各属性的上下近似和近似精确度。 aR(剩余固体松散物质)=aR(流域面积)=aR(主沟长度)=0。 从而选取条件属性最大冲出量作为根节点,依据最大冲出量的4个属性值进行划分,当最大冲出量={4}时,决策属性评价结果分类唯一,属于第4级,即极高危险;当最大冲出量={3}时,条件属性剩余固体松散物质分类唯一,从而选取属性剩余固体松散物质为下一节点。最大冲出量={3},剩余固体松散物质={2}时,决策属性为第2级(中度危险),最大冲出量={3},剩余固体松散物质={3,4}时,决策属性为第3级(高危险)。按此方法进行逐步分支,直到所有属性的结果分类唯一。完成泥石流危险性决策树模型构建(图1)。 图1 泥石流危险性决策树模型示意Fig. 1 Decision tree model of debris flow risk 笔者通过分析泥石流危险性评价研究现状,探索性地将粗糙集理论和决策树理论用于泥石流危险性评价中。在模糊综合评价基础之上,就泥石流危险因素进行分析,进而利用粗糙集理论和决策树理论,构建泥石流危险性评价模型。从构建的决策树模型可以判断出最大冲出量和剩余固体松散物质是影响泥石流危险性最主要的因素,使得评价过程更加简洁明了。 通过实例分析可以看出,当最大冲出量大于100×104m3时,泥石流危险性等级为第4级,即极高危险;当最大冲出量大于2×104m3且小于9×104m3时,并且剩余固体松散物质大于0.6×104m3且小于50×104m3时,泥石流的危险性等级为第2级,即中度危险。从利用决策树模型得到的评价结果来看,与实际情况吻合,评价更加高效。 [1] 唐邦兴,杜荣桓,康志成,等.我国泥石流研究[J].地理学报,1980,35(3):259-264. TANG Bangxing, DU Ronghuan, KANG Zhicheng, et al. Study on debris flow in China[J].ACTAGeographicaSinica, 1980, 35(3):259-264. [2] 张梁,张业成,罗元华.地质灾害灾情评估理论与实践[M].北京:地质出版社,1998. ZHANG Liang, ZHANG Yecheng, LUO Yuanhua.TheoryandPracticeofGeologicalDisasterAssessment[M]. Beijing:Geological Publishing House, 1998. [3] MONTALDO N, ALBERTSON J D. Multi-scale assimilation of surface soil moisture data for robust root zone moisture predictions[J].AdvanceinWaterResources, 2003, 26(1):33-44. [4] 苗夺谦,王珏.基于粗糙集的多变量决策树的构造方法[J].软件学报,1997,8(6):425-431. MIAO Duoqian, WANG Jue. Rough sets based approach for multivariate decision tree construction[J].JournalofSoftware, 1997, 8(6):425-431. [5] 罗秋瑾,陈世联.基于值约简和决策树的最简规则提取算法[J].计算机应用,2005,25(8):1853-1855. LUO Qiujin, CHEN Shilian. Algorithm based on value reduction and decision tree to generate minimal rules[J].ComputerApplications, 2005, 25(8):1853-1855. [6] 刘丽,张士革.滑坡、泥石流区域危险度二级模糊综合评判初探[J].自然灾害学报,1996,5(3):51-59. LIU Li, ZHANG Shige. Preliminary research of two-level fuzzy comprehensive evaluation on landslide and debris flow risk degree of a district[J].JournalofNaturalDisasters, 1996, 5(3):51-59. [7] 张跃,邹寿平,宿芳.模糊数学方法及应用[M].北京:煤炭工业出版社,1992. ZHANG Yue, ZOU Shouping, SU Fang.FuzzyMathematicsMethodandItsApplication[M]. Beijing:China Coal Industry Publishing House, 1992. [8] HEATHMAN G C,STARKS P J, AHUJA L R, et al. Assimilation of surface soil moisture to estimate profile soil water content[J].JournalofHydrology, 2003, 279(1/4):1-17. [9] 谷秀芝,陈洪凯,刘厚成.泥石流危险性SIGA-BP神经网络评价方法及应用[J].重庆交通大学学报(自然科学版),2010,29(1):98-102. GU Xiuzhi, CHEN Hongkai, LIU Houcheng. Method and application of debris flow hazard assessment based on SIGA-BP neural network[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2010, 29(1):98-102. [10] 王子健,肖盛燮,戴廷利,等.泥石流危险度模糊综合评判方法及应用[J].重庆交通大学学报(自然科学版),2008,27(5):794-798. WANG Zijian, XIAO Shengxie, DAI Tingli, et al.Fuzzy comprehensive evaluation method and its application in judging the risk degree of debris flows[J].ChongqingJiaotongUniversity(NaturalScience), 2008, 27(5):794-798. [11] 苏经宇,周锡元,樊水荣.泥石流危险等级评价的模糊数学方法[J].自然灾害学报,1993,2(2):83-91. SU Jingyu, ZHOU Xiyuan, FAN Shuirong. A fuzzy set evaluation method of hazard degree of debris flow[J].JournalofNaturalDisasters, 1993, 2(2):83-91. [12] PAWLAK Z. Rough set theory and its applications to data analysis[J].Cybernetics&SystemsanInternationalJournal, 2010, 29(29):661-668. [13] 王国胤.Rough 集理论与知识获取[M].西安:西安交通大学出版社,2001. WANG Guoyin.RoughSetTheoryandKnowledgeAcquisition[M]. Xi’an:Xi’an Jiaotong University Press, 2001. [14] 赵卫东,盛昭瀚,何建敏.粗糙集在决策树生成中的应用[J].东南大学学报(自然科学版),2000,30(4):132-137. ZHAO Weidong, SHENG Zhaohan, HE Jianmin. Application of rough sets to the designing of decision trees[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2000, 30(4):132-137. [15] QUINLAN J R. Induction of decision trees[J].MachineLearning, 1986, 1(1):81-106. [16] 邹瑞芝,罗可,曾正良.基于粗糙集理论的决策树分类方法[J].计算机工程与科学,2009,31(10):112-115. ZOU Ruizhi, LUO Ke, ZENG Zhengliang. A classification method using decision trees based on rough sets[J].ComputerEngineering&Science, 2009, 31(10):112-115. [17] 向红艳,金明.基于多变量决策树交通事件持续时间预测模型[J].重庆交通大学学报(自然科学版),2015,34(3):112-116. XIANG Hongyan, JIN Ming. A traffic incident duration time prediction model using multivariable decision tree[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2015, 34(3):112-116. [18] 苏鹏程,韦方强,冯汉中,等.“8.13”四川清平群发性泥石流灾害成因及其影响[J].山地学报,2011,29(3):337-347. SU Pengcheng, WEI Fangqiang, FENG Hanzhong, et al. Causes and effects of group-occurring debris flow disasters in Qingping town, Mianyang river upstream, Sichuan[J].JournalofMountainScience, 2011, 29(3):337-347. (责任编辑:刘 韬) Risk Assessment of Debris Flow Based on Decision Tree Theory ZHOU Zhongli1, ZHANG Qianrong1, 2, CAO Sainan2 (1. School of Management Science, Chengdu University of Technology, Chengdu 610059, Sichuan, P. R. China; 2. Key Laboratory of Mathematical Geologyof Sichuan Province, Chengdu University of Technology, Chengdu 610059, Sichuan, P. R. China) Debris flow is a kind of destructive natural disasters, and how to scientifically evaluate its influence factor and risk degree is very important. Aiming at “8.13” catastrophic debris flow at Qingping township in Mianzhu, the fuzzy comprehensive evaluation method and the maximum membership principle were used to determine the final evaluation results in the process of debris flow risk assessment. And then, taking evaluation results as decision attributes and impact factors as condition attributes, the debris flow risk assessment model was established, combined with rough set and decision tree theory. The results show that the main factors affecting the debris flow in Qingping township are the largest output of the debris flow and the residual solid loose material. At the same time, the risk assessment of debris flow can be completed quickly through the proposed model and the evaluation results are in agreement with the actual situation, which shows that using rough set and decision tree theory to evaluate the risk of debris flow is feasible. geotechnical engineering; debris flow; evaluation model; fuzzy comprehensive evaluation method; decision tree 10.3969/j.issn.1674-0696.2017.04.13 2015-10-14; 2016-04-15 四川省教育厅自然科学重大培育项目(14CZ0007) 周仲礼(1971—),男,四川成都人,教授,博士,主要从事数学地质方面的研究。E-mail:380990486@qq.com。 张乾荣(1991—),男,四川南充人,硕士研究生,主要从事数学地质方面的研究。E-mail:13551352053@163.com。 P642.23 A 1674-0696(2017)04-076-05
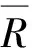
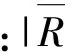
2 实例应用

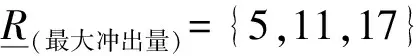
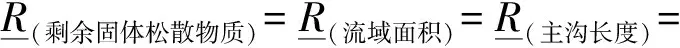
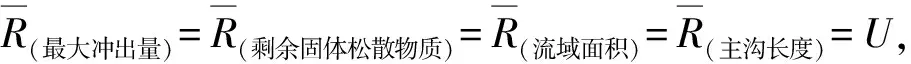
3 结 语
