横梁效应对车-桥耦合振动的影响研究*

王 帆，吴红林

(1.林同棪国际工程咨询(中国)有限公司，重庆 401121；2.哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 150090)

横梁效应对车-桥耦合振动的影响研究*

王 帆1，吴红林2

(1.林同棪国际工程咨询(中国)有限公司，重庆 401121；2.哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 150090)

提出了由横梁效应引起的附加不平整度的简化计算模型，给出了考虑横梁效应的车-桥耦合振动问题求解方法，解决了模态综合法因采用截断模态无法反映桥梁结构如横梁、桥面板等局部构件振动情况的问题，并通过算例对横梁效应考虑与否进行了对比分析，同时引入描述横梁效应桥面系刚度变化幅度的无量纲参数γ，研究了其对考虑车-桥耦合振动的影响。研究结果表明：横梁效应与车-桥振动系统存在耦合关系，其效应值随参数γ增加而增加，呈高次变化规律。

桥梁工程；车-桥耦合振动；横梁效应；附加不平整度；模态综合法；弹性支承刚度

0 引 言

近一个世纪以来，国内外学者对桥梁在车辆移动荷载作用下的车桥耦合振动问题进行了大量研究工作[1-2]。大量事实表明，即使车-桥系统不受任何外力作用，系统仍然会发生强烈的振动，这是因为车-桥耦合系统存在桥面不平整度等内部激扰因素，使得车-桥耦合系统具有自激性[3]。为保证车桥耦合振动分析的准确性，则需考虑桥面平整度的影响。目前不平整度对车桥耦合振动响应的影响研究均是针对路面铺装不平整状况开展的，采用功率谱密度函数模拟桥面不平整度序列[4-5]。

由于桥面板支撑刚度沿长度方向是不断变化的，导致车辆在行驶过程中使得桥面的竖向挠度不断变化，形成了附加不平整度。作为一种内部激扰因素影响车-桥耦合系统振动响应，即为横梁效应[6]。笔者对其进行了分析，提出了考虑横梁效应的车-桥耦合振动求解方法，并研究了横梁效应的影响参数。

1 车-桥系统耦合振动方程

1.1 桥梁振动模型

桥梁结构振动是多自由度体系的复杂振动问题，一般可采用模态综合法，把桥梁相互耦合的各个自由度振动方程转化为一组具有相同自由度的非耦合的振动方程，用解耦后的模态信息描述桥梁结构的振动，以减少自由度数量，提高计算效率。桥梁振动方程为

(1)

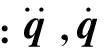
1.2 车辆振动模型

车辆的振动同样是多自由度的振动问题，但考虑到车辆竖向和横向振动之间仅存在弱耦合作用，且横向振动相对竖向振动很小，通常采用7自由度模型描述车辆的振动。

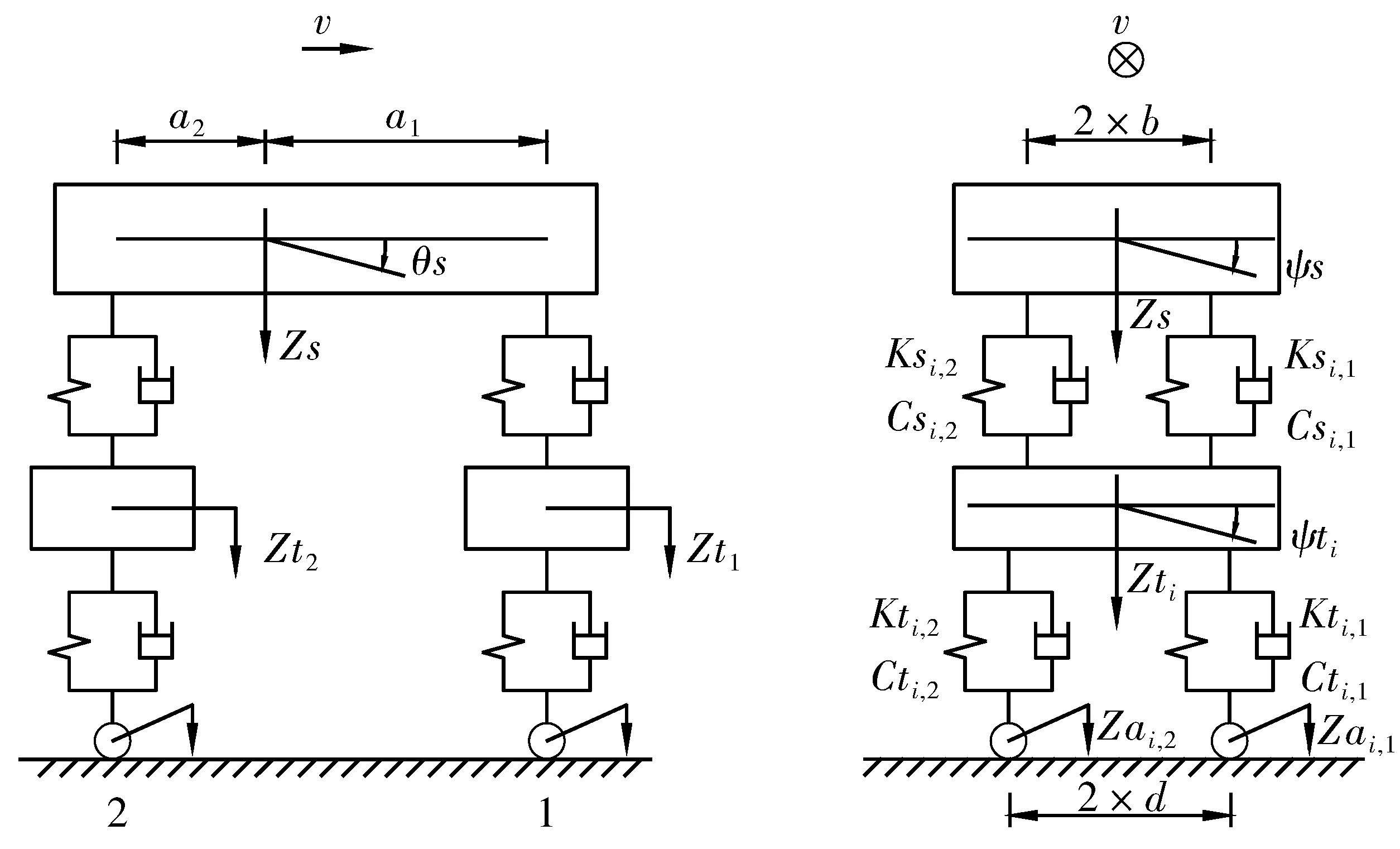
图1 车辆模型Fig. 1 Vehicle model

通过达朗贝尔原理、拉格朗日方程或刚度集装等方法，可以得到车辆子系统的动力学方程为

(2)

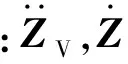
1.3 耦合关系

上述桥梁和车辆振动模型通过接触点耦合关系联系起来，车-桥耦合振动动力响应求解的关键在于接触点耦合关系的确定。车-桥系统的耦合关系主要是接触点的位移协调关系和耦合作用力平衡关系[7]。

接触点耦合自由度的位移za包括桥梁接触点的竖向挠度z(x,t)=∑ψiqi和路面不平整度值r，即为

(3)

耦合作用力是一对相互作用力，但两者并不是相等的，其作用值与车辆振动状态、桥梁振动状态、车辆位置、桥面不平整度、行车速度都有关。桥梁对车辆的作用力为

(4)

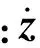
车辆作用在桥梁上的力为

(5)

式中：G为车辆重量；C′，K′分别为耦合系数矩阵。

2 横梁效应

对于典型纵横梁体系的桥面系而言，由于横梁和桥面板在车辆荷载作用下均存在竖向变形，而且变形量随桥面位置的不同而不同，桥面系呈现出不同的支承刚度，如图2。

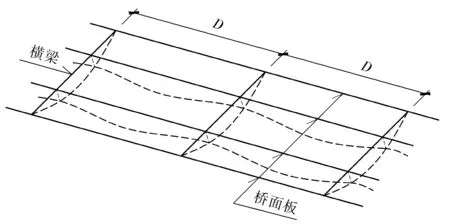
图2 桥面板变形示意Fig. 2 Schematic of deck deformation

而模态综合法求解车-桥系统耦合振动响应时一般采用截断模态，即采用较少的低阶模态便可较好地反应桥梁振动情况[8]，但对于桥梁结构，低阶模态一般为结构整体面内、面外或扭转模态，不能反应上述横梁、桥面板等局部变形引起的振动情况。因此，为更精确地计算车桥耦合振动动力响应，应将横梁及桥面板的竖向变形作为附加不平整度，计入车-桥系统接触点耦合自由度中。

显然，这种附加不平整度由横梁变形和桥面板变形两部分组成，如图3。

接触点竖向挠度即附加不平整度Δ为

Δ=(1-λ)Δhi+λΔhj+Δb

(6)

式中：λ=x/D为车辆相对位置，D为横梁间距；Δhi，Δhj分别为横梁i，j的竖向变形；Δb为桥面板竖向变形。

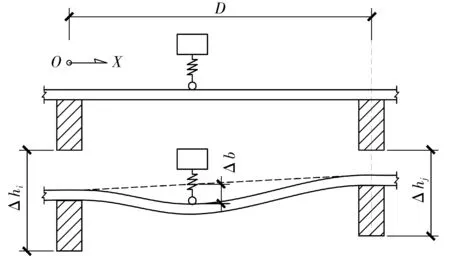
图3 附加不平整度计算示意Fig. 3 Additional roughness computation

假设横梁刚度均为弹性支承刚度即k0，桥面板截面刚度为EI，单位力作用下两横梁间接触点任意位置竖向挠度Δ(λ)可以通过结构力学求得

(7)

桥面系刚度k(λ)为

(8)

上述桥面系刚度k(λ)解析式十分复杂，且受控于横梁弹性支承刚度k0，而k0因结构体系、横梁位置、横梁截面抗弯刚度的不同而不同,难以得到解析式。考虑到系数λ2+(1-λ)2和λ2(1-λ)2在λ∈[0,1]范围内均与余弦函数形状类似，且一般桥梁结构横梁间距远小于桥梁跨度，每两个横梁之间呈现出相同的弹性刚度变化规律，因此，用余弦函数来近似模拟全桥桥面系刚度是十分合适的。将桥面系等效成变刚度弹性层，则

k(x)=k1+k2cos2πx/D

(9)

式中：k1=(kmax+kmin)/2;k2=(kmax-kmin)/2。

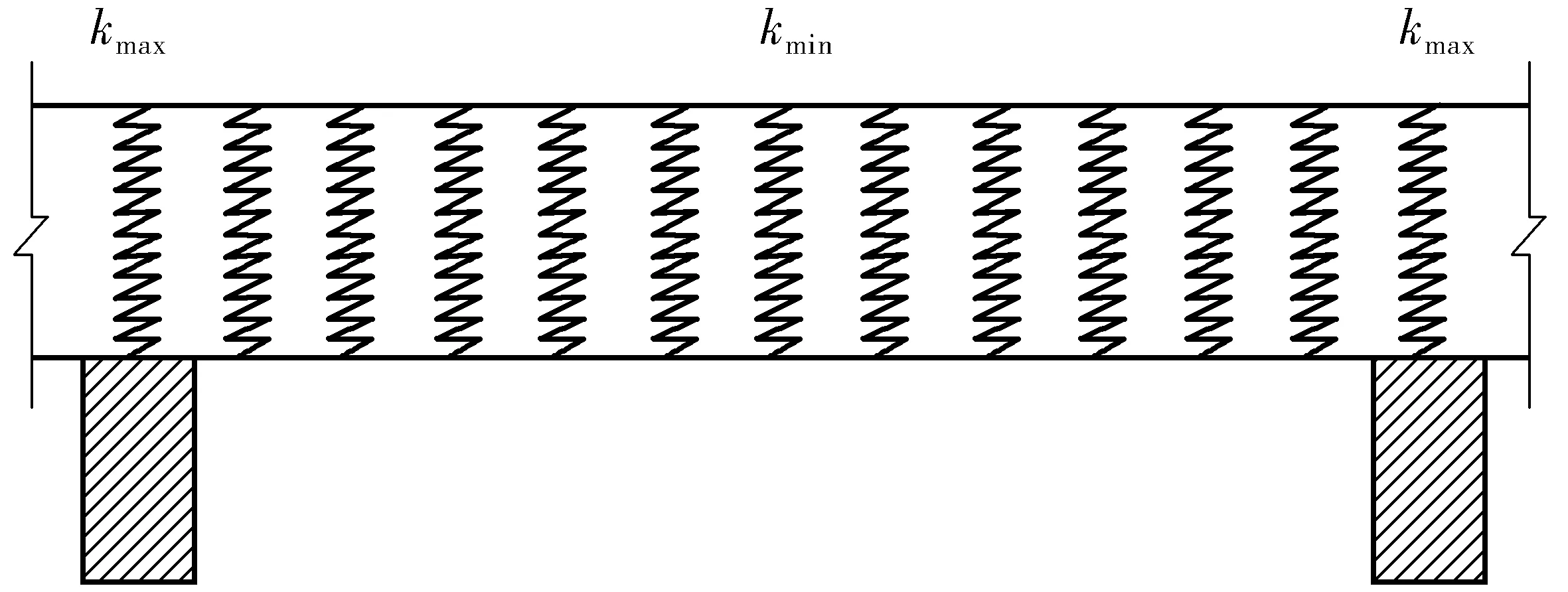
图4 等效弹性层Fig. 4 Equivalent elastic layer

显然，当车辆行驶在横梁上时支承刚度最大，行驶在两横梁跨度中间时支承刚度最小，可通过有限元分析软件求解对应的等效刚度kmax和kmin，如图5(a)，板跨中作用单位荷载时作用点静挠度为δmin，如图5(b)，横梁中心作用单位荷载时作用点静挠度为δmax,则kmax=1/δmin，kmin=1/δmax。

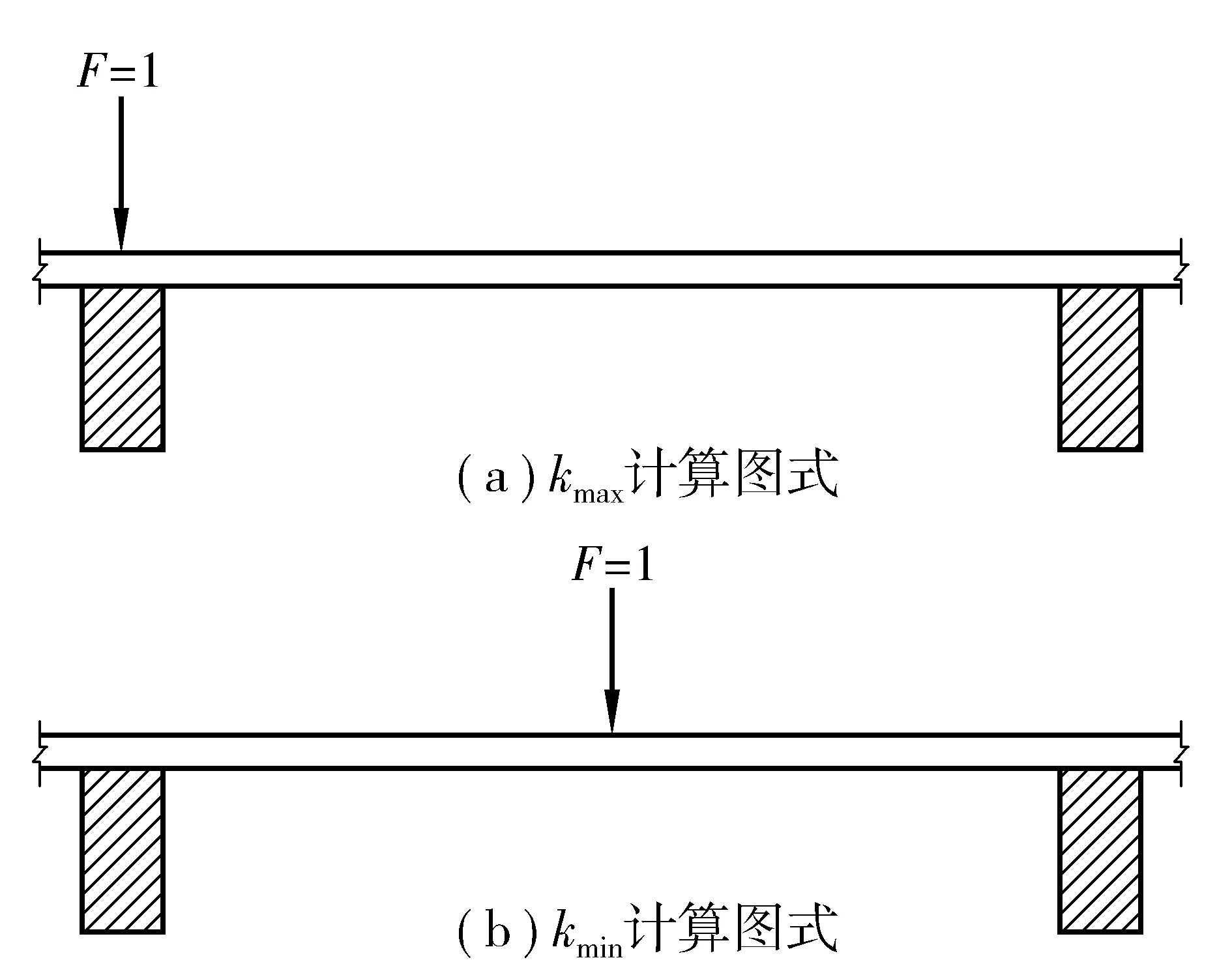
图5 等效刚度计算示意Fig. 5 Calculation diagram of equivalent stiffness

那么，桥面板由于横梁效应引起的附加不平整度即为

(10)

可以看出，横梁效应引起的附加不平整度与路面随机不平整度不同的是，它与车桥系统存在耦合关系，附加不平整度值除了与桥面系等效支承刚度有关，同时还受车桥系统振动本身的影响。

将上述横梁效应引起的附加不平整度Δ迭加到接触点耦合自由度中：

(11)

将其代入车-桥系统耦合振动方程中进行分离迭代求解，即为考虑横梁效应后的车-桥耦合振动动力响应。

3 算 例

跨度为20 m的简支板梁桥，双纵梁之间间距为8 m，全桥每5 m设置共5道横隔梁，纵梁与横梁均为C50混凝土0.5 m×1.6 m矩形实心截面，桥面板为20 cm厚C50钢筋混凝土板，如图6。车辆采用文献[9]的计算模型，车体质量为57 500 kg，车体弹簧刚度为1 595 kN/m，行车速度为20 m/s，车辆沿桥梁中心线行驶。图7为桥面跨中A点的动力响应时程曲线。由图7可以看出，横梁效应对车桥耦合振动分析有较为显著的影响，不考虑横梁效应时跨中截面最大竖向挠度为8.4 mm，而考虑横梁效应后，最大竖向挠度达到了9.2 mm，增加了9.5%。

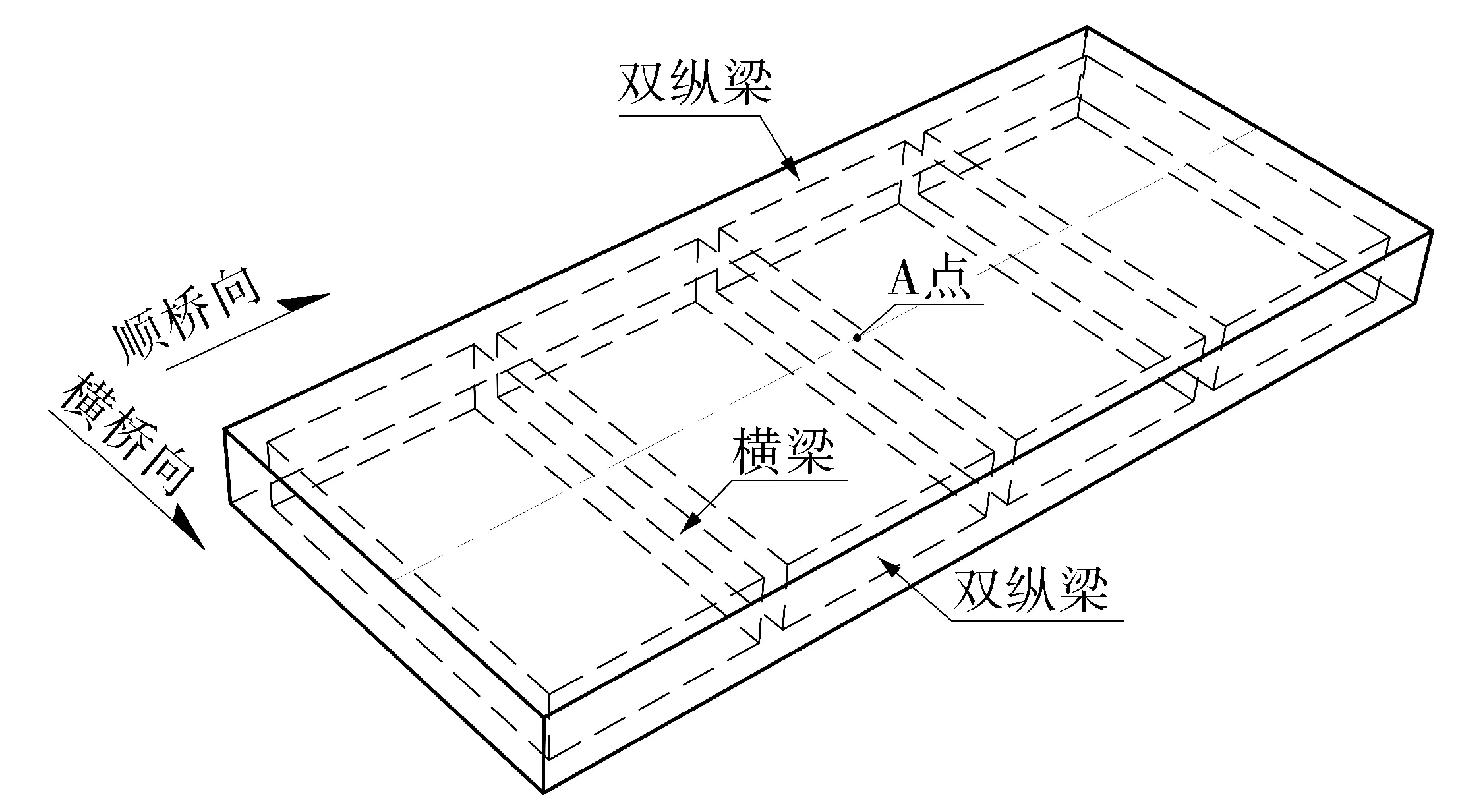
图6 结构示意Fig. 6 Structure

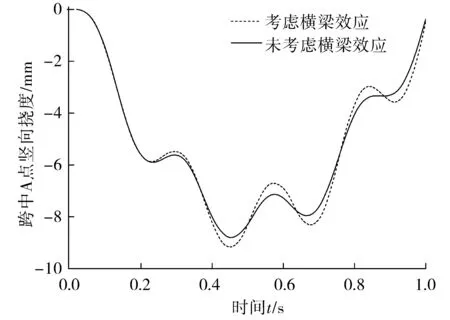
图7 跨中挠度时程曲线Fig. 7 Time-history curve of the middle span deflection

4 横梁效应影响参数分析

横梁效应是因为桥面板支撑刚度的变化所引起的，显然其效应与刚度变化的幅度有直接关系。引入无量纲参数γ：

(12)

考虑和不考虑横梁效应的车桥耦合振动动挠度影响参数η：

改变前文数值实验模型中桥面板厚，分别取35，30，25，20，15 cm，使得参数γ在0.53～0.90范围内变化，影响参数η随刚度比参数γ的变化规律如图8。

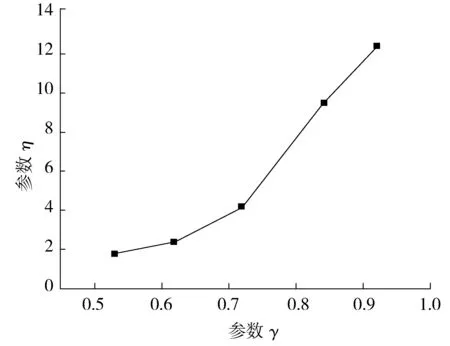
图8 参数γ的影响规律Fig. 8 Influence law of parameter γ

由图8可以看出，横梁效应随刚度比γ的增大而增大，呈高次变化趋势；当γ<0.6时横梁效应影响参数η<2，此时横梁效应并不明显，此时计算车-桥系统耦合振动时可不计入横梁效应引起的附加不平整度。

5 结 论

笔者指出了在求解车桥耦合振动响应时，应将横梁效应作为自激扰因素考虑到车-桥振动系统中，提出了横梁效应引起的不平整度的简化计算模型，给出了考虑横梁效应的车-桥系统耦合振动求解方法，并通过算例进行了分析，得到了如下结论：

1)横梁效应实际上是由于桥面板刚度的变化所引起的附加桥面不平整度，这种附加不平整度是与车-桥系统振动耦合在一起的，求解时在每个时程点上需进行迭代计算。

2)横梁效应计算时可将桥面系等效成变刚度弹性层，其刚度变化规律与余弦函数类似，可采用式(9)近似模拟。

3)参数γ是影响横梁效应的重要因素，通过对5个不同的γ值的车-桥耦合振动动力响应进行计算，得出横梁效应随γ的增大而不断增大，呈高次变化趋势。

4)当γ<0.6时横梁效应并不明显，此时车-桥系统耦合振动可不计入横梁效应。

[1] 林梅，肖盛燮. 桥梁车辆振动分析理论评述[J].重庆交通学院学报，1998，17(3)：1-9.

LIN Mei, XIAO Shengxie. A discussion on vibration analysis theories of highway bridges and vehicles[J].JournalofChongqingJiaotongUniversity, 1998, 17(3)：1-9.

[2] 《中国公路学报》编辑部. 中国桥梁工程学术研究综述2014[J]. 中国公路学报，2014,27(5)：1-96.

Editorial Department of China Journal of Highway and Transport. Review on china’s bridge engineering research：2014[J].ChinaJournalofHighwayandTransport, 2014, 27(5)：1-96.

[3] 李小珍，强士中. 列车-桥梁耦合振动研究的现状与发展趋势[J]. 铁道学报，2002，24(5)：113-120.

LI Xiaozhen, QIANG Shizhong. State of the art review and trend of studies on vehicle-bridge interaction[J].JournaloftheChinaRailwaySociety, 2002, 24(5)：113-120.

[4] 易晋生，顾安邦，王小松.车桥耦合振动理论在桥面不平整度研究中的应用[J].重庆交通大学学报(自然科学版)，2013，32(4)：560-563.

YI Jinsheng, GU Anbang, WANG Xiaosong. Application of vehicle-bridge coupling vibrations theory in the study of bridge surface roughness[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2013, 32(4)：560-563.

[5] 黄立葵，盛灿花. 车辆动荷系数与路面平整度的关系[J].公路交通科技， 2006，23(3)：27-30.

HUANG Likui, SHENG Canhua. Relationship between vehicle dynamic amplification factor and pavement roughness[J].JournalofHighwayandTransportationResearchandDevelopment, 2006, 23(3)：27-30.

[6] FRYBA L.铁路桥梁动力学[M]. 齐法琳，孙宁，等译.北京：科学出版社，2007.

FRYBA L.DynamicsofRailwayBridges[M]. QI Falin, SUN Ning, et al. Translation. Beijing：Science Press, 2007.

[7] 王帆. 钢管混凝土拱桥车-桥耦合振动分析[D]. 哈尔滨：哈尔滨工业大学，2011.

WANG Fan.Vehicle-BridgeCoupledVibrationAnalysisofConcrete-FilledTubeArchBridge[D]. Harbin：Harbin Institute of Technology, 2011.

[8] 樊小虎，吴红林. 车桥耦合振动研究方法综述[J]. 科学技术与工程，2009，9(14)：4090-4099.

FAN Xiaohu, WU Honglin. Literature review of addressing interaction of vehicle-bridge vibration[J].ScienceTechnologyandEngineering, 2009, 9(14)：4090-4099.

[9] Yang Y B, Wu Y S. A versatile element for analyzing vehicle-bridge interaction response[J].EngineeringStructures, 2001, 23(5)：452-469.

(责任编辑：谭绪凯)

Influence of Crossbeam Effect on Vehicle-Bridge Coupled Vibration

WANG Fan1, WU Honglin2

(1. T. Y. Lin International Engineering Consulting (China) Co. Ltd., Chongqing 401121, P. R. China; 2. School of Communication Science & Engineering, Harbin Institute of Technology, Harbin 150090, Heilongjiang, P. R. China)

The simplified calculation model of additional roughness caused by crossbeam effect was proposed; the solution method for the vehicle-bridge coupled vibration considering the crossbeam effect was given. The problem that the modal synthesis method using truncated mode can’t reflect the vibration of bridge structures such as crossbeam and deck was solved. And different results considering the crossbeam effect or not were comprised and analyzed by case study. The non-dimensional parameterγdescribing the change aptitude of deck system’s elastically supporting stiffness was introduced at the same time, and its influence on the vehicle-bridge coupled vibration was also studied. The results show that crossbeam effect is coupled with the vehicle-bridge vibration system, and its effect value increases with the increase of parameter γ according to high order.

bridge engineering; vehicle-bridge coupled vibration; crossbeam effect; additional roughness; modal synthesis method; elastically supporting stiffness

10.3969/j.issn.1674-0696.2017.04.02

2016-02-17；

2016-10-15

王 帆(1987—)，男，四川广安人，工程师，主要从事桥梁设计及桥梁动力特性方面的研究。E-mail：wangfan@tylin.com.cn。

U441+.3;O319.56

A

1674-0696(2017)04-007-05