基于A*算法的四轴飞行器三维路径规划仿真
2017-04-20王佳琪宗成星
陆 亮, 王佳琪, 宗成星, 赵 萍
(合肥工业大学 机械工程学院,安徽 合肥 230009)
基于A*算法的四轴飞行器三维路径规划仿真
陆 亮, 王佳琪, 宗成星, 赵 萍
(合肥工业大学 机械工程学院,安徽 合肥 230009)
在机器人智能控制的研究中,路径规划是移动机器人研究的重要内容,而四轴飞行器是移动机器人的典型代表。文章以A*算法为基础,通过四轴飞行器的动力学和运动学建模,提出了一种新的四轴飞行器三维路径规划方法。首先通过A*算法在三维空间内寻径;然后提取该路径的每个关键节点;即四轴飞行器飞行方向改变的节点;最后结合四轴飞行器建模得出完成该段路径的电机控制策略的路径规划。仿真实验结果表明,四轴飞行器可以通过A*算法及其数学模型完成所需的路径规划要求。
四轴飞行器;航迹规划;避障;A*算法
四轴飞行器是一种由4个对称旋翼式的飞行引擎驱动,通过改变电机转速获得旋转机身的力从而调整自身姿态的智能机器人,具有结构简单、操纵方便以及机动灵活等优点。在此基础上发展的飞行器航拍、避障、搜救等应用也是当今国际上研究的热点[1-6]。国内外很多学者和研究机构通过对四轴飞行器进行动力学和运动学分析,建立系统的数学模型[2],并提出各种控制算法和设计飞行控制系统进行验证。
文献[3]提出了一种基于融合光流算法的四轴飞行器单目视觉避障算法,并进行了实验验证,证明了该算法实时避障性好、避障精确度高;文献[4]提出了一种基于蚁群算法的移动机器人路径规划技术,通过引力函数构建一种新的启发因子,减少了劣质解的产生并加快了算法的收敛速度,但在一定程度上降低了算法的全局搜索能力;文献[5]提出了基于可视图法的无人机避障路径规划方法,并得出了避障路径,但由可视图法得出的最短避障路径必须经过长方体障碍物的顶点,因此并不是最优路径。本文提出利用A*算法进行路径规划,关联飞行控制系统来控制电机,进而完成整个路径的循迹避障功能。
1 数学建模
1.1 结构与控制原理
对四轴飞行器的姿态控制进行运动学和动力学特性分析,三维建模四轴飞行器在低速或者静态环境下的简化动力学模型。其4个旋翼分别以对称十字架结构布置,分为前后和左右2组。2组旋翼的旋转方向相反,可相互抵消反扭力矩。
当4个电机的转速相等且旋翼所产生的升力之和等于飞行器自身重力时,飞行器处于悬停状态;在此基础上,当其中1个电机转速增大或减小,对角线上电机转速等量地减小或增大时,飞行器将向电机转速减小的一侧倾斜,产生俯仰运动或者滚转运动。飞行器的任意一组对角线上的电机转速等量增大或减小而另一组对角线上的电机转速不变时,飞行器将产生偏航运动。
1.2 姿态建模
以四轴飞行器的俯仰、横滚以及偏航3种状态矩阵连乘得到姿态变换矩阵。
假设先转动偏航角度ψ,再转动俯仰角度θ,最后转动横滚角度φ。由此得到的姿态变换矩阵R为:
(1)
其中,φ、θ、ψ分别为横滚角、俯仰角、偏航角。
飞行器的姿态解算是增量式方法,即
(2)
其中,εn和εn-1分别为第n次和n-1次的姿态变换矩阵;Rn为第n次的姿态解算矩阵。
又因为四轴飞行器对角度有很高的采样频率,所以每次的角度变化很小,因此可以将姿态变换矩阵R进行简化[6],即
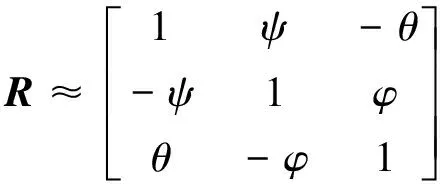
(3)
由此得到不同姿态变换顺序的变换矩阵的近似结果相近,均为(3)式。
为简化算法,模型偏航角选为0,因此增量变换矩阵为:
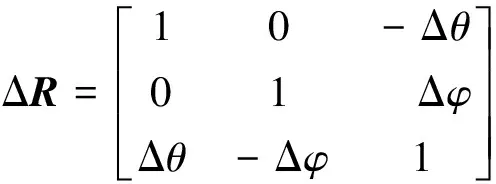
(4)
增量式的姿态解算运算如下:
(5)
1.3 动力学建模
本文模型借鉴文献[6]的研究,建立了飞行器4个电机所产生的升力与飞行器运动参数之间的关系,得到四轴飞行器的运动学方程如下:
(6)
(7)
其中,x、y、z分别为X、Y、Z方向上的位移;u1、u2、u3、u4为四轴飞行器4个电机的控制量;F1、F2、F3、F4分别为飞行器1、2、3、4旋翼所产生的升力;Iφ、Iθ、Iψ分别为飞行器绕机体坐标系X、Y、Z3个坐标轴的转动惯量;m为四轴飞行器的质量;c=KF/KM,KF为旋翼转速和四轴飞行器升力的比例系数,KM为旋翼转速和四轴飞行器反扭矩的比例系数。
根据文献[2]的研究得出了四轴飞行器的升力与旋翼转速的平方成正比关系,即
(8)
因此可以通过飞行器动力学模型先求出F1、F2、F3、F4,然后通过(8)式得到电机转速。
2 算法描述
2.1 四轴飞行器路径规划算法
在三维空间中求解移动机器人最优路径的方法有很多,如A*算法[7]、D*算法[8]、进化算法[9]等,在众多求解最优路径的方法中,A*算法简单、有效,并且得到了广泛的应用[10],因此本文采用A*算法进行四轴飞行器的路径规划。
A*算法是一种启发式的搜索算法,即当机器人进行移动时,对机器人当前位置下所有可以选择的到达下一位置的路径进行评估,得到当前最好的路径,然后在下一位置进行搜索,直至找到目标。该算法方便快捷且具有较高的针对性,只需搜索部分空间即可达到缩小搜索范围、降低问题复杂度的目的,拥有很高的路径搜索效率[11]。
A*算法的表达式为:

(9)
其中,f(n)为从初始节点经由节点n到目标节点的估价函数;g(n)为在状态空间中从初始节点到n节点的实际代价;h(n)为从n节点到目标节点最佳路径的估计代价。根据估价函数每次判断的代价大小,决定先采用哪种路径[12]。
A*算法流程图如图1所示。
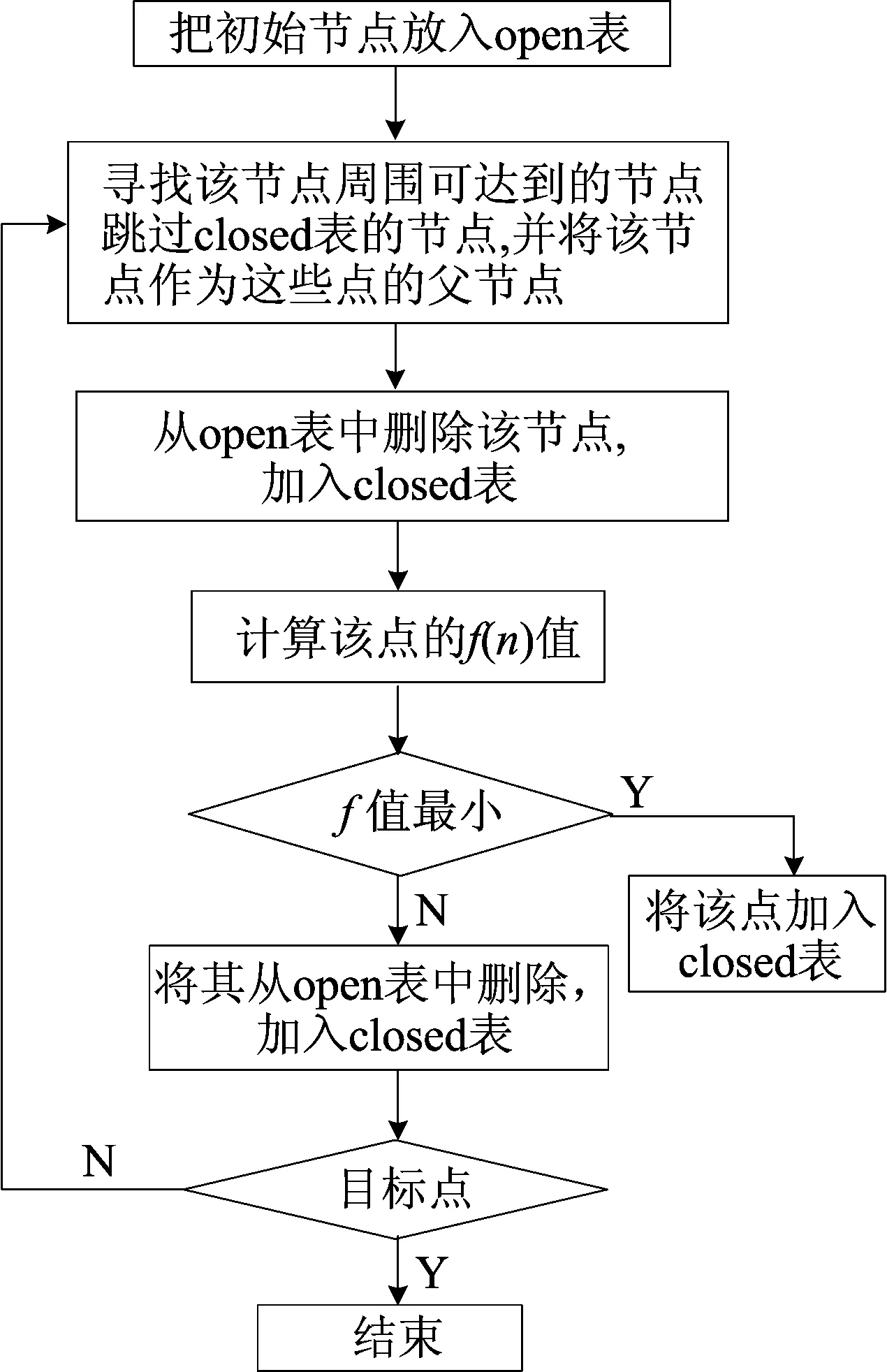
图1 A*算法流程
2.2 场景建模
由上述理论可知,为了通过A*算法在空间障碍模型中给四轴飞行器规划出一条最优路径,必须提供障碍点和非障碍点的信息。本文采用了三维0-1矩阵(1表示障碍点,0表示非障碍点)的方式储存障碍点与非障碍点的信息,并且使障碍信息矩阵和空间障碍模型的障碍分布情况一一对应,即一个n×n×n的障碍空间可以看成是n+1行、n+1列、n+1层的三维全0矩阵,在其中加入障碍的过程,可以视为在该三维矩阵中与此障碍在障碍空间中的X、Y、Z的坐标相对应的y+1行、x+1列、z+1层的0改为1的过程。因此,在障碍空间构建完成后,也就得到了与之对应的障碍信息矩阵。
在算法提取障碍矩阵的信息时,1作为障碍点代价视为无穷大。
空间障碍模型如图2所示。

图2 空间障碍模型
以图2中未填黑区域为例,简单说明本文的场景建模策略,该区域的障碍信息矩阵Z为:
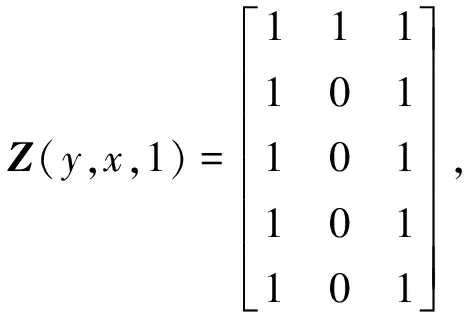

由以上3×5×3的障碍信息矩阵和图2所示的10×10×10的空间障碍模型中未填黑的2×4×2的区域可以明显地看出,矩阵的行、列、层与三维空间的X、Y、Z坐标是一一对应关系。
2.3 碰撞检测
在空间障碍模型中,内部的障碍物一般不是规则的几何图形[13]。因此本文提出了一种通过长方体包络不规则图形来简化模型并通过线与面的位置关系来解决飞行器飞行路径与障碍物之间碰撞检测问题的方法。
球形障碍简化模型如图3所示,图3表示了障碍的包络简化方法,即根据障碍物的轮廓,画出障碍物的外接长方体。该建模方法虽然在一定程度上扩大了障碍域,但是大大提升了算法的效率和飞行器飞行的安全性[14]。
在简化模型的基础上,四轴飞行器与障碍物的碰撞则转化为四轴飞行器的路径与障碍物(长方体)的位置关系问题,即直线和面的空间位置关系,四轴飞行器的路径与立方体的面相交则发生碰撞,反之则不发生碰撞。因此仅需计算路径点之间的连线与障碍物长方体之间的位置关系,即可判断四轴飞行器是否与障碍物发生碰撞[15]。

图3 球型障碍简化模型
2.4 基于A*算法四轴飞行器控制建模
为了达到能在设定的场景中控制四轴飞行器完成给定轨迹飞行的目的,结合A*算法原理与四轴飞行器的数学模型,本文提出了一种将飞行器4个电机转速与运动规律相对应的数学模型。该模型给定起始与终止目标点坐标,给定电机响应时间,推导出以此为间隔的转速响应函数。同时,若给出一段连续的4电机转速响应函数,飞行器能输出位置和时间相对数据。因此,可以提前扫描空间信息,提取有效参数,通过A*算法找出合适路径,返回电机转速响应函数,通过飞行控制器使飞行器执行由算法运算得到给定的轨迹。
A*算法每次只有上、下、左、右、前、后6个搜索方向,即只有沿X、Y、Z坐标轴方向的位置变化,因此所得到的路径必为直线段。完成四轴飞行器沿直线段路径的飞行有如下2种策略。
(1) 四轴飞行器按照给定路径从起点到终点飞行,中途没有任何停顿,一次性飞完全程。
(2) 先提取给定路径中的各个直线段部分,四轴飞行器从起点开始,每飞完一段直线段后进行短暂的悬停,再进行下一直线段的飞行,直至到达目标点。
考虑到飞行器飞行的稳定性问题,若按照策略(1)飞行,需要将路径进行优化,但这无疑会增加飞行器控制的难度和算法的复杂度。
因为相比于一般的飞行器,四轴飞行器具有悬停这种优良的飞行特性,能够良好地适应飞行策略(2),所以本文选用策略(2)完成给定直线段路径的飞行。
为了满足策略(2)的飞行要求,本文对四轴飞行器的位移、速度、加速度函数作出了相应的规定:① 四轴飞行器的初始位移为0;② 四轴飞行器的最终位移为X、Y或Z轴方向上所要求的位移;③ 四轴飞行器的初始速度为0;④ 四轴飞行器的末端速度也为0;⑤ 四轴飞行器的初始加速度为0;⑥ 四轴飞行器的末端加速度为0。
为了满足这6个条件,选五次多项式作为四轴飞行器在X、Y、Z轴方向上的运动学方程,即
f(t)=a0t5+a1t4+a2t3+a3t2+a4t+a5
(10)
其中,f(t)为飞行器的位移;t为飞行器完成该段位移所需的时间。
为了求出位移方程,需求解的方程组如下:

(11)
其中,l为从当前位置到目标位置的长度。解该方程组得到待定参数a0、a1、a2、a3、a4、a5,即可得到X、Y、Z轴方向上的位移方程。
根据牛顿第二定律可得:
(12)
根据飞行器动力学方程可得u2、u3,因为不考虑偏航角,所以u4=0;由以上内容可以求解得F1、F2、F3、F4。
综上可得:
(13)
结合给定位移长度与完成该段位移所需要的时间,即可得到四轴飞行器的4个电机的动态实时转速,从而控制飞行器的运动。
对质量为0.15 kg、旋翼到四轴飞行器中心的距离为0.15 m、Iφ和Iθ皆为0.033 kg·m2、KF为3×10-7N·s2、KM为1.12×10-7N·s2、g为9.8 m/s2时的四轴飞行器进行仿真。飞行器在X、Y、Z轴方向上2 s内飞行1 m时,4个电机的转速变化曲线分别如图4~图6所示。

图4 X轴方向上4个电机的转速变化曲线
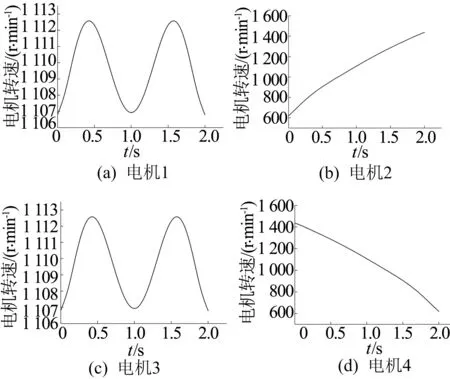
图5 Y轴方向上4个电机的转速变化曲线

图6 Z轴方向上4个电机的转速变化曲线
2.5 四轴飞行器A*算法路径规划
由A*算法的原理可知,作为启发式全局搜索算法,A*算法是通过估价函数f(n)从每个位置所有遍历的点中选取最优的点,然后形成最优路径。
本文所选用估价函数的估计代价为:

其中,xg、yg、zg为目标位置的坐标;xn、yn、zn为当前位置的坐标。
本文设四轴飞行器飞行的初始节点为S,目标节点为G,飞行器从初始节点开始飞行,有上、下、左、右、前、后6种飞行策略。设初始节点坐标为(x,y,z),则6种飞行策略所能到达位置的坐标分别为(x,y,z+1)、(x,y,z-1)、(x,y-1,z)、(x,y+1,z)、(x+1,y,z)、(x-1,y,z)。通过估价函数f(n)就可以在这6个点中选出最优的飞行策略,然后执行此飞行策略到达指定位置,重复上述寻径方法,直至找到一条到达目标位置的路径。
通过A*算法得到一条切实可行的路径之后,可以提取该路径的各个关键点,即直线段的每个端点为p1,p2,…,pk-1,pk,…,pn-1,pn。设pk=(xk,yk,zk),pk-1=(xk-1,yk-1,zk-1),pk与pk-1在X、Y、Z方向上的距离分别为xk-xk-1、yk-yk-1、zk-zk-1,然后结合四轴飞行器的建模即可获得四轴飞行器电机控制策略。
3 仿真实验及实验结果分析
A*算法躲避不规则障碍路径规划的仿真模型如图7所示,其中左侧点代表初始节点,右侧点代表目标节点。由仿真结果可知,A*算法可以得到一条能够到达目标位置且与所设计的障碍不相碰撞的路径。

图7 A*算法避障路径规划
下面以图7所示情况为例,结合四轴飞行器的建模,提出对飞行器的电机转速要求。
图7路径的关键节点为:p1=(0,0,0),p2=(4,0,0),p3=(4,2,0),p4=(4,2,2),p5=(8,2,2),p6=(8,7,2),p7=(8,7,3),p8=(8,9,3)。
因为建模时本文提出的飞行要求而选定的位移函数的限制,所以四轴飞行器在X、Y、Z轴方向上飞行单位长度(1 m)所需的时间必须大于1 s。为了方便计算,本文假设四轴飞行器在X、Y、Z轴方向上飞行1 m所需的时间为2 s,由以上的关键点可以得出飞行策略如下:
(1)X轴方向上飞行4 m,飞行时间为8 s;
(2)Y轴方向上飞行2 m,飞行时间为4 s;
(3)Z轴方向上飞行2 m,飞行时间为4 s;
(4)X轴方向上飞行4 m,飞行时间为8 s;
(5)Y轴方向上飞行5 m,飞行时间为10 s;
(6)Z轴方向上飞行1 m,飞行时间为2 s;
(7)Y轴方向上飞行2 m,飞行时间为4 s。
每当四轴飞行器进行飞行方向的调整时有一定的悬停姿态调整时间,为了减少对四轴飞行器飞行流畅性的影响,将悬停进行姿态调整的时间设为四轴飞行器控制器的采样周期,一般为0.1 s,因此完成图7路径的飞行,共计进行6次悬停姿态调整,共计花费0.6 s,本次飞行花费时间为40.6 s。
由上述飞行策略可以得到四轴飞行器的电机控制策略如图8所示。旋翼到四轴飞行器中心的距离为0.15 m,Iφ和Iθ为0.033 kg·m2,KF为3×10-7N·s2,KM为1.12×10-7N·s2,g为9.8 m/s2。四轴飞行器进行姿态调整的时间节点分别为8.0~8.1 s、12.1~12.2 s、16.2~16.3 s、24.3~24.4 s、34.4~34.5 s、36.5~36.6 s ,共6处。
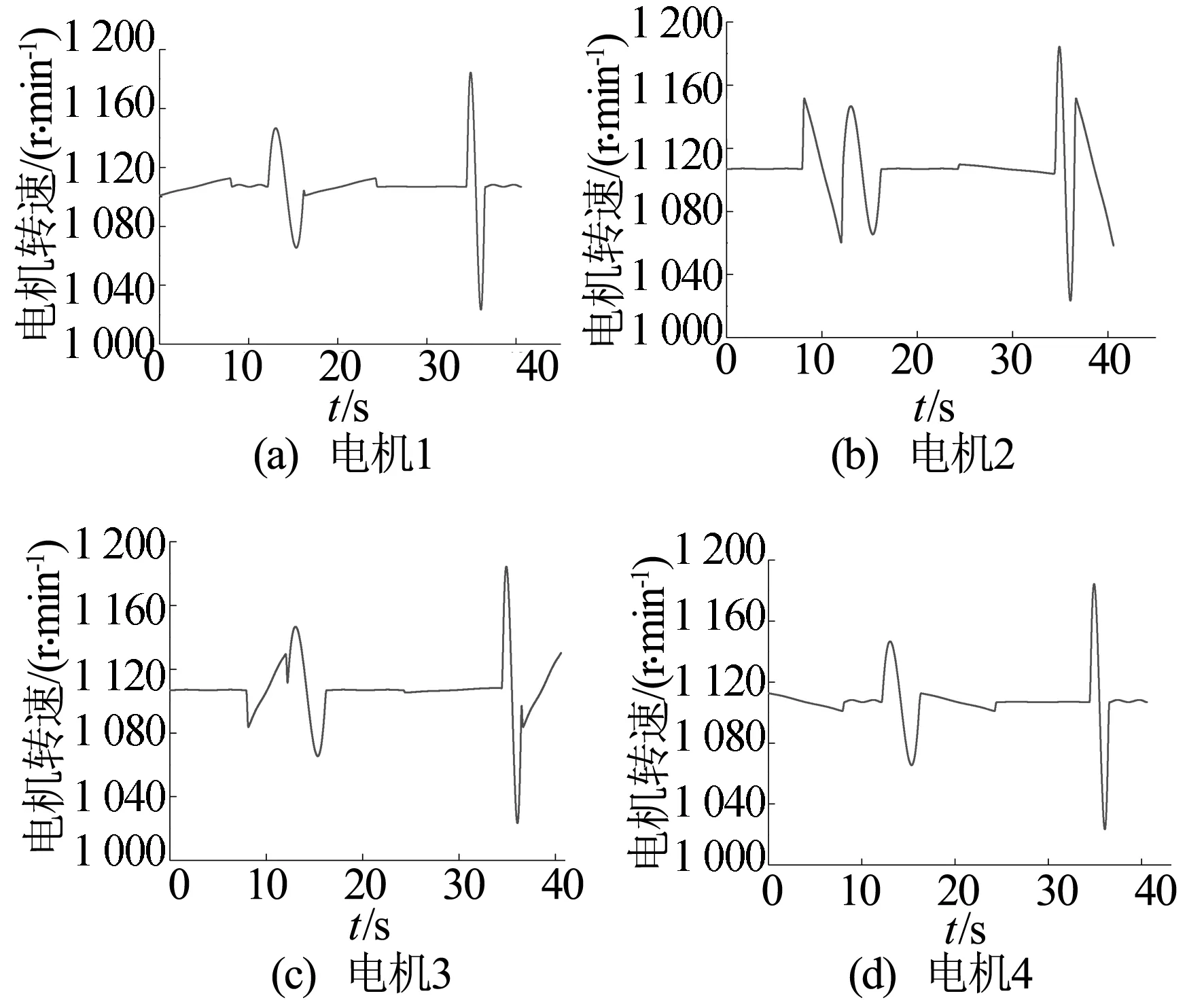
图8 飞行器完成图7路径时4个电机的转速变化曲线
4 结 论
本文通过四轴飞行的姿态和动力学建模,构建了四轴飞行器的姿态变换和4个旋翼转速与其位置变换之间的关系。通过三维矩阵构建三维空间模型,并通过A*算法得出该三维空间模型中的最优路径,从而得到四轴飞行器所有经过的路径节点,再将相邻节点求差得出它们之间的位移,最后将各相邻节点的位移与四轴飞行器的模型相对应,便可以在理想状况下通过控制飞行器的旋翼转速使四轴飞行器在三维空间中完成避障路径规划。
仿真实验表明,四轴飞行器可以通过A*算法实现三维空间的路径规划。下一步主要有2个方面的工作:① 搭建四轴飞行器的试验平台,将本文所提出的算法在四轴飞行器的试验平台上加以试验验证;② 将算法改进,使算法能适应不同条件下的避障需求。
[1] LIU W,ZHENG Z,CAI K Y.Adaptive path planning for unmanned aerial vehicles based on bi-level programming and variable planning timeinterval[J].Chinese Journal of Aeronautics,2013,26(3):646-660.
[2] 聂博文.微小四旋翼无人直升机建模及控制方法研究[D].长沙:国防科技大学,2006.
[3] 赵海,陈星池,王家亮,等.基于四轴飞行器的单目视觉避障算法[J].光学精密工程,2014,22(8):2232-2240.
[4] 孙纯哲,桂贵生,韩东,等.基于蚁群算法的移动机器人路径规划研究与应用[J].合肥工业大学学报(自然科学版),2006,29(10):1208-1211.
[5] KUWATA Y,HOW J.Three dimensional receding horizon control for UAVs[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Reston,VA:AIAA,2004:2100-2113.
[6] 程学功.四轴飞行器的设计与研究[D].杭州:杭州电子科技大学,2012.
[7] HART P E,NILSSON N J,RAPHAEL B.A formal basis for the heuristic determination of minimum costs paths[J]. IEEE Transactions on Systems Science and Cybernetics,1968,4(2):100-107.
[8] KRUUSMAA M.Global navigation in dynamic environments using case-based reasoning[J].Autonomous Robots,2003,14(1):71-91.
[9] 吴梅,刘小刚.基于进化算法的无人飞行器路径规划研究[J].弹箭与制导学报,2006,26(3):231-234.
[10] 钱红昇,葛文锋,钟鸣,等.基于分层的改进A*算法在路径规划中的应用[J].计算机工程与应用,2013,50(7):225-229.
[11] DVORKIN E N,MEDINA F M.Finite element models for analyzing the straightening of steel seamless tubes[J]. Journal of Engineering for Industry,1989,111(4):351-355.
[12] 秦玉鑫,王红旗,杜翠杰,等.基于双层A*算法的移动机器人路径规划[J].制造业自动化,2014,36(12):21-25.
[13] GALINDOA G,MADRIGAL J A F,GONZLE J.Robot task planning using semantic maps[J].Robotics and Autonomous Systems,2008,56(11):955-966.
[14] 文中华,黄巍,刘任任,等.模型检测规划中的状态之间的可达关系研究[J].计算机学报,2012,35(8):1634-1643.
[15] 黎萍,朱军燕,彭芳,等.基于可视图与A*算法的路径规划[J].计算机工程,2014,40(3):193-195,200.
(责任编辑 胡亚敏)
Simulation of 3D path planning approach for quad-rotor helicopter based on A*algorithm
LU Liang, WANG Jiaqi, ZONG Chengxing, ZHAO Ping
(School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China)
Path planning is an important part of the research on mobile robot in the research of robot intelligent control, and the quad-rotor helicopter is a typical representative of the mobile robot. In this paper, by dynamics modeling of quad-rotor helicopter, a new kind of path planning method of the quad-rotor helicopter is presented based on A*algorithm in 3D space, and then each key node of the path is extracted, which controls the quad-rotor helicopter flying direction. Finally, the path planning is achieved with the motor control strategy which is calculated by key nodes and dynamic modeling of quad-rotor helicopter. The results of simulation experiments show that with A*algorithm and its mathematical model, the requirements of obstacle avoidance and path planning can be satisfied.
quad-rotor helicopter; path planning; obstacle avoidance; A*algorithm
2015-08-14;
2015-10-09
国家自然科学基金资助项目(51405128);安徽省自然科学基金资助项目(1508085QE82)
陆 亮(1992-),男,浙江东阳人,合肥工业大学硕士生; 赵 萍(1988-),女,山东烟台人,博士, 合肥工业大学副教授,硕士生导师.
10.3969/j.issn.1003-5060.2017.03.004
TP391.9
A
1003-5060(2017)03-0304-06
