六自由度串联机器人动态误差分析
2017-04-20侯小雨朱华炳王鲁平
侯小雨, 朱华炳, 王鲁平
(合肥工业大学 机械工程学院,安徽 合肥 230009)
六自由度串联机器人动态误差分析
侯小雨, 朱华炳, 王鲁平
(合肥工业大学 机械工程学院,安徽 合肥 230009)
由于机器人在工作过程中受负载、连杆自重等因素影响,其连杆产生变形会引起末端执行器的位置误差。针对该问题,文章以FANUC M-10iAe机器人为研究对象,采用仿真与实验相结合的方法,以提高机器人定位精度为目标展开研究。在ADAMS环境中进行动力学仿真,对机器人工作过程中变载荷引起的动态误差进行分析;通过自主设计的测量装置及变载荷方盒进行试验,结果证实了动力学仿真的准确性;在误差分析结果的支撑下,设计开发了基于人机交互的误差补偿界面并通过了实例验证。
串联机器人;柔性;动态误差;ADAMS仿真;负载;误差补偿界面
随着工业技术的不断发展,串联机器人作为一种典型的柔性自动化设备已被广泛应用于焊接、码垛、喷涂等领域,引领产业升级和转型。目前工业机器人的重复定位精度较高,而绝对定位精度一般都比较低[1],这样的绝对定位精度水平已不能满足一些高精度操作作业场合的需要。国内外从20世纪80年代就开始了这方面的研究工作,形成了多种误差分析方法,通过标定的方法提高机器人绝对定位精度[2-4],研究机械臂自重和负载变化引起机器人末端执行器的位置误差[5-7]。
本文针对工业机器人在不同码垛任务中负载的不同,考虑机器人的连杆一般都具有一定的柔性,通过分析末端负载这一动态因素对机器人精度造成的影响,达到对误差进行预测的目的;设计开发的误差补偿界面可以为机器人误差补偿提供参考,进而提高机器人的绝对定位精度。
1 动态误差分析
1.1 FANUC M-10iAe机器人误差传递模型
根据D-H参数法,确定了FANUC M-10iAe机器人各关节坐标系,将连杆坐标系按坐标系编号依次变换,建立四阶变换矩阵表征其与前一杆件坐标系的变换关系,得到机器人连杆参数的D-H参数表,见表1所列。

表1 FANUC M-10iAe机器人D-H参数表
由D-H参数和齐次变换公式可依次求得两杆之间的位姿矩阵Ti,进而得出机器人从基座到末端执行器的总齐次变换公式为:
(1)
其中,nx、ny、nz为末端执行器法向矢量;ox、oy、oz为方向矢量;ax、ay、az为接近矢量;px、py、pz为位置坐标。
由(1)式可得出末端执行器位置坐标与各关节转角的关系为:
200cosθ1cosθ2+600cosθ1,
200sinθ1cosθ2+600sinθ1,
1.2 FANUC M-10iAe机器人动力学模型
FANUC M-10iAe机器人是一种六自由度串联机器人,具有6个转动关节。其本体由基座、立柱、大臂、小臂、手腕、手部组成,各转动关节与减速器相连并由伺服电机驱动,可以满足驱动力矩较大和运动定位准确的要求。利用SolidWorks软件对该机器人进行三维实体建模,得到机器人虚拟装配体,然后导入ADAMS中。
机器人的2、4连杆因其杆长的原因产生的变形量比其他连杆大,对末端精度造成的影响也就更大,同时为了适当简化模型,本文仅对三维实体模型中的2、4连杆进行柔性化处理。首先利用ADAMS/Flex柔性体模块生成2、4连杆的柔性体[8],提取六阶模态,生成模态中性文件MNF,然后将MNF文件导入到ADAMS软件中替代原来的刚性构件,得到刚柔耦合动力学模型,如图1所示。

图1 FANUC M-10iAe机器人刚柔耦合动力学模型
1.3 驱动函数
在本文研究的机器人码垛任务中,为了依据预先规划的轨迹对动力学模型进行驱动,可近似认为机器人在固定时间内的运动是逐步和阶跃的。
在Matlab中模拟实际码垛完成轨迹规划,然后利用规划轨迹中各关节转角的变化值生成样条曲线,即各关节的驱动函数[9]。具体步骤如下:利用Matlab在码垛任务过程中每隔0.056 s计算1次各关节转角,得到各关节转角变化数值,在ADAMS中通过Test Data 外部输入数据依次导入各关节角位移数值,并创建相应的Spline样条函数曲线。其中关节1的样条函数曲线SplneE-1如图2所示。其余5个关节的样条函数曲线创建方法同上,此处不再赘述。最后将6个关节样条函数依次施加到对应关节转动副上,完成对动力学模型的驱动[10]。

图2 关节1样条函数曲线Spline-1
1.4 基于实际工况的机器人末端载荷的施加
研究对象FANUC M-10iAe机器人可搬运质量的最大值为10 kg,结合实际验证试验方案中末端载荷的变化情况,设定末端载荷变量的10个取值。在ADAMS中分别针对10组末端载荷变量进行模拟仿真,得到仿真曲线,下面仅列出末端载荷为8.889 kg时末端执行器对称中心处位移曲线,如图3所示。

图3 末端载荷为8.889 kg时末端位移仿真曲线
通过对比末端执行器对称中心处Marker点的坐标和末端执行器的理论目标点位置坐标(750.000,-500.000,250.000),可以得到不同末端载荷下动态误差量的大小,见表2所列。
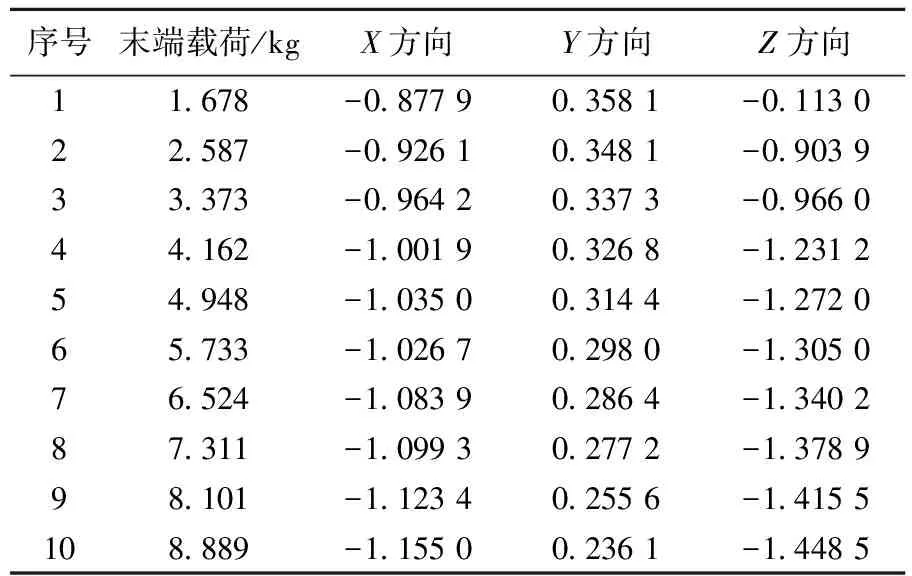
表2 动力学仿真得到的动态误差值 mm
2 误差验证试验
2.1 试验方案设计与数据采集
本试验通过自主设计的测量装置及变载荷方盒,借助FANUC M-10iAe机器人进行试验研究。其中测量装置由3个SGC-W10微位移光栅传感器和1个测量台架组成。3个传感器分别测量X、Y和Z方向的位移偏差;方盒内部可按需要装入0~9枚砝码,以此来调节末端载荷的质量[11]。通过该试验可以得到机器人动态误差与末端载荷的关系。
在试验过程中需要通过示教的方法运行并控制末端执行器姿态不发生改变,以保证3个传感器测量头始终与方盒3个表面分别垂直,避免末端执行器中心点产生旋转量而对试验结果产生影响。本试验采用的传感器分辨率为1 μm,FANUC M-10iAe机器人重复定位精度为±0.08 mm,因此选择该位移传感器测量机器人定位精度是满足要求的。传感器输出的TTL方波通过数显表和RS235串口与计算机通讯,传感器输出信号用Data Acquisition数据采集工具箱进行采集和处理。试验过程中,机器人末端执行器重复运行至试验数据测量点,传感器测得X、Y和Z方向的位置偏移量由计算机记录并保存。具体试验流程如图4所示。

图4 试验流程
2.2 试验数据处理与分析
试验过程中机器人自定义空间坐标原点位于基座的内部,其具体位置无法测量,故此处采用距离误差原理对试验数据进行处理。对测量组的试验数据分别求解其在空间坐标系中算术平均误差值,将这些相对测量台架的误差偏移项作为对仿真数据验证的评价指标[12]。由于试验结果与动力学仿真得到的结果需要进行对比,故此处对X、Y和Z方向上的算术平均误差值分别进行求解,公式如下:
(2)
其中,xi、yi、zi为试验测得3个传感器的位置偏移量;x、y、z为方盒3个测量面理论上引起3个传感器的位置偏移量;k为试验测量次数。
下面展开对x、y、z的计算工作,本文仅对X、Z方向的计算提供图解,如图5所示。

图5 X、Z方向计算图解
首先利用机器人示教盒上读出试验点机器人的位置数据(xd,yd,zd),测量变载荷方盒的外形尺寸值xf、yf、zf和方盒安装板上的机器人末端执行器安装孔深度h,求出在试验点处方盒的3个测量面与机器人坐标原点的理论距离(xa,ya,za),计算公式如下:
(3)
测出3个传感器测量头在世界坐标系下的坐标(xc,yc,zc),即可求得方盒3个测量面理论上引起3个传感器的位置偏移量,分别为:
(4)
由(4)式计算得出x=1.26 mm,y=0.51 mm,z=6.04 mm。
将上述数据和试验测得的数据代入(1)式,即可得出每个测量组在X、Y、Z方向上的算术平均误差值,见表3所列。

表3 X、Y、Z方向上的平均误差值 mm
在X、Y、Z方向上对仿真与试验数据的误差均值进行对比,由于篇幅有限,本文仅列出X方向对比结果,如图6所示。
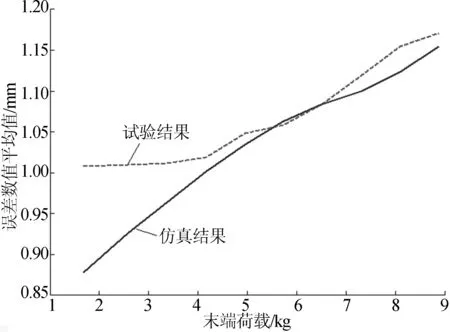
图6 X轴方向仿真结果与试验结果对比
由分析对比结果可知,动力学仿真对误差变化的预测趋势是正确的,即总体误差随着末端载荷的增大而增大。在X、Y、Z方向上试验误差均值相对于试验数据均值的偏差分别为3.44%、7.34%、15.16%。其中,Z方向上首组试验点仿真结果与试验结果相差较大,属于异常点,为了得到比较符合实际的拟合结果,需要除去Z方向上的首组数据,则Z方向上误差偏差降低至6.85%,该结果是比较符合实际情况的。
3 误差补偿界面
3.1 误差补偿界面的设计
针对机器人实际应用场合柔性较强的现状,本文设计的误差补偿界面具备的用户定义输入变量主要有4项,分别为目标机器人型号、末端载荷质量、误差量拟合方式、码垛作业区间。基于仿真与试验得到的综合误差情况,在用户自定义输入变量后完成补偿量的计算输出。误差补偿界面的布局如图7所示。

图7 误差补偿界面布局
实现补偿界面的基本机制是对控件的属性编程,通过回调函数(callback)来完成事件驱动。用户输入参数后通过句柄传递至运算模块,点击相应按钮控件,触发相应的计算和绘图功能,结果将在文本框与图形窗口进行显示。
为了通过有限次的变载荷模拟试验来预测机器人在负载允许范围内的误差变化情况,在Matlab中使用最小二乘法拟合各末端载荷与相应误差值的关系,然后利用拟合函数对不同负载影响下的误差量进行插值计算,得到对应负载的误差补偿量[7]。
3.2 误差补偿界面验证实例
为了直观地验证误差补偿界面功能的有效性,本次实验以1个质量为9.677 kg的工件为负载,具体步骤如下:
(1) 利用本文设计的试验方案,在变载荷方盒内加入1块质量为0.788 kg的砝码,使负载总质量达到9.677 kg,试验后对所得数据进行处理并记录。
(2) 启动误差补偿界面,在参数输入界面选择机器人型号FANUC M-10iAe、输入末端载荷质量9.677 kg、选择工作区间1及曲线拟合方式为三次多项式插值法,输入完成后开始计算,记录补偿量数值。
综上所述,得到试验数据处理结果与误差补偿量的计算结果,见表4所列。

表4 试验误差量与误差补偿量对比
由表4可知,在X、Y、Z方向上试验误差量与误差补偿量之间的偏差分别为0.002 6、0.031 3、0.164 6mm,两者的差异很小,可见该误差补偿界面计算的结果具有一定的可靠性。另外该误差补偿界面符合输入简单、显示直观的实际需求。用户可以选择在Matlab环境下保存所创建的图形用户界面,也可以通过mcc编译生成可独立运行的应用程序,这都将会拓展该误差补偿界面的应用场合。
4 结 论
本文基于特定的码垛工作轨迹,将六自由度机器人动态误差的研究转化为对末端执行器定位精度的研究,重点分析了末端载荷的变化对机器人末端执行器绝对定位精度的影响。通过对比试验结果和动力学仿真结果,说明根据刚柔耦合的动力学模型仿真得出的误差结果是比较准确的,从而也验证了动力学仿真对误差变化的预测趋势的正确性;应用验证实例证明了本文设计的误差补偿界面可以对不同负载影响下的误差进行插值计算,且结果具有一定的可靠性,可以为后续误差补偿提供参考,同时也为柔性生产条件下提高机器人精度提供了一种解决方案。
[1] 李定坤,叶声华,任永杰,等.机器人定位精度标定技术的研究[J].计量学报,2007,28(3):224-227.
[2] 龚星如,沈建新,田威,等.工业机器人的绝对定位误差模型及其补偿算法[J].南京航空航天大学学报,2012,44(增刊1):60-64.
[3]PARKIW,LEEBJ,CHOSH,etal.Laser-basedkinematiccalibrationofrobotmanipulatorusingdifferentialkinematics[J].IEEE/ASMETransactionsonMechatronics,2012,17(6):1059-1067.
[4] 张利,潘承毅,刘征宇,等.差动驱动机器人的一种航迹推算定位方法[J].合肥工业大学学报(自然科学版), 2010, 33(11):1605-1608,1622.
[5]VERDONCKW.Experimentalrobotandpayloadidentificationwithapplicationtodynamictrajectorycompensation[D].Leuven:KatholiekeUniversityLeuven,2004.
[6] 王一,刘常杰,任永杰,等.工业坐标测量机器人定位误差补偿技术[J]. 机械工程学报,2011,47(15):31-36.
[7]ZHOUJ,NGUYENHN,KANGHJ.Simultaneousidentificationofjointcomplianceandkinematicparametersofindustrialrobots[J].ProceedingofIEEEInternationalJournalofPrecisionEngineeringandManufacturing,2014,15(11):2257-2264.
[8] 戴洪光.基于ADAMS平台的柔性体仿真理论的若干研究[D].合肥:合肥工业大学,2008.
[9] 王鲁平.串联机器人多误差因素影响下定位精度分析及其误差补偿[D].合肥:合肥工业大学,2015.
[10] 朱龙英,陆宝发,成磊,等.刚柔耦合机器人仿真及振动分析[J].中国工程机械学报,2015,13(2):120-123.
[11] 秦磊.工业机器人定位精度与腕部载荷关系研究[D].合肥:合肥工业大学,2014.
[12] 南小海.6R型工业机器人标定算法与实验研究[D].武汉:华中科技大学,2008.
(责任编辑 胡亚敏)
Dynamic error analysis of 6-DOF serial robot
HOU Xiaoyu, ZHU Huabing, WANG Luping
(School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China)
Robot is affected by the factors such as load, link weight in the working process, of which links deformation makes the end actuator position error. In this paper, taking FANUC M-10iAe robot as the research object, the improvement of robot positioning accuracy is studied by using the method of simulation and experiment. The dynamic simulation in ADAMS environment is conducted, and the robot dynamic error caused by the variable load is analyzed. The tests using the self-designed measuring device and variable load box are done, and the result shows the accuracy of dynamic simulation. On the basis of the acquired error data, the error compensation interface based on human-computer interaction is designed and developed, and its effectiveness is validated by an example.
serial robot; flexibility; dynamic error; ADAMS simulation; load; error compensation interface
2015-08-27;
2015-12-31
合肥工业大学产学研校企合作资助项目(W2015JSKF0377)
侯小雨(1992-),男,安徽六安人,合肥工业大学硕士生; 朱华炳(1963-),男,安徽怀宁人,博士,合肥工业大学教授,博士生导师.
10.3969/j.issn.1003-5060.2017.03.003
TP242.2
A
1003-5060(2017)03-0299-05
