关于EnergyPlus通风管道换热数学模型的分析

彭吉，王如竹，Vojislav Novakovic

（1-上海交通大学制冷与低温工程研究所，上海 200240；2-挪威科技大学，特隆赫姆 7491）

关于EnergyPlus通风管道换热数学模型的分析

彭吉*1，王如竹1，Vojislav Novakovic2

（1-上海交通大学制冷与低温工程研究所，上海 200240；2-挪威科技大学，特隆赫姆 7491）

本文针对能耗模拟软件EnergyPlus中通风系统中的管道换热数学模型，进行了不同工况下的换热计算，通过实验研究了对应工况下的空气温度和热损失功率的实际变化；对EnergyPlus管道换热数学模型进行定量分析，并针对EnergyPlus软件中需使用固定传热系数的特点进行定量运行分析。实验和计算结果表明，EnergyPlus管道换热数学模型在稳定工况下温度变化和热损失功率的计算结果与实际结果接近；而在工况条件变化的情况下则与实际结果相差较大。而EnergyPlus软件中需使用固定传热系数的特点，将导致温度变化和热损失功率的计算结果容易与实际运行的结果差别较大。

EnergyPlus；通风系统；管道换热；热损失；数学模型；固定传热系数

0 引言

建筑能耗的增长是经济发展的必然结果，但是由于我国目前能源利用率比较低，采暖和空调占用建筑总能耗的比重仍然很大，因此建筑节能潜力巨大，任务也相当艰巨[1-2]。在建筑能耗中，不必要的能量损失和温度变化不可忽视。

随着建筑的发展，建筑中通风管道的长度可能会很长，因此通风管道内部空气会与外界进行能量交换，这将会造成管道空气的温度变化以及能量的损失。此外，人们对于室内空气质量和热舒适度的要求越来越高。虽然管道换热的传热规律已经被人们所了解，但仍然有必要通过实验对管道换热的数学模型进行验证、研究和评价。本文选取了较为常用的能耗模拟软件EnergyPlus中的数学模型进行研究。

在过去几十年中，国外的许多学者从不同角度提出了许多针对管道换热的数学模型。TOBIAS[3]将拉普拉斯变换应用到提出的数学模型中，通过拉普拉斯变换能够计算出进气温度的扰动对出口温度的影响；该模型应用于模拟软件HVACSIM+中，通过将管道划分为多个部分可减少由传热系数等因素带来的误差。

GROT和HARRJE[4]基于TOBIAS模型建立了外部绝缘和内部绝缘管道的数学模型。模型中管内空气的能量变化率忽略不计，即空气的热容量忽略不计，这大大降低了两个耦合常微分方程的计算难度。

JAKOB[5]的数学模型与GROT和HARRJE[4]的数学模型相似，但是概述数学模型仅考虑管道内空气沿X轴方向的温度变化，将管道切割成若干个部分以后，假设每一个部分内部温度相同，简化了计算量。

以往文献中针对管道换热的数学模型均较为复杂，需要许多参数进行计算；能耗模拟软件EnergyPlus[6]中所采用的数学模型则相对简单，模型假设管道外部空气温度恒定，管道内外表面温度恒定且相同，管道内空气温度在X轴的每个横截面均相同。

目前，国内过于管道换热的实验和理论研究均较少。本文针对EnergyPlus中管道空气换热的数学模型的特点，并结合实际应用中的常用工况进行实验的设计。实验中保持空气流量恒定、管道外界温度恒定，同时结合实验中的实际工况进行模型的计算，重点分析了EnergyPlus数学模型在计算管道空气温度变化、空气能量损失率的变现。同时还分析了EnergyPlus中固定传热系数对于空气流量变化的实际应用中的影响。

1 EnergyPlus管道换热数学模型的计算

1.1 数学模型的介绍

首先截取管道的一个横截单元，如图1所示。该水平管道充满空气，温度沿横截面分布均匀，管壁厚度不计，假设外界温度恒定且外界温度高于管内空气温度[6-7]。

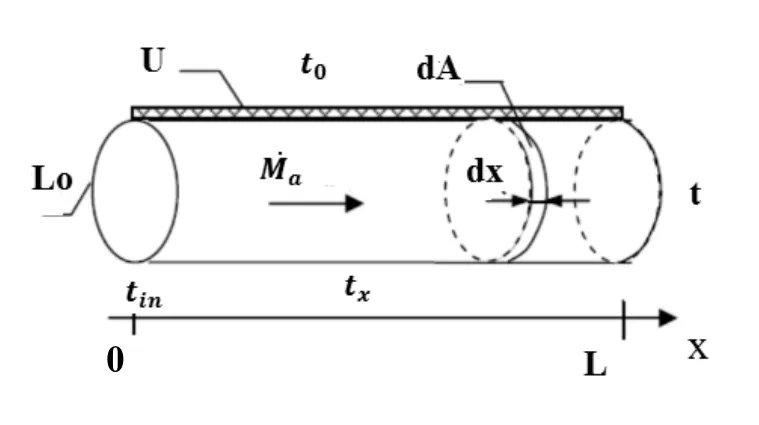
图1 水平圆管内流体流动的数学模型

对于管道内的一个微元。选取轴向作为坐标方向，列出连续性方程。假定管壁不同位置的温度相同且恒定。模型的基本方程如下所示。1）连续性方程

2）热流量的变化

3）每一个横截单元的热损失

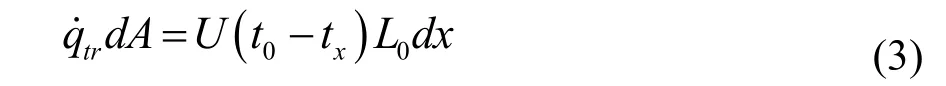
4）管内空气温度沿管道的变化

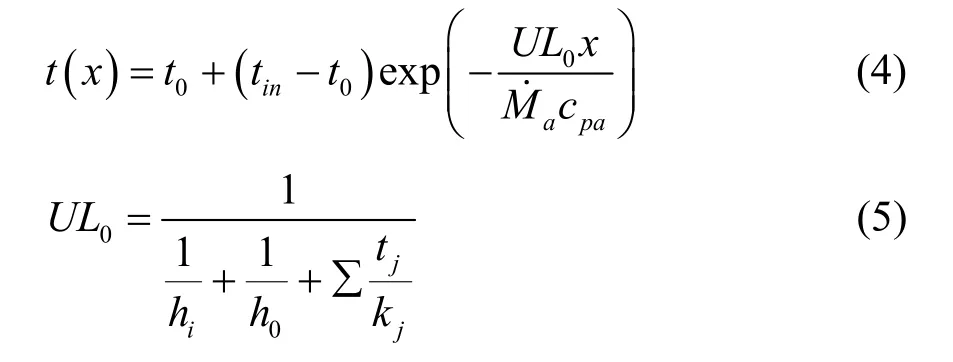
5）内部传热系数

6）雷诺数

7）能量损失率

式中：

A——横截面的面积，m2；

——空气的热容，W/K；

tx——管道内不同位置的空气，℃；

Lx——单位长度的管道面积，m；

U——热传递系数，W/(m2·K)；

t0——外界温度，℃；

tin——进气温度，℃；

tout——排气温度，℃；

——空气的质量流量，kg/s；

cpa——空气的比热容，J/(kg·K)；

hi——内部传热系数，W/(m2·K)；

h0——外部传热系数，W/(m2·K)；

tj——第j层的厚度，m；

kj——第j层的传热系数，W/(m·K)；

Nu——努塞尔数；

Re——雷诺数；

λair——空气导热系数，W/(m·K)；

Dh——管道水力直径，m；

Pr——普朗特数；

L——管道长度，m；

v——空气流动速度，m/s；

ϑ——空气运动粘度，m2/s；——能量损失率，W。

在以上方程组中，Nu、Re和Pr是3个非常重要的无量纲参数，分别反映管内空气的对流换热强烈程度、空气流动情况和空气物理性质对对流传热过程的影响。这些参数随空气物性参数不同以及流速和管壁的情况不同而改变。根据这一模型建立的方程组以及对应的无量纲化方程，可以得出管道空气温度随流速、管外温度、流动距离等因素变化而变化。

1.2 数学模型的计算

在计算过程中，方程(4)为计算管道内空气温度变化的核心公式，为了与后面实验进行对比分析，选取管道外界温度t0为实验中管道入口温度，t0为实验中的外界温度，和cpa为实验所对应的空气的质量流量和实验空气温度的比热容，其它变量也保持与实验一致。

2 实验设计及结果分析

2.1 实验设计

实验测试房间为一个长宽高分别为6.5 m、2.3 m和2.65 m的绝热房间，通入房间的管道直径为0.2 m，管壁厚度为0.9 mm，管道材料为钢，其热导率是40 W/m·K。为保持测试房间内部管道周围温度稳定均匀，实验采用地暖加热的方式，所使用的电子地暖加热片的型号是ESWA1413。在测试房间的外部，外部空气经过含有加热和冷却盘管的通风设备，加热或冷却到实验所需要的空气温度。空气通过流量阻尼器的调节而达到实验所需要的空气流量，其流量在流量压力计中显示，流量压力计的型号为KIMO CP100，其示意图如图2所示。

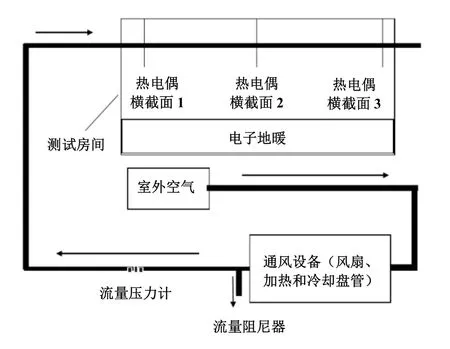
图2 实验设备示意图

在管道伸入房间的进口处、中间、出口处，分别在管道内部和管壁安装了11个T型热电偶[10]，形成了3个热电偶横截面；相邻两个横截面的间距为3 m。因此3个横截面分别可测量空气在外界温度恒定的情况下在0 m、3 m和6 m处的温度变化。热电偶在各个横截面的排布方式如图3所示。其中内部5个热电偶用来测量空气温度，管壁上的5个热电偶用来测量管壁温度。

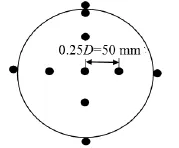
图3 热电偶在3个横截面上的分布示意图

图4 测试房间内部实物图

测试房间内部的不同位置分布了9个热电偶，用来测量管道外界的平均温度，确保管道外界温度稳定和均匀。测试房间示意图如图4所示。管道空气在距离入口3 m和6 m处的温度，从而与实验中第2个热电偶横截面和第3个热电偶横截面的平均温度进行对比。此外还可以通过计算进行能量损失率的对比。

对于稳定组1，得到实验数据后，根据式(18)可计算得到每一个横截面的平均温度的误差为±0.105 ℃，再根据式(19)可得出能量损失率的误差为±18.15 W；在与计算结果的对比中将结合误差线进行分析。温度变化与模型计算结果的对比如图5所示，可知在入口处、3 m处和6 m处，模型的计算结果均在误差允许范围之内。

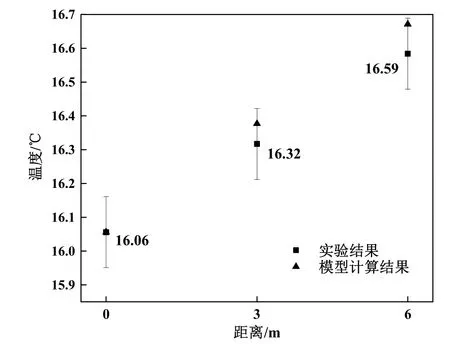
图5 稳定组1的温度变化与模型计算结果对比

能量损失率的实验结果与计算结果的对比如图6所示，图中的结果是根据入口处与6 m处的温差计算得到。由图可知，通过EnergyPlus的模型计算结果落在实验误差允许的范围内。

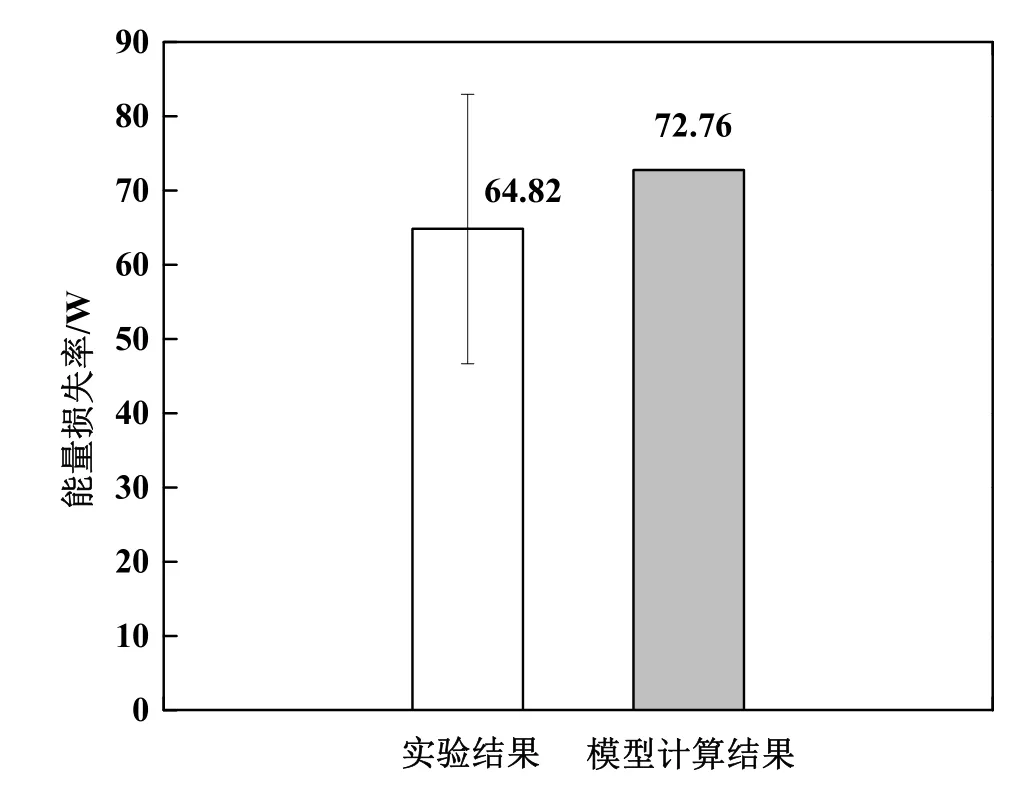
图6 稳定组1的能量损失率与模型计算结果对比

对于稳定组2，由以上同样的方法计算可知，每一个横截面的平均温度的误差为±0.106 ℃，能量损失率的误差为±17.95 W，如图7所示；EnergyPlus的计算结果在实验误差允许的范围内。

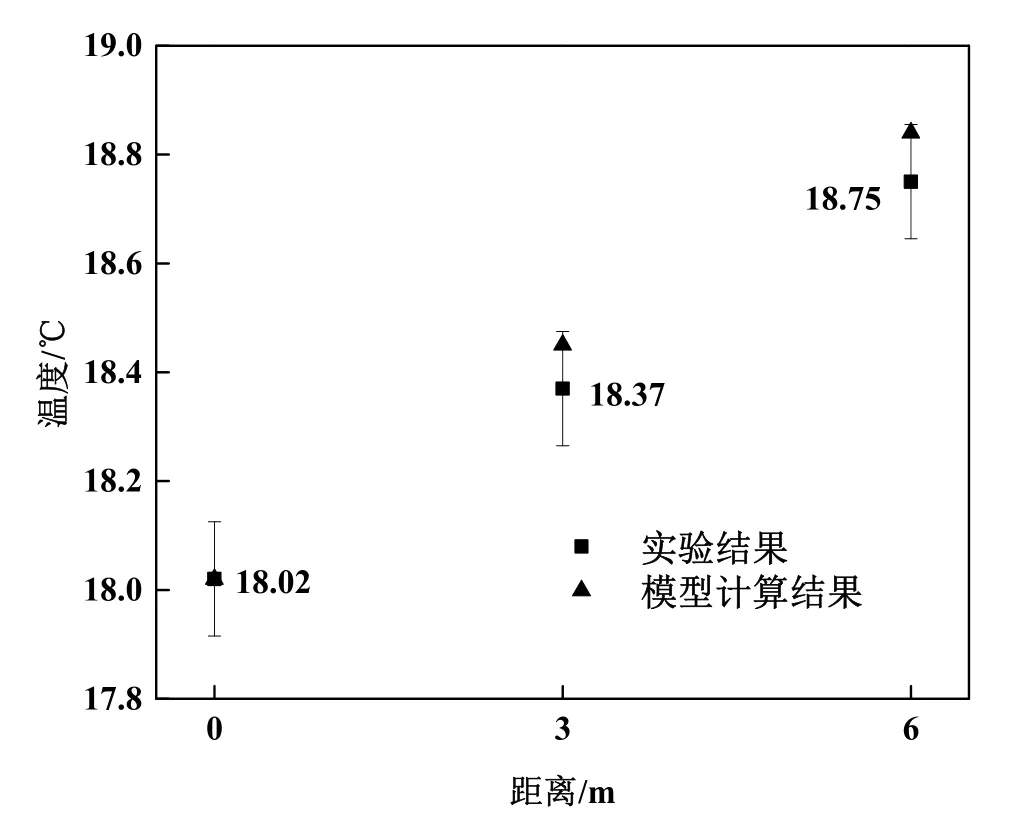
图7 稳定组2的温度变化与模型计算结果对比

能量损失率的实验结果与计算结果的对比如图8所示，图中的结果是根据入口处与6 m处的温差计算得到。由图可知，稳定组2的情况与稳定组1的情况相同，EnergyPlus的模型计算结果均在实验可接受的范围之内。

图8 稳定组2的能量损失率与模型计算结果对比

由稳定组1和稳定组2的对比分析可知，用EnergyPlus的管道数学模型来估算稳定情况（进气温度不变、外界温度不变）的管道内温度变化及能量损失率可达到预期结果。

对变化组而言，其进气温度从18.02 ℃上升至18.84 ℃再下降至18.05 ℃，此时仅研究实验中第3个热电偶横截面（6 m处）的平均温度与计算结果的对比。如图9所示，当进气温度保持在18 ℃左右的时候，EnergyPlus模型的计算结果落在误差线内；而当进气温度从上升的不稳定过程中，模型的计算结果落在误差线以外；由图中数据可看到，虽然进气温度在初始值的基础上仅仅增加了0.82 ℃，在长达10 min的过程中，模型计算结果都严重偏离了可接受的误差范围。因此，EnergyPlus的管道换气数学模型对于动态变化的工况并不适用。

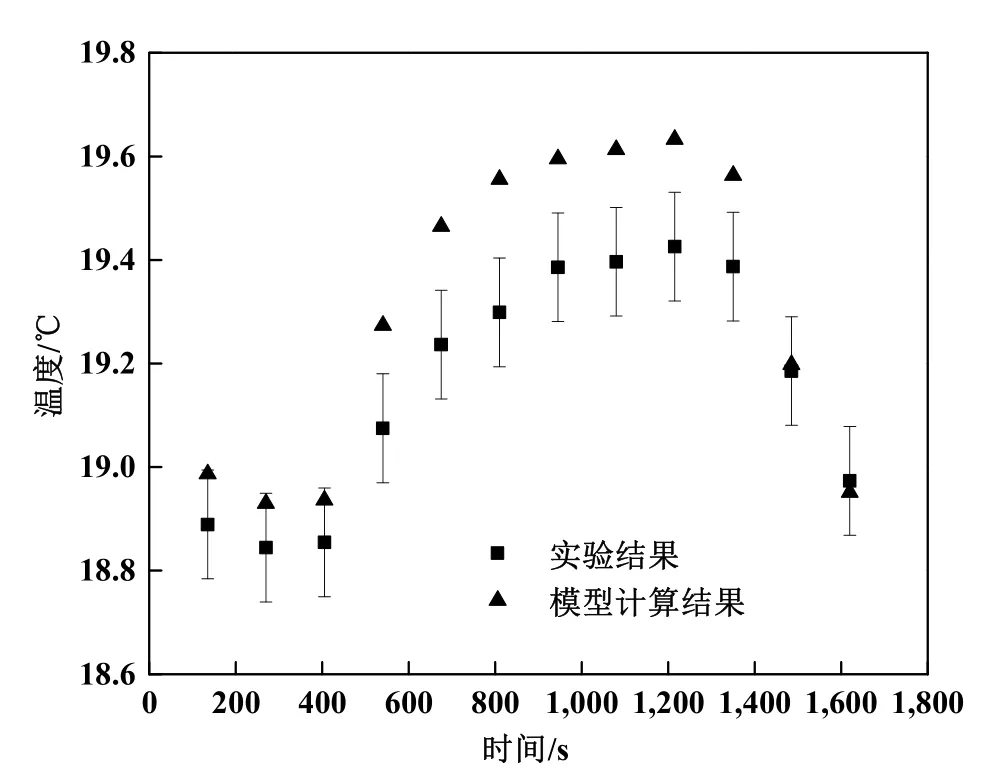
图9 变化组温度变化（6 m处）与模型计算结果对比

3 EnergyPlus中固定传热系数的影响

在EnergyPlus的使用过程中，其管道换热模块需输出固定的传热系数U；而在应用中管道空气的流量会根据实际情况出现变化，也就是传热系数U并不是完全固定的。因此，固定的传热系数U将给实际应用的模拟分析带来偏差。本文从管道空气的温度变化和管道空气的能量损失率两个方面进行分析。

3.1 固定传热系数对温度计算的影响

本文以实验中稳定组1（流量350.4 m³/h）的实验结果为基础，通过基于流量为210 m³/h、350.4 m³/h和500 m³/h的传热系数的模型计算结果与实验结果进行温度变化的比较，来分析固定传热系数对实际应用中温度计算的影响。此处对比分析的误差线仍然是±0.105 ℃。

计算结果如图10所示，可以看出当基于实验流量相同（350.4 m³/h）的传热系数进行计算时，EnergyPlus的模型计算结果落在误差允许范围内；在实际应用中，若流量不变，则可由EnergyPlus管道换热数学模型得到较好的计算结果。当基于流量210 m³/h的传热系数进行计算时，其计算结果与实验结果有一定偏差，但也落在误差允许的范围内。但是可以估计当管道距离足够长（大于6 m）其结果将落在误差范围之外。当基于流量为500 m³/h的传热系数计算时，在距离进气口6 m处，其结果落在误差线之外。

图10 稳定组1的温度变化与模型计算（基于不同流量的传热系数进行计算）结果对比

3.2 固定传热系数对能量损失率计算的影响

此处分析固定传热系数对能量损失率的影响，仍然以实验中稳定组1（流量350.4 m³/h）的实验结果为基础，通过基于流量为210 m³/h、350.4 m³/h和500 m³/h的传热系数的模型计算结果与实验结果进行能量损失率的比较，来分析固定传热系数对实际应用中的影响。此处对比分析中的误差线仍然是±18.15 W。

对比结果如图11所示，稳定组1在实验中的流量是350.4 m³/h，当模型的计算基于流量为210 m³/h和500 m³/h的传热系数时，其结果在距离入口处、6 m处的能量损失率与实验结果有一定的偏差，但都落在误差线以内；可以估计当管道距离更长的时候，基于流量为210 m³/h和500 m³/h的传热系数的能量损失率的计算值会落在误差线以外。因此，当流量偏差较大或管道距离较长时，EnergyPlus中固定的传热系数U会给实际应用的能量损失率的模拟计算带来偏差。

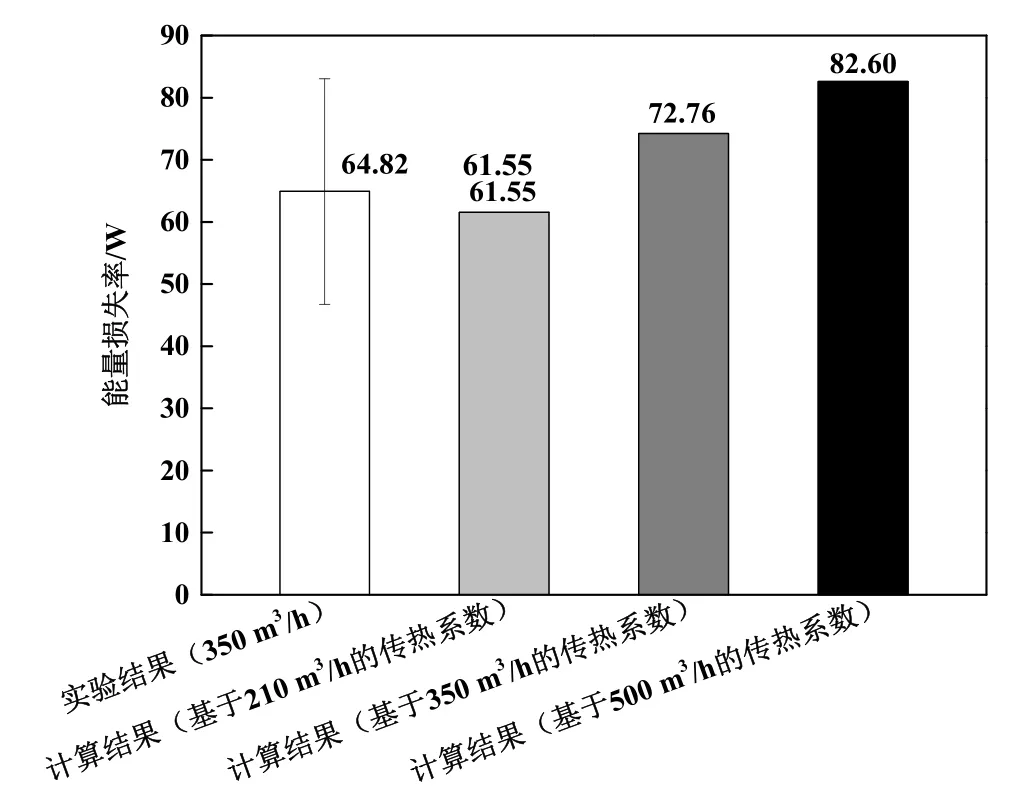
图11 稳定组1的能量损失率实验值与模型计算（基于不同流量的传热系数进行计算）结果对比

4 结论

本文通过对EnergyPlus管道换热数学模型的研究，设计了验证性的实验，根据实验工况进行了管道换热数学模型的计算，并通过实验误差的分析；将实验结果与模型计算结果进行对比，研究在稳定工况和变化工况下管道空气温度的变化和能量损失率实验结果与模型计算结果的差别。同时本文还基于实验中的稳定工况组，分析了EnergyPlus中输入固定传热系数对于实际应用的影响，并得出以下结论。

1）对于外界温度稳定、进气温度稳定、管道空气流量稳定的工况计算，EnergyPlus的管道换热模型表现较好，温度变化与能量损失率的计算结果都在实验误差所接受的范围之内。因此在实际运用中，对于稳定工况的管道换热的计算，可选用EnergyPlus来进行模拟。

2）对于进气温度变化的工况，EnergyPlus管道换热模型的计算结果与实验结果偏差较大，当温度升高时，模型的计算结果均落在实验误差允许的范围之外。因此在实际应用中，进气温度变化的工况不适合用EnergyPlus进行模拟计算。

3）EnergyPlus管道换热模块使用过程中需输入固定传热系数的特点，在实际应用中，将对管道空气温度和能量损失率的计算带来偏差。当流量变化时，部分结果落在误差允许范围之外；当实际流量与输入EnergyPlus的流量存在偏差，随着管道长度的增加，EnergyPlus得出的出口处空气温度和能量损失率计算结果的误差也会增加。因此，这是EnergyPlus管道换热数学模型在实际应用中的局限性。

[1] 李峥嵘, 于雅泽, 黄俊鹏. 浅析建筑节能政策[J]. 制冷技术, 2004, 24(2): 14-16.

[2] 张欢, 陈汝东. 直埋敷设冷水管道的保温性能分析[J].制冷技术, 2009, 29(3): 53-56.

[3] TOBIAS J R. Simplified transfer function for temperature response of fluids flowing through coils, pipes or ducts[J]. ASHRAE Transactions, 1973, 79(1): 19-22.

[4] GROT R A, HARRJE D T. The transient performance of a forced warm air duct system[J]. ASHRAE Transactions, 1981, 88: 3-12.

[5] JAKOB F E, FISCHER R D, FLANIGAN L J. Experimental validation of the duct submodel for the SP43 simulation model[J]. ASHRAE Transactions, 1987, 93: 1499-1514.

[6] MARIPUU M L. Demand Controlled Ventilation (DCV) Systems in Commercial Buildings. Functional Requirements on Systems and Components[M]. Goteborg: Chalmers University of Technology, 2009.

[7] 王玲. 工业管线现场节能评价管道模型装置设计[J].机电工程技术, 2014(8): 73-76.

[8] Data Sheet. NI 9211 Thermocouple Input Module. National Instruments[EB/OL]. (2012-07-03). http://sine. ni.com/nips/cds/view/p/lang/en/nid/202554.

[9] Data sheet. CP 100 Pressure transmitter[EB/OL]. (2014-02-09). http://www.kimo.fr.

[10] 张丽. 热电偶的选型及误差分析[J]. 科学之友, 2012(15): 152-153.

[11] 李潮锐, 郑碧华. 实验误差分析中的概念及意义[J].中山大学学报(自然科学版), 2003, 42(S1): 150-153.

[12] MOFFAT R J. Describing the uncertainties in experimental results[J]. Experimental Thermal and Fluid Science, 1988, 1(1): 3-17.

[13] MOFFAT R J. Using uncertainty analysis in the planning of an experiment[J]. Journal of Fluids Engineering, 1985, 107(2): 173-178.

[14] 何小渝. 用排气管道量热器法测试制冷压缩机制冷量时的误差分析及其结果应用[J]. 制冷技术, 1989, 9(2): 28-28.

[15] 张蕾. 微通道换热器空调系统性能试验分析[J]. 制冷技术, 2010, 30(1): 33-36.

Analysis of Mathematical Models of Ventilation Ducts in EnergyPlus

PENG Ji*1, WANG Ruzhu1, NOVAKOVIC Vojislav2
(1-Institute of Refrigeration and Cryogenics, Shanghai Jiao Tong University (SJTU), Shanghai 200240, China; 2-Norwegian University of Science and Technology (NTNU), KolbjornHejesvei 1B, Trondheim, NO-7491, Norway)

Calculation of heat transfer in ventilation ducts is conducted based on mathematical models in EnergyPlus with different conditions. Experiment focused on air temperature change and energy loss rate in ducts is made with the same conditions as well. And the quantitative analysis of mathematical models in EnergyPlus is studied. Aiming at the characteristic of using fixed U-value in EnergyPlus, the correlative calculation and analysis are conducted. The results show that the differences between the calculation results and the measurement results for the temperature variation and the heat loss power are very small and can be accepted when the conditions are quite stable. However, when it comes to the unstable state, the differences between the calculation results and measurement results are very large. And the fixed U-value required by EnergyPlus is easy to bring large errors when the mathematical model is applied in practice.

EnergyPlus; Ventilation system; Heat transfer in ducts; Heat loss; Mathematical model; Fixed U-value

10.3969/j.issn.2095-4468.2017.01.101

*彭吉（1991-），男，硕士研究生。研究方向：建筑节能。联系地址：上海市闵行区东川路800号，邮编：200240。联系电话：021-34206548。E-mail：rzwang@sjtu.edu.cn。