考虑决策者行为的新产品开发方案选择方法*
2017-04-19樊治平沈阳工业大学管理学院机械工程学院沈阳110870东北大学工商管理学院沈阳110169
于 超, 樊治平(1. 沈阳工业大学 a. 管理学院, b. 机械工程学院, 沈阳 110870; . 东北大学 工商管理学院, 沈阳 110169)
考虑决策者行为的新产品开发方案选择方法*
于 超1,2, 樊治平2
(1. 沈阳工业大学 a. 管理学院, b. 机械工程学院, 沈阳 110870; 2. 东北大学 工商管理学院, 沈阳 110169)
针对新产品开发方案选择问题,提出一种决策分析方法。在该方法中,以原产品成熟期的利润为参考点,基于前景理论,计算新产品研发成功情景下预期利润增量的前景价值和新产品研发失败情景下预期损失的前景价值,进一步地计算二者的决策权重,在此基础上计算各方案的综合前景值并对方案进行排序。最后,通过一个算例对本文提出方法的实用性进行验证。
新产品开发; 决策者行为; 前景理论; 前景值; 方案选择
企业为了提升其在市场中的竞争力以更好地占有市场,通常十分重视新产品开发,在新产品开发过程中,新产品开发方案的选择至关重要[1-2]。一般来说,产品的生命周期由导入期、成长期、成熟期和衰退期四个阶段构成[3],企业通常会在产品进入成熟期后选择研发新产品,包括研发全新型新产品和改进型新产品,以便在该产品进入衰退期后有新产品继续占有市场,带来销售增量。在选择新产品开发方案之前,企业决策者会综合评估各方案研发成功和研发失败的概率以及各方案的预期收益,当方案的预期收益超过参照收益(参考点)时,决策者会感到欣喜,反之,决策者会感到失望。决策者欣喜和失望的心理感知可被视为决策者的潜在心理行为,决策者的这种潜在心理行为会在感知层面上影响决策者对方案的满意程度,进而影响其对方案的选择。因此,有必要研究考虑决策者这种潜在心理行为的新产品开发方案的选择方法。
近年来,关于考虑决策者行为的新产品开发方案选择问题,有学者先后展开了研究并取得了一定的研究成果。徐皓等[4]针对新产品开发方案选择方法进行了研究,考虑了决策者给出指标期望的情形,给出了一种决策分析方法;姜艳萍和程树磊[5]针对新产品开发方案选择问题进行了研究,考虑了竞争产品方案的评价信息,提出了一种基于前景理论的新产品开发方案选择方法;Yan等[6]提出了一种考虑行为的模糊目标导向的决策分析方法,将提出的方法应用于新产品开发方案选择问题;Lin等[7]针对新产品开发问题进行了研究,通过消费者导向实验获取顾客的偏好信息,提出了一种以顾客偏好为导向的决策支持方法;于超和樊治平[8]对决策者在新产品开发方案选择过程中表现出的失望规避的行为特征进行了描述,进而提出了一种考虑决策者失望规避的新产品开发方案选择方法。但在现实中,新产品研发成功与否是不确定的,决策者在不确定的情况下往往会表现出参照依赖、损失规避等行为特征,而如何考虑决策者的这些心理行为进而辅助决策者选择出令其感到最为满意的新产品开发方案,有关研究还不多见。鉴于此,本文提出一种考虑决策者行为的新产品开发方案选择方法。
一、问题描述
下面给出本文关注问题中所涉及的集和量的描述。
Ai:第i个方案(即新产品开发方案),i∈M,M={1,2,…,m}。
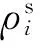
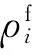
q:原产品(即当前出售的产品)的销售量,这里的销售量是指原产品在某指定时间段内的销售量。
p:原产品的单价。
c:原产品的单位可变成本。
cF:原产品的固定成本,这里的固定成本是指原产品在某指定时间段内的固定成本。
pi:方案Ai拟定的新产品单价,i∈M。
Δqi:在方案Ai研发成功的情况下,其对应的产品投放市场后预计可能带来的销售增量,i∈M。qi的值可由专家进行预测。
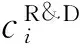
ci:方案Ai的单位可变成本,i∈M。

通常,方案的研发风险越大,研发成功的概率就越小,与此同时,对应的研发费用也会较高[9]。这类新产品开发方案若研发成功带来的利润较高,但若研发失败则会造成较大的损失。本文要解决的问题即综合考虑新产品开发方案可能带来的预期利润以及决策者的心理感知,依据A、ρ、q、p、c等相关决策信息选择适合的新产品开发方案。
二、原理与方法
考虑决策者行为的新产品开发方案选择方法如下:
首先,计算新产品的预期利润增量与预期损失。这里假定:若选定的新产品研发成功,则该新产品推入市场后会在未来的一段时期内取得一定的销售增量,并且在这种情景下企业将停止生产和销售原产品;若选定的新产品研发失败,则企业保持原产品的生产与销售不变,前期投入的研发成本全部损失。这里选择原产品成熟期的利润作为参考点,则新产品研发成功情景的预期利润增量可被视为相对于参考点的收益,而新产品研发失败情景的预期损失可被视为相对于参考点的损失。若新产品开发方案Ai研发成功,则将其指定时间段内的预期利润增量记为gi,计算公式为
[q(p-c)-cF] (i∈M)
(1)
若新产品开发方案Ai研发失败,则将其指定时间段内的预期损失记为li,计算公式为
(2)
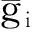
(3)
(4)


(5)
(6)
式中:0≤α≤1,0≤β≤1;λ>1[10-11]。通常,参数α、β和λ的值可通过实验方法来确定[11,12-14]。
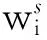
(7)
(8)
式中:γ>0;δ>0[11]。通常,参数γ和δ的值可通过实验方法来确定[11,12-14]。
最后,计算方案的综合前景值。记ui表示方案Ai的综合前景值,计算公式为
(9)
可见,新产品开发方案的综合前景值ui越大,方案Ai越好。依据ui值的大小,可以对所有方案进行排序或选择最好的方案。
综上,新产品开发方案选择方法的计算步骤如下:
步骤1 根据式(1)和式(2),计算gi和li,i∈M。
步骤5 根据式(9),计算ui,i∈M。
步骤6 依据ui值的大小,确定方案排序。
三、算例
本部分以GL公司新款变频空调开发方案选择问题为例来说明上文提出方法的潜在应用价值。
GL公司是一家空调生产企业,KFR-50LW/(50568)FNEa-4是该公司推出的一款很受欢迎的2匹立柜式变频系列家用冷暖空调,该产品曾成功地占据一定的市场份额。然而,由于相关环保标准的提升以及消费者对于柜式空调需求的提高,GL公司的这款柜式空调产品已经进入了成熟期。为了保证市场占有率并争取更大的利润,GL公司决定以原产品为基础研发改进型新产品,推出一款性能更优的立柜式空调,预计新款的立柜式空调在噪音控制性能方面会有显著提升。若新款立柜式空调研发成功,则代替原产品;否则,将继续维持原产品的生产与销售。该公司现有的KFR-50LW/(50568)FNEa-4款立柜式空调的内机噪音和外机噪音最高分别为43分贝和54分贝,成熟期的年销售量为4.3万台,市场单价为5 480元/台,单位变动成本为910元/台,年固定成本为500万元。针对新款立柜式空调的设计,该公司的研发团队给出了5种备选方案,即A1、A2、A3、A4和A5。
A1:改变底座设计,预计内机噪音控制在43分贝以内,外机噪音控制在53分贝以内。
A2:减少压缩机封闭区开孔面积,预计内机噪音控制在42分贝以内,外机噪音控制在53分贝以内。
A3:改进吸排气管,在振动较大位置增加减震块,预计内机噪音控制在40分贝以内,外机噪音控制在53分贝以内。
A4:改选噪音指标低的压缩机,预计内机噪音控制在39分贝以内,外机噪音控制在52分贝以内。
A5:对风机的结构加以改造,预计内机噪音控制在39分贝以内,外机噪音控制在50分贝以内。
研发团队对每个方案研发成功的概率、对应的研发成本、研发成功的情况下预计一年内新产品带来的销售增量以及新产品的单价、单位变动成本和年固定成本多项指标进行了估计与制定,具体如表1所示。

表1 新产品开发备选方案对应各项指标的取值 元
运用上文提出方法进行求解的部分计算过程和结果如下:
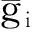
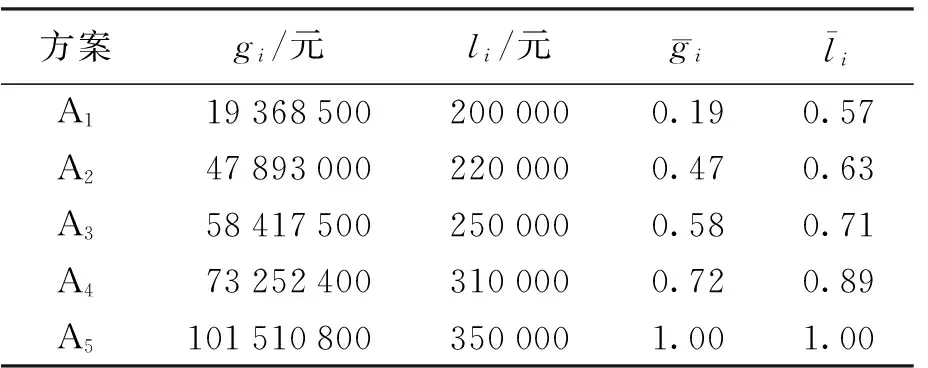
方案gi/元li/元 gi liA1193685002000000.190.57A2478930002200000.470.63A3584175002500000.580.71A4732524003100000.720.89A51015108003500001.001.00
通常,前景理论中参数α、β、λ、γ和δ的值可通过实验方法来确定[11,12-14],例如,Tversky和Kahneman在文献[10]中通过实验的方法给出的参数取值为:α=β=0.88、λ=2.25、γ=0.61和δ=0.69。从已有研究成果来看,许多学者在他们的研究中直接引用了Tversky和Kahneman给出的参数取值[5,15-16],但也有一些学者针对不同实际背景的问题研究得到的参数[12-14,17-20]与Tversky和Kahneman给出的参数取值相近,如Xu等[20]进行考虑旅行者行为的路径选择问题研究,通过实验方法确定的参数取值为:α=0.37、β=0.59、λ=1.51和γ=δ=0.74。在本文中,考虑到参数确定需要大量的工作,限于篇幅直接采用Tversky和Kahneman给出的参数取值。
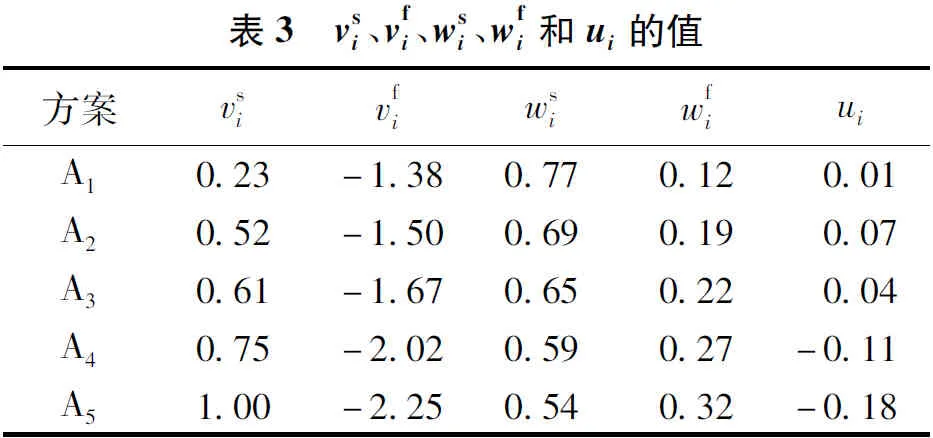
方案vsivfiwsiwfiuiA10.23-1.380.770.120.01A20.52-1.500.690.190.07A30.61-1.670.650.220.04A40.75-2.020.590.27-0.11A51.00-2.250.540.32-0.18
由表3可知,方案的排序结果为A2≻A3≻A1≻A4≻A5,即决策者可考虑将新产品开发方案A2作为最终选择。
为了进一步验证模型参数取值的变化对决策结果的影响,这里选择了6种具有代表性的参数取值,分别计算各方案相应的综合前景值,并得到方案的排序结果,具体如表4所示。
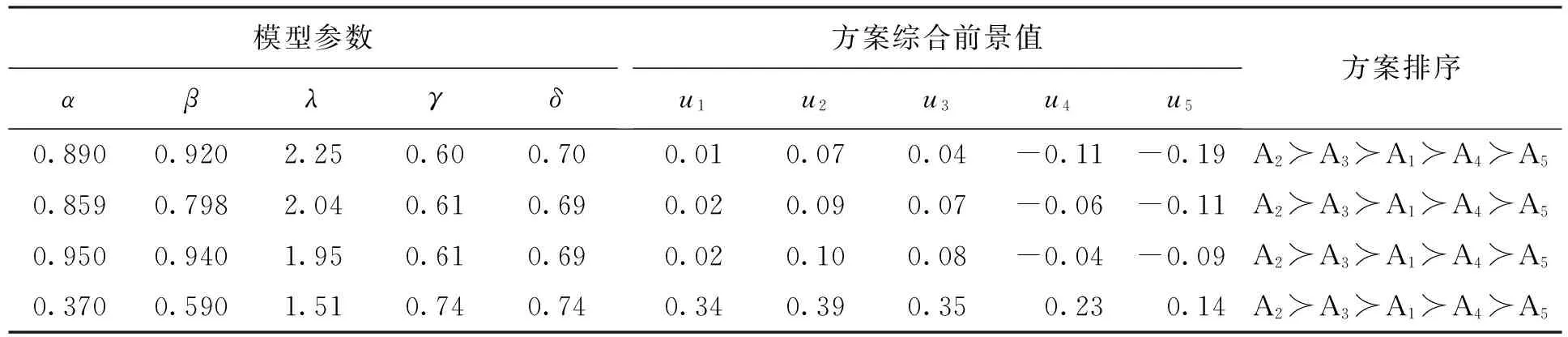
表4 针对6种代表性参数取值的方案综合前景值和方案排序结果
这里需要对这6种代表性参数取值的选取来源给出简单的说明:参数α=0.890、β=0.920、λ=2.25源自文献[12]的实验值;参数α=0.859、β=0.798、λ=2.04源自文献[13]的实验值;参数α=0.950、β=0.940、λ=1.95源自文献[14]的实验值;参数α=0.370、β=0.590、λ=1.51源自文献[20]的实验值;参数γ=0.60、δ=0.70源自文献[12]的实验值;参数γ=0.61、δ=0.69源自文献[11]的实验值;参数γ=0.74、δ=0.74源自文献[20]的实验值。
将表4中的方案排序结果与算例中的方案排序结果进行对比,易知方案排序结果相对稳定。为了进一步说明本文的方法,这里将本文提出的方法与已有研究方法进行比较。若不考虑决策者的心理行为因素,则此类问题便退化为传统的风险决策问题,计算得到各方案的损益值分别为0.15,0.34,0.38,0.37和0.42,进而得到方案排序结果为A5≻A3≻A4≻A2≻A1,即新产品开发方案A5可作为满意的方案。易知,本文提出的方法与传统的风险决策方法相比,得到的方案排序结果不同,这说明在考虑决策者参照依赖、损失规避等心理行为的情形下,方案的排序结果会发生变化。
四、结 语
本文给出了一种考虑决策者行为的新产品开发方案选择方法。该方法考虑了决策者的参照依赖、损失规避等行为因素,给出了一种基于前景理论的决策分析方法。本文的方法为解决现实中的新产品开发方案选择问题提供了一种新途径。
[1]汪勇,徐琼,李云梅,等.新产品开发立项决策流程优化方法及应用研究 [J].科技进步与对策,2014,31(20):64-68.
[2]李丹,张超.新工业革命下我国制造业发展路径分析 [J].沈阳工业大学学报(社会科学版),2016,9(3):198-201.
[3]Dean J.Pricing policies for new products [J].Harvard Business Review,1950,28(6):45-53.
[4]徐皓,樊治平,刘洋,等.一种考虑指标期望的产品设计方案选择方法 [J].工业工程与管理,2010,15(1):32-36.
[5]姜艳萍,程树磊.基于前景理论的新产品开发方案选择方法 [J].管理学报,2012,9(5):767-771.
[6]Yan H B,Huynh V N,Ma T,et al.Non-additive multi-attribute fuzzy target-oriented decision analysis [J].Information Sciences,2013,240(10):21-44.
[7]Lin Y C,Chen C C,Yeh C H.Intelligent decision support for new product development:a consumer oriented approach [J].Applied Mathematics & Informa-tion Sciences,2014,8(6):2761-2768.
[8]于超,樊治平.考虑决策者失望规避的新产品开发方案选择方法 [J].工业工程与管理,2015(6):54-60.
[9]Tishler A.How risky should an R&D program be? [J].Economics Letters,2008,99(2):268-271.
[10]Kahneman D,Tversky A.Prospect theory:an analysis of decision under risk [J].Econometrica:Journal of the Econometric Society,1979,47(2):263-291.
[11]Tversky A,Kahneman D.Advances in prospect theory:cumulative representation of uncertainty [J].Journal of Risk and Uncertainty,1992,5(4):297-323.
[12]Abdellaoui M.Parameter-free elicitation of utility and probability weighting functions [J].Management Science,2000,46(11):1497-1512.
[13]Abdellaoui M,Bleichrodt H,Paraschiv C.Loss aversion under prospect theory:a parameter-free measurement [J].Management Science,2007,53(10):1659-1674.
[14]Booij A S,Kuilen G.A parameter-free analysis of the utility of money for the general population under prospect theory [J].Journal of Economic Psychology,2009,30(4):651-666.
[15]Birnbaum M H.Three new tests of independence that differentiate models of risky decision making [J].Management Science,2005,51(9):1346-1358.
[16]He X D,Zhou X Y.Portfolio choice under cumulative prospect theory:an analytical treatment [J].Management Science,2011,57(2):315-331.
[17]Wu G,Gonzalez R.Curvature of the probability weighting function [J].Management Science,1996,42(12):1676-1690.
[18]Bleichrodt H,Pinto J L.A parameter-free elicitation of the probability weighting function in medical decision analysis [J].Management Science,2000,46(11):1485-1496.
[19]Prelec D.Compound invariant weighting functions in prospect theory [M].Cambridge:Cambridge University Press,2000:45-51.
[20]Xu H,Zhou J,Xu W.A decision-making rule for modeling travelers’ route choice behavior based on cumulative prospect theory [J].Transportation Research Part C:Emerging Technologies,2011,19(2):218-228.
(责任编辑:张 璐)
Alternative selection method for new product development
considering behavior of decision makers
YU Chao1,2, FAN Zhi-ping2
(1a. School of Management, 1b. School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870, China; 2. School of Business Administration, Northeastern University, Shenyang 110169, China)
Aiming at the selection of new product development plan, a method of decision analysis is proposed. In this method, the profit of existing products in the mature period is regarded as the reference point. Base on prospect theory, the prospect values of the expected profit increment in the success scenario and the expected loss in the failure scenario of new product development are calculated, and the corresponding weights are calculated. Based on that, the overall prospect value of each alternative is calculated and the ranking of alternatives is determined. Finally, the practicality of the proposed method is illustrated through an example.
new product development; behavior of decision maker; prospect theory; prospect value; plan selection
2016-10-25
国家自然科学基金项目(71271051)。
于 超(1987-),女,辽宁沈阳人,讲师,博士,主要从事运作管理与决策分析等方面的研究。
14∶35在中国知网优先数字出版。
http:∥www.cnki.net/kcms/detail/21.1558.C.20170330.1435.036.html
10.7688/j.issn.1674-0823.2017.02.07
C 934
A
1674-0823(2017)02-0134-05
