不同动态水压模式下迷宫流道内颗粒物运动特性研究

郑 超 吴普特, 张 林, 朱德兰 赵 笑 安伯达

(1.西北农林科技大学水土保持研究所， 陕西杨凌 712100；2.西北农林科技大学中国旱区节水农业研究院， 陕西杨凌 712100)

不同动态水压模式下迷宫流道内颗粒物运动特性研究

郑 超1吴普特1,2张 林1,2朱德兰2赵 笑2安伯达2

(1.西北农林科技大学水土保持研究所， 陕西杨凌 712100；2.西北农林科技大学中国旱区节水农业研究院， 陕西杨凌 712100)

采用PTV技术，观测三角函数、三角、台阶、矩形波形动态水压模式下迷宫流道内颗粒物的运动情况，分析不同动态水压模式下迷宫流道内单个颗粒物运动轨迹、运动速度及流体流场，揭示动态水压抗堵塞机理。结果表明：相对于三角、台阶及矩形波形动态水压模式，三角函数波形动态水压模式下颗粒物滞留滞止区内的时间最短，颗粒物的沉积概率最小，水流对颗粒物的输移能力最大；三角函数波形动态水压模式下流道内产生的水流波动效应不断冲击流道滞止区内存在的低速漩涡，加剧了滞止区水流紊动，进入滞止区的颗粒物随水流不断运动，并对滞留甚至沉积在滞止区内的颗粒物发生强烈冲击，使得颗粒物离底悬浮，返回主流区，并迅速通过流道，增大了水流对颗粒物的输移能力，增强了流道的抗堵塞性能。

动态水压； 迷宫流道； 颗粒物； 运动速度； 运动轨迹

引言

图2 迷宫流道灌水器及有机玻璃试验样件Fig.2 Schematics of labyrinth channel emitter and specimen

迷宫流道灌水器内流道结构复杂、尺寸微小(1 mm左右)，即使是水质良好且有较完备过滤措施的滴灌系统，仍有微小的固体颗粒物进入灌水器流道造成灌水器堵塞[1-4]。解决迷宫流道灌水器堵塞问题的关键是使灌水器流道具有较高的抗堵塞性能[5]。因此，众多学者常通过优选流道结构参数及优化设计流道边界，来保证流道内具有良好的流动状态，提升流道内水流对颗粒物的输移能力，进而达到提高流道抗堵塞能力的目的[6-12]。魏正英等[6]分析了迷宫流道内部流动场的情况及其堵塞机理，提出了迷宫流道主航道抗堵优化设计方法。芦刚等[7]通过两相流数值模拟，分析了灌水器内水流的流场、固相物的运动轨迹及密度分布，通过短周期抗堵塞试验，对3种涡体流道进行了短周期堵塞测试，并结合快速原形/快速制模(RP/RT)技术，提出了一种灌水器快速低成本开发的方法。喻黎明等[8]分析了梯形流道内含沙量分布及水沙流速分布，并以某一含沙量分布线作为流道边界，对流道进行优化，由此获得抗堵塞性能较好的流道模型。但由于流道边界条件及灌溉水质状况复杂，使得灌水器物理堵塞问题仍未完全被解决。近年来，为提高滴灌系统及灌水器的抗堵塞性能，有学者尝试提出动态水压滴灌系统，这种方法有别于已有的脉冲式滴灌方式[13-14]，它通过动态的工作水压加剧系统和灌水器内水流紊动，提高水流对颗粒物的输移能力，从而达到改善系统和灌水器抗堵性能的目的[15-17]。王聪[16]分析了水压模式、波动周期及振幅等波动参数对灌水器流量、均匀度和堵塞率的影响规律，得出随着动态水压波幅的增大，4种水压模式产生的波动效应逐渐减弱，波幅为2～3 m时波动效应效果最好。刘洁等[17]通过正交压力流量测试试验，分析了基础水压、波幅及波动周期等波动参数对灌水器水力性能的影响，得出基础水压对灌水器流量影响最大。这些研究主要集中于灌水器宏观水力特性方面，较少涉及灌水器流道内颗粒物运动情况及流场分析，动态水压抗堵塞机理尚不清楚。

本文通过在水源中添加一定浓度的固体颗粒物，并采用高速摄像仪分别对4种典型的动态水压模式(三角函数、三角、台阶及矩形波形)下灌水器流道内颗粒物运动情况进行连续拍摄，以获得颗粒物的运动轨迹和速度等信息，进而对比分析不同动态水压模式下迷宫流道内的颗粒物运动特性，揭示动态水压抗堵塞机理，并优选能最有效提高流道抗堵性能的动态水压模式。

1 材料与方法

1.1 试验材料

本研究选取常用的锯齿型迷宫流道结构形式(以杨凌秦川节水灌溉设备工程有限公司生产的内镶贴片式滴灌带中灌水器迷宫流道为原型，其额定流量为2 L/h)进行水流运动特性研究，流道结构及参数详见图1。为了便于观测流道内水流的运动情况，利用数控激光加工机床雕刻技术(雕刻精度为0.01 mm，表面粗糙度Ra≤0.25 μm)将平角齿形流道按1∶1的比例雕刻在透明的1 mm厚的有机玻璃板上，采用2块3 mm厚的透光性好的有机玻璃板将流道密封，并采用8个螺栓加以固定，制成试验样件，如图2所示。流道共13个单元，总长22.1 mm，流道宽度0.802 3 mm，齿高1 mm，流道深度1 mm，流道进出口平直流道加长，以便流体充分发展。在流道进口前4 mm处刻有测压孔，并通过直径2 mm的不锈钢管及透明软管连接压力传感器，以此达到实时监测流道进口压力变化的目的。

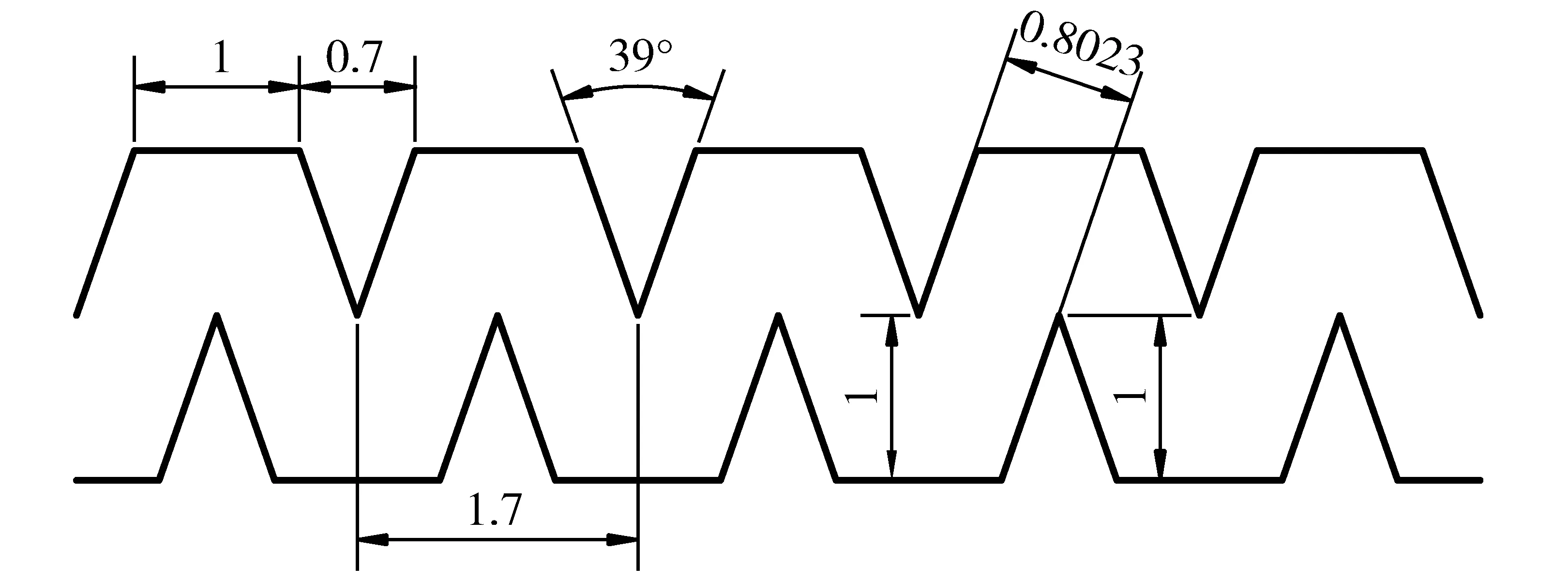
图1 迷宫流道结构及参数(单位：mm)Fig.1 Form and structure parameters of labyrinth channel

1.2 试验装置与方法

试验在西北农林科技大学中国旱区节水农业研究院灌溉水力学试验厅进行，试验装置如图3所示，主要由水箱、搅拌机(电动机转速为900 r/min)、50WBZS15-22型不锈钢自吸式耐腐蚀微型电泵、筛网过滤器(筛网孔径为0.125 mm)、变频柜、压力表(量程40 m，精度0.5%)、压力传感器(西安新敏CYB型，量程40 m，精度0.1%)、数据采集器和PTV可视化试验平台(由不锈钢支架、连续光源、高速摄像仪及VS-M0910型放大镜组成)等组成。试验采用的高速摄像仪每秒可采集0～200 000帧图像，能清晰地捕捉到粒子在微小迷宫流道内的运动情况，利用后处理软件Movias Pro Viewer 1.63可获得粒子运动轨迹及瞬时速度等运动特征参数。试验不同的动态水压模式通过变频柜控制加压水泵电机的转速来实现。采用水流跟随性较好、密度接近于水的Nylon粒子(粒径为4 μm，密度为1.04 g/cm3)作为固体悬浮颗粒物。

图3 迷宫流道颗粒物运动特性试验装置Fig.3 Schematic of test system for particles movement characteristics of labyrinth channel1.不锈钢离心泵 2.阀门 3.过滤器 4.水箱 5.搅拌机 6.压力表 7.高速摄像仪 8.变频柜 9.压力采集器 10.塑料量杯 11.试验样件 12.连续光源 13.压力传感器

试验时，在水箱中加入浓度为0.01 g/L的固体颗粒物，开启搅拌器进行搅拌，使得颗粒物均匀分布于水箱的水体中；开启变频柜并设置变频器运行参数，然后开启水泵。调节完毕后，待压力稳定，通过连接在流道进口处的压力传感器测量流道进口压力并由计算机记录压力传感器瞬时采集(1次/s)的数据，用称量法(测量2次，每次测量时间为20 min，取平均值)测量并记录流道末端出流量。开启连续光源及高速摄像仪，调整并设定高速摄像仪的焦距、数字式位移、快门速度及每秒采集帧数等参数，最后开始采集并保存高速摄像仪拍摄的图像。采集图像时，设定每秒采集6 000帧图像，快门速度、数字移动及触发模式等参数采用系统默认值。考虑到高速摄像仪观测区域有限，无法观测整个迷宫流道。因此，本研究选取位于迷宫流道中后部且流体发展充分的第7和第8流道单元作为主要的PTV观测区域，其观测区域长度为5.63 mm。

参照文献[18]，对恒定水压下流道压力流量关系进行测定，得到流道的压力流量计算公式为q=1.153H0.534(q为流道出流量，L/h；H为流道进口平均工作压力水头，m)。为了分析不同动态水压模式下迷宫流道出流量的变化，对三角函数波形、三角波形、矩形波形及台阶波形4种动态水压模式(不同动态水压模式下实测工作压力水头变化见图4)下波动周期T为30 s、振幅为3 m及流道进口基础压力水头(流道进口平均工作压力水头)为4、6、8、10、12 m时迷宫流道出流量进行测定，结果表明相比恒定水压，4种动态水压模式下流道内流量未出现明显下降，动态水压对滴灌系统的供水能力影响较小。低压灌溉是当代滴灌发展的趋势，滴灌系统工作压力的降低虽然降低了滴灌系统的实施及运行成本，但在低压条件下滴灌灌水器流道更加容易发生堵塞。因此，在PTV观测试验时选定三角函数波形、三角波形、矩形波形及台阶波形4种动态水压模式，选定较低的工作压力水头(4 m)作为流道进口基础压力水头，波动周期T和振幅分别设为30 s和3 m，共4个试验处理。

2 结果与分析

2.1 不同动态水压模式下颗粒物运动速度

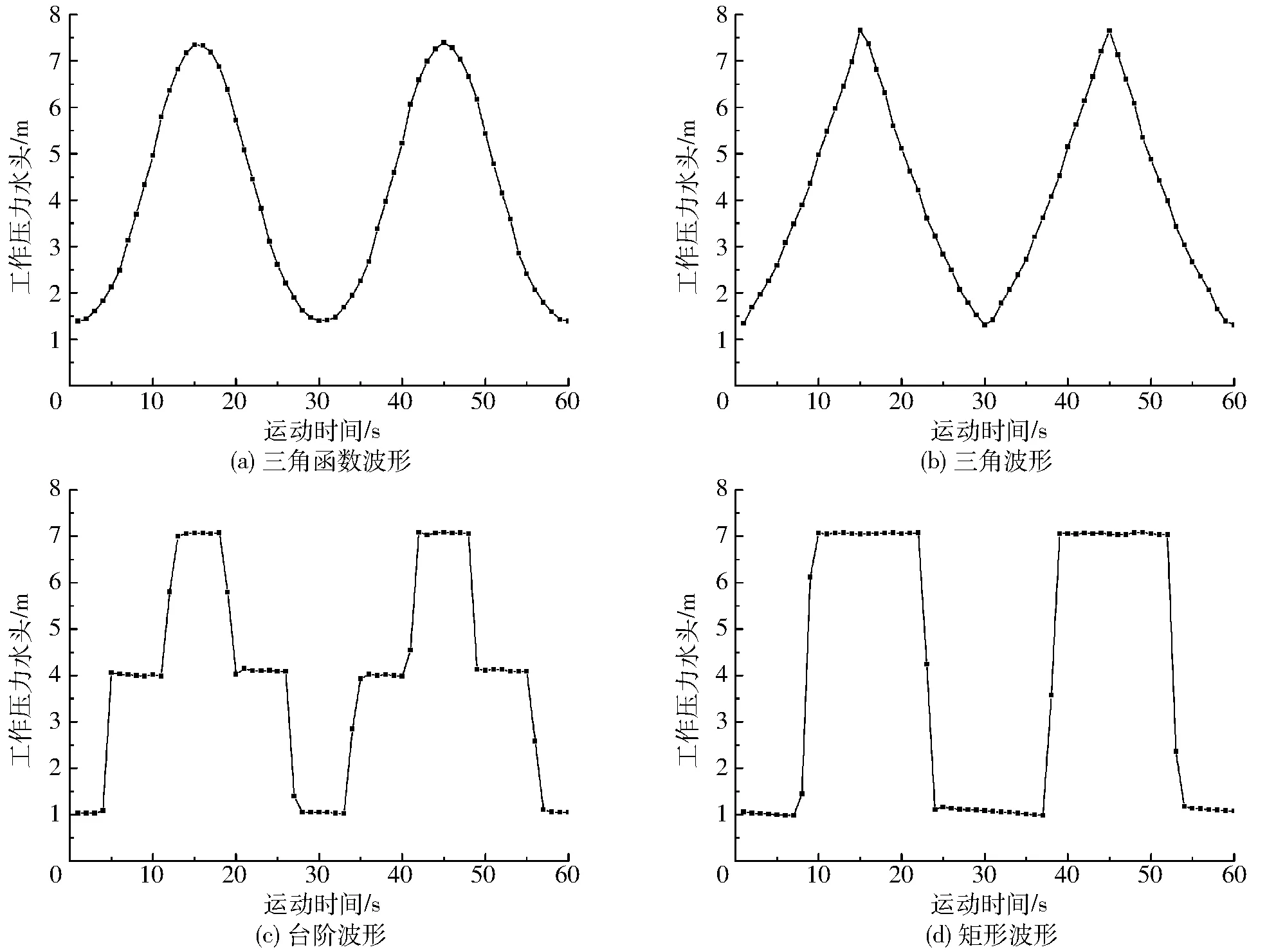
图4 动态水压模式示意图Fig.4 Schematic diagrams of different dynamic water pressure modes

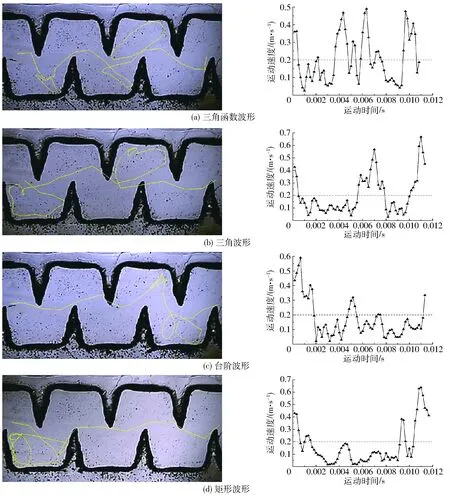
图5 不同动态水压模式下PTV观测颗粒物运动轨迹及瞬时运动速度Fig.5 Trajectory and velocity of PTV observation about particles under different dynamic water pressure modes

图5为不同动态水压模式下工作压力水头为4 m左右及颗粒运动时间均为0.012 s左右时PTV观测的第7和第8流道单元内单个颗粒物运动轨迹及瞬时运动速度。如图5所示，4种动态水压模式下颗粒物均进人了滞止区(流道可分为主流区和滞止区[19])，且颗粒物在滞止区的瞬时运动速度均较小，绝大部分在0.2 m/s(沙粒直径为10 μm左右时的止动比速[20])以下，说明4种动态水压模式下进入流道的颗粒物易随水流进入滞止区，滞止区水流流速较低，颗粒物长时间滞留滞止区易发生沉积。三角函数波形动态水压模式下颗粒物往返主流区和滞止区3次，平均每个流道单元内发生1次，且每次滞留滞止区的时间较短；三角及台阶波形动态水压模式下发生2次往返运动，且每次滞留在滞止区的时间较长；而矩形波形动态水压模式下仅发生1次往返运动，且每次滞留在滞止区的时间最长。由于三角函数波形动态水压模式下流道内水流流速始终保持大幅度地连续上下波动，水流紊动加剧，并产生强烈的水流波动效应，对滞止区水流不断发生冲击，滞止区与主流区水流和能量交换更为频繁，进入流道的颗粒物极易随水流进入滞止区，但在水流波动效应的作用下能迅速地返回主流区，并最终通过整个流道；三角波形动态水压模式下流道内工作水压的瞬时波动幅度低于三角函数波形动态水压模式下工作水压的瞬时波动幅度，其水流紊动强度及产生的水流波动效应相对较小，进入滞止区的颗粒物随水流不断运动，在水流波动效应的作用下返回主流区，并最终通过流道；台阶及矩形波形动态水压模式下流道内水流虽然流速波动也较大，但在波动期间较长时间流道内水流流速稳定在一定值，使得水流波动效应减弱，且对滞止区水流冲击的作用减弱，使得进入滞止区的颗粒物较长时间滞留在滞止区内，增大了颗粒物沉积的可能。

2.2 不同动态水压模式下颗粒物运动轨迹线

由于示踪粒子的布朗运动是由扩散引起的，单个颗粒物的运动情况存在较大的随机性，难以代表流场内所有颗粒物的运动规律，但所有颗粒物的布朗运动属于正态分布的随机运动，因此可以采用概率统计的方法，分析流场内所有颗粒物的运动规律[21]。本研究以颗粒物在流道流场内运动圈数作为统计指标，对大量颗粒物的运动轨迹进行统计分析，进而分析整个流道流场内颗粒物的运动情况。采用后处理软件Movias Pro Viewer 1.63对基础压力水头为4 m时不同动态水压模式下采集的颗粒物运动动态图像进行处理，分别从图像中随机选取300个进入滞止区的颗粒物，描绘每个粒子的运动轨迹线，并对颗粒物运动圈数按1、2、3、4、5(含5以上)5个水平进行统计。图6为不同动态水压模式下颗粒物运动圈数累积概率曲线。如图6所示，当颗粒物运动圈数为1时，三角函数波形动态水压模式下颗粒物运动圈数的累积概率最大，累积概率为35%；三角波形及台阶波形的次之，累积概率均为31%左右；矩形波形的最小，累积概率为29%左右；当颗粒物运动圈数为3时，三角函数波形动态水压模式下颗粒物运动圈数累积概率最大，累积概率为86%；三角波形及台阶波形的次之，累积概率分别为77.8%和77%；矩形波形的最小，累积概率为75.8%。当颗粒物运动圈数为3～5时，三角函数累积概率曲线斜率最为平缓，三角及台阶波形次之，矩形波形最大。由此可以看出，对于不同动态水压模式，粒子运动圈数从少到多的次序为：三角函数、三角、台阶、矩形波形，说明三角函数波形动态水压模式下水流对颗粒物的输移能力可能最大。

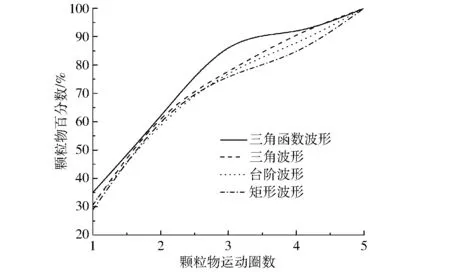
图6 不同动态水压模式下流道内颗粒物运动 圈数累积概率曲线Fig.6 Probability cumulative curves for particles circle number under dynamic water pressure modes

图7 不同运动圈数下颗粒物平均通过时间Fig.7 Histogram of particles average transit time in different particles circle numbers

图7为不同动态水压模式下颗粒物通过PTV观测区域的平均时间。由图7可知，随着颗粒物运动圈数的增加，4种动态水压模式下颗粒物平均通过时间均不断增大；不同运动圈数时，三角函数波形动态水压模式下颗粒物平均通过时间最短，三角及台阶波形动态水压模式下的次之，矩形波形动态水压模式下的最长。由此可以看出，对于不同动态水压模式，颗粒物平均通过时间从小到大的次序为：三角函数、三角、台阶、矩形波形。进一步说明三角函数波形动态水压模式下颗粒物在流道内停留时间最短，颗粒物在流道内的沉积概率最低，水流对颗粒物的输移能力最大。

2.3 迷宫流道滞止区局部流场分析

从上述4种动态水压模式下单个颗粒物运动情况的对比分析及多个颗粒物运动情况的统计分析可知，三角函数波形动态水压模式能最有效提高流道抗堵塞性能。为了进一步揭示三角函数波形动态水压模式下流道高抗堵塞性能的原因，对其流道内流场进行详细分析。

对于锯齿型迷宫流道，其齿尖后部流场较为复杂，且存在低速旋涡区，此处水流流速较小，甚至可能低于堵塞物质的起动速度，是流道中极易发生堵塞的区域[22-23]。因此，为了更加有效地分析迷宫流道流场细节，选取第7流道单元齿尖后部顶角局部区域作为流道流场分析的特征区域B(图8)。采用最近邻法对进入B区的颗粒物的运动情况进行匹配，获得B区颗粒物速度矢量图[24]，并分析进入B区近流道顶部0～0.1 mm处区域A(属于流道近壁区域，是颗粒物易于发生沉积的区域[5])内的颗粒物平均运动速度变化。

图8 PTV观测区域Fig.8 Schematic of PTV observation region

图10 迷宫流道顶角区域速度矢量图Fig.10 Velocity vectors of regional flow fields of micro-channels vertex angle

图9为三角函数波形动态水压模式下基础压力水头为4 m时一个完整周期T内近壁区内颗粒物平均运动速度变化曲线。随着时间变化，三角函数波形动态水压模式下流道内工作水压和近壁区内颗粒物的平均运动速度均呈先不断增大后不断减小的趋势，且其变化趋势基本一致；三角函数波形动态水压模式下近壁区内颗粒物的运动速度仍较低，但仍有一定程度的上下波动，从0.03 m/s左右不断增至0.159 m/s左右，而后不断下降至0.03 m/s左右。说明三角函数波形动态水压模式下近壁区水流受流道内水流波动效应的影响，水流紊动加剧，进入近壁区的颗粒物易随水流不断运动，降低了颗粒物沉积的可能，甚至部分颗粒物在水流波动效应的作用下能够迅速重返主流区，并最终通过流道。

图9 近壁区内颗粒物平均运动速度变化曲线Fig.9 Variation curves of particles average velocity in near-wall region

图10为三角函数波形动态水压模式下基础压力水头为4 m时一个完整周期T(进口水压先从Hmin变化至Hmax，再从Hmax变化至Hmin)内迷宫流道齿尖后部顶角区域速度矢量图。如图10所示，流道内工作水压波动初期，流道内工作压力水头最低，迷宫流道齿尖后部顶角区域存在较大的漩涡区，漩涡区水流流速及颗粒物运动速度均较低；随着时间的变化，流道内工作压力水头不断增大，迷宫流道齿尖后部顶角区域内低速漩涡区遭到冲击，在接近主流区的边缘位置颗粒物运动方向剧烈变化，并形成了为数较少的新的小漩涡；当工作压力水头增大到最大值时，迷宫流道齿尖后部顶角区域内低速漩涡区遭到强烈冲击，整个漩涡区内颗粒物运动方向变化更为剧烈，原有的漩涡结构遭到严重破坏，并形成了为数较多的新的小漩涡；随着时间的继续变化，流道内工作压力水头不断降低，迷宫流道齿尖后部顶角区域内遭到破坏的低速漩涡区逐渐恢复，仅在接近主流区的边缘位置仍然存在为数较少的小漩涡；当流道内工作压力水头降低至最低值时，迷宫流道齿尖后部顶角区域内遭到破坏的低速漩涡区已经完全恢复。由此可以看出，随着时间的变化，流道内工作压力水头不断发生变化，流道内水流紊动剧烈，形成的水流波动效应使得流道滞止区低速漩涡不断遭到冲击并发生破坏，而后又逐渐恢复；在流道工作水压较低时水流的波动效应使得进入滞止区的颗粒物随水流不断运动，不易在滞止区内产生沉积；在流道内工作压力水头较大时水流的波动效应使得进入滞止区的颗粒物能随水流迅速通过流道，并对滞留甚至沉积在滞止区内的颗粒物发生强烈冲击，使得颗粒物离底悬浮，返回主流区，并迅速通过流道，极大地增大了水流对颗粒物的输移能力，从而增强流道的抗堵塞性能。

3 结论

(1)对于不同动态水压模式，颗粒物运动圈数从少到多的次序为：三角函数、三角、台阶、矩形波形；颗粒物平均通过时间从小到大的次序为：三角函数、三角、台阶、矩形波形，说明三角函数波形动态水压模式下颗粒物在流道内停留时间最短，颗粒物在流道内的沉积概率最低，水流对颗粒物的输移能力最大。

(2)三角函数波形动态水压模式下流道内水流流速始终保持大幅度地连续上下波动，水流紊动加剧，并产生强烈的水流波动效应，不断冲击流道滞止区的水流，使得流道滞止区内的低速漩涡不断遭到冲击并发生破坏，而后又逐渐恢复；使得进入流道滞止区的颗粒物在流道工作压力水头较低时随水流不断运动，不易在流道内产生沉积，在流道内工作压力水头较大时能随水流迅速通过流道；使得滞留甚至沉积在滞止区内的颗粒物离底悬浮，返回主流区，并迅速通过流道，极大地增大了水流对颗粒物的输移能力，从而增强流道的抗堵塞性能。

1 HUANG S, DONG W, WEI Q, et al. Advanced methods to develop drip emitters with new channel types [J]. Applied Engineering in Agriculture, 2006, 22(2): 243-249.

2 TAYLOR H D, BASTORS R K X, PERSON H W, et al. Drip irrigation with waste stabilization pond effluents: solving the problem of emitter fouling[J]. Water Science Technology, 1995, 31(12): 417-424.

3 王文娥, 王福军, 严海军. 迷宫滴头CFD分析方法研究[J]. 农业机械学报, 2006, 37(10): 70-73. WANG Wen’e, WANG Fujun, YAN Haijun. Study on CFD method for flow simulation in labyrinth in the emitter[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(10): 70-73. (in Chinese)

4 李云开, 杨培岭, 任树梅, 等. 分形流道设计及几何参数对滴头水力性能的影响[J]. 机械工程学报, 2007, 43(7): 109-114. LI Yunkai, YANG Peiling, REN Shumei, et al. Effects of fractal flow path designing and its parameters on emitter hydraulic performance[J]. Chinese Journal of Mechanical Engineering, 2007, 43(7): 109-114. (in Chinese)

5 冯吉, 孙昊苏, 李云开. 滴灌灌水器内颗粒物运动特性的数字粒子图像测速[J]. 农业工程学报, 2013, 29(13): 90-97. FENG Ji, SUN Haosu, LI Yunkai. Visualizing particles movement characteristics in drip irrigation emitters with digital particle image velocimetry[J]. Transactions of the CSAE, 2013, 29(13): 90-97. (in Chinese)

6 魏正英, 赵万华, 唐一平, 等. 滴灌灌水器迷宫流道主航道抗堵设计方法研究[J]. 农业工程学报, 2005, 21(6): 1-7. WEI Zhengying, ZHAO Wanhua, TANG Yiping, et al. Anti-clogging design method for the labyrinth channels of drip irrigation emitters[J]. Transactions of the CSAE, 2005, 21(6): 1-7. (in Chinese)

7 芦刚, 史玉升, 魏青松, 等. 基于两相流模拟的高抗堵滴灌灌水器开发方法[J]. 华中科技大学学报：自然科学版, 2007, 35(7): 118-121. LU Gang, SHI Yusheng, WEI Qingsong, et al. A development method for high anti-clogged drip emitters based on two-phase flow simulations[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2007, 35(7): 118-121. (in Chinese)

8 喻黎明, 梅其勇. 迷宫流道灌水器抗堵塞设计与PIV试验[J/OL]. 农业机械学报, 2014, 45(9): 155-160. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20140926&flag=1.DOI:10.6041/j.issn.1000-1298.2014.09.026. YU Liming, MEI Qiyong. Anti-clogging design and experimental investigation of PIV for labyrinth-channel emitters of drip irrigation emitters[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(9): 155-160. (in Chinese)

9 喻黎明, 谭弘, 邹小艳,等. 基于CFD-DEM耦合的迷宫流道水沙运动数值模拟[J/OL]. 农业机械学报, 2016, 47(8): 65-71. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160810&flag=1. DOI: 10.6041/j.issn.1000-1298.2016.08.010. YU Liming, TAN Hong, ZOU Xiaoyan, et al. Numerical simulation of water and sediment flow in labyrinth channel based on coupled CFD-DEM[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(8): 65-71. (in Chinese)

10 ZHANG J, ZHAO W, TANG Y, et al. Structural optimization of labyrinth-channel emitters based on hydraulic and anti-clogging performance[J]. Irrigation Science, 2011, 29(5): 351-357.

11 魏正英, 唐一平, 温聚英, 等. 灌水器微细流道水沙两相流分析和微PIV及抗堵实验研究[J]. 农业工程学报, 2008, 24(6): 1-9． WEI Zhengying, TANG Yiping, WEN Juying, et al. Two-phase flow analysis and experimental investigation of micro-PIV and anti-clogging for micro-channels of emitter[J]. Transactions of the CSAE, 2008, 24(6): 1-9. (in Chinese)

12 牛文全, 吴普特, 喻黎明. 基于含沙量等值线的迷宫流道结构抗堵塞设计与模拟[J]. 农业工程学报, 2010, 26(5): 14-20. NIU Wenquan, WU Pute,YU Liming. Anti-clogging experimental investigation and optimized design of micro-channels of emitter based on isoline of sand content[J]. Transactions of the CSAE, 2010, 26(5): 14-20. (in Chinese)

13 ASSOULINE S, MOLLER M, COHEN S, et al. Soil-plant system response to pulsed drip irrigation and salinity[J]. Soil Science Society of America Journal, 2006, 70(5): 35-42．

14 ELMALOGLOU S, DIAMANTOPOULOS E. Wetting front advance patterns and water losses by deep percolation under the root zone as influenced by pulsed drip irrigation[J]. Agricultural Water Management, 2007, 90(1-2) : 160-163．

15 芦刚. 工作水压对滴灌灌水器水力性能影响规律的研究[D]. 武汉: 华中科技大学, 2010. LU Gang. Research on influence laws of the operating water pressure on hydraulic properties of drip emitters[D]. Wuhan: Huazhong University of Science and Technology, 2010. (in Chinese)

16 王聪. 波动水压对灌水器水力性能影响的实验研究[D]. 武汉: 华中科技大学, 2011. WANG Cong. Research on experiment of the effect of dynamic pressure on the hydraulic properties of drip Emitters[D]. Wuhan: Huazhong University of Science and Technology, 2011. (in Chinese)

17 刘洁, 王聪, 魏青松, 等. 波动水压参数对灌水器水力性能影响试验[J]. 河海大学学报: 自然科学版, 2014, 42(4): 361-366. LIU Jie, WANG Cong, WEI Qingsong, et al. Experimental study of effect of fluctuating water pressure factors on hydraulic properties of drip emitters[J]. Journal of Hohai University: Natural Sciences, 2014, 42(4): 361-366. (in Chinese)

18 GB/T 17187—2009 农业灌溉设备 滴头和滴灌管 技术规范和试验方法[S]. 2009.

19 郑超, 吴普特, 张林, 等. 动态水压下迷宫流道水流运动特性研究[J/OL]. 农业机械学报, 2015, 46(9): 167-172.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150924&flag=1.DOI:10.6041/j.issn.1000-1298.2015.09.024. ZHENG Chao, WU Pute, ZHANG Lin, et al. Flow characteristics in labyrinth channel under dynamic water pressure[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(9): 167-172. (in Chinese)

20 钱宁, 万兆惠. 泥沙运动力学[D]. 北京: 科学出版社，2003.

21 TAL S, ZUR B. Flow regime in helical long-path emitters[J]. Journal of the Irrigation & Drainage Division, 1980, 106(1): 27-35.

22 王文娥, 王福军, 严海军. 迷宫滴头CFD分析方法研究[J]. 农业机械学报, 2006, 37(10): 70-73. WANG Wen’e, WANG Fujun, YAN Haijun. Study on CFD method for flow simulation in labyrinth emitter[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(10): 70-73. (in Chinese)

23 金文, 张鸿雁. 灌水器内流道流场Micro-PIV试验分析[J]. 农业工程学报, 2010, 26(2): 12-17. JIN Wen, ZHANG Hongyan. Micro-PIV analysis of flow fields in flow channel of emitter[J]. Transactions of the CSAE, 2010, 26(2): 12-17. (in Chinese)

24 禹明忠. PTV技术和颗粒三维运动规律的研究[D]. 北京: 清华大学, 2002. YU Mingzhong. Study on the PTV technique and 3D movement of particles[D]. Beijing: Tsinghua University, 2002. (in Chinese)

Particles Movement Characteristics in Labyrinth Channel under Different Dynamic Water Pressure Modes

ZHENG Chao1WU Pute1,2ZHANG Lin1,2ZHU Delan2ZHAO Xiao2AN Boda2

(1.InstituteofSoilandWaterConservation,NorthwestA&FUniversity,Yangling,Shaanxi712100,China2.InstituteofWater-savingAgricultureinAridAreasofChina,NorthwestA&FUniversity,Yangling,Shaanxi712100,China)

The movements of tracer particles in a labyrinth channel were observed by using the PIV technique. The pressure was in dynamic modes with trigonometric function, triangular, step and rectangular waveforms. The trajectories, velocity of single particle as well as the overall flow field in the channel were analyzed to reveal the anti-clogging mechanism of dynamic water pressure. The results showed that when compared with constant water pressure, flow rates in the channel under trigonometric function, triangular, step and rectangular waveforms dynamic pressure modes were not decreased significantly. Therefore, effect of dynamic water pressure on water delivery capacity of drip irrigation system was not obvious. Among the different dynamic water pressure modes mentioned above, the trigonometric function type demonstrated the shortest particles residence time in the flow stagnation region. The deposition probability of particles was the lowest under this mode, indicating a better particles transport capacity in the channel. Fluctuation effect generated by the water under pressure of trigonometric function form produced effect on the low-speed swirl in the stagnation region, and aggravated the turbulence of flow in this region. The turbulent flow was enhanced and the ability to carry the particles retained or even deposited in the stagnation zone was improved. As a result, the particles were suspended from the bottom and returned back to the main flow path. The transport capacity of the flow got strengthened, and the anti-clogging performance of the channel was improved.Therefore, the trigonometric function waveform dynamic water pressure model can most effectively improve the anti-clogging performance in the labyrinth channel.

dynamic water pressure; labyrinth channel; particles; velocity; trajectory

10.6041/j.issn.1000-1298.2017.03.037

2016-11-08

2016-12-28

中国科学院西部之光人才培养计划项目、西北农林科技大学基本科研业务费专项资金项目(2014YB061)和“十二五”国家科技支撑计划项目(2015BAD22B01-02)

郑超(1989—)，男，博士生，主要从事节水灌溉理论研究，E-mail： zhengchao_xinong@163.com

吴普特(1963—)，男，研究员，博士生导师，主要从事水资源高效利用研究，E-mail： gizwpt@vip.sina.com

S275.6

A

1000-1298(2017)03-0294-08