雷达组网协同探测试验航次数量设计改进

刘　钦

(中国电子科技集团公司第二十研究所　西安　710068)

0　引言

在雷达组网中，多部雷达波束指向同一区域同时探测同一目标是一种有效的协同探测方式，可以增加对目标的稳定跟踪距离、提早建立目标航迹、扩大武器的有效使用范围，提高雷达传感器抗干扰能力和航迹连续性。

目标的雷达横截面积(Radar Cross Section，RCS)是随视角变化而起伏的[1]。在先前的研究中[2]，我们发现不同雷达在同一时刻观测到起伏目标的RCS的相关性未知，不满足传统的“或”准则检测融合使用条件。因此，我们根据不同雷达探测起伏目标截面积间的相关程度和分布式检测融合算法计算获得了一种新的雷达组网协同探测范围计算方法。

为了充分验证该算法的正确性，需要在实际的外场环境下，利用实装飞机作为目标，测试两部同型雷达对目标协同探测的稳定跟踪距离。由文献易知，航次数越多，样本量越多，统计结果越接近于真实值，但经济成本也越高。为了降低航次数，可增大距离取样间隔，但传统航次数计算方法将距离取样间隔内检测概率的变化视为线性变化，当距离取样间隔增加时，数据评估的检测概率与实际雷达检测概率间出现明显误差，使得统计结果的可靠性下降。基于此，本文提出一种航次数修正算法，通过对融合检测概率进行多项式拟合与积分，消除传统航次数计算方法的误差，获得准确的航次数，并选择最佳的距离取样间隔。

1　协同探测试验航次数计算方法

某一高度所需检飞航次按照如下公式计算

(1)

其中，ΔR为距离取样间隔，单位为km；无特殊要求时，距离取样间隔按以下规定选取：a)垂直波束宽度大于2°的中、远程雷达，距离取样间隔ΔR一般为20km；b)近程雷达及垂直波束宽度小于2°的中、远程雷达，ΔR一般为10km；c)当需观测受检雷达垂直波瓣分裂情况时，距离取样间隔ΔR一般为10km。N为距离取样间隔内所需观测点数；根据检飞所要求的置信水平和置信区间[3,4]，可按下图确定所需观测点数。

V是目标机相对雷达速度，单位为km/h；T为观测周期，单位为s。

试验雷达的发现概率为0.8，观测周期为3s。设置置信水平为0.95，当要求统计结果以95%的概率落入置信区间0.75～0.84内时，则距离取样间隔内所需观测点数N=300，如图1所示；当要求统计结果以95%的概率落入置信区间0.71～0.875内时，距离取样间隔内所需观测点数N=100，按照目标速度为75m/s计算航次数如下表所示。

表1不同距离取样间隔下所需航次数

距离取样间隔发现概率的置信区间采样点数所需航次数5km0．75～0．840300140．71～0．875100510km0．75～0．84030070．71～0．875100315km0．75～0．84030050．71～0．875100220km0．75～0．84030040．71～0．8751002

由上述计算结果可以看出，距离取样间隔越大，所需航次数越少。但是，式(1)将同一距离取样间隔内检测概率的变化视为线性，当距离取样间隔变大时，这种近似算法将会出现较大误差，因此，必须对检测概率的误差进行补偿。

2　协同探测检测概率函数拟合

N部相同雷达采用“或”准则对目标的总检测概率为

(2)

(3)

(b)假设当N部相同雷达同时探测目标，目标对于不同雷达呈现出完全不相关(独立)的起伏特性，式(2)可以化简为

(4)

由式(3)和式(4)可以计算获得离散的两部雷达的联合检测概率，如图2所示，接下来还需进行多项式拟合。对于一组给定的数据{(dt,pdt),t=1,…,T}，其中dt为t时刻目标与雷达距离，pdt为雷达对dt距离目标的检测概率，利用多项式拟合融合检测概率。

多项式拟合的数学模型[5]为

y(x)=f(a,x)=a1xn+a2xn-2+…+anx+an+1

3　协同探测航次数计算改进

从表1的航次计算结果可以看出，当置信区间大小相同时，距离取样间隔越大所需航次数越小。但是，增大距离取样间隔将会增加数据评估时统计误差。采用传统数据评估方法，距离取样间隔中心的检测概率=距离取样间隔内发现点数/应有点数。这种统计方法将距离取样间隔内检测概率的变化视为线性变化，当距离取样间隔增大时，数据评估的检测概率与实际雷达检测概率间出现明显误差，如图3所示。

表2不同距离取样间隔下统计误差

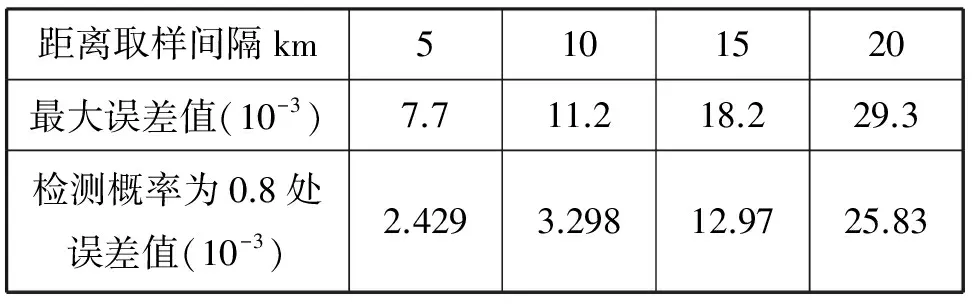
距离取样间隔km5101520最大误差值(10-3)7．711．218．229．3检测概率为0．8处误差值(10-3)2．4293．29812．9725．83

考虑不同距离取样间隔下统计误差对置信区间的影响，不能直接通过图1查得观测点数，采用如下公式重新计算距离取样间隔内所需观测点数。

(5)

NΔR为观测点数，P为检测概率，δ是置信区间长度的一半，Δδ为统计误差，Kα/2是置信限。然后将得到的所需观测点迹数代入式(1)即可获得较为准确的航次数。

4　仿真计算

仿真中假设对于σav=1m2，R=45km的目标，当Pf=10-6时，Pd=0.8；目标起伏服从Swerling I型统计模型。目标速度为270km/h，观测周期为3s，距离取样间隔分别设置为5km、10km、15km、20km。

假设对统计结果的置信度为1-α=95%，置信区间长度为0.1，Kα/2=1.96，计算结果如下表所示。

表3不同距离取样间隔下航次数

距离取样间隔等效置信区间长度试验所需观测点数单航次点数航次数5km0．09512722212．222510km0．0934282446．3408

续表

根据上表所述，从经济角度出发应选择距离取样间隔为10km，需要约7个航次。

当置信度为1-α=90%，置信区间长度为0.1，Kα/2=1.645。考虑统计误差，目标速度270km/h，计算所得航次数如下表所示。

表4不同距离取样间隔下航次数(置信度为0.90)

距离取样间隔等效置信区间长度试验所需观测点数单航次点数航次数5km0．0951192228．609510km0．0934199444．466515km0．0741316674．736320km0．0483742898．3378

根据上表所述，从经济角度出发应选择距离取样间隔为10km，需要约5个航次。

根据上述分析结果，推荐设置置信度为90%，距离取样间隔为10km，数据评估需要5个航次，考虑到正式试验前需对雷达的发现距离和跟踪距离进行实测，还需对ADS-B接收信号的连续性进行测试，需再增加2～3个航次，则每次试验需7个航次。

5　结束语

协同探测试验的航次数与距离采样间隔取值

相关，从经济角度出发，距离取样间隔越大，所需有效航次数越少。但是距离取样间隔增大，将引起统计结果误差增大。本文提出一种航次数修正算法，准确估计了试验结果统计误差，并对试验所需观测点数进行修正，获得了合理的航次数，对实际多雷达协同探测试验具有较高的指导意义。

参考文献:

[1]Skolnik M I.雷达系统导论(第三版)[M]. 北京: 电子工业出版社，2012.

[2]胡小全, 刘钦, 孙建军. 雷达组网协同探测范围研究[J]. 雷达科学与技术, 2015, 13(3): 223-227.

[3]郝继平, 李军, 李昕泽. 目标探测精度试验的样本和航次数量设计及其应用[J]. 中北大学学报(自然科学版), 2008, 29(4): 380-384.

[4]杨琳, 朱元昌, 邸彦强等. 雷达动态精度试验误差统计分析方法改进[J]. 测控技术, 2014, 33(9): 48-55.

[5]李健翩, 李学仁. 多项式拟合在试飞数据预处理中的应用[J]. 弹箭与制导学报, 2005, 25(4): 799-801.